Unfolding of Ubiquitin Studied by Picosecond Time-Resolved Fluorescence of the Tyrosine Residue

Abstract

The photophysics of the single tyrosine in bovine ubiquitin (UBQ) was studied by picosecond time-resolved fluorescence spectroscopy, as a function of pH and along thermal and chemical unfolding, with the following results: First, at room temperature (25°C) and below pH 1.5, native UBQ shows single-exponential decays. From pH 2 to 7, triple-exponential decays were observed and the three decay times were attributed to the presence of tyrosine, a tyrosine-carboxylate hydrogen-bonded complex, and excited-state tyrosinate. Second, at pH 1.5, the water-exposed tyrosine of either thermally or chemically unfolded UBQ decays as a sum of two exponentials. The double-exponential decays were interpreted and analyzed in terms of excited-state intramolecular electron transfer from the phenol to the amide moiety, occurring in one of the three rotamers of tyrosine in UBQ. The values of the rate constants indicate the presence of different unfolded states and an increase in the mobility of the tyrosine residue during unfolding. Finally, from the pre-exponential coefficients of the fluorescence decays, the unfolding equilibrium constants (K_U) were calculated, as a function of temperature or denaturant concentration. Despite the presence of different unfolded states, both thermal and chemical unfolding data of UBQ could be fitted to a two-state model. The thermodynamic parameters T_m = 54.6°C, ΔH^Tm = 56.5 kcal/mol, and ΔC_p = 890 cal/mol//K, were determined from the unfolding equilibrium constants calculated accordingly, and compared to values obtained by differential scanning calorimetry also under the assumption of a two-state transition, T_m = 57.0°C, ΔH_m= 51.4 kcal/mol, and ΔC_p = 730 cal/mol//K.

INTRODUCTION

Kinetic studies of protein unfolding are generally carried out using optical methods, such as absorption or fluorescence spectroscopy (Fersht, 1999). These studies require previous characterization of the optical properties of the protein, and determination of the unfolding equilibrium constants K_U and thermodynamic parameters (Cantor and Schimmel, 1980; Robertson and Murphy, 1997). Time-resolved fluorescence spectroscopy (TRFS) was recently applied to determine the K_U values of a single-tryptophan protein (Staphylococcus aureus nuclease A) as a function of temperature (Faria et al., 2004). This was accomplished by identification of the native (N) and the unfolded (U) protein decays, followed by determination of the molar fractions of N and U from the pre-exponential coefficients of the decays. The method allowed direct determination of K_U values from the molar fractions, and indirect determination of thermodynamic parameters from van't Hoff plots of K_U.

Early attempts of the application of TRFS to proteins with a single tyrosine, such as histone H1 (Libertini and Small, 1985), Cu,Zn superoxide dismutase (Ferreira et al., 1994), and transcriptor factor 1 (Härd et al., 1989), have shown that the tyrosine decays are multiexponential in nature. In fact, model compounds of tyrosine in water show, on their own, double-exponential decays (Laws et al., 1986). As a result of the complex decays and low fluorescence quantum yield, the use of tyrosines as internal probes, capable of tracking conformational changes in proteins, has been hindered. For example, in the case of ubiquitin (UBQ), another protein with a single tyrosine, kinetic studies by fluorescence spectroscopy have so far only been carried out on a tryptophan variant of the protein (F45W) (Khorasanizadeh et al., 1993; Krantz and Sosnick, 2000).

In a recent study (Noronha et al., 2004), we have shown that observation of multiple decay times with N-acetyl-L-tyrosinamide (NAYA), an adequate model compound of a tyrosine within a protein, is rather the exception than the rule and depends on solvent polarity and temperature. Shortly, low polarity and high temperature causes a change from double- to single-exponential on the decays of NAYA. The detailed interpretation of these photophysical properties (Noronha et al., 2004), improved the possibility of understanding the nature of complex decays for a tyrosine residue in a protein.

In this work, we explore the possibility of studying the folding kinetics of the wild-type UBQ, using the fluorescence of its tyrosine residue. Specifically, the photophysical characterization of the protein is first carried out, and the tyrosine decays are then employed for direct evaluation of K_U and thermodynamic data.

Ubiquitin was chosen because it is a small protein, of 76 amino acid residues (8.5 kDa), found in all eukaryotic cells, whose sequence is well conserved from protozoan to vertebrates. It has a single tyrosine located within the protein, no tryptophans, no cysteine residues, or disulphide bridges. Furthermore, its three-dimensional structure has been determined by x-ray crystallography (Vijay-Kumar et al., 1987) and nuclear magnetic resonance (NMR) (Cornilescu et al., 1998). Fluorescence of the tyrosine in UBQ was shown to be susceptible to quenching due to the presence of a carboxylate group of a nearby aspartic or glutamic amino acid (Jenson et al., 1980). On examination of UBQ's structure, it is not clear whether it is the aspartic (Asp-58) or the glutamic acid (Glu-51) that is responsible for the fluorescence quenching. Nevertheless, the tyrosine-carboxylate interaction was also observed by NMR, in an independent study, by observing the change in the chemical shift of tyrosine as a function of pH from 1 to 13 (Cary et al., 1980). Finally, unfolding of UBQ has been thoroughly studied by different biophysical techniques (Ibarra-Molero et al., 1999; Colley et al., 2000) and by varying denaturing conditions.

EXPERIMENTAL

N-acetyl-L-tyrosinamide (NAYA) was purchased from Sigma Chemical (Sintra, Portugal) and used as such after verification of purity by high-performance liquid chromatography. Bovine ubiquitin (UBQ) was also purchased from Sigma Chemical and purified on a MONO-S column using a salt gradient (NaCl 1 M) as described by Ferreira and Shaw (1989). Fractions of 1 ml were collected and further dialyzed against 12.5 mM sodium acetate, pH 4.5 at 4°C and adjusted to a final protein concentration of 1 mg/ml. Their purity was verified not only by SDS-PAGE (which showed a single band in a 12% acrylamide gel) but also by careful inspection of the absorption and fluorescence spectra. The final test of purity was carried out using time-resolved fluorescence, with the criterion of observing single-exponential decays of the samples at pH 1.5, independently of excitation or emission wavelengths. The samples were excited at λ_exc = 275 nm and λ_exc = 284 nm and collected at λ_em = 295 nm and λ_em = 320 nm (4-nm bandwidth). Protein concentration was determined using an extinction coefficient of 1254 dm³ mol⁻¹ cm⁻¹ at 280 nm (0.149 ml¹ mg⁻¹ cm⁻¹ and a molecular weight of 8433 Da) (Ibarra-Molero et al., 1999). Guanidine hydrochloride (GuHCl) was of ultrapure grade (>99.5%) and purchased from Sigma. Sodium acetate (Merck, Lisbon, Portugal), sodium chloride (Merck), acetic acid (Riedel-deHaën, Lisbon, Portugal) and hydrochloric acid (Riedel-deHaën) were of pro analysis grade. 1,4-dioxane (Riedel-deHaën) of spectroscopic grade was distilled over sodium to remove excess water and a residual impurity.

Ultra-violet absorption spectra were measured using an Olis-15 double-beam spectrophotometer with 1.0-nm resolution. Steady-state fluorescence excitation and emission spectra were measured using a SPEX Fluorog 212I spectrofluorimeter (SPEX, Lisbon, Portugal). All spectra were collected in the S/R mode and corrected for optics, detector wavelength dependence (emission spectra), and lamp intensity wavelength dependence (excitation spectra). Fluorescence was collected at right-angle geometry. The fluorescence quantum yields of UBQ were determined by comparison with the quantum yield of NAYA in dioxane (Noronha et al., 2004), which was in turn determined by comparison to a standard solution of p-terphenyl in cyclohexane (0.77) (Murov et al., 1993) and corrected for the differences in refractive indexes.

Time-resolved fluorescence measurements were carried out using the single-photon counting technique as previously described (Giestas et al., 2003). Excitation of samples was carried out with the frequency-tripled output of an actively mode-locked picosecond Ti-Sapphire laser (Tsunami, Spectra Physics, Lisbon, Portugal), pumped by a solid-state laser (Millennia Xs, Spectra Physics). The repetition rate was set to 4 MHz by passage through an optical-acoustic modulator (Pulse Selector 3980, Spectra Physics). Excitation was vertically polarized and emission was collected at the magic angle of 54.7°. Inverted START-STOP configuration was used in the acquisition. The experimental instrumental response function for all excitation wavelengths was in the 38–42-ps range. Alternate collection of pulse profile and sample decays was performed (10³ counts at the maximum per cycle), until ∼5 × 10³ detected counts at the maximum of the fluorescence signal. Fluorescence decays measured until 1 × 10⁴ counts gave identical results. Unless otherwise mentioned, the fluorescence decay measurements were carried out using a 24.26 ps/ch timescale. The fluorescence decays were deconvoluted in a PC, using George Striker's program (LINUX version; Striker et al., 1999).

Differential scanning calorimetry (DSC) measurements were carried out on a VP-DSC microcalorimeter from Microcal (Lisbon, Portugal) equipped with 0.51 mL cells and controlled by the VP-Viewer program. Calibration of temperature and heat flow was carried out according to the MicroCal instructions. The samples of protein concentration 1 mg/ml were extensively dialyzed using a Spectra/Por membrane with a molecular weight cutoff of 3500 Da at 4°C against the buffer and further degassed before the calorimetric experiments. The samples were heated from 10 to 100°C at a scan rate of 1°C/min and the calorimetric cells were kept under an excess pressure of 28 psi during the scan to avoid bubble formation during the experiments. Thermal unfolding of UBQ was carried out in 10 mM glycine-HCl at pH 2, pH 1.5, and in 12.5 mM sodium acetate-HCl at pH 1.5. The thermograms were analyzed using the DSC support software provided by MicroCal, using as model a two-state transition with ΔC_p.

RESULTS

The effect of pH on the fluorescence of UBQ

The absorption spectrum of bovine ubiquitin (UBQ) at pH 4.5 (Fig. 1 a) shows a maximum at λ = 277 nm with well-defined peaks corresponding to the 0–0 (284 nm) and 0–1 (277 nm) vibrational transitions of its single tyrosine as seen for the parent compound NAYA (Scheme 1) in the nonpolar solvent dioxane (Noronha et al., 2004). In addition, the presence of four other vibrational transitions in the region from 240 to 250 nm are also observed, which are attributed to the presence of two phenylalanines in UBQ. On acidification to pH 1.5, no change in the absorption spectrum was observed (data not shown).

FIGURE 1.

(a) Absorption spectrum of bovine UBQ at pH 4.5 in 12.5 mM sodium acetate at 25°C shows a maximum absorption at λ = 277 nm and four peaks in the 250–260-nm range attributed to the presence of two phenylalanines. Fluorescence spectrum at pH 4.5 shows reduced quantum yield of φ_F = 0.046 and an increase to φ_F = 0.20 at pH 1.5 with no significant red shift. (b) Normalized fluorescence spectrum of ubiquitin at pH 4.5 (solid circles), pH 1.5 (open circles), and pH 11 (open triangles). The normalized difference between the normalized spectra at pH 4.5 and pH 1.5 (solid triangles) is identical to the spectrum measured at pH 11.

SCHEME 1.

Molecular structure of NAYA.

The fluorescence quantum yield of UBQ at pH 4.5 (φ_F = 0.046) is almost fourfold lower than quantum yield of NAYA in dioxane (φ_F = 0.18), which is believed to be due to quenching by a carboxylate group in the nearby vicinity of the tyrosine residue (Jenson et al., 1980). Acidification from pH 4.5 to pH 1.5 results in an increase in fluorescence quantum yield, from φ_F = 0.046 at pH 4.5 to φ_F = 0.20 at pH 1.5 (Fig. 1 a). (The emission spectra of UBQ at pH 1.5 and pH 4.5 were normalized at 290 nm to avoid interferences, which may appear as a result of the presence of complexes at longer wavelengths.) Subtraction of the normalized spectrum of UBQ at pH 1.5 from the spectrum at pH 4.5 showed the appearance of a second emission band, which is identical to the normalized emission spectrum of UBQ at pH 11 (Fig. 1 b). The excitation spectrum of UBQ at pH 4.5, measured at 295 and 350 nm show identical spectrum (data not shown), which indicates that tyrosine absorption is responsible for the emission at both wavelengths.

Additionally, the fluorescence intensity of UBQ measured in D₂O, pH 8.7 is ∼20% greater than in H₂O at pH 7. Normalization of the fluorescence spectra in D₂O at pH 8.7 and in H₂O at pH 7 also shows a lesser contribution from the emission band at 350 nm in D₂O. On acidification to pH 1.5, a fourfold increase in the fluorescence intensity is observed in D₂O and H₂O and normalization show identical spectra in D₂O and H₂O at pH 1.5. The two observations are in agreement with the existence of a hydrogen-bonded complex between tyrosine to a nearby carboxylate group or quenching due to a proton transfer mechanism.

Emission bands in the wavelength range (330–350 nm) have been assigned to tyrosinate, formed in the excited state by proton transfer from tyrosine to a proton acceptor (Shimizu et al., 1979; Alev-Behmoaras et al., 1979) or to a hydrogen-bond tyrosine complex (Willis and Szabo, 1991). However, to date, direct experimental evidence demonstrating the occurrence of excited-state proton transfer from tyrosine in proteins has not been presented (Ross et al., 1992).

Fig. 2 a shows a fluorescence decay of UBQ carried out at pH 1.5 and at 25°C, with excitation at λ_exc = 275 nm and emission at λ_em = 295 nm. The decay is strictly single-exponential with lifetime equal to τ₁ = 3.84 ns. Fluorescence decays collected at λ_em = 320 nm are also adjustable with single-exponential functions with an identical decay time. The result shows that single-exponential decays are possible for a protein with a single tyrosine, in the absence of other perturbations.

FIGURE 2.

(a) Single-exponential fluorescence decay of UBQ in sodium acetate 12.5 mM HCl (pH 1.5), at 25°C (λ_exc = 275 nm, λ_em = 295 nm). (b) Global analysis of decays of UBQ in sodium acetate 12.5 mM, at pH 4.5 and 25°C, measured with excitation at λ_ext = 275 nm and emission at λ_em = 295 nm and λ_em = 350 nm, require sums of three exponentials. At 350 nm, the decay shows a rise-time, which indicates the presence of a species that is formed in the excited state.

Increasing the pH to 4.5 (Fig. 2 b) and further to pH 7 induces a gradual appearance of two additional decay times (τ₂ ∼650 ps and τ₃ ∼190 ps at pH 7.0), whereas the normalized pre-exponential coefficient of the longest decay time A₁ (τ₁ = 1.52 ns at pH 7.0) decreases from 1.0 (at pH 1.5) to 0.06 (at pH 7). Plots of fluorescence decay times and their corresponding pre-exponential coefficients, as a function of pH, are shown in Fig. 3.

FIGURE 3.

(a) Decay times (τ₁, τ₂, and τ₃) dependence on pH of UBQ in 12.5 mM sodium acetate HCl at 25°C. (b) Normalized pre-exponential coefficients A₁, A₂, and A₃ as a function of pH, showing the predominance of A₁ at pH 1.5 and that of A₂ and A₃ at pH 7.0.

The presence of excited-state tyrosinate in UBQ at pH 4.5

Fig. 2 b shows a global analysis of two fluorescence decays of UBQ at pH 4.5, measured with excitation at 275 nm and emission at λ_em = 295 and λ_em = 350 nm. The decay at 350 nm shows a rise-time (negative pre-exponential factor) of the shortest decay time, τ₃. Independent analysis of both the decays at 295 nm and 350 nm also required sums of three exponential functions, with decay times and pre-exponential coefficients similar to those obtained from the global analysis. The observation of a rise-time means that the emission at 350 nm has the contribution of a species that is absent in the ground state and is formed during the lifetime of the excited tyrosine. The values of the pre-exponential coefficients at 350 nm, after subtraction of the tyrosine contribution to the emission at 350 nm and normalization are A₃ = −0.508, A₂ = 0.898, and A₁ = 0.102. (At 350 nm and pH = 4.5, both tyrosine and some other X species emit, the relative contributions of each being equal to and . The steady-state intensities are in turn related to the pre-exponential coefficients and decay times by and . 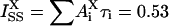The pre-exponentials of tyrosine alone were obtained from the decay measured at 295 nm; intensity normalized to 0.47. These were then subtracted from the pre-exponential coefficients of the decay measured at 350 nm 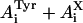; intensity normalized to 0.53, thus yielding the values of .) The sum of pre-exponentials, after correction, is not equal to zero (ΣA_i = 0.49), suggesting the presence of a third species present in the ground state at pH 4.5, which is absent at pH 1.5 at 350 nm in UBQ. Hydrogen-bond complexes of tyrosine with acetate have been reported to emit in the 310–345-nm wavelength region (Willis and Szabo, 1991).

Fluorescence decays of UBQ at pH 11, measured at 350 nm with a 24.26 ps/ch timescale, are double exponentials with decay times equal to 63 ps (A₂ = 0.89) and 345 ps (A₁ = 0.11). We observed for the model parent compound, NAYA in water at pH 11, a double-exponential decay with decay-time values of 4.8 ps (A₂ = 0.60) and 39 ps (A₁ = 0.40). Although the pre-exponential coefficients are similar, the major contribution to the fluorescence is associated to the 39 ps decay time, which is close to the lifetime of the anion of tyrosine in water (26 ps) at pH 11 as observed by Willis and Szabo (1991). However, in the case of NAYA anion in dioxane/water mixtures, an increase in the decay time with increasing dioxane content (i.e., decreasing dielectric constant) to 73 ps (30:70 dioxane/water) and 89 ps (60:40 dioxane/water) was observed. As mentioned above, the tyrosine residue within UBQ is located in a less polar environment than pure water, which may explain the major decay time of UBQ (63 ps) at pH 11.

Heat denaturation of ubiquitin followed by TRFS

The thermal unfolding of UBQ was studied at pH 1.5 and 4.5. At pH 4.5, the pattern of fluorescence decays as a function of temperature is complex and will not be treated in this article.

At pH 1.5, the absorption spectrum showed a shift of 0.5 nm to the blue with increasing temperature from 25°C to 70°C, and no significant change in the extinction coefficient. Fluorescence emission spectra showed first a gradual reduction in the quantum yield from φ_F = 0.20 at 25°C to φ_F = 0.16 at 46°C and then a sharper decrease to φ_F = 0.036 at 70°C.

The fluorescence decays of UBQ at pH 1.5 are single exponentials up to 42.4°C. In the temperature range from 44.4°C to 72.4°C (where unfolding occurs), two additional shorter decay times were observed. The decay times and pre-exponential coefficients are shown in Fig. 4. In Fig. 4 a, the temperature dependence of the fluorescence lifetimes of the model compound NAYA, in dioxane/water mixtures is also presented.

FIGURE 4.

(a) Lifetimes of NAYA in dioxane/water mixtures (dioxane, 20% H₂O, 40% H₂O, 60% H₂O, 80% H₂O, and Water), as a function of temperature, are presented in solid circles. The long decay time of UBQ, τ₁, follows the 40% H₂O profile, whereas τ₂ andτ₃ appear at 44.4°C and follow a profile similar to the major and minor decay times of NAYA in water. (b) The normalized pre-exponential coefficient A₁ decreases from 1 at 27.4°C to 0.02 at 72.4°C, whereas pre-exponential coefficients A₂ and A₃ vary from 0 at 27.4°C to 0.68 and 0.30, respectively, at 72.4°C.

The temperature dependence of τ₁ (Fig. 4 a) follows the profile of the lifetime of NAYA in a 60% dioxane/water mixture. The second and third decay times (τ₂ and τ₃) are comparable to the major and minor decay times of NAYA in water, respectively (Noronha et al., 2004).

The pre-exponential coefficient A₁ (Fig. 4 b), which corresponds to τ₁, gradually tends to 0 for temperatures above 70°C, whereas the pre-exponential coefficients of τ₂ and τ₃ (A₂ and A₃) increase with temperature up to A₂ = 0.68 and A₃ = 0.31 at 73°C (Fig. 4 b).

In summary, the foregoing results indicate that the fluorescence of native UBQ (T < 44.4°C) is described by a single-exponential decay with a long decay time (τ₁), whereas the unfolded UBQ (T > 70°C) is responsible for the short double-exponential decay (τ₂ and τ₃).

Chemical denaturation of ubiquitin followed by TRFS

The absorption spectra of chemically denatured ubiquitin at pH 1.5 and 25°C showed a blue shift of 1.0 nm from 277 nm to 276 nm and a reduction in fluorescence quantum yield from φ_F = 0.20 at 0 M to φ_F = 0.10 at 4.5 M GuHCl (data not shown).

The time-resolved fluorescence decays are fitted with single exponentials from 0 to 1 M GuHCl, double exponentials at 2 M GuHCl, and triple-exponential functions from 3 to 4.5 M GuHCl. The longest lifetime τ₁ increases from 3.84 ns at 0 M to 4.1 ns at 4.5 M GuHCl. The middle decay time τ₂ = 1.32 ns is constant from 3 to 4.5 M and the third decay time increases from τ₃ = 172 ps at 2 M to 395 ps at 4.5 M GuHCl (Fig. 5 a).

FIGURE 5.

(a) Fluorescence decay times τ₁, τ₂, and τ₃ of UBQ at pH 1.5 as a function of increasing GuHCl concentration at 25°C. (b) The normalized pre-exponential coefficient A₁ decreases from 1 at 0 M GuHCl to 0.10 at 4.5 M GuHCl and A₂ and A₃ increase with increasing concentrations of GuHCl.

The pre-exponential coefficient A₁ decreases from 1.0 at 0 M GuHCl to 0.10 at 4.5 M GuHCl, whereas the pre-exponential coefficients A₂ and A₃ increase up to 0.50 and 0.40, respectively, at 4.5 M GuHCl (Fig. 5 b). Therefore, also here the fluorescence of native UBQ is described by the long decay time, and the unfolded UBQ is described by two shorter decay times.

In addition, denatured UBQ at pH 1.5 and 4.5 M GuHCl was measured with excitation at λ_ext = 275 nm and at four different emission wavelengths (295, 310, 320, and 330 nm). The time-resolved decay-associated spectra of all decay times (τ₁, τ₂, and τ₃) were similar to the steady-state emission spectrum of UBQ, indicating that the decay times are unlikely to be attributed to an impurity.

Thermal unfolding of UBQ studied by DSC

The DSC thermograms of UBQ in 10 mM glycine HCl at pH 2, pH 1.5, and in 12.5 mM sodium acetate HCl at pH 1.5 were analyzed on the basis of the two-state model (Wintrode et al., 1994) and good fits were observed (Fig. 6). Analysis with non-two-state models did not improve the fits. The thermodynamic parameters derived from the two-state analysis are presented in Table 1. Our results show good agreement for T_m and with the values cited in literature for UBQ in 10 mM glycine buffer at pH 2 as previously determined by Wintrode et al. (1994) (T_m = 57°C, ΔH_cal = 46.8 kcal/mol, ΔH_vH = 49.7 kcal/mol, and ΔC_p = 1.1 kcal/mol/°C). The parameters derived from the DSC experiments in glycine pH 1.5 and sodium acetate pH 1.5 show an increase of 1.6 and 2.1°C in the transition temperature and an increase of 2.9 and 2.7 kcal/mol in enthalpy when compared to the values determined in glycine at pH 2. This increase is interpreted on the basis of a stabilizing effect observed in presence of chloride anions (∼31 mM in HCl pH 1.5) (Makhatadze et al., 1998).

FIGURE 6.

(a) DSC thermogram of UBQ in glycine 10 mM at pH 2 from 30 to 80°C (solid circles) analyzed using the two-state model with ΔC_p (line). (b) Thermogram of UBQ in sodium acetate 12.5 mM at pH 1.5 from 30 to 85°C (solid circles) analyzed using the two-state model with ΔC_p (line).

TABLE 1.

Mean values (average of five independent DSC measurements) of unfolding transition temperature (T_m), enthalpy (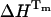), and heat capacity at constant pressure (ΔC_p) of ubiquitin in 10 mM glycine at pH 2, pH 1.5, and in sodium acetate HCl 12.5 mM, at pH 1.5, obtained by DSC using the “Two-State with ΔC_p” model provided in the MicroCal software

Buffer	pH	Tm(°C)	(kcal/mol)	ΔCp(kcal/mol/K)
Glycine	2.0	54.9 ± 0.7	48.7 ± 1.4	0.78 ± 0.12
Glycine	1.5	56.5 ± 0.5	51.6 ± 1.0	0.70 ± 0.10
Acetate	1.5	57.0 ± 0.6	51.4 ± 1.8	0.73 ± 0.28

DISCUSSION

The pH effect on the fluorescence of UBQ

The effect of pH on the steady-state fluorescence of UBQ was previously studied by Jenson et al. (1980) and Ibarra-Molero et al. (1999). It was observed that the fluorescence intensity of UBQ displays a sigmoidal increase on acidification from pH 4.5 to pH 1.5 with the half-value of the maximum fluorescence intensity I_1/2 at pH = 3.9 (Jenson et al., 1980). We have made similar observations with I_1/2 at pH = 3.5. Jenson and co-workers attributed the fluorescence quenching of the single tyrosine of UBQ, at higher pH values, to the presence of a nearby carboxylate group of an aspartic (pK_a ∼4.0 in water) or glutamic (pK_a ∼4.5 in water) amino acid, which is protonated in this pH range. Further evidence for the tyrosine-carboxylate interaction has also been detected by NMR (Cary et al., 1980).

The pH titration data obtained by TRFS shows that the tyrosine residue in UBQ decays as a single exponential only below pH 1.5. Above pH 1.5, triple-exponential decay functions were required (Fig. 3). In addition, a second emission band with maximum at 350 nm, identical to the fluorescence emission of tyrosinate of UBQ at pH 11 (Fig. 1 b), and displaying an excitation spectrum identical to the absorption spectrum of tyrosine, is observed. The detection of a rise-time at 350 nm demonstrates that the species emitting at this wavelength is formed in the excited state (Fig. 2 b). Therefore, we assign this emission to the tyrosinate ion formed after excited-state proton transfer from the phenol to the carboxylate group of the nearby ionized aspartic or glutamic acid.

The foregoing results strongly support that excited-state proton transfer (ESPT) from the phenol to carboxylate groups may occur in proteins, and that it is the mechanism responsible for the quenching of tyrosine fluorescence in UBQ. The presence of the three decay times at pH 4.5 indicates the existence of three different excited-state species, from which two (which are associated to τ₂ and τ₃) disappear on protonation of the nearby carboxylate group. The remaining long decay time, τ₁ = 3.84 ns below pH 3.8, is similar to the lifetime of NAYA in a mixture of 60% dioxane/water (τ₀ = 3.84 ns at 25°C), and its pre-exponential coefficient decreases to values close to 0 at pH values above 5, where the deprotonation of aspartic and glutamic acids is complete (Fig. 3 b). Therefore, τ₁ is attributed to tyrosine in the absence of proton-transfer quenching, in the protonated protein.

Within the 2–7 pH range, UBQ may exist in two “states” with respect to the ionization of the carboxylic group (ionized and non-ionized). Hence, a tyrosine can be either in the presence of a side-chain carboxylic acid (non-ionized state) or a side-chain carboxylate group (ionized state). When in the presence of the protonated side-chain carboxylic acid (RCOOH), single-exponential decays are expected with a decay time equal to the long decay time τ₁ = 3.84 ns, if the carboxylic group remains protonated during the lifetime of tyrosine. (In fact, the pK_a values of aspartic acid, pK_a ∼4.0, or glutamic acid, pK_a ∼4.5, indicate that deprotonation of these acids should be slower than 10⁷ s⁻¹—assuming diffusion-controlled protonation of the conjugate base, ∼10¹⁰ M⁻¹ s⁻¹.)

On the other hand, tyrosines in protein states, in which the carboxylate group is ionized (RCOO⁻), are expected to demonstrate double-exponential decays, with a rise-time at 350 nm, if tyrosinate is formed in the excited state after proton transfer from tyrosine to the RCOO⁻ group. The decay times (τ₂ and τ₃) are, under these conditions, functions of the four rate constants of the excited-state processes involved in the quenched tyrosine-tyrosinate equilibrium. If we further account for the possibility of interconversion of the two protein “states” (protonated and deprotonated) during tyrosine lifetime (i.e., deprotonation of the nearby carboxylic acid), the three decay times will also be functions of the protonation and deprotonation rates of the carboxylate and carboxylic groups, respectively. Consequently, τ₂ and τ₃ do not have direct physical meaning, but the shortest time τ₃ ≈ 70 ps at pH 3 (λ_em = 295 nm) seems dominated by the fast decay of the tyrosinate ion [τ₀ (UBQ, tyrosinate) = 63 ps at pH 11 or τ₀ (NAYA, tyrosinate) = 89 ps in 60:40 dioxane/water, pH 11].

Our attempts at detecting a rise-time for the tyrosine model compound (NAYA) in the presence of 0.5 M acetate at pH 6 were unsuccessful despite the observation of a second emission band with maximum at 340 nm. The intensity at 340 nm seemed insufficient to allow splitting of the decaying and rising fast components of the overlapping emissions. Identical results were obtained by Willis and Szabo (1991) using tyrosine in the presence of acetate and other proton acceptors. The observation of the rise-time in the case of UBQ is believed to be possible only because of the existence of a tyrosine-carboxylate complex present in the ground state, which is substantiated by the fact that the sum of the pre-exponential coefficients at 350 nm is not equal to 0 (see Results).

Summarizing, UBQ appears to be the first case study for a tyrosine within a protein where the formation of tyrosinate in the excited state by an ESPT mechanism can be observed.

Nature of double-exponential decays of unfolded UBQ

As mentioned above (see Results), the fluorescence decay of the water-exposed tyrosine in unfolded UBQ at pH 1.5 is described by two exponentials. We observed double-exponential decays for the model compound of tyrosine NAYA in water, which are due to excited-state intramolecular electron transfer from the phenol to the amide moiety, occurring in one of the three rotamers of NAYA (Noronha et al., 2004). Double-exponential decays observed for tryptophan model compounds or in proteins have also been attributed to a photo-induced electron transfer process (Chen and Barkley, 1998; Hudson et al., 1999). Observation of double-exponential decays depends on three factors:

1. The molar fractions of ground-state rotamer population, where the rotamer conformations are defined at the C_α–C_β bond (α).

2. The rotational rate constants between the rotamers, k_r and 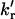(the value k_r refers to the formation of the quenched conformer, where the phenol group is closest to the carbonyl group of the amide moiety, which is required for efficient electron transfer; 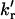refers to the reverse process).

3. The photo-induced electron transfer rate constant, k_ET.

On application of the model (Noronha et al., 2004) to the data obtained for UBQ in the temperature range from 57 to 72.4°C, the following observations were made. First, on normalization of the pre-exponential coefficients of the unfolded protein decay, A₂ and A₃, to 1, values close to A₂ = 0.60 and A₃ = 0.40 were observed in the temperature range from 57 to 72.4°C (Fig. 7). These values are greater than those observed for NAYA (Noronha et al., 2004), but similar to those observed by Laws and co-workers for dipeptides (tyrosylglycine and glycyltyrosine) (Laws et al., 1986; Ross et al., 1986). From the decay times and pre-exponential coefficients of unfolded UBQ (Fig. 7), values of the rotational rate constants (k_r and 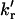), electron-transfer rate constant k_ET, and molar fraction of the quenched tyrosine rotamer α = k_r/(k_r + 2 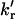) in UBQ were calculated using the proposed model. Arrhenius plots of the rate constants are shown in Fig. 8 and values of the quenched rotamer and rate constants at three temperatures are compared to those obtained for NAYA in Table 2. The values in Table 2 show that, except for the clearly lower values of 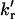in UBQ, all other rate constants are similar to those of NAYA. This strongly indicates that the double-exponential nature of the exposed tyrosine in unfolded UBQ is also due to intramolecular electron transfer.

FIGURE 7.

(a) Pre-exponential coefficients of the water-exposed tyrosine in UBQ, A₂, and A₃, normalized to 1, show a decrease in A₃ from 0.94 at 44.4°C to 0.31 at 72.4°C and an increase in A₂ from 0.06 at 44.4°C to 0.69 at 72.4°C. (b) A₂ and A₃ determined from the unfolding of UBQ at pH 1.5 with GuHCl show a similar profile as observed in the case of unfolding with temperature, where A₃ is predominant at low denaturing concentration and decreases to 0.44 at 4.5 M GuHCl, whereas A₂ increases gradually from 0 at 1 M GuHCl to 0.56 at 4.5 M GuHCl.

FIGURE 8.

Arrhenius plots of the rotational rate constants k_r and 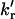and the electron-transfer rate constant (k_ET) of the water-exposed tyrosine residue in unfolded UBQ. The plots show clear deviation from linearity in the temperature range from 44.4 to 57°C for k_r and .

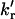TABLE 2.

Comparison of the ground-state population of the quenched rotamer (α), rate constants of rotamers exchange (k_r and 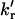), and the intramolecular electron transfer rate constant (k_ET) at 50, 60, and 70°C of NAYA in water and ubiquitin in 12.5 mM sodium acetate HCl at pH 1.5

	NAYA*			UBQ
	50°C	60°C	70°C	50°C	60°C	70°C
α	0.29	0.28	0.28	0.75	0.61	0.59
kr/ns−1	0.89	1.1	1.4	0.75	0.99	1.32
	1.1	1.4	1.8	0.12	0.32	0.46
kET/ns−1	2.9	3.3	3.6	3.2	3.3	3.8

^*Noronha et al., 2004.

Below 57°C, the normalized pre-exponential coefficient of the unfolded UBQ decay related to τ₃ is predominant (A₃ = 0.94 at 44.4°C) and gradually tends to 0.33 at 70°C (Fig. 7). Furthermore, the Arrhenius plots in Fig. 8 show clear deviation from linearity in the temperature range from 44.4 to 57°C. This observation suggests that at the early stages of protein unfolding, the tyrosine residue retains a conformation favoring the electron transfer process, where the phenol ring is in close proximity to the carbonyl group of the tyrosine peptide backbone. At higher temperatures, the rotational rate constants increase, allowing for the appearance of other conformations, and as a result, an increase in the pre-exponential coefficient of τ₂ is observed (from A₂ = 0.06 at 44.4°C to 0.66 at 70°C). These results indicate that unfolded UBQ defined at 44.4°C is different from the unfolded UBQ at 70°C, in terms of tyrosine rotamer populations.

The chemical denaturation of UBQ with GuHCl shows a pattern similar to that seen in the case of thermal unfolding. The pre-exponential coefficient A₃ is predominant at low concentrations of GuHCl and decreases to A₃ = 0.44 at 4.5 M GuHCl, whereas A₂ is absent below 2 M GuHCl and increases up to A₂ = 0.56 at 4.5 M GuHCl (Fig. 7 b).

Determination of UBQ unfolding equilibrium constants (K_U) from TRFS data

The unfolding of UBQ was carried out at pH 1.5 to avoid complications in the determination of native and unfolded concentrations of UBQ, which would arise at higher pH values, where the native UBQ is described by three decay times. On the basis of the assignments of the decay times (see Results, above), the fluorescence intensity at t = 0 of the native UBQ (pH 1.5) is described by Eq. 1, where A₁ is the pre-exponential coefficient of the longest exponential term, after normalization, :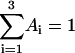

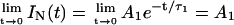(1)

.Upon unfolding (above 42°C or above 1 M GuHCl at 25°C), two additional decay times (τ₂ andτ₃) were observed, which are similar to the decay times of NAYA in water when the expectable difference in rotamer interconversion rates in NAYA and UBQ is taken into account. The fluorescence intensity at t = 0 of unfolded UBQ is, therefore, given by the sum of the normalized pre-exponential coefficients A₂ + A₃, which varies from 0 to 1 (Eq. 2):

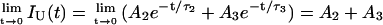(2)

.The pre-exponential coefficient of the native (A₁) or unfolded UBQ (A₂+A₃) is, in turn, related to the concentration at t = 0 of the corresponding excited species, ([N*](0) or [U*](0)), times the radiative rate constant of each species 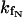or , assuming that the protein folding and unfolding rate constants are slow in comparison to the reciprocal decay times of N* and U* (Faria et al., 2004). The experimental fluorescence intensities of native, and unfolded, 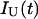protein conformations are furthermore dependent on the fraction of light that is detected at the experimental emission wavelength 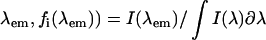, of each species i = N or U, with respect to the total fluorescence emission, 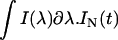and 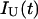are related to the excited-state concentrations ([N*](0) or [U*](0)) by Eqs. 3 and 4, respectively, where c₂ and c₃ define the relative weights of the two exponential terms of the water-exposed tyrosine fluorescence decay in the unfolded protein conformation (Faria et al., 2004):

(3)

,

(4)

.For the determination of [N*](0) and [U*](0), the pre-exponential coefficients must be first divided by 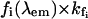and then normalized such that [N*](0) + [U*](0) = 1.

In the case of the model compound of tyrosine NAYA, a small bathochromic shift of 2 nm in the emission spectrum from dioxane to water was observed. The same observation was also made with UBQ, where the normalized spectrum of native UBQ (at 25°C) showed a 2-nm shift with respect to the normalized spectrum of unfolded UBQ (at 72°C) (data not shown). As a result, the normalized spectra are almost coincident, i.e., f_N(λ_em) ≈ f_U(λ_em) for UBQ, at 305 nm.

The radiative rate constant of NAYA (k_f) does not change from dioxane (3.5 × 10⁷ s⁻¹) to water (3.6 × 10⁷ s⁻¹), within experimental error. Therefore, on the basis that NAYA is an acceptable model compound, .

The ground-state concentration of native or unfolded UBQ is proportional to the concentration of each excited species at t = 0 multiplied by its molar extinction coefficient (ɛ_i) at the excitation wavelength. In the case of UBQ, no significant change in the extinction coefficient was observed as a function of temperature. This was also observed in case of unfolding carried out at 25°C with GuHCl (only a 2% difference was observed between ɛ_native and ɛ_denatured) (data not shown).

Summarizing, as a result of no significant change in the fraction of light at the emission wavelength (f_i(λ_em)), radiative rate constants () and molar extinction coefficients (ɛ_i) between the native and unfolded UBQ, the normalized pre-exponential coefficient A₁ is equal to the ground-state molar fraction of the folded UBQ (x_N) and the sum A₂ + A₃ is equal to the ground-state molar fraction of the unfolded UBQ (x_U).

Therefore, under the assumption of a two-state mechanism, direct determination of unfolding equilibrium constants (K_U) of UBQ along thermal unfolding was carried out from the pre-exponential coefficients shown in Fig. 4 b (Eq. 5):

(5)

.

Chemical denaturation of UBQ

From the pre-exponential coefficients of the decays as a function of increasing denaturant concentration (Fig. 5 b), the equilibrium constants (K_U) of chemical unfolding were likewise calculated using Eq. 5.

The plot of the Gibbs energy (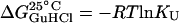) as a function of GuHCl concentration (not shown) is linear (R² = 0.99), according to Eq. 6, where 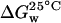is the Gibbs energy in water (absence of denaturant) (Schellman, 1978),

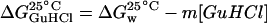(6)

.From this plot, values of the change in Gibbs energy with denaturant concentration, m = 1.67 kcal/mol/M (7.0 kJ/mol/M) and , at 25°C, were obtained, in agreement with values reported in literature (m = 8.0 kJ/mol/M and ).

Thermodynamic analysis of TRFS data

Information on the thermodynamics of thermal unfolding of UBQ can also be obtained from the unfolding equilibrium constants (K_U) at each temperature. The equilibrium constant is related to Gibbs energy (), which is, in turn, related to the unfolding enthalpy at the melting temperature T_m by the modified Gibbs-Helmholtz equation (Eq. 7), where ΔC_p represents the change in the specific heat capacity during unfolding at constant pressure:

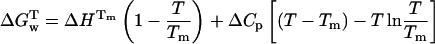(7)

.Rearrangement of Eq. 7 as a function of the unfolding equilibrium constant results in a nonlinear function (Eq. 8) from which the values of T_m, 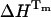, and ΔC_p associated to UBQ unfolding is determined:

(8)

.Fig. 9 a shows the fit of Eq. 8 to our equilibrium data with the following values: T_m = 54.6 ± 0.5°C, 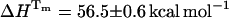, and . Interestingly, when we attempted to fit Eq. 8, imposing a , a good fit was also observed in the region of T_m with small deviations only at the higher and lower temperatures (Fig. 9 b). Moreover, the thermodynamic parameters calculated from Fig. 9 b, T_m = 54.3 ± 0.5°C, 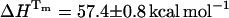are practically identical to the values calculated assuming a . This results from the cancellation of the 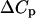terms in Eq. 8 at T = T_m, and at temperatures close to the denaturation temperature. Then, if ΔC_p is not too large, as in the present case, its influence on the obtained 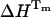value at the transition temperature will be small. This illustrates that knowledge of 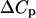is not required for the evaluation of 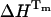and 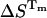from the equilibrium constants measured at temperatures close to T_m.

FIGURE 9.

Van't Hoff plot of the unfolding equilibrium constants K_U of UBQ in 12.5 mM sodium acetate HCl, pH 1.5 determined by TRFS: (a) fit of Eq. 8, from which the transition temperature (T_m), enthalpy (), and heat capacity at constant pressure (ΔC_p) are calculated and (b) linear regression, imposing ΔC_p = 0.

If we compare the thermodynamic parameters obtained by TRFS and DSC, a lower T_m = 54.6°C was determined by TRFS as compared to DSC (T_m = 57.0°C), showing a deviation of 2.4°C and a difference of 5.1 kcal/mol in the enthalpies (, 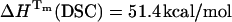) (Table 3), under the assumption that the unfolding is a two-state process. In a recent International Union of Pure and Applied Chemistry technical report on the measurement and analysis of thermal unfolding of lysozyme determined solely by DSC in different laboratories, the T_m values varied from 56.25 to 58.75°C and the enthalpy values spanned the range 90.1–104.9 kcal/mol (Hinz and Schwarz, 2001). The discrepancy in the enthalpy values of UBQ calculated from TRFS and DSC might then be considered within the experimental “between-sample” variation. However, we carried out five independent DSC runs of UBQ in sodium acetate HCl at pH 1.5 and five independent DSC runs in glycine HCl at pH 2 and observed a difference of no more than ±0.7°C in the T_m and ±1.8 kcal/mol in the enthalpy 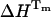(not shown).

TABLE 3.

Comparison of the unfolding transition temperature (T_m), enthalpy (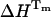), entropy (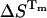), and heat capacity at constant pressure (ΔC_p) determined by time-resolved fluorescence spectroscopy (TRFS) and differential scanning calorimetry (DSC) of UBQ in sodium acetate HCl 12.5 mM, at pH 1.5

	Tm(°C)	ΔHm(kcal/mol)	ΔSm(kcal/mol/K)	ΔCp(kcal/mol/K)
TRFS*	54.3 ± 0.5	57.4 ± 0.8	0.175 ± 0.001	—
TRFS†	54.6 ± 0.5	56.5 ± 0.6	—	0.89 ± 0.13
DSC	57.0 ± 0.6	51.4 ± 1.8	—	0.73 ± 0.28

^*Values determined by linear regression.

^†Values obtained from the fit of Eq. 8.

If the discrepancy of 2.4°C and 5.1 kcal/mol observed in the T_m and enthalpy determined by TRFS and DSC has physical significance, it would imply that the region surrounding the tyrosine residue unfolds differently from the protein as a whole. Actually, in a recent study using time-resolved infrared spectroscopy (TRIRS), Colley et al. (2000) detected a T_m of 65°C for a reversible melting process of UBQ at pH 1, associated with loss of β-sheets structure, by monitoring the change in the integrated intensity at 1629 cm⁻¹. In view of these results, it is tempting to hypothesize the presence of regions within UBQ with different degrees of stability, placing the tyrosine in a region of the protein (located between an α-helix and a β-sheet), which is less stable than the regions corresponding to the β-sheets as observed from TRIRS.

Despite these observations, independent analysis of our data obtained by TRFS or DSC is consistent with a two-state model. This implies that, if hypothetically different transitions (corresponding to regions of different stability within UBQ) do occur, they must have sufficiently close 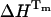and T_m values, so that they are experimentally undetectable by DSC or TRFS individually.

CONCLUSIONS

Photophysical characterization of tyrosine in UBQ

We have firstly shown that single-exponential fluorescence decays are possible for proteins with a single tyrosine, in the absence of other perturbations, as in native UBQ at pH 1.5. Second, ESPT and H-bond complex formation involving nearby ionized carboxylate-side-chain amino acids in the protein (Asp or Glu) was demonstrated to occur in native UBQ at higher pH values, leading to triple-exponential decays. Third, the water-exposed tyrosine in denatured UBQ undergoes excited-state electron transfer from the phenol to the backbone carbonyl group, thus decaying as sums of two exponentials.

Application of TRFS to track UBQ conformational changes

Unfolding equilibrium constants, K_U, can be accurately calculated from molar fractions of the native and unfolded protein, derived from the pre-exponential coefficients of the respective tyrosine decays. Successful application of TRFS to tyrosine residues opens the door to the possibility of characterizing the unfolding kinetics of wild-type UBQ.

TRFS also provided direct experimental evidence for the existence of a continuum of different unfolded states, referent to the region surrounding the tyrosine residue in UBQ. Different techniques, such as TRIRS, may access different regions of this continuum, whereas DSC reports on the continuum as a whole.

Summarizing, picosecond TRFS is shown to possess advantages over the conventional use of steady-state fluorescence, such as the detection of impurities, interactions of tyrosine with nearby amino acids, and the presence of different unfolded states. In future, we plan to apply TRFS to more complex situations such as UBQ at pH 4.5 and to proteins with multiple tyrosine residues.