An All-Atom Force Field for Tertiary Structure Prediction of Helical Proteins

Abstract

We have developed an all-atom free-energy force field (PFF01) for protein tertiary structure prediction. PFF01 is based on physical interactions and was parameterized using experimental structures of a family of proteins believed to span a wide variety of possible folds. It contains empirical, although sequence-independent terms for hydrogen bonding. Its solvent-accessible surface area solvent model was first fit to transfer energies of small peptides. The parameters of the solvent model were then further optimized to stabilize the native structure of a single protein, the autonomously folding villin headpiece, against competing low-energy decoys. Here we validate the force field for five nonhomologous helical proteins with 20–60 amino acids. For each protein, decoys with 2–3 Å backbone root mean-square deviation and correct experimental C_β–C_β distance constraints emerge as those with the lowest energy.

INTRODUCTION

Ab initio protein tertiary structure prediction (PSP) remains among the most important outstanding problems of biophysical chemistry (Baker and Sali, 2001; Moult et al., 2001; Schonbrunn et al., 2002). The many complementary proposals for PSP span a wide range of representations (Go and Scheraga, 1976; Nemethy et al., 1992; Ulrich et al., 1997; Zhou and Karplus, 1999; Simons et al., 1997, 1999; Pillardy et al., 2001; Liwo et al., 2002; Nanias et al., 2003) of the protein conformation, ranging from coarse-grained models to atomic resolution. The choice of representation often correlates with the methodology employed in structure prediction, ranging from empirical potentials for coarse-grained models (Go and Scheraga, 1976; Ulrich et al., 1997; Nanias et al., 2003) to complex atom-based potentials that directly approximate the physical interactions in the system (Duan and Kollman, 1998; Snow et al., 2002). The latter offer insights into the mechanism of protein structure formation and promise better transferability (Vasquez et al., 1994), but their use incurs large computational costs that has confined all-atom protein structure prediction to small peptides (Snow et al., 2002; Simmerling et al., 2002; Schug et al., 2003) and proteins (Hansmann, 2004; Herges and Wenzel, 2004; Schug et al., 2004). Recent evaluations of different approaches to PSP found that empirical, homology-based methods outperform the ab initio methods (Lattman, 2001; Bonneau et al., 2001), but that there is still much room for improvement in the quality of the predictions of all methods.

It has been one of the central paradigms of protein folding that proteins in their native conformation are in thermodynamic equilibrium with their environment (Anfinsen, 1973). Exploiting this characteristic the structure of the protein can be predicted by locating the global minimum of its free-energy surface (Liwo et al., 2002; Schug et al., 2003; Onuchic et al., 1997) without recourse to the folding dynamics (Vila et al., 2004; Herges and Wenzel, 2004). This approach is potentially much more efficient than the direct simulation of the folding process. Simulation by molecular dynamics elucidates the folding dynamics of the protein explicitly (Garcia and Onuchic, 2003) but strains presently available computational resources and will remain inapplicable to large proteins in the foreseeable future. For many questions regarding only the folded structure of the protein, PSP based on global optimization of a free-energy model may offer a viable alternative approach, provided that a suitable parameterization of the free energy of the protein in its environment exists and that the global optimum of this free-energy surface can be found with sufficient accuracy (Li and Scheraga, 1987).

PSP by optimization requires an accurate, yet tractable model for the low-energy portion of the free-energy surface of the protein and efficient optimization techniques which can reliably determine its global minimum. Despite a steady increase in available computational power, PSP remains one of the grand computational challenges, which constrains the choice of free-energy parameterizations. The free-energy model must describe the internal energy of the system and the entropy of both the molecule and the surrounding solvent. The major contribution to entropy differences among metastable configurations with long lifetimes and to the native conformation stems from changes in the free energy of the solvent and possibly the side chains. Changes in the solvent free energy may be approximated by simple implicit models based on the solvent-accessible surface area of the individual atoms (Eisenberg and McLachlan, 1986). Such terms also approximately account for the changes in the side-chain entropy upon burial and other nonbonded interactions with fictitious solvent molecules.

Here we investigate a strategy for all-atom protein structure prediction (Schug et al., 2003; Herges and Wenzel, 2004) in a minimal thermodynamic approach for a number of helical proteins. We report the rational development of an all-atom free-energy force field for proteins (PFF01), which is primarily based on physical interactions with important empirical, though sequence-independent, corrections. This force field was rationally optimized to stabilize the native conformations of the autonomously folding headpiece of the villin protein (PDB code 1VII), which was previously investigated in all-atom simulations using the AMBER (Duan and Kollman, 1998) and ECEPP/2 (Hansmann, 2002) force fields. We already demonstrated the reproducible and predictive folding of two proteins, the structurally conserved 40-amino-acid headpiece of the HIV accessory protein (1F4I) (Herges and Wenzel, 2004) and the 20-amino-acid Trp-cage protein (1L2Y) (Schug et al., 2003) with PFF01. Here we argue that PFF01 stabilizes the native conformations of three other proteins: the 53-amino-acid headpiece of protein A (Snow et al., 2002; Gouda et al., 1992) (Residues: 1–53) folds into a three-helix bundle and has been investigated using empirical and all-atom potentials (Zhou and Karplus, 1999; Shea et al., 1999; Vila et al., 2004). The engrailed homeodomain (1ENH) from Drosophila melanogaster (Clarke et al., 1994) is a prototypical α-helical protein that was recently investigated with respect to its folding stability and pathway in both simulation and protein-engineering experiments (Mayor et al., 2003). The bacterial ribosomal protein L20 (1GYZ) is a recently investigated 60-amino-acid protein (Raibaud et al., 2002), one of the smallest to fold into a stable four-helix bundle. We find for each of the proteins that a near-native conformation emerges as lowest in energy when compared to independently generated low-energy decoys. PFF01 thus emerges as a promising free-energy force field to explore techniques for all-atom protein structure prediction for a family of helical proteins. The decoys that were generated in this study may be used to validate force fields other than PFF01 for protein structure prediction.

METHODS

Free-energy model

Due to the complexity of protein interactions, force-field design must balance the quality of the representation and the computational demands of its evaluation (Vajda et al., 1997). PFF01 represents all atoms individually (with the exception of hydrogen in CH_n groups). During the folding process we consider only variations of the dihedral angles {θ_i} of the backbone and the side chains, while keeping all other angles and bond-lengths fixed. The energy is parameterized as

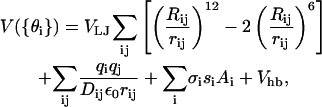(1)

using established, physically motivated contributions with an emphasis on the simplicity of their numerical evaluation. Here r_ij denotes the distance between atoms i and j, q_i the partial charge on atom i. A_i designates the surface of atom i that is exposed to a fictitious solvent. The latter is calculated as the area of a sphere with radius R_i (from the potential type associated with the atom) that is accessible to fictitious solvent molecules with a radius of 1.4 Å.

The atoms of the peptide are classified into potential-types according to their chemical characteristics as described in Table 1 (Avbelj and Moult, 1995a). The partial charges q_i and screening constants D_ij were taken from an adapted version (J. Moult, 1999, Electrostatic parameters for proteins; private communication) of an established electrostatic parameterization for proteins (Avbelj and Moult, 1995b). The Lennard-Jones radii (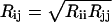) were derived in a potential-of-mean-force approach by fitting the experimentally observed short-range (2–5 Å) radial distributions of a set of 138 proteins that are believed to span a wide range of possible folds (Abagyan and Totrov, 1994). The final set of radii (see Table 2) reduced the number of clashes in native conformations by 99% in comparison to a Lennard-Jones parameterization taken from the OPLS force field (Jorgensen and McDonald, 1998) using a uniform value of V_LJ = 10 cal/mol.

TABLE 1.

Potential types of the side-chain atoms for each amino acid starting from the C_β atom outwards (top) and for the main chain and its termini

Amino acid	Potential type
ALA	CME
VAL	3 × CME
ILE	4 × CME
LEU	4 × CME
PHE	CME, 6 × CR
PRO	3 × CME
MET	CME, CME, S, CME
ASP	CME, CP, O2, O2
GLU	CME, CME, CP, O2, O2
LYS	3 × CME, CP, N3, 3 × H
ARG	3 × CME, N1, H, CP, 2 × (N1, H, H)
SER	CP, O1, H
THR	CP, CME, O1, H
TYR	CME, 6 × CR, O1, H
HIS	CME, CR, N1, H, CR, CR, N1, H
CYS	CME, S
ASN	CME, CP, O2, N2, H, H
GLN	CME, CME, CP, O2, N2, H, H
TRP	CME, 3 × CR, N1, H, 5 × CR
Main chain	N1, HM, CME, CP, O1
N-terminus	N3, H, H, H, CME, CP, O1
C-terminus	N1, HM, CME, CP, O1, O2

The first letter designates the atom; suffixes differentiate potential types in their chemical environment. CME is the potential type for united-atom CH_n groups; CR occurs in rings.

TABLE 2.

Lennard-Jones radii and solvation enthalpies [cal mol⁻¹ Å⁻²] for the potential types in PFF01

Potential type	Rii
CME	4.10	45	84
CP	4.10	39	−6
CR	3.28	63	93
N1	3.55	−60	−30
N2	3.55	−60	15
N3	3.55	−120	−45
O1	3.10	−30	−30
O2	3.10	−60	15
S	3.80	30	84
H	1.95	–	–
HM	2.25	–	–

All explicitly represent hydrogens carry the same solvation enthalpy as the heavy atom to which they are covalently bound. designate values of the solvation parameters before and after force-field optimization.

A model for main-chain hydrogen bonding, which governs secondary structure formation, must incorporate both electrostatic effects originating from the dipole-dipole interactions, as well as the alignment of the hydrogen mediating the bond with respect to the donor and acceptor groups (Sippl et al., 1984). To model the latter we have developed a corrective term,

(2)

where 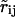is the distance between H and O of the amino and carboxyl groups, ν_ij is the NHO angle, and δ the angle between the CO and NH dipoles. The distributions of these parameters for the main-chain hydrogen bonds extracted from experimental protein structures are shown in Fig. 1. The radial dependence is modeled according to R(r) = s_{2.4, 0.075}(r), where Fig. 1 c indicates an additional correlation between the angles ν and δ, which is included in the angle-dependent term as

(3)

FIGURE 1.

(Top left) Definitions of the angles used to define the potential of mean force for main-chain hydrogen bonding. (Top right) Probability distribution of the OH distance (bottom axis, unshaded), the NHO angle (dark shading), and the dipole-dipole angle (light shading) (top axis) in experimental backbone hydrogen bonds derived from a set of 138 proteins (Abagyan and Totrov, 1994). (Main graphic) Color-coded probability distribution for the dipole and NOH angles as defined in a. Dark areas indicate larger values.

This parameterization permits a continuous variation from a pure dipole-dipole model (X = 0) to the pure PMF model (X = 1) and represents short helix fragments best with the choice X = 0.25 and V₀ = 2.12 cal/mol Å. To determine optimal values for these parameters we optimized short helical fragments with several choices of the parameters and chose the values that stabilized structures closest to the experimental conformations. Solvation effects are described in a solvent-accessible surface area model that was fitted to the enthalpies of solvation of the Gly-X-Gly family of peptides (Eisenberg and McLachlan, 1986; Fauchere and Pliska, 1983) (see column in Table 2, all s_i = 1).

Optimization method

Monte Carlo with minimization has been used to locate the global minima of many complex potential energy surfaces (Li and Scheraga, 1987; Doyle and Wales, 1996; Wales and Doyle, 1997). The minimization step simplifies the potential energy surface (PES), by mapping each conformation to a nearby local minimum. The increase of efficiency of Monte Carlo with minimization in comparison to the Monte Carlo method (Metropolis et al., 1953) on the original potential energy surface strongly depends on the average energy gain in the minimization procedure. For models with very rugged potential energy surfaces, such as those encountered in protein folding with large-scale conformational changes per step, local minimization yields comparatively little improvement. We have therefore replaced each local minimization by a simulated-annealing (Kirkpatrick et al., 1983) run, starting at 660 K and then cooled with a geometric cooling cycle to 1 K. The number of steps in the cooling cycle is gradually increased, according to 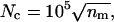with the number of the minimization cycle n_m. The resulting configuration replaces the starting configuration according to a threshold acceptance criterion with a threshold of 3 kcal/mol. During the simulated-annealing simulations, changes in the dihedral angles are generated randomly for both side-chain and main-chain dihedral angles. Global moves for the main-chain dihedral angles are additionally generated from a library (Avbelj and Moult, 1995a).

Free-energy surface topology

The topology of the low-energy part of the free-energy surface was analyzed in a decoy tree (Brooks et al., 2001; Becker and Karplus, 1997) that groups conformations in a given energy range into families. As a distance measure, we used backbone root mean-square deviation (BRMSD). The tree was constructed from all decoys (local minima that differ by at least 1 Å BRMSD from all other decoys) encountered in the simulations for a sequence of equidistant energies 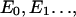starting with the energy of the best conformation. A decoy with energy below E_n that has <3 Å BRMSD to the decoy of just one family at the next lower energy level E_n–1 is included into that family. If a decoy is associated with more than one family, the corresponding families are united. If it belongs to no existing family a new family containing just this decoy is created. For each family we draw a vertical line in the energy window between E_n–1 and E_n and merge the lines for the energy E_n where the families are united. This analysis results in an inverted tree-like structure that illustrates the energetic order and degree of structural similarity of conformations via their family association. For a force field that stabilizes the native structure, the native family is represented by the branch of the tree that extends the furthest downward. In force fields that stabilize non-native structures, perturbations in the parameters can be used to rebalance the lower portion of the tree.

RESULTS

Force-field optimization

Using the modified basin hopping technique we generated ∼10,000 decoys for 1VII starting from both the NMR and stretched conformations, which resulted in many different conformations with energies below that of native decoys (Herges et al., 2004). We thus refitted the solvation parameters against improved data for the free energies of solvation (Sharp et al., 1991) using Sharke-Rupley (Sharke and Rupley, 1973) side-chain surfaces ( in Table 2). We reoptimized all low energy decoys of the previous simulations, which reduced the number (but did not eliminate the existence) of non-native decoys with energies below the NMR structure. We grouped these conformations into a decoy tree (Herges and Wenzel, 2004) and identified the set of most important unique competing structures to the native conformation.

The resulting free-energy landscape is illustrated in Fig. 2. All low energy decoys correspond to three-helix structures with nearly identical secondary content as the NMR structure. The decoy closest to the NMR structure (labeled N) has a backbone RMS deviation (BRMSD) of only 3.6 Å from the latter, but is not the global optimum of the PES. The global optimum is the three-helix structure labeled M in the figure, which has a BRMSD of 7.6 Å to the NMR decoy. The three helices in this structure have a different tertiary alignment than the NMR structure, with the direction of the last helix pointing in the opposite direction.

FIGURE 2.

Illustration of the low-energy part of the free-energy surface (top) of the villin headpiece with the unweighted solvation parameters ( in Table 2). The bottom of the figure shows the decoys corresponding to the five lowest terminal branches of the tree. Also shown is the NMR structure (labeled NMR) for comparison.

In a free-energy optimization approach, this failure to locate the correct global optimum points to a deficiency of the force field. A similar result was recently obtained for the same protein with the ECEPP/2 force field, where a competing two-helix structure emerged as the lowest energy decoy (Lin et al., 2003). The villin headpiece also failed to fold in an earlier landmark MD simulation (Duan and Kollman, 1998), but it is unclear whether limitations in the folding time or deficiencies in the force field were responsible.

Provided that the enumeration of metastable low energy structures of the free-energy surface in Fig. 2 is complete, small variations of force-field parameters will shift the energies of the decoys with respect to one another, but not introduce new branches in the tree. One may therefore attempt to rationally optimize the force field (Ulrich et al., 1997) to correctly fold the villin headpiece by computing the “gradient” of the energy differences between the terminal low-energy decoys with respect to the force-field parameters to stabilize the NMR structure against all other conformations. Once the force-field parameters have been modified, all low-energy decoys must be relaxed in the new force field and the same procedure is repeated until either the NMR structure emerges as the global minimum of the PES or several competing structures emerge with the same energy but gradients of opposite sign.

We thus optimized the force field to stabilize the NMR structure, concentrating on the parameters most difficult to obtain from first principles. The solvation model attempts to capture a whole host of complicated effects, including ion solvation, the hydrophobic effect, and side-chain entropy, in a very simple functional form. The translation of its experimental basis, the Gly-X-Gly transfer enthalpies from water to either vapor or octanol, into atomic solvation parameters depends strongly on the choice of the underlying peptide conformations. For these reasons, the free energies of solvation per unit area are the least-known parameters in the model. We therefore introduced amino-acid specific prefactors s_i into the solvation term to stabilize the NMR decoys against the competing low-energy structures following the strategy outlined above. In each iteration of this process all low-energy conformations of the decoy set, which ultimately included in excess of 76,000 structures grouped in to 14,000 decoy families, were relaxed. Using s_PHE = 1.2, s_MET = 0.9, s_LEU = 0.8, s_TRP = 0.6, and all other as s_i = 1, we ultimately arrived at a force field that stabilized an NMR decoy with 3.5 Å BRMSD against all competing structures (see Figs. 3 and 4).

FIGURE 3.

Decoy tree for the villin headpiece in the optimized force field. The structures corresponding to the terminal branches of the tree are shown in Fig. 4, their energies, BRMSD, and secondary structure content is shown in Table 3. The tree was constructed from a set of 76,000 structures grouped in 14,000 families as discussed in Methods.

FIGURE 4.

Native structure (labeled NMR) and the conformations of the terminal branches of the decoy tree of the villin headpiece. The labels refer to the branches in Fig. 3 and the numbers indicate the BRMSD to the native structure. The top right shows the C_β–C_β distance map (see Fig. 7) between the NMR conformation and decoy N.

The resulting free-energy surface is illustrated by the decoy tree shown in Fig. 3. The variation of the solvation parameters lead to a flattening of the free-energy surface, which now has seven almost-isoenergetic non-native terminal branches. The decoys associated with the terminal branches of the tree are shown in Fig. 4. There are now five 3-helix and two 2-helix structures at the bottom of their respective branches of the tree. The secondary structure, with the lowest energy conformations along with their BRMSDs and energies, are listed in Table 3. One notes a distinct propensity for the formation of helices in those regions where the NMR structure forms helices 1 and 3. The central helix occurs less often and leads to misfolded decoys reminiscent of the two-helix structures found in Lin et al. (2003). The energy spectrum shows a gap of 1 kcal/mol between the NMR decoy and the next competing structure, and becomes nearly continuous with increasing energy. An analysis of the BRMSD matrix of all low-energy decoys suggests that many distinct metastable conformations were probed in the search.

TABLE 3.

Lowest energy structures found in the analysis of the 1VII free-energy surfaces

F Kcal/mol	BRMSD [Å]		Secondary structure content
		NMR	cccHHHHHttssscHHHHttscHHHHHHHHHHttcc
−85.14	3.56	N	cccHHHHHHHHtscHHHHHHscHHHHHHHHHHHtcc
−84.11	6.36	B	cccHHHHHHtHHHHHHHHHHssscctttHHHHHHHc
−83.54	7.27	C	cHHHHHHHHHsssccsscscHHHHHHHHHHHHHtcc
−83.17	5.96	E	cHHHHHHHHHtssscsccssHHHHHHHHHHHHHtcc
−83.10	6.29		cccHHHHHHcHHHHHHHHHHsssccHHHHHHHHHHc
−82.59	6.40		cccHHHHHHcHHHHHHHHHHsssccHHHHHHHHtcc
−82.43	6.14	D	cHHHHHHHHtHHHHHHHHHHsssctttcHHHHHttc
−82.28	5.80	F	cHHHHHHcHHHHHHHHHHcHHHHHHHHHHHHHHHHc
−82.17	6.44		cccHHHHHHcHHHHHHHHHHsssccHHHHHHHHHHc
−82.03	7.85	A	cccHHHHHHHHtscHHHHHHsctttssssscctttc
−82.01	4.02		cccHHHHHttttccHHHHHHscHHHHHHHHHHcccc
−81.73	8.21		cccssccsctttHHHHtcccccsscHHHHHHHHtcc
−81.72	6.89		cccsHHHHHHHHHHHHHHHHsscttssccHHHHtcc
−81.49	4.85		cccHHHHHHHcHHHHHHHHsHHHHHHHHHHHHHtcc
−81.46	6.46		ccccHHHHHHHHHHHHHHcHHHHHHHHHHHHHHtcc
−81.35	7.62		cccHHHHHHHtssccsscscHHHHHHHHHHHHHtcc
−81.16	5.49		cccHHHHHHHHHHHHHHHHHscccscHHHHHHHHHc
−81.06	6.42		cccHHHHHHcHHHHHHHHHHsssccHHHHHHHHHHc
−80.98	7.74		cccHHHHHHHtssscsccssHHHHHHHHHHHHHtcc
−80.84	6.62		cccHHHHHHcHHHHHHHHHHsssccHHHHHHHHHHc
−80.79	4.46		cccHHHHHHHcHHHHHHHHsHHHHHHHHHHHHHtcc
−80.75	7.51		cHHHHHHHHHHtscHHHHsscsssctttccscsttc

Only structures which differ by at least 1 Å BRMSD from all other structures were included in the list. For each structure the free energy, its BRMSD from the native conformation and its secondary structure content, as computed by CSSP, is shown. The secondary structure content of the native conformation is shown on top for comparison. The labels refer to the decoys associated with the terminal branches of the decoy tree in Fig. 4.

Force-field validation

Using PFF01, we previously reproducibly and predictably folded two proteins, the 20-amino-acid Trp-cage protein (Neidigh et al., 2002; Simmerling et al., 2002; Schug et al., 2003) and the 40-amino-acid headpiece of the HIV accessory protein (PDB code 1F4I) (Herges and Wenzel, 2004). 1F4I is a three-helix protein with no homology to 1VII and folded reproducibly in 6 of 20 independent simulations. Competing low-energy conformers had similar secondary structure, but differed in the relative orientation of the helices. Trp-cage has a helix-turn-coil structure with significantly less helical content and exhibits two-stage folding on a 4-μs timescale. The tertiary structure of the protein was predicted correctly in 8 of 25 stochastic tunneling simulations (Wenzel and Hamacher, 1999; Schug et al., 2003); an analysis of the misfolded structures suggests that the formation of both helix segments is required to sterically permit the formation of the Trp-cage that stabilizes the tertiary structure of the native conformations. These data suggested that PFF01 may correctly predict the structure of a larger protein family.

We therefore investigated the transferability of the force field to three other helical proteins by extended decoy generation starting both from the NMR and from randomized structures. We first investigated Staphylococcus aureus protein A (PDB code 1BDD), where we selected the conserved helical section spanning 53 amino acids. Protein A was recently investigated with knowledge-based potentials (Zhou and Karplus, 1999), replica-exchange molecular dynamics (Garcia and Onuchic, 2003), and all-atom models (Vila et al., 2004). Fig. 5 illustrates the distribution of energy versus BRMSD for the random/NMR decoys in black/blue for the best of 48,000 generated decoys. The overlap in energy/BRMSD between the two datasets suggests that the random simulations covered a substantial fraction of the low-energy free-energy landscape of the protein. The conformations lowest in energy were NMR decoys that deviated ∼2 Å in BRMSD from the NMR structure, which defines the resolution of the force field. The best folded structure (diamond in Fig. 5) was <1 kcal/mol higher in energy than the best NMR decoy, which illustrates the required energy resolution of the optimization method for this protein. Stochastic optimization method cannot resolve the global optimum of the free-energy surface with absolute certainty; one must thus rely on repeated simulations to obtain reliable results for the relative energies of near-native and non-native decoys. Fig. 5 demonstrates the good overlap between the folded structure and the unrelaxed NMR conformation. The top section of Table 4 lists the energies of the best freely folded conformations and their deviation from the relaxed/unrelaxed NMR structures, respectively. Notably, all low-energy structures are very similar in their secondary structure content; almost all are three-helix structures. The lowest non-native decoys have a BRMSD of >8 Å but differ <2 kcal/mol in energy, which illustrates the demands on the resolution of the optimization method. As an alternate measure of structural similarity we have compared the C_β–C_β distances of the native and the decoy structure (Fig. 7). We find that 65% (80%) of the C_β–C_β distances of the decoy agree to within 1.5 (2.25) Å to the corresponding distances in the native structure. For the misfolded decoy, these values drop to 35% (44%) respectively, despite the fact that both conformations have nearly identical secondary structure.

FIGURE 5.

Correlation of energy and BRMSD of the low-energy section of the decoy set generated for protein A. Decoys obtained from randomized starting conditions are represented by solid symbols; decoys obtained starting from the NMR structure are represented by open symbols. The best estimates for the global optimum of the free-energy surface have only 2 Å BRMSD from the NMR structure. The diamond (see arrow) designates the best freely “folded” decoy for protein A, indicating that the efficiency of the optimization method, not the force field, is the limiting factor in folding larger proteins.

TABLE 4.

PFF01 energies and BRMSD (from the NMR structure and from the best NRM decoy) of the top-ranking decoys of the 1BDD, 1ENH, and 1GYZ proteins

Energy	BRMSD	BRMSD	Secondary structure classification
1BDD
−161.39	2.45	—	CCHHHHHHHHHHHHCSSCCHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHHC
−160.28	4.44	3.86	CCHHHHHHHHHHSSHHHHCHHHHHHHHHHHHHCTTCHHHHHHHHHHHHHHHC
−160.49	4.10	3.71	CCHHHHHHHHHHSHHHHHCHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHHC
−159.63	4.45	3.78	CCHHHHHHHHHHSSHHHHCHHHHHHHHHHHHHCTTCHHHHHHHHHHHHHHHC
−159.50	8.97	8.86	CCHHHHHHHHHHSSCHHHHHHHCHHHHHHHCHHHHHHHHHHHHHTCHHHHHC
−159.49	3.50	3.62	CCHHHHHHHHHHSHHHHHCHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHTC
−159.32	4.08	3.56	CCHHHHHHHHHHSSHHHHCHHHHHHHHHHHHHCTTCHHHHHHHHHHHHHHHC
−159.13	4.46	4.06	CCHHHHHHHHHHSSHHHHCHHHHHHHHHHHHHSSSCHHHHHHHHHHHHHHHC
−159.12	4.33	3.84	CCHHHHHHHHHHSSHHHHCHHHHHHHHHHHHHSTTCHHHHHHHHHHHHHHHC
−159.07	4.07	3.51	CCHHHHHHHHHHSSHHHHCHHHHHHHHHHHHHCTTCHHHHHHHHHHHHHHHC
−159.03	4.11	3.59	CCHHHHHHHHHHSSHHHHCHHHHHHHHHHHHHCTTCHHHHHHHHHHHHHHHC
−158.71	4.53	4.34	CCHHHHHHHHHHSHHHHHCHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHHC
−158.54	4.19	3.68	CCHHHHHHHHHHSSHHHHCHHHHHHHHHHHHHSTTCHHHHHHHHHHHHHHHC
−158.47	3.60	3.63	CCHHHHHHHHHHSHHHHHCHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHHC
−158.46	4.05	3.58	CCHHHHHHHHHHSCHHHHCHHHHHHHHHHHHHSSSCHHHHHHHHHHHHHHHC
−158.45	3.49	3.61	CCHHHHHHHHHHSHHHHHCHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHHC
−158.40	3.40	3.47	CCHHHHHHHHHHSHHHHHCHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHHC
−158.25	4.29	3.73	CCHHHHHHHHHHSSHHHHCHHHHHHHHHHHHHSSSCHHHHHHHHHHHHHHHC
−158.25	3.59	3.38	CCHHHHHHHHHHCHHHHHCHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHHC
−158.20	8.10	8.52	CCHHHHHHHHHHHHSHHHHHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHHC
−158.09	4.28	4.06	CCHHHHHHHHHHSHHHHHCHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHHC
−158.05	3.90	3.38	CCHHHHHHHHHHTTHHHHCHHHHHHHHHHHHHCTTCHHHHHHHHHHHHHHHC
−157.97	4.08	3.71	CCSSCHHHHHHHSHHHHHCHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHHC
−157.92	4.24	3.81	CCHHHHHHHHHHSCHHHHCHHHHHHHHHHHHHSTTCHHHHHHHHHHHHHHHC
−157.55	4.35	3.86	CCHHHHHHHHHHCSHHHHCHHHHHHHHHHHHHCTTCHHHHHHHHHHHHHHHC
−157.55	3.53	3.32	CCHHHHHHHHHHSHHHHHCHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHHC
−157.51	8.26	7.79	CCHHHHHHHHHHHHSCCCCHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHHC
−157.48	4.21	3.79	CCHHHHHHHHHHSCHHHHCHHHHHHHHHHHHHSTTCHHHHHHHHHHHHHHHC
1ENH
—	—	—	CCCCCCCHHHHHHHHHHHHHCSSCCHHHHHHHHHHHTCCHHHHHHHHHHHHHHC
−192.99	2.27	—	CHHHHSCHHHHHHHHHHHHHSSSCCHHHHHHHHHHHTCCHHHHHHHHHHHHHHC
−192.75	5.84	5.46	CHHHHHSHHHHHHHHHHHHHCHHHHHHHHHHHHHHHTSCHHHHHHHHHHHHHHC
−190.63	5.83	5.47	CHHHHHSHHHHHHHHHHHHHCHHHHHHHHHHHHHHHTCCHHHHHHHHHHHHHHC
−189.51	5.74	5.34	CHHHHHSHHHHHHHHHHHHHSHHHHHHHHHHHHHHHTSCHHHHHHHHHHHHHHC
−189.19	5.85	5.47	CHHHHHSHHHHHHHHHHHHHCHHHHHHHHHHHHHHHTSCHHHHHHHHHHHHHHC
−188.31	5.99	5.60	CHHHHTSHHHHHHHHHHHHHCHHHHHHHHHHHHHHHTSCHHHHHHHHHHHHHHC
−188.23	6.73	6.26	CHHHHHSHHHHHHHHHHHHHSHHHHHHHHHHHHHHHTSCHHHHHHHHHHHHHHC
−187.99	8.33	8.11	CCCHHHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHC
−187.30	5.82	5.54	CHHHHTSHHHHHHHHHHHHHCHHHHHHHHHHHHHHHTCCHHHHHHHHHHHHHHC
−187.16	5.72	5.26	CHHHHHSSHHHHHHHHHHHHSHHHHHHHHHHHHHHHTSCHHHHHHHHHHHHHHC
−187.11	6.50	5.99	CHHHHHSHHHHHHHHHHHHHCHHHHHHHHHHHHHHHTCCHHHHHHHHHHHHHHC
−186.75	6.09	5.70	CHHHHTSHHHHHHHHHHHHHSHHHHHHHHHHHHHHHTCCHHHHHHHHHHHHHHC
−186.29	8.44	8.24	CCCHHHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHCHHHHHHHHHHHHHHHHHC
−185.78	6.17	5.95	CHHHHTSHHHHHHHHHHHHHCHHHHHHHHHHHHHHHTCCHHHHHHHHHHHHHHC
−185.07	5.89	5.58	CCHHHHSHHHHHHHHHHHHHCHHHHHHHHHHHHHHHTCCHHHHHHHHHHHHHHC
−184.54	3.82	2.91	CCCCSSCHHHHHHHHHHHHHSCCCSHHHHHHHHHHHSCHHHHHHHHHHHHHHHC
1GYZ
—	—	—	CCHHHHHHHTTTTCCSHHHHHHHHHHTCCCCSSSSHHHHHHCHHHHHHHHHHHHHHTTCC
−154.23	1.61	—	CHHHHHHHHHHHTCCSHHHHHHHHHHTCCCSSSCSHHHHHHCHHHHHHHHHHHHHHHTTC
−152.48	5.78	5.58	CHHHHHHHHHHHTCSCSSSCHHHHHHTHHHHTCCCCHHHHHCHHHHHHHHHHHHHHHHTC
−150.18	5.95	5.84	CHHHHHHHHHHHTCCCSSSCHHHHHHTHHHHTCCCCHHHHHSHHHHHHHHHHHHHHHHTC
−147.65	5.13	5.04	CCCCCHHHHHHHTCCCHHHHHHHTCBTTTBSSCCCHHHHHHSHHHHHHHHHHHHHHHTTC
−147.65	5.54	5.43	CCCSSHHHHHHHTCCCHHHHHHHHTBTTTBSSCCCHHHHHHCHHHHHHHHHHHHHHSCCC
−147.24	5.33	5.29	CCSSCHHHHHHHTCCCHHHHHHHHTBTTTBSSCCCHHHHHHCHHHHHHHHHHHHHHSCCC
−147.19	5.32	5.23	CHHHHHHHHHHHTCCSSSSCHHHHHHTHHHHTCCCCHHHHHSHHHHHHHHHHHHHHTTCC
−146.69	5.64	5.56	CCCSSHHHHHHHTCCCHHHHHHHHTBTTTBSSCCCHHHHHHCHHHHHHHHHHHHHHSCCC
−146.30	5.27	5.11	CCCCCHHHHHHHTCCCHHHHHHHTTBTTTBSSCCCHHHHHHSHHHHHHHHHHHHHHTTTC

FIGURE 7.

Distance map comparing the C_β–C_β distances of the native structure with that of the best decoy (left) and the second-best decoy (right) of 1BDD. A pixel in row i and column j of the figure indicates the difference in the C_β–C_β distance of the native and the measured structure. Solid and shaded squares indicate that the C_β–C_β distances of the native and the other structure differ by <1.5 (2.25) Å, respectively. Open squares indicate larger deviations.

Motivated by a recent combined experimental and computational effort to elucidate its folding dynamics we investigated 1ENH, a 52-amino-acid, three-helix protein. As for 1BDD, NMR decoys were lowest in energy, which stabilizes the native structure to within 2.3 Å BRMSD. Freely folded decoys approached these conformations to 2.9 Å (third entry from the bottom of the second section of Table 4), but failed to reach sufficiently low energy to predictably fold the protein. Among the non-native decoys two important families at ∼6 and 8.5 Å BRMSD emerged, which had very similar secondary structure. In our validation study, we also investigated the bacterial ribosomal protein (PDB code 1GYZ) as an example of a four-helix protein. With 60 amino acids, this was the largest protein we have investigated so far. Its best NMR decoy deviates only 1.6 Å BRMSD from the NMR conformation, thus approaching experimental resolution. As for the other proteins, we found no structures lower in energy than the NMR structure; the best freely folded decoys approached the NMR structure to within 5 Å BRMSD and were 2 kcal/mol higher in energy.

DISCUSSION

Following the thermodynamic hypothesis (Anfinsen, 1973), which stipulates that a protein is in thermodynamic equilibrium with its environment, its native structure can be predicted as the global optimum of a suitable free-energy force field. Here we have described the rational parameterization of a free-energy force field, PFF01, for all-atom protein structure prediction.

Our all-atom representation of the protein permits the parameterization of the free-energy landscape on the basis of physical interactions that are well understood for smaller systems. Parameterizations based on physical interactions promise transferability, in particular to nonphysiological environments, and opportunities for rational development of the methodology in comparison to purely knowledge-based potentials. Our results suggest that a force field based on physical interactions in proteins benefits from the inclusion of heuristic corrections for complex interactions, e.g., screening effects of the implicit solvent and hydrogen bonding. The use of physical interactions in all-atom representations incurs a large computational cost when compared to more coarse-grained, or homology-based models. The elimination of explicit solvent degrees of freedom is a prerequisite for the applicability of the optimization approach. This work demonstrates that the entropic contributions arising from the contact with the solvent can be approximated by simple, computationally efficient models for realistic systems.

We find that PFF01 stabilizes the near-native conformation of several nonhomologous helical proteins against large independently generated decoy sets. One cannot overemphasize the importance of the interplay of optimization methods and force-field validation. Rational force-field development mandates the ability to generate decoys that fully explore competing low-energy conformations to the native state. The success of different optimization strategies depends strongly on the structure of the potential energy surface. As a result the development of efficient optimization techniques for all-atom protein structure prediction depends on the availability of a force field that stabilizes native conformations of proteins with appreciable hydrophobic cores. For helical proteins the bottleneck in ab initio all-atom structure prediction now lies in the development of optimization strategies that significantly increase the system size that can be treated with present day computational resources. Force-field validation for larger proteins, for which low-energy decoys are difficult to generate at the all-atom level, may thus employ existing sets of independently generated decoys (Nanias et al., 2003).

Our results indicate that for helical proteins the bottleneck toward the treatment of larger systems is the efficiency of the optimization method, rather than the quality of the force field. The availability of PFF01 provides a framework for the development of new optimization strategies for larger molecules.

We hope that the rational strategy of all-atom force-field optimization pursued in this project offers a valuable contribution to protein structure prediction in general. Even if the available computational resources remain insufficient in the foreseeable future to fold large proteins, all-atom force fields may be used to discriminate and refine among conformations generated on the basis of other techniques, in particular with coarse-grained, or knowledge-based potentials (Nanias et al., 2003).

FIGURE 6.

Stereo view of the overlay of the secondary structure representation of the unrelaxed NMR (green) and freely folded (red) conformations of protein A. Inspection of the conformations indicates that two helices were perfectly folded, whereas the last helix lacks a turn which hinders its relative orientation with respect to the other two helices.