Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Nov 12;88(2):1081–1090. doi: 10.1529/biophysj.104.042788

Dynamic Properties of an Oriented Lipid/DNA Complex Studied by Neutron Scattering

F Natali *, C Castellano †, D Pozzi †, A Congiu Castellano †
PMCID: PMC1305114  PMID: 15542564

Abstract

The formation of lipid-DNA (CL-DNA) complexes called lipoplexes, proposed as DNA vectors in gene therapy, is obtained by adding DNA to a solution containing liposomes composed of cationic and neutral lipids. The structural and dynamic properties of such lipoplexes are determined by a coupling between the electrostatic interactions and the elastic parameters of the lipid mixture. An attempt to achieve a better understanding of the structure-dynamics relationship is reported herein. In particular, an elastic neutron scattering investigation of DOTAP-DOPC (dioleoyl trimethylammonium propane-dioleoyl phosphatidylcoline) complexed with DNA is described. Proton dynamics in this oriented CL-DNA lipoplex is found to be strongly dependent upon DNA concentration. Our results show that a substantial modification of the membrane dynamics is accompanied by the balancing of the total net charge inside the complex, together with the consequent displacement of interlayer water molecules.

INTRODUCTION

The success of gene therapy, defined as the transfer of nucleic acids to the somatic cells of an individual, is largely dependent on the development of a vector which can selectively and efficiently deliver a gene to target cells (Friedmann, 1997; Rubanyi, 2001).

Cationic liposomes, closed membrane shells of lipid molecules, commonly known as lipoplexes when complexed with DNA (CLs-DNA) (Felgner et al., 1987; Rubanyi, 2001) have attracted an increasing level of attention as nonviral vehicles for delivering genes into mammalian cells.

Many theoretical and experimental studies have been performed (Cullis and de Kruijff, 1979; Farhood et al., 1995; Liu et al., 1997; Radler et al., 1997; Crook et al., 1998; Hirsch-Lerner and Barenholz, 1999; Kennedy et al., 2000; Regelin et al., 2000; Choosakoonkriang et al., 2001; Braun et al., 2003) to understand the factors governing the energetic, structural, and thermodynamic characteristics of CL-DNA complexes; these properties, strongly influenced by the specific composition of lipoplexes, are essential for optimizing their transfection efficiency. The cationic lipoplexes are normally constituted by the mixture of a neutral (helper) lipid and a charged lipid; the former determines a given structure (in particular lamellar or hexagonal geometry), whereas the latter is fundamental for delivering the genes into the cell (Radler et al., 1997; Rubanyi, 2001; Zuhorn et al., 2002).

It has been assumed for some time now that the transfection efficiency of inverted hexagonal complexes (Inline graphic) is higher than that of lamellar complexes 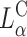Inline graphic in all the cell lines studied (Cullis and de Kruijff, 1979; Farhood et al., 1995; Safinya, 2001).

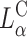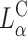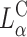In a recent study Lin et al. (2003) identified the membrane charge density σM of the CL-vector (i.e., the average charge per unit area of the membrane) as a key universal parameter that determines the transfection efficiency behavior of Inline graphic complexes in the cell. By modulating this parameter it is possible to obtain Inline graphic complex efficiencies as high as that of Inline graphic complexes. In contrast to Inline graphic complexes, Inline graphic 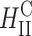complexes exhibit no dependence on σM. This indicates that transfection efficiency depends on a structural parameter (lamellar or columnar inverted hexagonal structure) combined with physical-chemical parameters.

The direct interaction of the positively charged lipid headgroup with the negatively charged phosphate of the DNA backbone is suggested by many authors to be the main mechanism for the complexation of DNA with cationic lipids (Kennedy et al., 2000; Choosakoonkriang et al., 2001). This is also supported by both fluorescence techniques and differential scanning calorimetry (Hirsch-Lerner and Barenholz, 1999) suggesting that the release of bound water and counterions is the driving force behind complex formation (Kennedy et al., 2000). Besides, Choosakoonkriang and co-workers suggest that complexation with DNA induces a small increase in the disordered conformation of the lipid alkyl chain, altering the packing of the lipid (due to the alignment of the lipid headgroup with the DNA phosphate) and determining a greater fluidity of the apolar region of the membrane (Regelin et al., 2000; Choosakoonkriang et al., 2001).

Unfortunately, very few studies have been performed on the dynamics of CLs-DNA systems to date. In this context computer simulation studies of model biological membranes were recently carried out (Bandyopadhyay et al., 1999; Saiz and Klein, 2002a,b) in the fluid lamellar phase of the lipid-DNA complex containing DMPC and DMTAP lipids at the isoelectric point. The configuration after 5.5 ns suggests that the presence of the DNA sandwiched between two lipid-water interfaces, induces significant undulations of the membrane surface, indicating a strong interaction between the lipid interface and the DNA.

This work is aimed at studying the structure-dynamics relationship, and the dependence of dynamics on the composition of the lipids mixture and on the lipid-DNA ratio.

This investigation takes advantage of the great utility shown by neutrons in the study of biological macromolecules. Indeed, unlike x rays, which interact with matter via electrons, neutrons are not invasive in biology since, as they interact only with the nuclei, they do not lead to radiation damage of the sample. Thus, experiments are not limited to the low T range, but can be extended to higher temperatures over the range of physiological conditions. Moreover it is known that incoherent elastic neutron scattering provides unique information on the protons present in a sample due to the high hydrogen incoherent cross section (σinc) with respect to the total (coherent and incoherent) scattering cross section of the other atoms (Bée, 1998). Indeed the probability per nucleus that a neutron in the beam will interact with the nucleus itself is expressed in terms of an equivalent area (the cross section) that the neutron “sees”. The scattering is called coherent when it depends on the correlation between the position of the same nucleus at different times, and on the correlation between the positions of different nuclei at different times; otherwise the scattering is called incoherent when it depends only on the correlation between the positions of the same nucleus at different times (Squires, 1997).

The combination of the extremely large hydrogen incoherent cross section with the great abundance of this atom in biological macromolecules (easily as much as 50%) makes the neutron scattering technique a powerful tool for studying the dynamics of biological systems. In particular, in this work, neutron elastic incoherent scattering was utilized to study the dynamics of the lipoplexes as a function of DNA concentration.

We focus on CLs-DNA complexes consisting of 1:1 ratio binary mixtures of cationic monovalent lipid DOTAP (dioleoyl trimethylammonium propane) and the neutral helper lipid DOPC (dioleoyl phosphatidylcholine), both lipids having two 18-carbon (C18) aliphatic chains per molecule. Appropriate amounts of calf thymus DNA are then added.

The choice of lipoplex has been suggested by results obtained by J. O. Radler and co-workers (Radler et al., 1997) using high-resolution synchrotron x-ray diffraction and by us (Caracciolo et al., 2002a,b) using energy dispersive x-ray diffraction; both experiments show that the DOTAP-DOPC/DNA packing has an ordered multilamellar structure, Lα, with the DNA sandwiched between cationic bilayers. Indeed, the helper-lipid DOPC and the cationic lipid DOTAP have cylindrical shapes, with the headgroup areas approximately equal to the hydrophobic tail areas, thus tending to self-assemble into lamellar structures. Indeed in this case, as reported elsewhere (Safinya, 2001), the natural radius (R0) of the monolayer tends toward infinity and the natural curvature C0 = 1/R0 tends to zero.

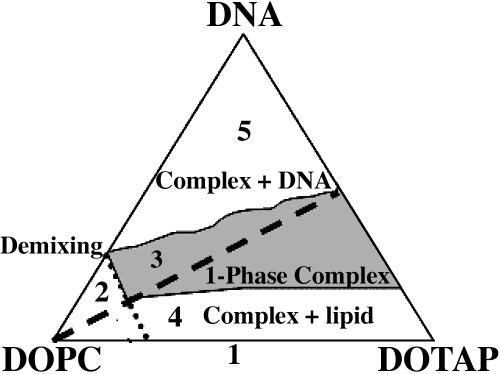
In Fig. 1 we show the phase diagram of the lamellar Lα CL-DNA complexes as built up by Koltover et al. (1999). The broken line represents the isoelectric point.

FIGURE 1.

FIGURE 1

Open in a new tab

Phase diagram of the lamellar CL-DNA complexes. Corners of the triangle correspond to 100% weight fraction of DOPC, DOTAP, and DNA. Dashed line indicates the isoelectric DOTAP/DNA ratio (adapted from Koltover et al., 1999).

Thus, five different regions seem to characterize the phase diagram: 1), the DNA-free DOPC/DOTAP CL regime; 2), the DOPC/DOTAP demixing regime, appearing at very low cationic concentrations; 3), the single phase CL-DNA complex; 4), the coexistence of CL-DNA complex with an excess of lipid molecules; and 5), the coexistence of CL-DNA complex with an excess of DNA molecules.

The main goal of this work is to add to the already available electrostatic and structural information a first dynamical characterization of this lipoplex in the most physiologically interesting system condition, i.e., in the one-phase complex (region 3 in the phase diagram),

For this purpose let us recall some of the main results available in literature on the above-cited systems, which may help us in our investigation. In particular, Roux and Safinya (Roux and Safinya, 1988; Safinya, 1989) suggest that, in the absence of DNA, the lamellar Lα phase of DOPC/DOTAP CL membranes exhibits strong long-range interlayer electrostatic repulsions that overwhelm the van der Waals attraction. Moreover, the interlayer spacing d, as determined by Safinya (2001), is found to depend on the amount of water present in the complex according to the relation d = δm/(1−Φw) (where Φw is the volume fraction of water and δm is the membrane thickness). For CL complexes at DOPC/DOTAP 1:1 ratio, the value obtained is δm = 39.0 ± 0.5 Å. The average thickness of the water gap (δw = d − δm = 64 Å − 39 Å = 26 Å) allows one monolayer of DNA (diameter ∼20 Å in the B form) to be contained, together with its first hydration shell (Safinya, 2001).

Through DNA-lipid complexation, the cationic lipid tends to fully neutralize the phosphate groups on the DNA, replacing and releasing counterions in solution. Conversely, whereas on the one hand the counterion release mechanism plays a key role in the CL-DNA complex formation, this represents a strong limitation, favoring the formation of only charge-neutral complexes (shown by the dashed line in the phase diagram, Fig. 1). Indeed, Bruinsma and co-workers have shown that the lipoplex at the isoelectric point, when the complete charge balance is reached between the positively charged cationic lipids and the negatively charged DNA chains, is unstable against adsorption of extra DNA or lipid molecules (regions 4 and 5 of Fig. 1). This instability is determined by the entropy gain occurring when small ions are released inside the complex and is clearly observable in the behavior of the dDNA spacing near the isoelectric point (Bruinsma, 1998).

However, since the CL-DNA complexes must be cationic to bind to cell surface, it is extremely important to extend our study to charged CL-DNA lipoplexes.

MATERIALS AND METHODS

Cationic liposome preparation

Lamellar CL-DNA complexes were prepared as described in detail elsewhere (Caracciolo et al., 2002a,b, 2003). Lipids and DNA were purchased from Sigma (St. Louis, MO). The mixtures of cationic lipid dioleoyl trimethylammonium propane (DOTAP) (molecular weight = 698.6) and helper lipid dioleoyl phosphatidylcoline (DOPC) (molecular weight = 705) were prepared by choosing the fraction of weight of DOPC/total lipid weight (Φ) = 0.5. An appropriate amount of double-stranded calf thymus DNA (molecular weight (basepair) = 649) was diluted in deionized water and then sonicated for 1 min; the molecular weight distribution in the solution, determined by gel electrophoresis, was within 0.5–1 kb.

Oriented multilayers were obtained by depositing the final solution on (110) Si wafers (30 × 40 × 0.15 mm3); the samples were dried in a closed chamber under a gentle nitrogen flux and stored at T = 40°C for several hours. The mosaic spread of the lipid mixture was determined by x-ray diffraction: the angular width of the first order Bragg reflection, estimated as <1°, confirms the good quality of the oriented multilayers (Natali et al., 2002, 2003).

A total number of five wafers (four wafers covered with the CLs-DNA film and one bare wafer) were layered in a slab-shaped aluminum sample holder vacuum-tight using an indium seal. To prevent sample contamination the sample holders were gold coated.

Three different samples were investigated: a), CLs binary mixture without DNA (here called lipids); b), CLs-DNA with excess of lipids (ρ = 4); and c), CLs-DNA at the isoelectric point.

Since DNA carries two negative charges/basepair, whereas each DOTAP molecule has one positive charged head group, the complex at the isoelectric point is stoichiometrically neutral only when the numbers of DNA bases and DOTAP molecules are equal or when ρ = ρISO ≅ 2.2, where

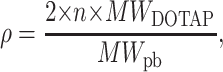graphic file with name M8.gif (1)

with n the number of DOTAP molecules per DNA basepair (pb), and MW the molecular weight.

We have not investigated the CL-DNA mixture with ρ < ρISO (excess of DNA) due to DNA precipitation at the high solution concentration required by neutron experiment.

Backscattering spectrometer

Incoherent elastic neutron scattering scans have been performed at the thermal (λ = 2.23 Å) backscattering spectrometer IN13 at ILL, taking advantage of the good energy resolution ∼8 μeV, thus allowing the investigation of a time window centered at ∼0.1 ns.

The elastic scattering intensities I (Q,ω = 0) were corrected for the contribution of the “empty” cell (containing five silicon wafers without CL-DNA complex) and normalized with respect to the lowest temperature run to compensate for spurious background contributions and detector efficiency.

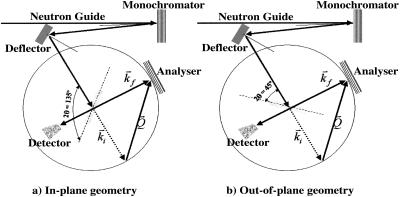
The selective investigation of lipid motions was achieved through the availability of oriented membranes, using Si (110) wafers as substrates. Thus, by rotating the sample with respect to the incoming beam, as shown in Fig. 2, the momentum transfer was oriented predominantly parallel and perpendicular to the membrane surface to detect in-plane (panel a) and out-of-plane (panel b) membrane dynamics, respectively.

FIGURE 2.

FIGURE 2

Open in a new tab

By rotating the sample with respect to the incoming beam, the momentum transfer is predominantly oriented parallel (panel a) and perpendicular to the membrane surface (panel b).

The in-plane motions are those lipid motions that have their main component on the membrane plane whereas the out-of-plane motions are those motions that have their main component along the normal to the membrane plane.

RESULTS

To understand complex dynamics, it is necessary to clarify: i), the origin of the measured incoherent neutron scattering signal (i.e., if the changes observed in the dynamics can be attributed only to lipid motion neglecting DNA dynamics), and ii), the kind of motion detected by our experimental setup.

In Table 1 we report the contributions, expressed in relative percentages, to the total proton scattering (coherent and incoherent) arising from DOTAP + DOPC (where the two lipids contribute equally to the scattering signal) and from DNA in the lipids mixture at two DNA concentrations (ρ = 4 and ρ = ρISO = 2.2).

TABLE 1.

Contributions, expressed in relative percentages, to the total proton scattering (coherent and incoherent) arising from DOTAP + DOPC (where the two lipids equally contributes to the scattering signal) and DNA in the lipids mixture and at two DNA concentrations (ρ = 4 and ρ = ρiso = 2.2)

Lipids (%) ρ = 4 (%) ρ = 2.2 (%)
DOTAP + DOPC 100 95.3 91.6
DNA 0 4.7 8.4
Open in a new tab

It is clear that the measured signal is assigned principally to the protons of the lipid hydrocarbon chains. Therefore, a second reason for excluding the ρ < ρISO CL-DNA samples (excess of DNA) from this investigation, is that the scattering signal from the DNA could mask the scattering signal of the lipid chains.

It is thus certain that an elastic experiment carried out on those systems might be useful in clarifying a), the dynamics of H atoms, here mainly located in the lipid chains, present in the DNA-free sample (lipids); and b), the changes induced on the lipid motion under DNA complexation.

The second question to answer refers to the specific motions observable in the experiment described herein.

As already mentioned, the experiment was performed at the IN13 high-energy resolution backscattering spectrometer at ILL (Grenoble). The high-energy resolution, provided by the backscattering geometries of the monochromator and analyzers of the spectrometer, was experimentally determined and found equal to ∼8 μeV. The corresponding time domain was then obtained by the Heisenberg uncertainty principle, ΔE × Δt = ℏ, leading to ∼0.1 ns.

Thus motions characterized by timescales within the time window centered at 0.1 ns fall within the elastic energy range accessible on IN13 and only these motions will be observable in our experiment. As reported elsewhere (Essmann and Berkowitz, 1999), this time domain covers typical dynamics of lipid molecules of oriented membranes: the chain defect motion, the rotational diffusion of the lipid molecule about its molecular axis and spatially restricted vertical translational diffusion. The first two motions are both in the membrane plane whereas the last is the typical out-of-plane motion that may be detected in the time window mentioned. We stress, on the other hand, that the estimated time domains of the motions mentioned are highly dependent on membrane composition, so that no specific assignment can be made without appropriate and detailed investigations. Therefore this work is a preliminary study based on the above-mentioned estimations, but further experiments, in particular quasi-elastic neutron scattering (QENS) scans have been planned for the same and complementary time domains. For this purpose, larger timescales have already been explored using the NEAT spectrometer at the HMI (Germany, data analysis in progress). We mention here how QENS measurements will make it possible to better characterize motion nature, thus obtaining also other quantitative information from the dynamic models chosen to interpret the data.

As already described in the Material and Methods section, as the experiment described herein is direction sensitive, the neutron scattering intensities were acquired at two different geometrical configurations, with the momentum transfer predominantly parallel and perpendicular to the membrane surface. Thus, information can be obtained on the in-plane and out-of-plane lipid motions in oriented systems (Fig. 2).

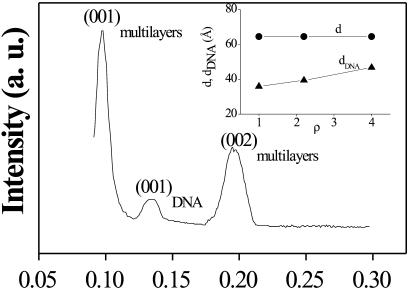
The typical mismatch of the bilayers and the quality of the samples were checked in our previous energy dispersive x-ray diffraction (EDXD) experiment (Fig. 3), where first- and second-order Bragg reflections reveal the existence of a bilayer periodicity of d ≅ 65.1 Å (Caracciolo et al., 2002a). This periodicity is in agreement with that obtained by Safinya (2001). An additional middle peak is observed in the EDXD scans corresponding to the average interhelical spacing between the DNA chains (dDNA), which has been observed to move from 35.1 to 47.7 Å, decreasing DNA concentration (inset, Fig. 3). Therefore the existence of two different packing regimes assigned to the positively charged and negatively charged CL-DNA complexes is revealed: the former are strongly influenced by the interbilayer repulsions that set the finite amount of lipid that the complex can accommodate, whereas the latter are influenced by inter-DNA repulsions (Caracciolo et al., 2003).

FIGURE 3.

FIGURE 3

Open in a new tab

EDXD scan of CLs-DNA measured at ρ = 4. The peaks are assigned to first (001) and second (002) orders of multilamellar Bragg reflections and to first (001) order interhelical DNA Bragg reflection. (Inset) dependence of the lamellar and of the DNA chains d-spacings upon the DNA concentration (Caracciolo et al., 2002a).

The agreement between the packing regimes and the EDXD data, as expected, confirms the model in which the CLs and DNA condense into a multilayer structure with DNA sandwiched between the bilayers (Radler et al., 1997). Moreover, the first dDNA Bragg peak is broader than the lamellar ones ((HWHM)Q(001)DNA = 0.0058 Å−1, (HWHM)Q(001)multilayers = 0.00668 Å−1), as expected, because the two-dimensional smectic liquid crystal is more strongly affected by thermal disorder than the three-dimensional smectic one of the bilayer-DNA (Salditt et al., 1997).

These diffraction results showing a structural change due to the presence of DNA in the lipid bilayer afford us a better understanding of the influence of the DNA on lipid dynamics.

Dynamic models

Although elastic scattering does not allow any distinction to be made between different motions falling within the instrumental resolution window, we can try to find a proper model to describe the global dynamics. Thus, to apply a model to our investigation, the experimental mean-square displacements have to be extracted. This was done within the framework of the Gaussian model. In this context the normalized Q2-dependent elastic intensities were fitted in the low Q range to verify the condition of the Gaussian approximation, as described elsewhere (Doster et al., 1989; Reat et al., 1997; Natali et al., 2000, 2002, 2003), using the following equation:

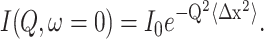graphic file with name M9.gif (2)

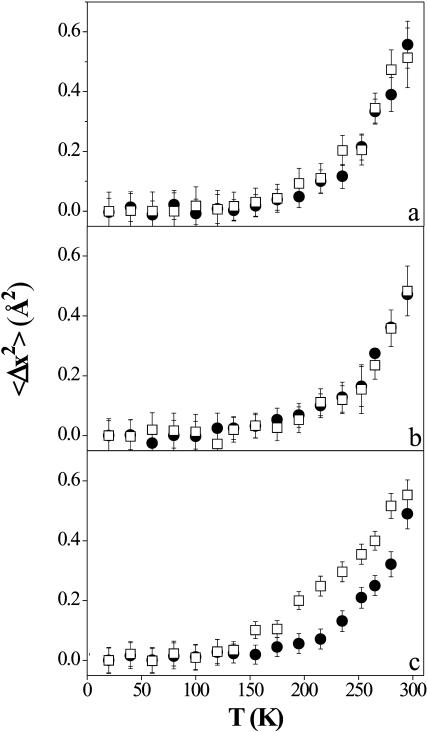
In Fig. 4 we report the normalized mean-square displacements thus obtained (〈Δx2〉 = 〈x2〉T − 〈x2〉20K) versus T of the lipids (DNA-free CLs), in panel a, and of CLs-DNA for ρ = 4, in panel b. No anisotropy is observed in these samples, suggesting that lipid dynamics have no preferential directions.

FIGURE 4.

FIGURE 4

Open in a new tab

Normalized mean-square displacements of the CLs-DNA mixed multilayers versus T, obtained in the framework of the Gaussian model. (Panel a) lipids; (panel b) ρ = 4; and (panel c) ρISO = 2.2. (Open squares) Out-of-plane direction; (solid circles) in-plane direction. The error bars are calculated as the standard deviation of different measures at the same temperature.

On the other hand, panel c, which refers to CLs-DNA at the isoelectric point, displays a marked anisotropy in the mean-square displacements. Therefore a higher dynamics associated with the vertical translation of lipids within the bilayer is observed in the out-of-plane configuration only when the complex is at the isoelectric point (Deriu, 1993).

Hitherto the elastic data concerning the atomic motions in proteins and membranes have been analyzed by preferentially considering two models essentially based on fluctuations between potential wells within the particle energy.

In particular, a two-state model was proposed by Doster and co-workers (Doster et al., 1989), in which the protons can fluctuate between two sites of different energy separated by a temperature-independent distance d.

A second and more complex model was recently introduced by Bicout and Zaccai (2001). It assumes the atomic motion in macromolecules to be fluctuating, within the energy conformational landscape, mainly between two classes of cages, in which the atoms accomplish small and large amplitude motions with respect to their equilibrium positions.

Because the aim of this work is to find the best model to describe the effect induced by the DNA on the CLs-DNA dynamics, both models have been considered.

In a first attempt, the data were analyzed using the two-state model (Doster et al., 1989). Unfortunately, the model properly describes only the low temperature range of our data, where the harmonic regime contributes exclusively to the mean-square displacements. The settling of additional degrees of freedom at higher temperatures suggests that a change in atom dynamics, usually called in neutron studies dynamical transition (Bicout and Zaccai, 2001), may eventually occur.

An extension of the model proposed by Doster (Doster et al., 1989), in which the vibrational motions in the two wells were assumed to be identical, is provided by the more sophisticated Bicout and Zaccai model which takes into account additional degrees of freedom accessible to the macromolecules. Indeed, the Bicout and Zaccai model considers different vibrational motions in each well, and regards the translational interconversion between wells as a continuous process. Therefore the nonharmonic regime observed in the mean-square displacements behavior may be assigned here to the crossing of the barrier separating the conformational cages in translational motions.

These cages represent the large or small environments within which the atomic motion occurs; it is common in quasielastic neutron scattering to speak of motions restricted within a cylinder or a sphere, etc., indicating the geometrical characteristics of such cages.

In this elastic experiment we have no quantitative information about the geometry of the cages as obtained by quasielastic scattering but we have some information on the variation of the atomic dynamics (i.e., mean-square displacements) inside them.

In this context, the mean-square displacement 〈R2(T)〉 (with 〈R2(T)〉 = 3 〈x2(T)〉), counting both the vibrational and translational motions of the particles, is given by

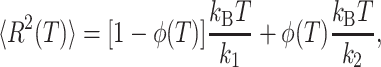graphic file with name M10.gif (3)

with Φ

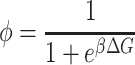graphic file with name M11.gif (4)

the probability of spanning a given potential well (Φ = 1 and Φ = 0 represents the limit when only small or large amplitude motions are observed, respectively). On the other hand, k1 and k2 are the force constants governing the particle motions in the small and large conformational cage, respectively. The model adopted here in the approximation of dynamically equivalent particles, turns out to be particularly suitable for describing atomic motion across a dynamical transition. The temperature at which the dynamical transition takes place (T0) is operatively defined by Bicout and Zaccai as the temperature at which ∼10% of the molecule fluctuations are of large amplitude. It is therefore clear that T0, which is strongly dependent on the energy difference between the conformational cages, is an optimal parameter for comparing molecular dynamics in different systems or/and in different environmental conditions. T0 is a reference temperature around which the length scale of dynamics changes and so we can speak of a transition between different kinds of cages or environments. Taking into account the settling of a dynamical transition, the expression of the mean-square displacements becomes

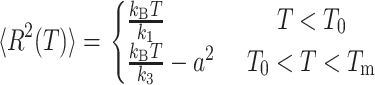graphic file with name M12.gif (5)

with

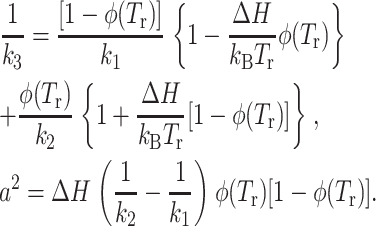graphic file with name M13.gif (6)

Tm is the temperature at which the energy-entropy compensation is reached (φ (Tm) = 0.5) and is generally higher than the maximum temperature explored in a standard experiment.

Thus, the pseudo-force constant k3 together with the forces constants k1 and k2, providing information on the resilience of the molecules are very useful for comparing different systems showing comparable transition temperatures (Zaccai, 2000).

An exhaustive description of different applications of the model to proteins and membranes is provided by Bicout and Zaccai (2001).

To enhance insight into this peculiar behavior, the Bicout and Zaccai model may now be applied to fit the data shown in Fig. 4 using Eqs. 3 and 5.

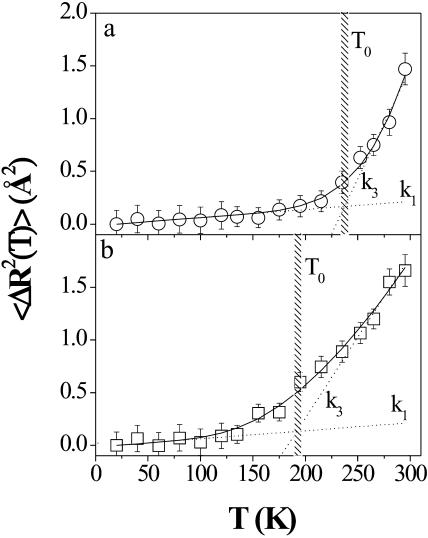
Fig. 5, by way of example, shows the results obtained for the mean-square displacements of the CLs-DNA at the isoelectric point (with 〈ΔR2(T)〉 =3 〈Δx2 (T)〉).

FIGURE 5.

FIGURE 5

Open in a new tab

Proton mean-square displacements (with 〈ΔR2(T)〉 = 3 〈Δx2 (T)〉) versus T for in-plane (panel a) and out-of-plane (panel b) configurations of CLs-DNA at the isoelectric point. The solid line is the best fit to the data using Eq. 3, whereas the dashed curves represent Eq. 5 with the force constants k1and k3. The error bars are calculated as the standard deviation of different measures at the same temperature.

Panels a and b refer to the in-plane and out-of-plane configurations, respectively. The continuous lines represent the best fit using Eq. 3 with ΔG, k1, and k2 as free parameters, whereas the dashed curves correspond to Eq. 5 with k1 and k3 the force and pseudo-force constants. The agreement between the experiment and the model is excellent.

The crossover between the two dashed curves indicates the settling of a dynamical transition between small and large conformational cages, with consequent univocal determination of the dynamical transition temperature T0. Fig. 5 clearly displays a significant difference in the observed T0.

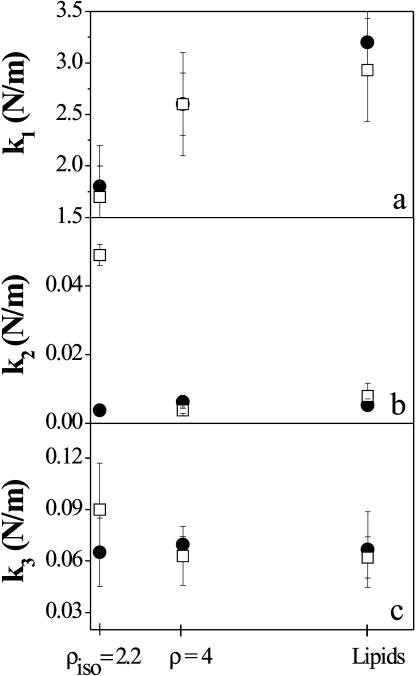
The fitting parameters thus obtained, k1 (panel a), k2 (panel b), and k3 (panel c) are reported as a function of the DNA concentration in Fig. 6.

FIGURE 6.

FIGURE 6

Open in a new tab

Dependence of k1 (panel a), k2 (panel b), and k3 (panel c) upon the DNA concentration. (Solid circles) In-plane direction; (open squares) out-of-plane direction. The data errors are calculated as statistical errors from the fit.

The two curves shown in each panel (Fig. 6) refer to the in-plane (solid circles) and out-of-plane (open squares) directions of the CLs-DNA with respect to the incoming neutron beam.

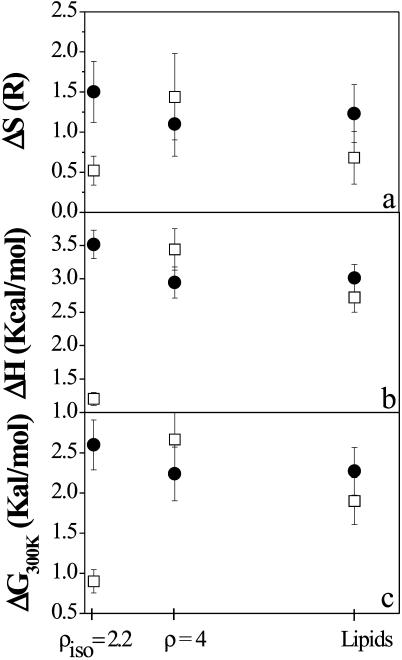
Fig. 6 suggests that the anisotropic behavior of the lipid motion at the isoelectric point lies in the temperature region where the dynamical transition may take place. Indeed, whereas the low temperature ranges of the two configurations of the CLs-DNA at ρ = 2.2 are characterized by similar force constants k1 (Fig. 6, panel a), as is suggested also by the absence of deviation in panel c of Fig. 3 at T < 150 K, the force constant k2 exhibits a strong increase in the out-of-plane geometry. On the other hand, a smaller free energy difference ΔG is observed as shown in Fig. 7, where ΔH and ΔS are also reported. This would suggest that the probability of interconversion between small and large amplitudes cages is strongly increased (Eq. 4), whereas the high amplitude motions cage of the DNA-lipoplex at the isoelectric point at 45° is characterized by smaller mean-square displacements (varying 〈ΔR2〉 with 1/k2, Eq. 3) with respect to the other compounds, indicating a conformation with reduced mobility and thus a dynamics inside a smaller conformational cage.

FIGURE 7.

FIGURE 7

Open in a new tab

Dependence of ΔS (panel a), ΔH (panel b), and ΔG300K (panel c) upon the DNA concentration. (Solid circles) In-plane direction; (open squares) out-of-plane direction. The data errors are calculated as statistical errors from the fit.

Once the dynamical transition has taken place, the equilibrium between the free energies and the force constants k2 contributions (Eq. 6) leads to comparable pseudo-force constants k3 (Fig. 6, panel c).

Thus, it turns out that an extremely useful parameter for characterizing the influence of the DNA concentration upon lipid dynamics is the dynamical transition temperature T0, shown in Fig. 8 as a function of the DNA concentration and for both geometrical configurations. The free energy difference, calculated at T = T0, is also shown in panel b.

FIGURE 8.

FIGURE 8

Open in a new tab

Dependence of the dynamical transition temperature T0 (panel a) and of the free energy calculated at T = T0 (panel b), upon the DNA concentration. (Solid circles) In-plane direction; (open squares) out-of-plane direction. The data errors are calculated as statistical errors from the fit.

The balancing of the net charge of the membrane by DNA molecules seems therefore to play a key role in enhancing the out-of-plane motion of the lipid chains, shifting the dynamical transition toward appreciably lower temperatures. This is accompanied by a strong deviation of ΔGT0, which indicates that interconversion between small and large atomic amplitude motion cages across the transition temperature is energetically favored in the out-of-plane membrane direction. Indeed ΔG is the free energy barrier that the particles have to cross to enter the large amplitude range or dynamical cage and the transition temperature depends upon this energy gap between conformational cages. On the other hand, the much higher force constant k2 indicates that the amplitudes in the high energy cages are not comparable in the three samples, since the mean-square displacements vary as 1/k2.

DISCUSSION

The results obtained here show that the DNA-free CLs complex displays an isotropic behavior in lipid dynamics. On the other hand, the frequently observed higher mobility in the out-of-plane direction of model membranes (König et al., 1992; Natali et al., 2003) may be screened and obstructed here by the interlayer repulsion. Indeed, as already mentioned in the introduction section, in the absence of DNA, the lamellar Lα phase of CL membranes exhibits strong long-range interlayer electrostatic repulsions that overwhelm the van der Waals attraction (Roux and Safinya, 1988; Safinya, 1989). The description, using several models, of the possible motions implied in the anisotropic behavior, is provided elsewhere on model membranes in the presence of stabilizing protein and has applications in neurophysiology (Natali et al., 2003).

We are confident in the model applied as the thermodynamic parameters obtained here are of the same order of magnitude as those obtained for other membranes (Bicout and Zaccai, 2001).

Through CLs-DNA complexation, the electrostatic repulsion is almost neutralized. The formation of higher-order self-assembly is thus favored by the replacement and release of the counterions in solution (>95% of the Na+ and Cl− from DNA and lipids, respectively) originally confined close to the DNA chains and lipid membrane surface (Manning, 1969). Indeed, this release mechanism, which accompanies CLs-DNA complex formation, leads to a high entropy gain (kBT/released counterion, comparable to the direct electrostatic repulsion) (Radler et al., 1997; Bruinsma, 1998; Harries et al., 1998; Wong et al., 2000), thus promoting a close association between DNA and lipids in a compact complex (Koltover et al., 2000). The CLs-DNA ordered structure thus formed shows an increased fluidity of the apolar region of the membrane, with respect to the DNA-free CLs systems (Regelin et al., 2000; Choosakoonkriang et al., 2001).

Together with counterions release, also the spatial dimension available to DNA plays a key role in the organization of the lipoplex, through the interactions between chains. Indeed, to minimize the long-range repulsive forces between DNA chains (extending to near 60 Å for salt-free complexes, consistent with recent theory (Bruinsma, 1998; Bruinsma and Mashl, 1998)), the DNA molecules homogeneously cover all the available membrane surface (Radler et al., 1997; Salditt et al., 1997, 1998).

This allows us to assume that lipid dynamics is equivalent over the whole CL-DNA surface and therefore the results obtained here may be homogeneously attributed to the total membrane complex.

Whereas, as confirmed by the literature, no modification of the d spacing is observed on DNA addition even at a concentration crossing the isoelectric point (indicating that DNA remains tightly bound to lipid bilayers), the dynamical behavior of the charge neutral CL-DNA complex investigated by neutron scattering is peculiar. Indeed, charge neutralization seems to be accompanied by (or to induce) a strong effect on the lipid motion. In particular, significant anisotropies are responsible for the large differences observed in the thermodynamic parameters characterizing the interconversion between large and small amplitude cages (Fig. 7), where relative variations in the range of 50–65% are observed (δ(ΔH)/H = 51%, δ(ΔS)/S = 65%, δ(ΔG)/G = 65%). It is worth underlining that this increased mobility exclusively involves the out-of-plane motion of the CL-DNA at the isoelectric point, whereas the parameters of the in-plane component remain almost unchanged (except for a very small change in the enthalpic contribution) (Figs. 6–8, solid circles). DNA complexation, on charge neutralization, thus seems to favor the population of the high amplitude motion cage in the out-of-plane configuration, where, on the other hand, the mobility is reduced with respect to the same cages of the other samples, as suggested by the force constant k2. We mention here that k1 and k2 are the force constants associated with the small and large conformational cage (or fluctuations), respectively, and k3 is the force constant at 300 K. This is in agreement with a possible scenario in which the neutral DOPC lipids, due to the acquired higher fluidity of the apolar region and to the charge balance of the lipoplex, with consequent displacement of bound water molecules, may fluctuate more easily in the interlayer free-space (reflecting the increase of the population of the large amplitude motions cage, associated with ΔG and a shift of dynamical transition temperature T0 toward lower values). On the other hand the more compact structure assigned to the neutral complex may be responsible for the reduced dimension of protons movements compared with the other compositions. The cationic lipids are instead assumed to remain localized close to the DNA to balance the total charge. On the other hand, the enhanced disordered conformation in the lipid chains should affect also the chain defect motions. However, this contribution to the observed change in membrane dynamics is assumed to be negligible because it should present projections in both the in-plane and out-of-plane directions, which were not observed experimentally (no appreciable variation of the in-plane dynamics is attributed to DNA addition).

Moving away from the isoelectric point, unlike the invariant lamellar repeat distance d, the DNA chains distance dDNA was observed in SAXS experiments to shift toward lower values for ρ < 2.2 and higher ones for ρ >2.2 (Koltover et al., 1999). Furthermore, measurements of the complex ξ-potential (the electrostatic potential near the membrane surface), show charge reversal at ρ = 2.2 from negative at ρ < 2.2 to positive at ρ > 2.2.

On the other hand, from the dynamical point of view, no differences are observed between the in-plane and out-of-plane lipid motions (Figs. 6–8), and thermodynamic values remain unchanged with respect to the other DNA concentrations. This suggests that the addition of small concentrations of negative DNA phosphate groups is not sufficient to compete with the constraints of unbalanced electrostatic repulsion between the positively charged bilayers and the residual interlayer water molecules. Thus, the CLs-DNA complex at ρ < ρISO does not exhibit any change in lipid motion.

In summary, the balancing of the net charge of the DNA-lipoplex seems to change not only the equilibrium between the populations of the low and the high amplitude motion cages, favoring the crossover at lower temperatures, but also the force constants and therefore the atomic displacements characteristic of the high amplitude motion cage.

CONCLUSIONS

The exceptional combination of spontaneous lamellar phase formation and the feasibility of direction sensitive experiments with neutron scattering allowed us to obtain very important information on the effect of lipid-DNA interaction in the in-plane and out-of-plane lipid motions.

In particular, our results show that a minimum number of DNA phosphate groups do not induce significant modifications in membrane dynamics. On the contrary, at the isoelectric point, the balance of the total net charge inside the complex, together with the displacement of bound water molecules into solution (with counterion release), provides new degrees of freedom for the lipoplex. This determines an increase in apolar region fluidity and in out-of-plane lipid motions, mainly assigned to spatially confined vertical translation of the entire lipid molecule.

Acknowledgments

We thank Dr. Dominique Bicout for stimulating discussions on the model used for data treatment.

References

  1. Bandyopadhyay, S., M. Tarek, and M. L. Klein. 1999. Molecular dynamics study of a lipid-DNA complex. J. Phys. Chem. B. 103:10075–10080. [Google Scholar]
  2. Bée, M. 1998. Quasielastic Neutron Scattering: principles and applications in solid state chemistry, biology and material science. Adam Hilger, Bristol, UK.
  3. Bicout, D. J., and G. Zaccai. 2001. Protein flexibility from the dynamical transition: a force constant analysis. Biophys. J. 80:1115–1123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Braun, C. S., G. S. Jas, S. Choosakoonkriang, G. S. Koe, J. G. Smith, and C. R. Middaugh. 2003. The structure of DNA within cationic lipid/DNA complexes. Biophys. J. 84:1114–1123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bruinsma, R. F. 1998. Electrostatics of DNA-cationic lipid complexes: isoelectric instability. Eur. Phys. J. B. 4:75–88. [Google Scholar]
  6. Bruinsma, R. F., and J. Mashl. 1998. Long-range electrostatic interaction in cationic-lipid complexes. Europhys. Lett. 41:165–168. [Google Scholar]
  7. Caracciolo, G., R. Caminiti, F. Natali, and A. Congiu Castellano. 2002a. A new approach for the study of cationic lipid-DNA complexes by energy dispersive x-ray diffraction. Chem. Phys. Lett. 366:200–204. [Google Scholar]
  8. Caracciolo, G., R. Caminiti, D. Pozzi, M. Friello, F. Boffi, and A. Congiu Castellano. 2002b. Self-assembly of cationic liposomes-DNA complexes: a structural and thermodinamic study by EDXD. Chem. Phys. Lett. 351:222–228. [Google Scholar]
  9. Caracciolo, G., D. Pozzi, R. Caminiti, and A. Congiu Castellano. 2003. Structural characterization of a new lipid/DNA complex showing a selective transfection efficiency in ovarian cancer cells. Eur. Phys. J. E. 10:331–336. [DOI] [PubMed] [Google Scholar]
  10. Choosakoonkriang, S., C. M. Wiethoff, T. J. Anchordoquy, G. S. Koe, J. G. Smith, and C. R. Middaugh. 2001. Infrared spectroscopic characterization of the interaction of cationic lipids with plasmid DNA. J. Biol. Chem. 276:8037–8043. [DOI] [PubMed] [Google Scholar]
  11. Crook, K., B. J. Stevenson, M. Dubouchet, and D. J. Porteous. 1998. Inclusion of cholesterol in DOTAP transfection complexes increases the delivery of DNA to cells in vitro in the presence of serum. Gene Ther. 5:137–143. [DOI] [PubMed] [Google Scholar]
  12. Cullis, P. R., and B. de Kruijff. 1979. Lipid polymorphism and the functional roles of lipids in biological membranes. Biochim. Biophys. Acta. 559:399–420. [DOI] [PubMed] [Google Scholar]
  13. Deriu, A. 1993. The power of quasielastic neutron scattering to probe biophysical systems. Phys. Rev. B. 183:331–342 [Google Scholar]
  14. Doster, W., S. Cusack, and W. Petry. 1989. Dynamical transition of myoglobin revealed by inelastic neutron scattering. Nature. 337:754–756. [DOI] [PubMed] [Google Scholar]
  15. Essmann, U., and M. X. Berkowitz. 1999. Dynamical properties of phospholipid bilayers from computer simulation. Biophys. J. 76:2081–2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Farhood, H., N. Serbina, and L. Huang. 1995. The role of dioleoyl phosphatidylethanolamine in cationic liposome mediated gene transfer. Biochim. Biophys. Acta. 1235:289–295. [DOI] [PubMed] [Google Scholar]
  17. Felgner, P. L., T. R. Gadek, M. Holm, R. Roman, H. W. Chan, M. Wenz, J. P. Northrop, G. M. Ringold, and M. Danielsen. 1987. Lipofection: a highly efficient, lipid-mediated DNA-transfection procedure. Proc. Natl. Acad. Sci. USA. 84:7413–7417. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Friedmann, T. 1997. Overcoming obstacles to gene therapy. Sci. Am. 276:96–101. [PubMed] [Google Scholar]
  19. Harries, D., S. May, W. Gelbart, and A. B. Shaul. 1998. Structure, stability, and thermodynamics of lamellar DNA-lipid complexes. Biophys. J. 75:159–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hirsch-Lerner, D., and Y. Barenholz. 1999. Hydration of lipoplexes commonly used in gene delivery: follow-up by laurdan fluorescence changes and quantification by differential scanning calorimetry. Biochim. Biophys. Acta. 1461:47–57. [DOI] [PubMed] [Google Scholar]
  21. Kennedy, M. T., E. V. Pozharski, V. A. Rakhmanova, and R. C. MacDonanld. 2000. Factors governing the assembly of cationic phospholipid-DNA complexes. Biophys. J. 78:1620–1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Koltover, I., T. Salditt, and C. R. Safinya. 1999. Phase diagram, stability, and overcharging of lamellar cationic lipid-DNA self-assembled complexes. Biophys. J. 77:915–924. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Koltover, I., K. Wagner, and C. R. Safinya. 2000. DNA condensation in two dimensions. Proc. Natl. Acad. Sci. USA. 97:14046–14051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. König, S., W. Pfeiffer, T. Bayerl, D. Richter, and E. Sackmann. 1992. Molecular dynamics of lipid bilayers studied by incoherent quasi-elastic neutron scattering. J. Phys. II France. 2:1589–1615. [Google Scholar]
  25. Lin, A. J., N. L. Slack, A. Ahmad, C. X. George, C. E. Samuel, and C. R. Safinya. 2003. Three-dimensional imaging of lipid gene-carriers: membrane charge density controls universal transfection behavior in lamellar cationic liposome-DNA complexes. Biophys. J. 84:3307–3316. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Liu, Y., L. C. Mounkes, H. D. Liggitt, C. S. Brown, I. Solodin, T. D. Heath, and R. J. Debs. 1997. Factors influencing the efficiency of cationic liposome-mediated intravenous gene delivery. Nat. Biotechnol. 15:167–173. [DOI] [PubMed] [Google Scholar]
  27. Manning, G. S. 1969. Limiting laws and counterion condensation in polyelectrolyte solutions. I. Colligative properties. J. Chem. Phys. 51:924–933. [Google Scholar]
  28. Natali, F., A. Gliozzi, R. Rolandi, A. Relini, P. Cavatorta, A. Deriu, A. Fasano, and P. Riccio. 2002. Myelin basic protein reduces molecular motions in DMPA, an elastic neutron scattering study. App. Phys. A. Mat. Sci. & Proc. 74:s1582–s1584. [Google Scholar]
  29. Natali, F., A. Gliozzi, R. Rolandi, A. Relini, P. Cavatorta, A. Deriu, A. Fasano, and P. Riccio. 2003. Protein-membrane interaction: effect of myelin basic protein on the dynamics of oriented lipids. Chem. Phys. 292:455–464. [Google Scholar]
  30. Natali, F., A. Gliozzi, R. Rolandi, A. Relini, P. Cavatorta, A. Deriu, P. Riccio, and A. Fasano. 2000. Myelin basic protein reduces molecular motions in DMPA, an elastic neutron scattering study. Physica B. 301:145–149. [Google Scholar]
  31. Radler, J. O., I. Koltover, T. Salditt, and C. R. Safinya. 1997. Structure of DNA-cationic liposome complexes: DNA intercalation in multilamellar membranes in distinct interhelical packing regimes. Science. 275:810–814. [DOI] [PubMed] [Google Scholar]
  32. Reat, V., G. Zaccai, M. Ferrand, and C. Pfister. 1997. Functional dynamics in purple membrane. In Biological Macromolecular Dynamics. S. Cusack, H. Büttner, M. Ferrand, P. Langan, and P Timmins, editors. Adenine Press, Schenectady, NY. 117–121.
  33. Regelin, A. E., S. Fankhaenel, L. Gurtesch, C. Prinz, G. von Kiedrowski, and U. Massing. 2000. Biophysical and lipofection studies of DOTAP analogs. Biochim. Biophys. Acta. 1464:151–164. [DOI] [PubMed] [Google Scholar]
  34. Roux, D., and C. R. Safinya. 1988. A synchrotron x-ray study of competing undulation and electrostatic interlayer interactions in fluid multimembrane lyotropic phases. J. Phys. France. 49:307–313. [Google Scholar]
  35. Rubanyi, G. M. 2001. The future of human gene therapy. Mol. Aspects Med. 22:113–142. [DOI] [PubMed] [Google Scholar]
  36. Safinya, C. R. 1989. Rigid and fluctuating surfaces: a series of synchrotron x-ray scattering studies of interacting stacked membranes. In Phase Transition in Soft Condensed Matter. T. Riste and D. Sherrington, editors. Nato ASI Series B. 211:249–270.
  37. Safinya, C. R. 2001. Structures of lipid-DNA complexes: supramolecular assembly and gene delivery. Curr Opin. Struct. Biol. 11:440–448. [DOI] [PubMed] [Google Scholar]
  38. Saiz, L., and M. L. Klein. 2002a. Electrostatic interactions in a neutral model phospholipid bilayer by molecular dynamics simulations. J. Chem. Phys. 116:3052–3057. [Google Scholar]
  39. Saiz, L., and M. L. Klein. 2002b. Computer simulation studies of model biological membranes. Acc. Chem. Res. 35:482–489. [DOI] [PubMed] [Google Scholar]
  40. Salditt, T., I. Koltover, J. O. Radler, and C. R. Safinya. 1997. Two-dimensional smectic ordering of linear DNA chains in self-assembled DNA-cationic liposome mixtures. Phys. Rev. Lett. 79:2582–2585. [Google Scholar]
  41. Salditt, T., I. Koltover, J. O. Radler, and C. R. Safinya. 1998. Self-assembled DNA–cationic-lipid complexes: Two-dimensional smectic ordering, correlations, and interactions. Phys. Rev. E. 58:889–904. [Google Scholar]
  42. Squires, G. L. 1997. Introduction to the Theory of Thermal Neutron Scattering. Dover, London.
  43. Wong, G. C. L., J. X. Tang, A. Lin, Y. Li, P. A. Janmey, and C. R. Safinya. 2000. Hierarchical self-assembly of F-actine and cationic lipid complexes: stacked three-layer tubule networks. Science. 288:2035–2039. [DOI] [PubMed] [Google Scholar]
  44. Zaccai, G. 2000. How soft is a protein? A protein dynamics force constant measured by neutron scattering. Science. 288:1604–1607. [DOI] [PubMed] [Google Scholar]
  45. Zuhorn, I. S., V. Oberle, W. H. Visser, J. B. F. N. Engberts, U. Bakowsky, E. Polushkin, and D. Hoechkstra. 2002. Phase behavior of cationic amphiphiles and their mixtures with helper lipid influences lipoplex shape, DNA translocation, and transfection efficiency. Biophys. J. 83:2096–2108. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES