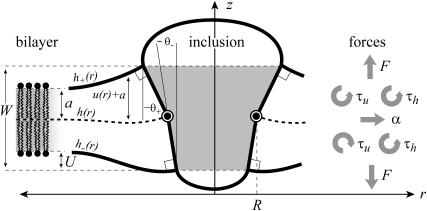
FIGURE 1.

A schematic picture of the bilayer-inclusion model. The geometry of the inclusion is described by four parameters: the radius R, the thickness W, and the radial slopes H′± of the top and bottom surfaces of the bilayer, respectively. If the surfaces of the bilayer are locally normal to the interface of the inclusion, as depicted above, H′± = θ± in the small-angle approximation. The bilayer equilibrium thickness is 2a. The fields h ± (r) are the z displacements of the top and bottom surfaces of the bilayer, respectively. Their average is the midplane displacement, h(r), and half their difference is u(r) + a. The value u(r) is the local thickness deformation of a single leaflet of the bilayer. At the interface, twice this deformation, 2U, is the hydrophobic mismatch, W − 2a. The generalized forces on the inclusion induced by the bilayer are depicted for positive values. F is the expansion-compression force, α is the tension, τ_h is the midplane torque, and τ_u is the shape torque.