Molecular Dynamics Simulations Indicate a Possible Role of Parallel β-Helices in Seeded Aggregation of Poly-Gln

Abstract

The molecular structures of amyloid fibers characterizing neurodegenerative diseases such as Huntington's or transmissible spongiform encephalopathies are unknown. Recently, x-ray diffraction patterns of poly-Gln fibers and electron microscopy images of two-dimensional crystals formed from building blocks of prion rods have suggested that the corresponding amyloid fibers are generated by the aggregation of parallel β-helices. To explore this intriguing concept, we study the stability of small β-helices in aqueous solution by molecular dynamics simulations. In particular, for the Huntington aggregation nucleus, which is thought to be formed of poly-Gln polymers, we show that three-coiled β-helices are unstable at the suggested circular geometries and stable at a triangular shape with 18 residues per coil. Moreover, we demonstrate that individually unstable two-coiled triangular poly-Gln β-helices become stabilized upon dimerization, suggesting that seeded aggregation of Huntington amyloids requires dimers of at least 36 Gln repeats (or monomers of ∼54 Gln) for the formation of sufficiently stable aggregation nuclei. An analysis of our results and of sequences occurring in native β-helices leads us to the proposal of a revised model for the PrP^Sc aggregation nucleus.

INTRODUCTION

Amyloid fibers are β-sheet-rich, large, and insoluble aggregates of peptides or proteins. Deposition of such aggregates in the brain is the pathological hallmark of common neurodegenerative diseases. The deposits and smaller aggregation intermediates appear to be involved in the pathogenesis of neuronal cell death (Caughey and Lansbury, 2003). Because the fibers are large and hard to crystallize, high-resolution structural analysis is severely hampered. In addition, it is notoriously difficult to stabilize aggregation intermediates for this purpose.

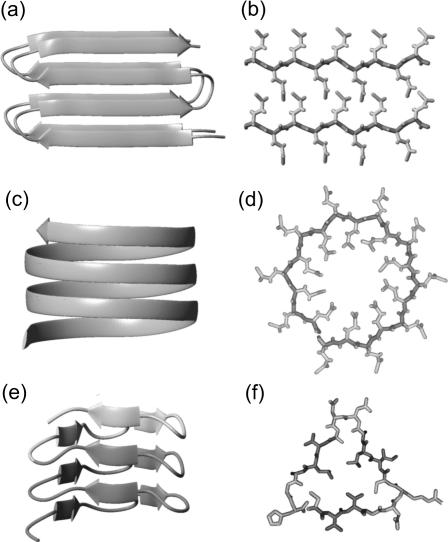
Although the peptides forming amyloid fibers exhibit little or no sequence similarity, the fibers are assumed to have common structural motifs (Sunde et al., 1997). The aggregation is supposed to proceed through a structural conversion and oligomerization leading to an ordered aggregation nucleus, which initiates fiber growth (Rochet and Lansbury, 2000). In x-ray diffraction many fibers show the so-called cross-β pattern, which is characterized by a sharp 4.75-Å meridional and a broader 10-Å equatorial reflection (Sunde and Blake, 1998). Fig. 1, a and b, depicts a sample structure that fits to such a pattern. Here, stacks of antiparallel β-sheets form a hydrogen-bonded aggregate along the fiber axis. The meridional 4.75-Å reflection is due to the spacing between the main chains of the hydrogen-bonded β-strands (Fig. 1 a). For the given example, the equatorial 10-Å reflection is due to the parallel stacking of the backbone in the cross section of the fiber visible in Fig. 1 b. Note that the cross-β pattern is also compatible with double-layered β-strands aggregating through in-register parallel β-sheet formation along the fiber axis as suggested by Petkova et al. (2002) for Aβ_1–40 on the basis of solid-state NMR-data.

FIGURE 1.

Model of stacked antiparallel β-sheets corresponding to a cross-β x-ray pattern (a and b), as well as structures of a circular (c and d) and a triangular (e and f) parallel β-helix with 20 and 18 residues per helical coil, respectively. The β-helices are compatible with the absence of the 10-Å reflection. The circular model visualizes a suggestion by Perutz et al. (2002a) for the building blocks of poly-Gln amyloid fibers. The triangular structure is a three-coiled fragment of a native left-handed β-helix in the enzyme LpxA (Raetz and Roderick, 1995) (residues 125–179); dark shaded marks a two-coiled fragment. (a, c, and e) Side views. (b, d, and f) Cross sections; in the cross-section f covering the residues 127–144, three β-strands (dark shaded) are separated by turns (light shaded).

However, the 10-Å reflection is absent or very weak in x-ray diffraction patterns of amyloid fibers associated with Huntington's disease and with particular fragments of the Alzheimer Aβ peptide (Perutz et al., 2002a). Perutz et al. (2002a) have focused on the structure of these fibers. Also here, a strong meridional reflection at 4.75 Å indicates that β-sheets must be oriented perpendicular to the fiber axis. On the other hand, the absence of the 10-Å reflections shows that the backbone cannot exhibit a parallel stacking. Instead, a circular β-helix (Fig. 1 c) as well as other shapes (Jenkins and Pickersgill, 2001) of parallel β-helices (like the one in Fig. 1 e) are compatible with such a diffraction pattern.

As a particular example, Perutz et al. (2002a) have interpreted the x-ray diffraction patterns of fibers aggregated from short poly-L-Gln peptides D₂Q₁₅K₂ in terms of a model, according to which the fibers have a diameter of ∼3 nm and are made up of circular β-sheets. This example is important, because Huntington's disease, like other related neurodegenerative diseases, is caused by large (≥35) Gln repeats (Ross et al., 2003). Furthermore, fibers formed by an exon-1 protein of huntingtin, which contains a 51-Gln repeat, exhibit similar x-ray diffraction patterns (Perutz et al., 2002b). These and other facts have led Perutz et al. (2002a) to speculate that the poly-Gln segments directly promote the growth of the respective amyloid fibers and provide the required building blocks in the form of at least two coils of circular parallel β-helices comprising 18 or 20 residues each (Perutz et al., 2002a). (Adopting the nomenclature suggested by Jenkins and Pickersgill (2001), we call a complete turn of a parallel β-helix a coil.) Fig. 1, c and d, shows a three-coiled sample structure constructed according to the suggestion of Perutz et al. (2002a) for 55 and 61 poly-Gln repeats. In these circular parallel β-helices the side chains point alternatingly into and out of the fiber axis. Note that the cylindrical structures, which were suggested by Perutz et al. (2002a) to be formed from these β-helical building blocks and to represent the core motif for huntingtin aggregation, do not exactly match any of the native parallel β-helical structures classified by Jenkins and Pickersgill (2001).

At the same time, a parallel β-helix motif has also been proposed by Wille et al. (2002) for scrapie prion. According to these authors, among the known secondary structural motifs only parallel β-helices appeared to be compatible with electron microscopy images of two-dimensional crystals formed from building blocks of prion rods.

This unusual secondary structure motif is known from several protein families in which left- and right-handed β-helices are found (Jenkins and Pickersgill, 2001). Many left-handed β-helices resemble an equilateral prism as in the case of UDP-N-acetylglucosamine acyltransferase (LpxA) (Raetz and Roderick, 1995), contain 18 residues per helical coil, and occasionally exhibit interruptions of the helical coils by loop structures. Fig. 1 e depicts a three-coiled β-helical fragment of LpxA and Fig. 1 f one of its helical coils. It consists of three β-strands linked by turns. Six of the 18 side groups are oriented toward the core of the helix, which is densely packed with hydrophobic or weakly polar residues (Raetz and Roderick, 1995). In contrast, the sequences and shapes of right-handed β-helices are less regular, and the sizes of their helical coils are larger (Jenkins and Pickersgill, 2001). Whereas all these proteins avoid aggregation by capping the β-helices (Richardson and Richardson, 2002), an isolated β-helix domain of the P22 tailspike protein quickly aggregates into amyloid-like fibers by linear polymerization (Schuler et al., 1999). To explain the corresponding data the parallel β-helix has been speculated to provide the structural motif of fiber growth (Schuler et al., 1999).

One may ask whether, and how, one can substantiate or reject the quoted speculations on the structure of amyloid fibers. Here, we claim that molecular dynamics (MD) simulations (van Gunsteren and Berendsen, 1990) can provide additional evidence, because they can provide measures for the stability of suggested building blocks.

Processes of protein folding and aggregation sensitively depend on the thermodynamic conditions and on a subtle balance of the electrostatic interactions within the protein-solvent system (Warshel and Russell, 1984) which, therefore, have to be adequately represented in MD simulations (Tavan et al., 2005). To generate a well-defined thermodynamic ensemble in MD, one has to enclose the protein and a small (3- to 8-nm) neighborhood of solvent molecules by periodic boundaries (Allen and Tildesley, 1987). For an adequate treatment of the electrostatic interactions one has to apply either Ewald (Frenkel and Smit, 2002) or moving-boundary reaction-field techniques (Mathias et al., 2003; Mathias and Tavan, 2005).

MD simulations of protein-solvent systems comprising 10⁴–10⁵ atoms are time-consuming. Therefore, they are currently limited to small peptides (like those shown in Fig. 1) in solution and to processes occurring within ∼10 ns. Nevertheless, the accessible timescale should be long enough to investigate the stability of selected and predefined β-helical peptide structures. If a small model structure, like the one depicted in Fig. 1 c, should dissolve within nanoseconds upon simulation of its thermal motion in aqueous solution, then the current MD simulation techniques (Mathias et al., 2003, Lindahl et al., 2001) should be reliable enough (Ponder and Case, 2003) to allow the prediction that this structure is thermodynamically unstable. In processes of amyloid fiber formation such a lack of short-time stability is important, because a correspondingly flexible monomeric structure cannot serve as a template and nucleus for aggregation. Conversely, if a suggested structure does not decay within 10 ns of MD simulation, this may be taken as an indication of its metastability (because it cannot be excluded that it will decay at longer timescales) and, therefore, of its being a candidate nucleus for aggregation. The latter evidence can then be strengthened, if the metastability becomes more pronounced upon a rise of temperature or upon oligomerization. We hold this optimistic view on the capabilities of MD simulations, despite the serious deficiencies of the available molecular mechanics (MM) force fields (particularly concerning the neglect of the electronic polarizability (Ponder and Case, 2003)). Of course, the working hypothesis outlined above has to be validated by first considering β-helical sample structures, whose stabilities can be a priori estimated from general arguments.

Adopting this MD-based testing scenario, we want to check the suggestion of Perutz et al. (2002a) according to which the poly-Gln aggregation nuclei are circular β-helices (cf. Fig. 1 c) aggregating into water-filled nanotubes. Here we will exclude from consideration the short D₂Q₁₅K₂ model peptides, which according to Perutz et al. form circles aggregating into cylinders, because the extremely slow kinetics of their seeded aggregation (Chen et al., 2001) indicates the necessity of forming large oligomers for nucleation in this case. Instead we will consider larger Gln polymers comprising at least 37 residues, because for such peptides the aggregation kinetics becomes much faster (Chen et al., 2001). Our decision to study Gln polymers is additionally motivated by the fact that they pose no difficulties in matching a sequence onto a structural model. We have selected left-handed β-helices, because they exhibit a smaller variability of shape, size, and sequence than the right-handed β-helices and occur at smaller sizes of the helical coils. These sizes are compatible with the 3-nm diameter determined by Perutz et al. (2002a) for their poly-Gln fibers. Therefore, we will model the circular β-helices suggested by these authors as left-handed.

A related MD study also aiming at a stability assessment of amyloid structural motifs has been presented by Ma and Nussinov (2002a,b). These authors have studied stacks of β-sheets like those depicted in Fig. 1, a and b, for alanine-rich peptides and sequence portions of the Alzheimer Aβ-peptide.

METHODS

To construct a supposedly stable β-helix model, we selected two and three regularly shaped coils from LpxA (entry 1LXA (Berman et al., 2000) of the Protein Data Bank) as depicted in Fig. 1 e and characterized in the figure caption. These β-helical fragments start and terminate at locations within the turns, because many native β-helices start, end, or are interrupted by loops at turn positions. By acetylating (Ac) the N- and amidating (NH₂) the C-terminus, we avoid terminal charges and emulate the fragments as parts of the native β-helix.

Triangular three-coiled models were built by matching poly-Ala, poly-Gln, poly-Ser, and poly-Ile sequences onto the structure of the native LpxA fragment. For poly-Gln an additional two-coiled triangular structure was modeled. A dimer was formed by arranging two of these structures into an overall four-coiled β-helix. To achieve a close fit, here, the two-coiled monomers were restricted to 36 glutamines by omitting the N-terminal residue.

Circular poly-Gln tubes with 18 and 20 residues per coil (cf. Fig. 1 c) were built with InsightII (Accelrys, San Diego, CA) in the suggested dimensions (Perutz et al., 2002a). Starting from planar poly-Gln β-sheets with 55 and 61 residues, respectively, the peptides were bent into circles by modifying the angles between the C_α atoms. Stretching the resulting circular β-helix into the axial direction rendered the 4.75 Å helical pitch.

MD simulations

As our simulation system we chose a periodic rhombic dodecahedron large enough to enclose a sphere with a radius of 34 Å. Initially, this system was filled with 7813 water molecules modeled by the CHARMM variant of the TIP3P potential (Jorgensen et al., 1983; MacKerell et al., 1998) because the parameters of the peptide force field were also adopted from CHARMM22 (MacKerell et al., 1998).

All simulations were carried out in the NpT ensemble with the program package EGO-MMII (Mathias et al., 2003). The temperature T and the pressure p were controlled by a thermostat (τ = 0.1 ps) and a barostat (τ = 1.0 ps, β = 5.0 Pa) (Berendsen et al., 1984). Covalent bonds of hydrogen atoms were kept fixed using M-SHAKE (Kräutler et al., 2001). The integration time step was 2 fs.

The long-range Coulomb interactions were treated by a particular combination of structure-adapted multipole expansions (Niedermeier and Tavan, 1994) with a moving-boundary reaction-field approach and a multiple time-step integrator (Mathias et al., 2003, Mathias and Tavan, 2004). Van der Waals interactions were calculated explicitly up to 10.5 Å; at larger distances a mean field approach (Allen and Tildesley, 1987) was applied.

For solvation, the peptides were positioned at the center of the equilibrated (1 ns, T = 300 K, p = 1.013 × 10⁵ Pa) water box and all water molecules <2.0 Å from a peptide atom were removed. For equilibration the peptides initially were kept fixed, whereas the surrounding solvent molecules were thermally moving for several hundred picoseconds at T = 500 K and T = 300 K. Next, the rigid constraints were removed and solely the positions of the peptide C_α atoms were constrained by harmonic potentials (force constant 2.1 × 10² kJ/(mol·Å²)). By energy minimization these systems were cooled within 1 ps to below T = 0.1 K and subsequently heated within 120 ps to T = 300 K. Within another 300 ps the constraining force constants were slowly reduced to zero until the peptides were free to move within the solvent. This procedure served to adjust the modeled peptide structures to the MM force field or, equivalently, to partially remove the prejudices imposed on the structures by the modeling. The simulation systems thus obtained were the starting points for the following unconstrained 2- to 10-ns simulations at T = 300 K and p = 1.013 × 10⁵ Pa (coordinates saved every 0.2 ps).

Measures for structural stability

Initial structures of the various coils j, j = 1, …, M, within an M-coiled β-helix, were obtained as averages over the time interval from 100 ps to 400 ps of the unconstrained simulations. The subsequently sampled MD structures were matched onto the respective initial structures by least-square fits using the positions of the C_α atoms. The resulting root mean-square deviations 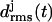were taken as measures of the structural stabilities of the coils j. To judge the overall stability of a β-helical peptide containing M coils, the average value 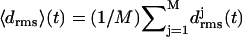of the coil-specific deviations 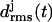was calculated.

A huge number of further observations covering empirical measures for secondary-structure content, hydrogen bonding, simulated (Φ, Ψ) dihedral-angle distributions, and deviations of these dihedral angles from their initial values has also been calculated for cross-checking conclusions derived from the coil-specific and coil-average Cartesian root mean-square deviations. However, in this article we will not include this huge amount of data, which can be extracted from the virtual reality of MD simulations, because we want to save space and avoid an overstretching of the reader's patience. Images of the peptides were created with the molecular graphics program MOLMOL (Koradi et al., 1996).

RESULTS AND DISCUSSION

The well-known deficiencies of the current nonpolarizable MM force fields (Ponder and Case, 2003), which are shared by the force field employed by us (MacKerell et al., 1998), generally preclude reliable predictions of peptide structures by MD simulation. Nevertheless, one can expect that natively stable peptide secondary structures, such as α-helices or β-sheets, at least represent local minima of the free-energy landscape generated by such a force field. If this is the case, the corresponding peptide conformations represent metastable states and in short-time simulations their metastability shows up as a conformational invariance for a certain time span. The average size of this time span is determined by the minimal height of the free energy barriers surrounding the given local minimum or, equivalently, by the depth of that minimum.

If one starts an MD simulation with a peptide structure, which is close to a metastable conformation in configuration space, one expects only slight structural rearrangements of the given starting structure, because it will rapidly relax toward that metastable state. On the other hand, if a starting structure is far away from a metastable conformation, it will become rapidly and strongly distorted.

In this study, we apply the method of MD simulation to a secondary structure motif, the left-handed parallel β-helix, which, to our best knowledge, has not yet been treated by MD simulation before. Therefore, to judge the stabilities of our peptide structures in solution, we first have to construct a stability scale. To this aim we will use simulation results on structures, for which we a priori expect grossly different stabilities from general arguments.

Stability scale

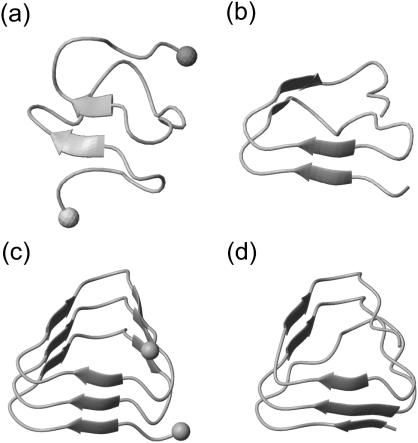
According to the above arguments, natively stable β-helices should show signs of structural stability also in our nanosecond MD simulations. To check whether this is actually the case and how stability is monitored by MD, we first consider the two- (dark shaded) and three-coiled fragments (dark and light shaded) of the LpxA helix depicted in Fig. 1 e.

In solution the stability of such a fragment will decrease, if it has charged N- and C termini, because the charged ends will be drawn into the solvent. Thus, such a fragment will be artificially destabilized as compared to the native situation. To check as to whether this effect shows up in our short-time simulations, we have simulated the LpxA fragments with charged and with neutralized ends, respectively, at 300 K for 2 ns starting from the structures shown in Fig. 1 e.

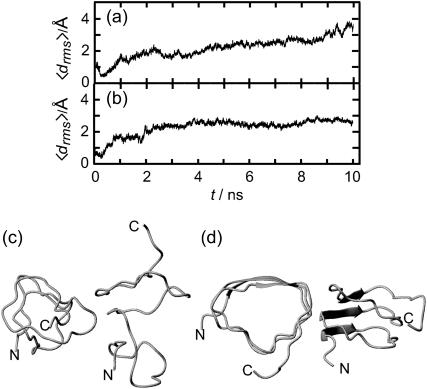
Fig. 2, a and b, compares the two-coiled structures observed after 2-ns simulation. Fig. 2 a demonstrates that the solvation of the charged termini is complete after this short time span and has broken up the β-sheet hydrogen bonds in a zipper-like fashion. In contrast, the 2-ns structure of the fragment with neutral termini shown in Fig. 2 b still resembles the starting structure (cf. Fig. 1 e, dark shaded), if one disregards a small conformational transition at one of the turns within the N-terminal coil 1.

FIGURE 2.

Snapshots of LpxA fragments after 2 ns of MD simulation: two coils (a) with charged N- and C-termini marked by spheres, and (b) with neutral termini; three coils (c) with charged termini (spheres), and (d) with neutral termini.

Thus, the simple two-coiled example of a native β-helical fragment has shown that the destabilizing solvation effect induced by charged ends is strong enough to be observable within a short (2-ns) MD simulation. On the other hand, one may also expect that the depth of the local free-energy minimum corresponding to a fragment of natively stable structure will increase with the size of that fragment. Therefore, the question arises whether short-time simulations can catch also this stabilizing effect counteracting the destabilization induced by the solvation tendency of the charged ends.

For an answer consider Fig. 2, c and d, which compares the 2-ns structures of the three-coiled models obtained for charged and neutral ends, respectively. Apart from very small conformational changes near the termini, the starting structure is preserved in both models. Thus, the stabilization induced by the additional coil sufficiently deepens the local free energy minimum of the native conformation and prevents a thermally activated escape within 2 ns independently of the destabilizing charge solvation effect.

Because we want to evaluate the stability of smallβ-helical structures undisturbed by these solvation effects we have generally modeled the fragments of the native LpxA as well as the other β-helical peptides described in Methods with neutral, i.e., acetylated and amidated, termini. To check whether the asserted stability of the two-coiled LpxA fragment (neutral ends) pertains to longer time spans than the 2 ns discussed above, we have simulated its dynamics for another 2 ns.

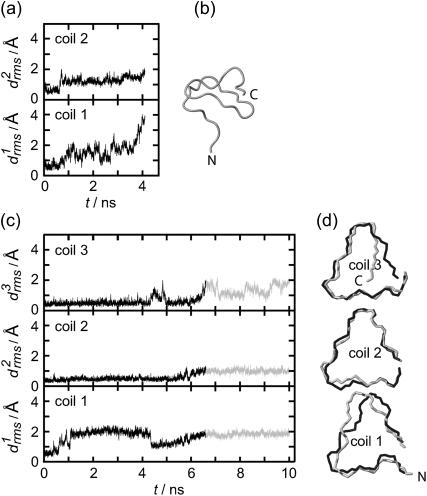
According to Fig. 3 a, the root mean-square deviations 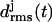increase at both coils, j = 1, 2, after ∼1 ns (see Methods for the definition of 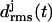). This increase reflects the conformational change at one of the turns, which we have already mentioned in connection with Fig. 2 b. The additional strong increase of 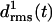after 3 ns is caused by a loosening of the N-terminus, which is apparent in the 4-ns structural snapshot depicted in Fig. 3 b.

FIGURE 3.

Temporal evolution of the root mean-square deviations 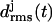of the various coils j in MD simulations of two- (a) and three-coiled (c) LpxA fragments. Coils are numbered starting at the N-terminus. (b) Snapshot of the two-coiled fragment after 4 ns. (c) Two simulation periods marking different conformations (black and light shaded) of the three-coiled fragment are distinguished in the plots of 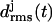. (d) Average structures of the three coils for the black and light shaded periods.

As a result, the interaction between two coils is apparently too weak to keep a hydrated two-coiled fragment of a native β-helix stable within a 4 ns MD simulation. Therefore we checked, whether adding a third coil suffices to stabilize the native structure for 4 ns or longer.

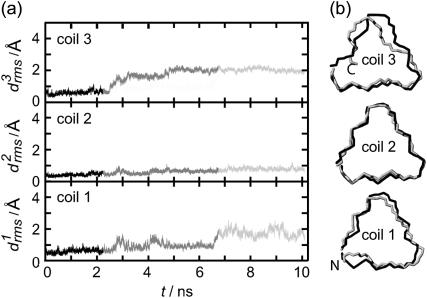
Fig. 3 c shows the 10-ns evolution of the 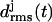values for the three LpxA coils (cf. Fig. 1 e). At the coils j = 2, 3 the 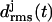values remain small for ∼6.5 ns, indicating that these coils keep their respective initial conformations. Visual inspection of the structures of the N-terminal coil 1 reveals that the increase of 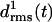at ∼1 ns is caused by a small conformational change at one of the turns, which is similar to the one noted above for the two-coiled structure (data not shown). As demonstrated by the average structures of the coils during the first 6.5 ns (drawn in black in Fig. 3 d), the fragment remains essentially stable within this time span. At 6.5 ns the concomitant rise of all three 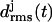indicates a conformational change whose nature becomes apparent by comparison of the light shaded (averages over the last 3.5 ns) and black structures in Fig. 3 d. Accordingly, the conformational change is confined to the top and bottom coils of the fragment, whereas the central coil remains nearly unchanged.

As a result, the three-coiled fragment of LpxA is much more stable than the two-coiled fragment, and this enhanced stability is particularly pronounced at the central coil, which is sandwiched by the two partially water-exposed coils and, therefore, experiences an approximately native molecular environment. We conclude 1), that a natively stable β-helical coil remains stable for 10 ns in our MD simulations if it is in a native environment, and 2), that the stability of hydrated fragments of a native β-helix increases with the number of coils. Furthermore, the kind of structural stability, which is characterized by the 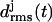curves depicted in Fig. 3 c, defines a stability scale for our MD approach:

Three-coiled β-helix peptides with similar 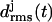curves will be called “stable”, whereas peptides exhibiting a stronger increase of the 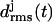values will be classified as “unstable”. This approach relies on the assumption that the MM force field can identify local minima in the free energy landscape, can account for basic physicochemical effects deepening or flattening these minima, and does not require the accuracy necessary for quantitative predictions of thermodynamic stability or of transition rates between metastable states.

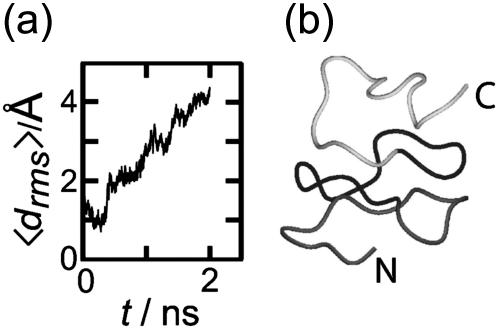
To check the validity of the stability scale defined above, we additionally analyzed a triangular three-coiled poly-Ala β-helix. We a priori expect that this structure is unstable, because poly-Ala peptides preferentially form α-helices (Chakrabartty et al., 1991; Blondelle et al., 1997). Fig. 4 a depicts the evolution of the average deviation 〈d_rms〉(t) of the corresponding coil structures from the initial values (see Methods for the definition of 〈d_rms〉(t)). The deviation 〈d_rms〉(t) rapidly increases within 2 ns to reach a value of 4.4 Å. This value is larger than the corresponding value of 2.8 Å reached for the unstable two-coiled LpxA fragment after 4 ns, and much larger than the 10-ns value of 1.6 Å for the stable three-coiled LpxA fragment. Thus, our stability scale classifies the three-coiled poly-Ala β-helix as “very unstable”. The 2-ns structural snapshot in Fig. 4 b confirms that the poly-Ala peptide is actually decaying toward a random coil.

FIGURE 4.

(a) Average root mean-square deviation of the β-helical coils (cf. Methods) for a three-coiled triangular poly-Ala β-helix during 2 ns of simulation. (b) Snapshot of structure at 2 ns.

This result verifies that our MD-based testing can provide reasonable estimates for the stabilities of small β-helical peptides. Despite the inaccuracies of MM-force fields (Ponder and Case, 2003) it should allow us to reliably judge the stabilities of related β-helical models.

Poly-Gln models

We first address the question of whether the three-coiled circular poly-Gln β-helices containing 18 and 20 residues per coil suggested by Perutz et al. (2002a) are stable. Fig. 5, a and b, shows the corresponding 〈d_rms〉(t) curves obtained from 10-ns simulations. Immediately after the start of the unconstrained simulations, the 〈d_rms〉(t) values steeply increase and reach a value of ∼2 Å at 2 ns, in both cases indicating that the β-helices quickly deviate from their initial circular shapes. The quoted 2-ns value is two times larger than the corresponding 2-ns value of 1.0 Å observed for the stable three-coiled LpxA fragment, and therefore, both circular poly-Gln models are classified as unstable.

FIGURE 5.

Temporal evolution of the 〈d_rms〉(t) values of circular poly-Gln β-helices with 18 (a) and 20 residues (b) per coil. (c and d) Snapshots of the respective structures after 10 ns.

In fact, an analysis of the structures acquired after 2 ns reveals that the circular β-strand coils, in which the Gln residues alternatingly pointed toward and away from the center of the helix, have decayed by partial or complete outward side-chain flips into coil structures now exhibiting partial or complete turns at the respective flip positions. Concomitantly with these fast conformational flips several water molecules initially filling the cores of the circular models were sqeezed out into the aqueous environment or into the region between adjacent coils (data not shown). Correspondingly, the initial conformational relaxation of the two circular models may be described as a beginning hydrophobic collapse and as the breaking of the circular symmetry by introduction of turns and of undistorted β-strands. Beyond 2 ns, the 〈d_rms〉(t) curves of the two circular β-helices start to differ:

For the 18-member coils (cf. Fig. 5 a) the average deviation 〈d_rms〉(t) continues to increase until it reaches a value of 3.7 Å at 10 ns, which is nearly as large as the 2-ns value (4.4 Å) of the very unstable poly-Ala model and by 2.1 Å larger than the 10 ns value of the stable three-coiled LpxA fragment. Therefore, the considered circular poly-Glnβ-helix must be very unstable. This judgment is corroborated by the 10-ns snapshot shown in Fig. 5 c. Instead of the initial circular shape a nearly random coil is seen.

For the 20-member coils, in contrast, the 〈d_rms〉(t) curve in Fig. 5 d does not show a likewise continuous and large increase after the first 2 ns. Although the slight further increase signifies ongoing conformational changes, the near constancy of the curve between 4 ns and 10 ns seems to indicate that the peptide is approaching a new stable state. The 10-ns snapshot in Fig. 5 d shows that the initial circular shape is lost. Interestingly, the coils now exhibit several turns while retaining an overall structure, which remotely resembles a triangular β-helix. This finding has inspired us to speculate that triangular poly-Gln β-helices might be stable, and therefore we carried out simulations of such poly-Gln structures.

Fig. 6 a shows the 10-ns temporal evolution of the 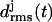values for the three coils of the triangular poly-Gln β-helix (cf. Methods). Surprisingly, all three 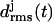curves behave just like those of the native LpxA fragment in Fig. 3 c. After 10 ns, the value of 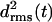belonging to the central coil 2 is <0.7 Å, whereas the partially water-exposed coils 1 and 3 exhibit higher values (1.5 Å and 2.0 Å, respectively). As a result, the three-coiled triangular poly-Gln β-helix is apparently as stable as the corresponding native LpxA fragment. In Fig. 6 b, the black and light shaded structures represent averages over the first 2.5 ns and the last 3 ns, respectively. Their good match visualizes the asserted structural stability. In particular, the central coil 2 is seen to be perfectly preserved.

FIGURE 6.

(a) 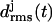curves for the various coils j of a three-coiled triangular poly-Gln β-helix. The gray scale (black, shaded, and light shaded) distinguishes three simulation periods. (b) Average structures of the three coils for the black and light shaded simulation periods.

To check this surprising result we have carried out additional 8-ns stability tests at an elevated temperature of 330 K both for the triangular three-coiled poly-Gln model and for the corresponding fragment of the native LpxA β-helix. The results of these tests are documented in the first figure of the Supplementary Material and demonstrate that the poly-Gln model becomes additionally stabilized by raising the temperature, which is a clear signature of hydrophobic stabilization. In contrast, the LpxA fragment appears to have lost some of its stability at these conditions.

In summary, three-coiled triangular poly-Gln β-helices are calculated to be at least as stable as fragments of a natively stable β-helix. Therefore, they should be sufficiently stable as to qualify as building blocks for amyloid fiber aggregation.

Our finding that the stability of β-helical fragments increases with the number of coils, which we derived from the comparison of two- and three-coiled LpxA fragments, now suggests that a two-coiled triangular poly-Gln β-helix might be unstable. As demonstrated by the second figure in the Supplementary Material, this is actually the case: The 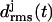curves and 4-ns snapshot are similar to those of the two-coiled LpxA fragment depicted in Fig. 3, a and b).

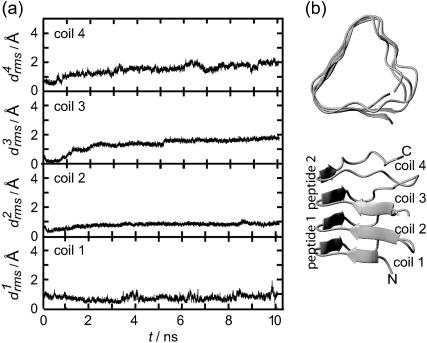
Now the important question arises as to whether the aggregation of two individually unstable two-coiled structures can stabilize the resulting dimer. To clarify this issue Fig. 7 a shows the 10-ns 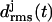curves for the four coils of the poly-Gln dimer. After 10 ns the average value 〈d_rms〉(t) is 1.4 Å, which is of the same order of magnitude as the corresponding results for the three-coiled LxpA (1.6 Å) and poly-Gln (1.4 Å) models. Accordingly, the dimer is classified as stable. The 10-ns average structures depicted in Fig. 7 b verify this conclusion. Even the fast (2 ns) increase of 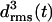to a value of 2 Å, exhibited in Fig. 7 a, does not change this result, because visual analysis of the structures reveals that the indicated change of coil 3 is confined to the N-terminus of peptide 2 and does not modify the overall shape of the aggregate. In summary, our data suggest that the dimerization of poly-Gln peptides, which comprise at least 36 residues, can create stable nuclei for seeded aggregation of triangular β-helices.

FIGURE 7.

(a) Coil-specific root mean-square deviations for a dimer of two-coiled triangular poly-Gln β-helices. (b) Average structure (10 ns, top and side views).

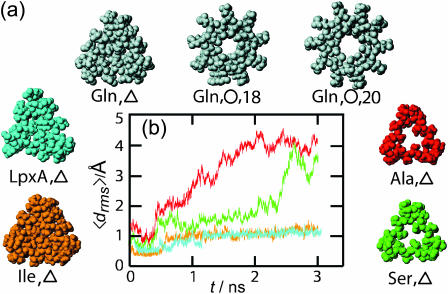
To find an explanation of why certain β-helices are stable and others preferentially decay, consider the space-filling models of three-coiled β-helices in Fig. 8 a. In the triangular LpxA, poly-Gln, and poly-Ile structures the centers of the helices are seen to be densely packed by the van der Waals spheres surrounding the atoms of the bulky nonpolar or weakly polar side groups. However, in some of the triangular structures (▵), that is, for the poly-Ala and poly-Ser models, and in the two circular poly-Gln structures (○) with 18 and 20 residues suggested by Perutz et al. (2002a), the peptide atoms leave sufficient space to open sizable channels near the centers of the β-helices. Upon hydration these channels become filled with 5–6 (Gln/○,18; Ala/▵; Ser/▵), and even 10 (Gln/○,20) water molecules per helical coil.

FIGURE 8.

(a) Space-filling models of various three-coiled β-helices viewed along their axes. (b) Average root mean-square deviations for the models colored in a from 3-ns simulations; color coding as in a.

The simulation results for some of these structures, presented above, now argue that β-helices are destabilized by water channels and are stabilized by hydrophobic interactions, if they have a sufficiently nonpolar and densely packed core. This argument implies that the triangular poly-Ser/▵ structure depicted in Fig. 8 a should decay, whereas poly-Ile/▵ should be stable.

Fig. 8 b compares the 〈d_rms〉(t) curves obtained by 3-ns simulations for poly-Ile/▵ (orange) and poly-Ser/▵ (green), with the reference curves of the stable LpxA (blue) and unstable poly-Ala (red) models, respectively. It shows that the predictions of the poly-Ser/▵ decay and of the poly-Ile/▵ stability are confirmed. Visual inspections of the final structures corroborate this result (data not shown). As a corollary we conclude that if poly-Gln β-helices exist, they are by no means water-filled nanotubes, in contrast to the expectation of Perutz et al. (2002a).

DISCUSSION, BIOMEDICAL IMPLICATIONS,AND A MODEL FOR PRP^SC

Originally, our MD-based stability study of parallelβ-helices had been designed to check the suggestion of Perutz et al. (2002a) that the poly-Gln amyloid fibers involved in Huntington's disease are composed of circularβ-helices. For the proposed 18 and 20 residues per coil, the circular structures turned out to be unstable. However, in the 20-residue case, after 10 ns of simulation, the structure remotely resembled a triangular β-helix.

This observation inspired us to examine left-handed triangular poly-Gln β-helices with 18 residues per coil as is common in native structures (Jenkins and Pickersgill, 2001). We found that a triangular three-coiled poly-Gln model is at least as stable as a native fragment of LpxA of the same size. A similar stability was determined for a dimeric aggregate of two-coiled poly-Gln β-helices, which, when considered individually, were found unstable.

Our results suggest that the dimerization of poly-Gln peptides with at least 36 residues can form stable nuclei for the aggregation of amyloid protofibrils shaped as triangular β-helices. However, in the case of poly-Gln peptides with ∼54 residues, a dimerization should not be required anymore. These conclusions agree well with the repeat length-dependence of disease risk (Ross et al., 2003) and of nucleation kinetics observed for poly-Gln peptides in vitro (Chen et al., 2001). Here, only Gln repeats with at least 37 residues were found to efficiently promote amyloid formation and Huntington's disease was attributed by Ross et al. (2003) to repeats exceeding 35–45 residues.

Our conclusions also agree with an in vitro mutational analysis of the structural organization of poly-Gln aggregates (Thakur and Wetzel, 2002). In this study the aggregation kinetics of various poly-Gln peptides with occasional Pro-Gly insertions has been investigated, because Pro-Gly inserts are known to be compatible with β-turn formation and incompatible with β-extended chain. Interestingly, the spontaneous aggregation kinetics of a K₂-(Q₁₀-PG)₃-Q₁₀-K₂ peptide was found to be as fast as that of a pure poly-Gln peptide (K₂-Q₄₅-K₂) (Thakur and Wetzel, 2002). The 12 residues of a (Q₁₀-PG) repeat exactly cover two thirds of a coil in a triangular left-handed parallel β-helix with the PG residues located at the second turn. Thus, this type of repeat unit is extremely compatible with the suggested secondary structure. Other repeat units, e.g., (Q₇-PG) or (Q₈-PG), in peptides of similar size were found to aggregate much less readily (Thakur and Wetzel, 2002) and are incompatible with the structure of a triangular parallel β-helix. A somewhat slower aggregation than for the pure poly-Gln peptide was found for (Q₉-PG) repeats (Thakur and Wetzel, 2002). When matching such sequences to a triangular parallel β-helix one would have to require that the corresponding helical coils contain short-cut turns rendering coils with <18 residues. Note here that such short-cut turns and coils with <18 residues also occur in native parallel β-helices (Jenkins and Pickersgill, 2001). Therefore, also, the result on the (Q₉-PG) aggregation is still compatible with the suggested secondary-structure motif. Thus, our results and the quoted in vitro data support the speculation that the core structure of the poly-Gln-induced amyloid fibers in Huntington's disease is that of a triangular β-helix with 18 residues per coil.

Based on our findings the question arises whether parallel β-helices may also feature in other diseases, such as prion diseases, that are linked to seeded aggregation and amyloid formation. Wille et al. (2002) suggested triangular β-helices as the decisive structural motif promoting PrP^Sc amyloid formation and provided a model by matching the hamster PrP sequence from about residue 90 to about residue 176 onto a regular triangular β-helix covering five layers arranged in a planar hexamer. However, all possible alignments of the hamster PrP sequence with this structure imply that some charged residues are located in the interior of the β-helix. In contrast, in native triangular β-helices charged residues exclusively point out of the helix or are found within loops, which generally protrude from the turns (Jenkins and Pickersgill, 2001). Moreover, no native hexamer of β-helices has been published, whereas several trimeric structures are known (Jenkins and Pickersgill, 2001).

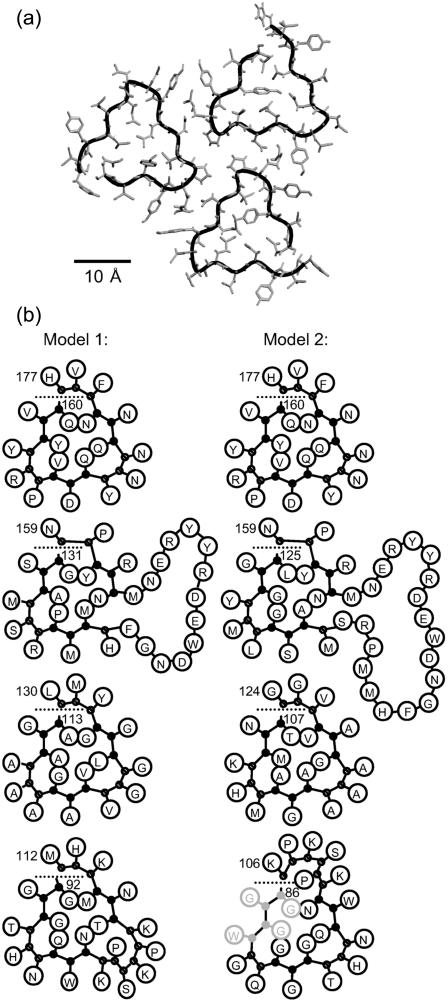
Because of these objections we considered a trimer model (see Fig. 9 a), which fits the size constraints imposed by electron microscopy analysis (Wille et al., 2002) and can easily accommodate loops. Based on alternative alignments of the sequence by allowing loops to protrude from the outside corners of identical four-layered beta-helices in a trimeric arrangement, we selected two refined models that both avoid charged residues in the interior of the β-helix and steric interference at the trimer interface, as depicted in Fig. 9 b. Because our above findings suggest that Gln side chains in the interior of a triangular β-helix can stabilize such a secondary structure, we here consider Gln side chains as an adequate filling material, although Gln does not occur inside the native left-handed trimeric β-helices listed in Jenkins and Pickersgill (2001). Correspondingly, both models exhibit several Gln side chains in the core of the β-helix. The models comprise, apart from their otherwise regular β-helical structure depicted in Fig. 1, e and f, one small loop (residues 101–105), one bigger loop (residues 140–153 in model 1, residues 134–153 in model 2), and one tight corner (residues 158, 159). In model 1 both loops protrude from the same corner, as is found in all natively trimeric β-helical proteins listed in Jenkins and Pickersgill (2001). In contrast, model 2 exhibits loops at different corners and, therefore, represents an unusual structure. Besides, both models present a Tyr-Tyr-Arg motif in an outward loop, which has been implied as a PrP^Sc-specific epitope (Paramithiotis et al., 2003).

FIGURE 9.

(a) Trimer model of PrP^Sc constructed from triangularβ-helices; shown are residues 160–177. (b) Two triangular β-helix models for PrP^Sc with four coils. Model 1 comprises residues 92–177, and model 2 residues 86–177; residues 86–89 may not be part of the helix anymore. The orientation of the single coils in the trimeric arrangement corresponds to the upper right coil in a.

Note that very recently, Govaerts et al. (2004) published an alternative refined version of the model of Wille et al. (2002), also using a trimeric instead of a hexameric arrangement, but with a sequence alignment differing from our suggestions. As in our model 2, in the model of Govaerts et al. (2004) the loops protrude from different corners, and in one case, a loop starts even within a side of the β-helix. As a result the β-helical coil at the top layer is neither complete nor regular. Such defects could hamper fiber growth which is supposed to proceed through aggregation of an unfolded soluble monomer to a structural template provided by a complete β-helical coil of the existing oligomer. Note furthermore that a different trimeric model using stackedβ-sheets, recently published by DeMarco and Daggett (2004), would fit into the electron microscopy images.

Testing models other than poly-Gln by MD simulations is hampered by the uncertainties of sequence alignment (including loop structures) and by the sheer sizes of the presumed aggregation nuclei. Whereas in the poly-Gln case these nuclei may actually be specifically folded monomers (Chen et al., 2002) larger complexes appear to be required with other polypeptides such as prion proteins (Eigen, 1996). Nevertheless, corresponding models may be valuable, because they entail predictions regarding the effect of amino acid exchanges on the stabilities of monomeric and oligomeric structures, which can be tested experimentally.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org