Abstract
The structure of cubic Cowpea mosaic virus crystals, compressed at 330 MPa in a diamond anvil cell, was refined at 2.8 Å from data collected using ultrashort-wavelength (0.331 Å) synchrotron radiation. With respect to the structure at atmospheric pressure, order is increased with lower Debye Waller factors and a larger number of ordered water molecules. Hydrogen-bond lengths are on average shorter and the cavity volume is strongly reduced. A tentative mechanistic explanation is given for the coexistence of disordered and ordered cubic crystals in crystallization drops and for the disorder-order transition observed in disordered crystals submitted to high pressure. Based on such explanation, it can be concluded that pressure would in general improve, albeit to a variable extent, the order in macromolecular crystals.
INTRODUCTION
Investigation of the dynamic nature of macromolecules from static structures often requires biophysical perturbation. The most widely used perturbation is temperature. However, temperature causes simultaneous changes in the volume and thermal energy of a system, which are difficult to separate. Pressure is another thermodynamic perturbation that offers many advantages in biophysical studies. It affects only the volume of a system and therefore the change in energy is better defined thermodynamically (Paci and Marchi, 1996). Its action is often reversible and can stabilize some structural intermediates. The compressibility of macromolecular structures reflects conformational fluctuations of proteins (Cooper, 1976; Gekko and Hasegawa, 1986). Pressure could be exploited as “thermodynamic tweezers” to investigate protein-protein interactions (Silva et al., 2001). Pressure is also an important environmental variable. Some deep-sea organisms live at pressures of over 100 MPa, and understanding how proteins from piezophilic organisms function optimally at extreme conditions requires accurate structural description.
Therefore, it is of great interest to study pressure-perturbed macromolecular structures. Traditionally, spectroscopic methods (Heremans and Smeller, 1998), including NMR (Jonas, 2002), were the methods of choice in high-pressure studies producing low-resolution data on the perturbed systems. The pressure-induced changes on the protein structures were first investigated to near atomic definition by using the variations of chemical shifts measured by NMR as the constraints in molecular dynamics calculations (Refaee et al., 2003). The method, however, is currently only applicable to relatively small macromolecules. X-ray crystallography at high pressure provides a unique opportunity to investigate in atomic detail the dynamic nature of larger macromolecules. Previously, diffraction studies of hen egg-white lysozyme (HEWL) at 100 MPa (Kundrot and Richards, 1987) and sperm whale myoglobin at 150 MPa (Urayama et al., 2002) were carried out using beryllium cells (Kundrot and Richards, 1986). Improvement of technology with diamond anvil cells (DAC) led to crystallographic studies of HEWL at 820 MPa and bovine Cu,Zn superoxide dismutase at beyond 1 GPa (Fourme et al., 2001). HEWL structure at 700 MPa was also determined and refined to 1.6 Å resolution (Fourme et al., 2002a).
The few macromolecular structures at high pressure determined up to now are of relatively small proteins only. Cowpea mosaic virus (CpMV) is a macromolecular assembly under extensive structural and molecular investigations (Lomonossoff and Johnson, 1991; Lin and Johnson, 2003). The complex structure provides an excellent model system for understanding the high-pressure effects on macromolecules. We found, through gradual ramping of the pressure and systematic diffraction studies, that pressure greatly enhanced the diffraction, probably by inducing a disorder-order transition on cubic CpMV crystals (Fourme et al., 2002b). Here we report the 2.8-Å resolution structure of such crystals at high pressure (HP) and the comparison with the 2.8-Å resolution structure at atmospheric pressure (AP).
EXPERIMENTAL PROCEDURES
Data collection at 330 MPa and 295 K
Data were collected on the high-pressure ID30 beamline at the ESRF. The wavelength was 0.3310 Å, close to the K absorption edge of barium, to maximize the detective quantum efficiency of the MAR345 imaging plate detector for elastic scattering while reducing the contribution from Compton scattering (Fourme et al., 2001). The crystal-to-detector distance was 1370 mm. Crystals with edges ∼170 μm were mounted in DAC and slowly compressed as described in Fourme et al. (2001, 2002). The standard stabilization solution (32% 2-methyl-2,4-pentanediol, 200 mM ammonium sulfate, 3% PEG 8000, and 50 mM potassium phosphate buffer at pH 7.0) was used as the compression medium. The actual pressure in the pressure chamber was determined using the fluorescence from a ruby chip (details in Fourme et al., 2001). Data of the I23 form were collected at 330 MPa on eight randomly oriented crystals. Each crystal was translated several times to irradiate fresh zones. Data were integrated using the program DENZO (Otwinowski and Minor, 1997). Integrated intensities were scaled and merged using SCALA (CCP4, 1994). A scaled and merged HP data set with completeness 91.2% at 2.8 Å resolution (I/σ(I) cutoff = 2) and Rmerge = 14.9% was obtained (detailed description of experimental procedures and data collection results in Fourme et al., 2003).
Refinements
High-pressure structure
The 330 MPa CpMV structure was refined on the basis of the HP data set using the program CNS (Brunger et al., 1998). The maximum-likelihood target function was utilized. The scripts were set up to automatically compute a cross-validated σA estimate. Data from the whole 50–2.8 Å resolution range were used without any σ-cutoff. Bulk solvent correction, as well as anisotropic B-factor correction, was used. Strict fivefold noncrystallographic symmetry was applied. The standard CNS libraries have been used without any modification.
The refined crystal structure (Protein Data Bank entry code 1NY7) determined at 2.8 Å resolution (Lin et al., 1999) was used as the starting model. An initial rigid-body refinement, using the L and S subunits as rigid bodies, followed by a step of slow cooling, led to R and Rfree (Brunger, 1992) residuals of 22.4% and 23.1%, respectively. The atomic model was inspected using the program O (Jones et al., 1991). Manual rebuilding of the model was alternating sequences of Powell minimization and individual B-factor refinement. Water molecules were included in the model both automatically and manually if they corresponded to peaks >3 σ deviation in the difference density map |Fo|-|Fc|. These molecules were retained if they formed stereochemically reasonable hydrogen bonds (distances to closest atoms in the range 2.6–3.4 Å) and if their electron densities in the 2|Fo|-|Fc| map were >1 σ.
Quality of the model was checked using CNS and PROCHECK (Laskowski et al., 1993).
Atmospheric pressure structure
The 1NY7 and HP structures were solved and refined using different programs and procedures. For structural comparison, a refinement of the atmospheric pressure structure was performed using CNS and following the strategy used for HP. This refinement was based on the structure factor amplitude file used to refine the 1NY7 model. The complete HP structure was used as a starting model. In effect, this structure can be used as a reference since it is better defined than the atmospheric pressure structure. On the one hand, the completeness in the last resolution shell is higher (88.6% against 36% for the HP and 1NY7 data sets, respectively) and, further, the overall thermal motion is lower and the number of ordered water molecules is larger in HP.
As was done for HP, an initial rigid-body refinement, with the L and S subunits, the water molecules, and the ions defined as rigid bodies, was followed by a step of slow cooling and individual B-factor refinement. At this stage, water molecules initially present in the HP were inspected one by one using O. They were kept in the model if they formed stereochemically reasonable hydrogen bonds according to the same criteria used for the HP model refinement, and if their densities in the |2Fo|-|Fc| map were >1 σ. Two such inspections were performed, and each inspection was followed by Powell minimization and individual B-factor refinement. At the end of this procedure the R and Rfree factors were 16.5% and 17.5%, respectively. The model (AP structure) consists in 4343 nonhydrogen protein atoms, 5 sulfate ions, and 1 caesium ion, as for the HP model, but only 99 water molecules were kept according to the criteria described above.
Overall asymmetric units, as well as domain displacements, were analyzed using the program LSQKAB (CCP4 suite, 1994). The root mean-square deviations on Cα positions between the two structures were calculated using the RMSD script in CNS with the best-fit option.
Capsid volume determination
As the capsid particle is centered on the crystal cell origin, the capsid radius in each structure was estimated as the average distance of all atoms to the origin. The volume of the sphere with this radius was considered as the capsid volume. This simplified procedure is sufficient, since only relative variations between the AP and the HP structures are of interest here.
Protein/domain volumes
Volumes were calculated with the program VOIDOO (Kleywegt and Jones, 1994). Calculations were performed on the whole icosahedral asymmetric unit (A, B5, and C domains) and on each domain separately. The following parameters were used in the calculations: initial grid spacing, 0.5 Å, and grid shrink factor, 0.95. Volumes were refined using successively finer grids until convergence (convergence criteria, 0.1 Å and 0.1%). Slightly different results were obtained when using different orientations of the model. Thus, the accuracy of volume calculations was estimated by repeating the calculations on nine randomly oriented copies of the model. A probe radius of 0.0 Å was used.
Cavity volume determination
Cavity volumes were calculated with VOIDOO (Kleywegt and Jones, 1994). Two calculations were performed, the first one on the icosahedral asymmetric unit (S and L domains), and the second one on the icosahedral asymmetric unit with neighboring molecules as shown in Fig. 1. The following parameters were used for the first calculation: initial grid spacing, 0.5 Å; van der Waals growth factor, 1.1; grid shrink factor, 0.95; and minimum size parameter for “real” cavity, 15 voxels. The same parameters were used for the second calculation, except that the initial grid spacing was set to 0.53 Å. Probe-accessible volumes were evaluated. In both calculations, cavity volumes were refined using successively finer grids until convergence (convergence criteria, 0.1 Å and 0.1%). The accuracy of volume calculations was also estimated by repeating the calculations with nine randomly oriented copies of the model. Different probe sizes were tried. Probe radii of 1.0 and 1.2 Å gave the most reliable results for the first and second calculations, respectively.
FIGURE 1.
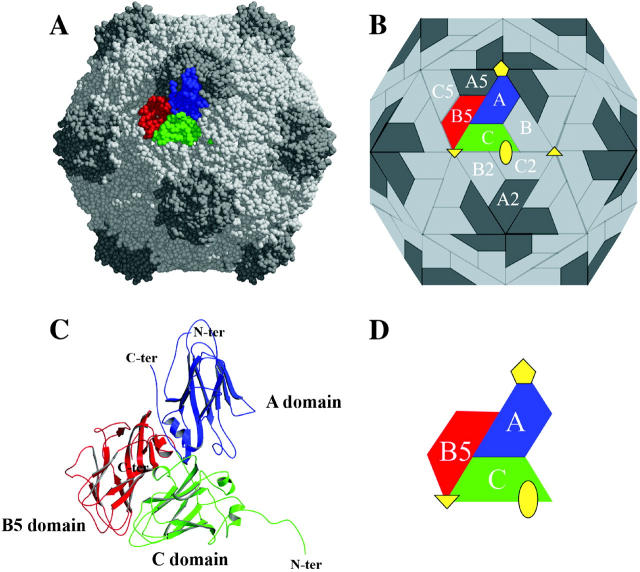
Organization of the CpMV capsid. (A) CPK representation of CpMV capsid. (B) Schematic representation of CpMV capsid showing the unique intersubunit interfaces (A/B5, C/B5, A/C, A/A5, A/B, B/C, C/B2 and C/C2). (C) Ribbon diagram of the three β-barrel domains that comprise the icosahedral asymmetric unit. (D) Schematic diagram of the icosahedral asymmetric unit with symmetry axes. The figure was prepared using MolScript (Kraulis, 1991).
Buried surface analysis
Buried surface areas were calculated with the MS program (Connolly, 1993), using a probe radius of 1.7 Å. Domain nomenclature refers to Fig. 1 according to Lin et al. (1999).
Hydrogen bond analysis
Hydrogen bond information was obtained using the program HBplus (McDonald and Thornton, 1994) with default parameters. For structure comparison, only values for common hydrogen bonds were kept for statistical calculations.
RESULTS
Pressure-improved diffraction of CpMV crystals
CpMV crystals were obtained as reported (Lin et al., 1999); ∼10% of these crystals conformed strictly to characteristics of the I23 space group (a = 317 Å), in which the structure was determined at 3.5 Å resolution (Stauffacher et al., 1987) and refined at 2.8 Å resolution (Lin et al., 1999). For the other crystals, weak reflections with h + k + l = 2n + 1 (odd reflections) are observed. These crystals have high mosaicity, diffract to low resolution, and were tentatively assigned to the P23 space group. Compressing P23 crystals beyond ∼240 MPa systematically removed odd reflections while dramatically improving both mosaicity and resolution (Fourme et al., 2002b). A highly complete 2.8-Å data set (summary in Table 1) was acquired at 330 MPa (Fourme et al., 2003). This set was used for the subsequent analysis of the HP structure.
TABLE 1.
Data processing of the HP set
| Wavelength (Å) | 0.3310 |
| Space group | I23 |
| Cell parameters (Å) | a = 313.38 |
| Resolution range (Å) (last shell) | 50– 2.8 (2.95–2.80) |
| No. of observed reflections | 389239 |
| No. of unique reflections | 113844 |
| Signal/noise ratio I/σ(I) | 4.9 (2.0) |
| Completeness (%) | 91.2 (88.6) |
| Multiplicity | 3.4 (3.1) |
| Rsym (%) | 14.9 (36.8) |
Detailed results can be found in Fourme et al. (2003).
Compression of unit cell and virus capsid
At 330 MPa, CpMV crystals have a unit cell parameter of 313.4 Å. The corresponding unit cell volume is 3.08 × 107 Å3. The value at atmospheric pressure is 317.0 Å (Lin et al., 1999). Thus, at 330 MPa, the unit cell volume was reduced by 3.4%. The average compressibility from atmospheric pressure to 330 MPa is 0.1 GPa−1, which is similar to the compressibility of tetragonal HEWL crystals in the range 0.1–800 MPa (Fourme et al., 2001). This analysis is based on the whole data set instead of a single oscillation picture (Fourme et al., 2002b), which improves the accuracy.
The variation of the capsid volume is roughly the same as the unit cell volume. The capsid volumes for the atmospheric pressure structure and the HP structure were 8.21 × 106 Å3 and 7.91 × 106 Å3 respectively. The capsid volume was thus reduced by 3.7% at 330 MPa.
Overall HP structure
The main structural features of CpMV were previously described by Lin et al. (1999). These features are maintained at high pressure, and a summary is provided here for comparison. Fig. 1 shows the structure of the capsid and the icosahedral unit. S (21 kDa) and L (41 kDa) proteins form three jelly-roll β-sandwich domains (A domain in S, B5 and C domains in L) in the icosahedral asymmetric unit. These domains occupy spatially equivalent positions to those found in T = 3 viruses formed by a single gene product. The jelly-roll β-sandwiches of the individual domains are topologically identical and structurally similar despite the complete lack of sequence homology. Accordingly, the CpMV capsid (3.72 MDa) is best described as a pseudo T = 3 (P = 3) particle with B and C domains clustered about the icosahedral threefold axes and five A domains clustered at the pentamer axes. The wedge-shaped β-sandwich structures are ∼50 Å long, 20 Å across at the narrow end, 30 Å at the wide end, and 20–30 Å in thickness. The C and B5 domains are connected by 10 residues that attach the terminus of the βC strand in the C domain with the β5 strand in the B5 domain. The connector lies internal at the RNA interface and links the C and B5 domains with nearly the minimum number of residues required to cover the distance between the two strand termini. The small subunit (A domain) deviates most from the canonical β-sandwich fold. The insert between βC and βD strands is extended and creates two additional strands on the top of the sandwich to make it a 10-stranded sandwich.
The final refined structure under high pressure includes the S (residues 1–189) and L (residues 1–369) subunits as well as 195 water molecules and six ions. The resulting R and Rfree factors (Brunger, 1992) are 16.3 and 17.1%, respectively. Residues 190–213 of S are susceptible to proteolysis in the purified virus and were apparently cleaved before crystallization (Kridl and Bruening, 1983; Lin et al., 1999).
More than 99% of nonglycine residues are located in the favored and allowed regions of the Ramachandran diagram (Ramachandran and Sasiskharan, 1968). The standard deviation on coordinates estimated from the Luzzati plot (Luzzati, 1952) is 0.24 Å. The root mean-square (rms) deviations from ideal values for bond lengths, bond angles, dihedral angles, and improper angles are 0.006 Å, 1.4°, 26.2°, and 0.8°, respectively.
Besides the original atoms in the CpMV structure at atmospheric pressure (Protein Data Bank entry, 1NY7; Lin et al. 1999), five additional sulfate ions were modeled. Three of these ions are located along the capsid fivefold axis in a channel connecting the exterior and the interior of the capsid. In the HP structure, C-terminus amino acids of both S (residues 185–189) and L (residues 366–369) are not visible in the 2|Fo|-|Fc| electron-density map contoured at 1 σ, whereas in the AP structure, the electron density of the C-terminus of the L domain was clearly visible at the same contour level. In HP, 195 water molecules were modeled, whereas only 99 water molecules were observed in AP.
Comparison of HP and AP structures
The rms deviation between atomic positions in HP and AP structures is 0.34 Å, whereas the rms deviation between 1NY7 and AP, which are based on the same set of structure factor amplitudes, but with a different refinement protocol, is 0.17 Å.
The displacements of the centroids of selected parts of AP and HP structures were calculated on the overall structure as well as for each domain. The displacements reflect essentially a radial movement toward the center of the capsid. Rotation matrices were also analyzed. The maximum rotation between AP and HP was <1°, indicating no particular rotation of the overall structure nor of any domain due to the high pressure.
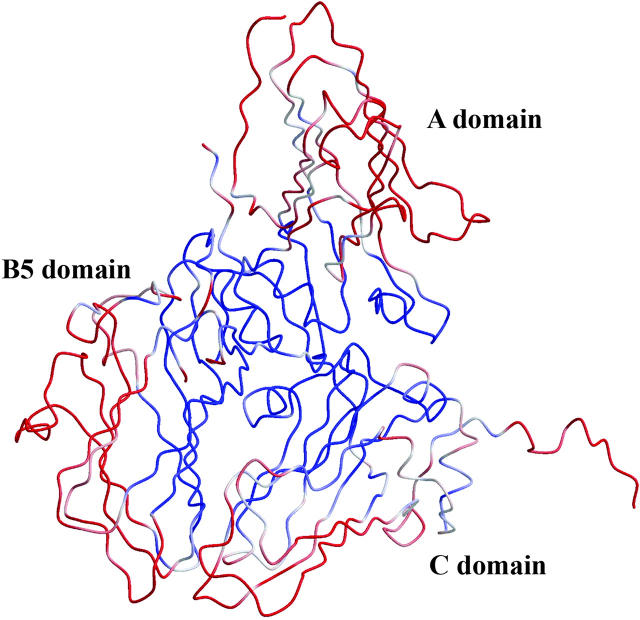
Fig. 2 shows the rms deviations on Cα atoms between the HP and AP structures. The smallest changes are found around the pseudo threefold axis while the subunit contacts between the asymmetric units are most pressure-sensitive. The rms deviations are greater for the A domain than for the two domains of the L subunit.
FIGURE 2.
Superimposition of the asymmetric unit of CpMV in the AP and HP structures. Structures were superimposed to minimize the rms interatomic distance difference on main-chain atoms (0.34 Å). The structure is colored according to the rmsd (rms deviation) value (rmsd < 0.33 Å in blue, 0.33 Å < rmsd < 0.35 Å in white, and rmsd > 0.35 Å). Figs. 2, 3, and 6 were prepared using BOBSCRIPT (Esnouf, 1999) and rendered using Raster3D (Merritt and Bacon, 1997).
Comparison of Debye-Waller factors
Table 2 summarizes the overall average individual temperature factors for each protein domain as well as for water molecules. The average temperature factors for HP are globally lower than those of AP by ∼8–9 Å2. No particular systematic trend can be drawn from the comparison of the temperature factors of corresponding domains in the HP and AP structures, nor for water molecules.
TABLE 2.
Mean B factors in the AP and HP structures
| Mean B factor (Å2) | HP structure | AP structure |
|---|---|---|
| S and L proteins | 20.30 | 29.17 |
| Main chain | 19.75 | 28.78 |
| Side chains | 20.84 | 29.54 |
| A domain | 24.01 | 32.56 |
| Main chain | 23.73 | 32.44 |
| Side chains | 24.21 | 32.61 |
| B5 domain | 19.63 | 28.05 |
| Main chain | 19.29 | 27.85 |
| Side chains | 19.98 | 28.20 |
| C domain | 17.08 | 26.77 |
| Main chain | 16.08 | 25.94 |
| Side chains | 18.16 | 27.68 |
| Water molecules | 24.84 | 30.26 |
Three zones of the protomer show increased temperature factors in the HP structure. The three zones correspond to the C-terminal residues (180–189) of the S domain and residues 219–225 and 365–369 from the C-terminal of the L domain.
Protein and domain volumes
Volumes of the protein for the whole icosahedral asymmetric unit (S and L proteins) as well as for each domain (A, B5, and C) were calculated. Volumes for HP are systematically smaller than those for AP, but the relative volume variations do not exceed 0.2%.
Buried surfaces
As shown on Fig. 1, the unique interfaces between subunits are A/B5, C/B5, A/C, A/A5, A/B, B/C, C/B2, and C/C2. The buried surface areas at each interface for both HP and AP are listed in Table 3. Differences in buried surfaces are small except for the A/B5 contact region, which is increased by more than 4%. Moreover, in HP, four additional residues are involved in the A/B5 contact.
TABLE 3.
Buried surfaces in the AP and HP structures, with number of residues involved in each interface
| HP
|
AP
|
|||||||
|---|---|---|---|---|---|---|---|---|
| Contact regions | No. of residues for subunit 1 | No. of residues for subunit 2 | Area (Å2) | No. of residues for subunit 1 | No. of residues for subunit 2 | Area (Å2) | Difference (Å2) | Difference (%) |
| A/B5 | 34 | 28 | 1672.3 | 32 | 26 | 1603.8 | 68.5 | 4.27 |
| C/B5 | 34 | 39 | 2219.6 | 34 | 39 | 2231.2 | −11.6 | −0.52 |
| A/C | 26 | 32 | 1706.7 | 28 | 32 | 1722.6 | −15.9 | −0.92 |
| A/A5 | 45 | 52 | 2805.5 | 52 | 45 | 2767.3 | 38.2 | 1.38 |
| A/B | 24 | 27 | 1393.2 | 24 | 28 | 1389.3 | 3.9 | 0.28 |
| B/C | 34 | 27 | 1801.6 | 34 | 27 | 1773.1 | 28.5 | 1.61 |
| C/B2 | 32 | 36 | 1987.3 | 32 | 37 | 1958.9 | 28.4 | 1.45 |
| C/C2 | 44 | 43 | 2389.4 | 42 | 42 | 2352.0 | 37.4 | 1.59 |
Internal cavities
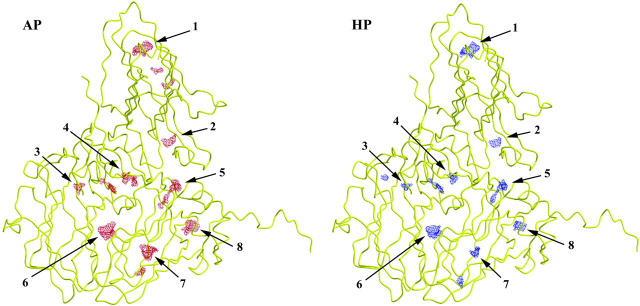
Table 4 and Fig. 3 display the changes of internal cavities under high pressure. Cavity volumes were calculated for the icosahedral asymmetric unit alone as well for all the subunits involved in unique interfaces considered as a whole, i.e., the icosahedral asymmetric unit and the A5, B, B2, and C2 domains (Fig. 1). In both calculations, there are fewer cavities with significantly smaller total mean volume at 330 MPa. If the icosahedral unit is considered alone, the total cavity volume is decreased by >40% (12%/100 MPa) in the HP model. The decrease remains large, 25%, when the domains involved in unique domain interfaces are also taken into account. Fig. 3 shows cavities for the reoriented copy of the model that leads to cavity volumes closest to the average cavity volumes calculated from copies with different orientations (see Experimental Procedures section). As can be seen in this figure, the volumes of all cavities identified in the AP model are reduced in the HP model. For the particular orientation of the model, some cavities have disappeared in the A domain of the HP structure whereas a small cavity in the B domain is only observed in the HP model (note that identification of small cavities by the program VOIDOO (Kleywegt and Jones, 1994) depends on the orientation of the model).
TABLE 4.
Data on cavities in the AP and HP structures calculated with VOIDOO
| Icosahedral unit
|
Icosahedral unit with neighboring molecules
|
|||||
|---|---|---|---|---|---|---|
| Mean cavity volume (Å3) | Standard deviation (Å3) | Mean number of detected cavities | Mean cavity volume (Å3) | Standard deviation (Å3) | Mean number of detected cavities | |
| HP structure | 65.9 | 2.6 | 10.8 | 168.0 | 22.8 | 16.2 |
| AP structure | 113.4 | 11.7 | 12.6 | 231.9 | 17.7 | 22.9 |
The mean volume and mean number of detected cavities are the rms values resulting from 10 random orientations.
FIGURE 3.
Pressure-induced changes in CpMV cavities. This figure shows the reoriented copy that gives cavity volumes closest to the average values obtained with different orientations of the model (see Experimental Procedures). Numbers make reference to Fig. 4.
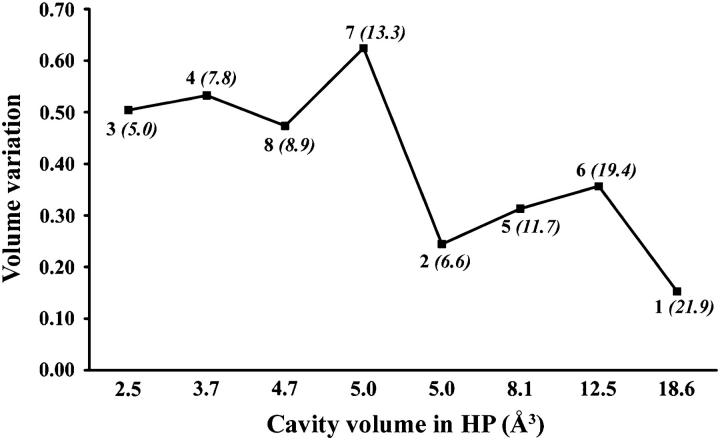
Fig. 4 shows the volume variation of the cavities detected in the icosahedral asymmetric unit with a probe radius of 1.0 Å as a function of their final volume. Two groups of cavities can be distinguished. In the first group, large volume variations, >40%, are observed whereas in the second group volume variations are smaller. No direct relationship with the presence of water molecules in the cavity, rms deviations, or B factors differences, can explain these two different behaviors. Generally, the larger cavities are less compressible than the smaller ones, but this is not the case for cavities 2 and 7. The vicinity of each cavity was analyzed considering the nature of the residues bordering the cavity. Cavities showing volume variations <40% comprise at least one charged residue delimiting the cavity as detected by the program VOIDOO (Kleywegt and Jones, 1994).
FIGURE 4.
Variation of the cavity volume between AP and HP as a function of the mean volume in HP. Numbers on the curve represent the cavity number (see Fig. 3) and the mean volume of the cavity in AP (in italic between brackets).
Hydrogen bonds
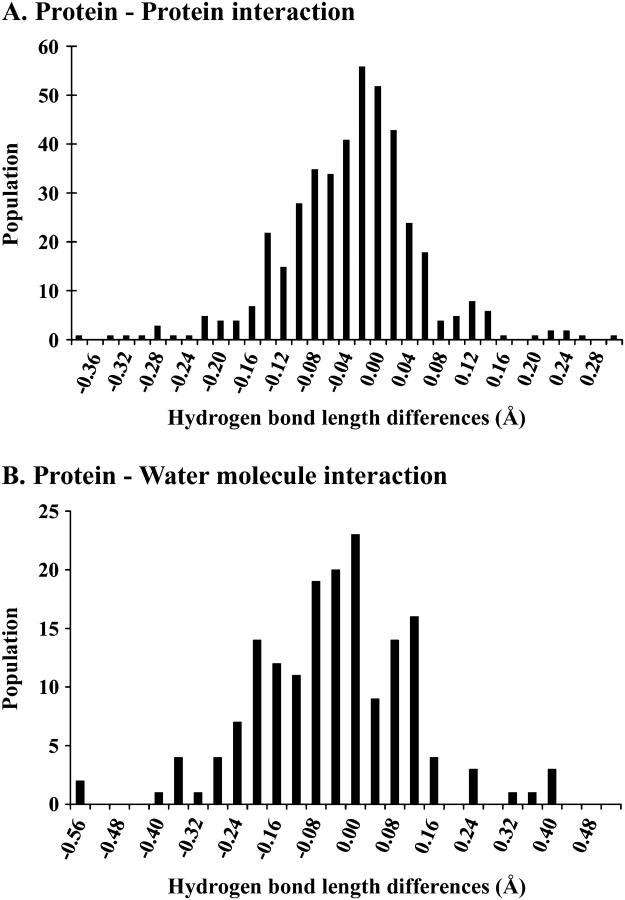
Table 5 summarizes changes of hydrogen bond lengths between the HP and AP structures. Only values of hydrogen bonds common to both structures were included in the statistics. Consequently, 428 measurements were obtained for hydrogen bonds occurring in the proteins through interactions between residues, and 169 measurements for hydrogen bonds between a residue and a water molecule. The overall statistical trend corresponds to a significant shortening of hydrogen bonds in the HP structure, whatever the considered protein domain. Fig. 5 shows the histograms of the differences in hydrogen bond lengths for both types of bonds. The overall population of the negative-difference classes is greater than for the positive-difference classes. This indicates that both distributions are shifted toward negative differences, which corresponds to an overall reduction in hydrogen bond lengths at high pressure. For hydrogen bonds between residues, differences are in the range −0.36 to 0.32 Å, with a mean value of −0.034 Å. For hydrogen bonds between a residue and a water molecule, the difference range is −0.57 Å to 0.41 Å, with a mean value of −0.048 Å.
TABLE 5.
Hydrogen bond lengths
| HP structure
|
AP structure
|
Difference HP-AP
|
|||||
|---|---|---|---|---|---|---|---|
| Hydrogen bond nature | No. of measurements | Mean value (Å) | Standard deviation | Mean value (Å) | Standard deviation | Mean value (Å) | Standard deviation |
| Protein-protein | 428 | 2.92 | 0.19 | 2.95 | 0.19 | −0.034 | 0.088 |
| Protein-water molecule | 169 | 2.87 | 0.21 | 2.92 | 0.22 | −0.048 | 0.158 |
| Water-water molecules | 24 | 2.84 | 0.17 | 2.94 | 0.25 | not calculated | not calculated |
FIGURE 5.
Histogram of hydrogen bond-length differences for (A) hydrogen bonds between residues and for (B) hydrogen bonds between protein atoms and water molecules.
The difference is greater, with a mean value of −0.1 Å, for hydrogen bonds between solvent molecules, but this result is of limited significance, since it is based on a small number (24) of common measurements between HP and AP structures.
Crystal packing
The crystal packing was analyzed and results can shed some light on the mechanism of the disorder-order transition observed in CpMV cubic crystals, as discussed later. In the unit cell, virus particles are packed with one capsid centered at (0, 0, 0) and the second centered at (1/2, 1/2, 1/2) (Fig. 6 A). In the I23 space group, icosahedral twofold and threefold axes coincide with crystallographic axes. The intercapsid contacts are along the threefold symmetry axes. Three zones of contact are involved.
FIGURE 6.
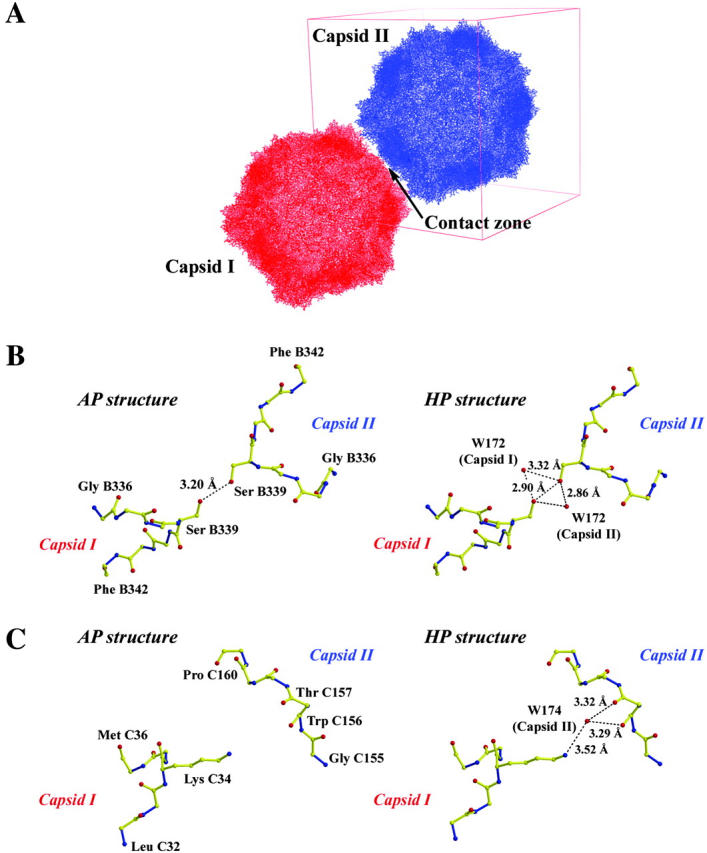
Changes in crystal packing due to high pressure. (A) Overall capsid packing. (B) B5-domain interaction zone. (C) C-domain interaction zone. (Fig. 6 A was prepared using PyMOL (DeLano, 2002).)
In the first zone, an alanine residue (C35) of the C domain faces an equivalent symmetry-related residue and the distance between their Cβ (2.82 Å and 2.85 Å, in AP and HP, respectively) remains nearly unchanged under high pressure.
The second zone of contact involves residues of the B5 domain. As shown in Fig. 6 B, the hydrogen bond between serine B339 and an equivalent symmetry-related serine is reduced by 0.3 Å at high pressure. Moreover, in the HP structure the hydrogen bond network is reinforced by the presence of a water molecule, W172, and the symmetry-related water molecule.
Due to threefold symmetry, the first two contact zones appear three times at the contact surface.
The third zone of contact is only present in the HP structure and involves residues of the C domain. A hydrogen network is created by the presence of a water molecule. As shown in Fig. 6 C, this network is made of the Nζ atom of lysine C34, the water molecule W174, and the main chain C=O groups of tryptophan C156 and threonine C157, as shown in Fig. 6 C. This contact zone appears six times at the intercapsid zone of contact.
The refinement was performed in parallel on the two structures with data of similar quality and resolution, using the same programs, procedures, and cutoff values and applying NCS averaging. Accordingly, we think that differences in water structure and interactions are significant.
Disorder-order transition
As previously mentioned, only ∼10% of CpMV crystals grown at atmospheric pressure conform strictly to the I23 space group (i.e., no reflections with indices of h + k + l = odd). For other crystals, weak reflections with indices of h + k + l = odd are visible. They exhibit large mosaicity and modest resolution, which indicates some kind of disorder. The unit cell is still cubic and the cell parameter is unchanged within the accuracy of measurements. Space group P23 was tentatively assigned to these crystals. The starting point of the structural study of the CpMV under high pressure was the observation that pressure induces systematically a transition from P23 to I23 crystals, leading to a dramatic improvement of resolution (Fourme et al., 2002a). From experiments at the European Synchrotron Radiation Facility (ESRF) made on different CpMV crystals, the transition occurs in a range of 230 ± 15 MPa (unpublished results). From several facts (e.g., coexistence of P23 and I23 crystals in the same crystallization drop with similar cell parameters and transition at high pressure without destruction of crystals), it is likely that the P23 structure is closely related to the I23 structure, which then can be taken as the basic structure. Along this line, it can be assumed that the disorder in the P23 structure is due to rotations of quasispherical capsids about their (invariant) center of gravity. A simplified mechanistic model for the disorder in the P23 form has been proposed, with the particle at the origin of the cell rotated by 1.5–3° relative to the body-centered particle (Lin et al., 2005). A more realistic model should include a statistical disorder.
This scheme is compatible with the 3D structures of the I23 form at atmospheric pressure and high pressure. In AP, the packing of capsids mainly involves one hydrogen bond between two symmetry-related serine residues (Fig. 6 B), which appears three times by symmetry. Based on the bond length (3.2 Å), this hydrogen bond is rather weak. In the HP form, packing interactions are stronger, because 1), the length of the hydrogen bond between serine residues is shorter; 2), a second hydrogen bond takes place (Fig. 6 C); and 3), additional water molecules extend the hydrogen bond network between adjacent particles (Fig. 6, B and C).
DISCUSSION
We have demonstrated the feasibility of data collection for solving and refining the structure of a complex macromolecular assembly under high pressure. Despite a rather high overall Rmerge (14.9%) due to relatively weak Bragg intensities, a complete data set to 2.8 Å resolution (signal/noise cutoff I/σ(I) = 2) was obtained (Fourme et al., 2003), which was the basis for a straightforward refinement of the structure with good R and Rfree values. This success relies heavily on the technical conditions used for high-pressure data collection (Fourme et al., 2003), in particular a large area detector located at a large distance from the sample, the use of quasiplane wave of ultrashort wavelength for highly efficient data collection and a high-brilliance x-ray source. The cubic unit cell and the CpMV crystals with roughly equal dimensions in all sides were particularly suitable for high-pressure data collection and allowed us to collect a highly complete data set with a relatively small number of crystals, despite the limited opening (42°) of the first-generation DAC and data collection at room temperature. The limited opening of DAC posed a serious limitation on data collection for crystals with symmetry lower than cubic or tetragonal. The problem would be compounded with anisotropic crystals (e.g., platelet) with restricted orientations to the diamond culets. With the increase in the opening of DAC (currently 62°, with planned modifications to reach 90°) and special procedures for sample loading (publication in preparation), these limits are being alleviated. These technical advances will have a direct impact on the maturation and the extension of applications of high-pressure macromolecular crystallography.
The average compressibility of the CpMV crystals from atmospheric pressure to 330 MPa is similar to the compressibility of tetragonal HEWL crystals in the range 0.1–800 MPa (Fourme et al., 2001). In both cases, to explain this fact, it can be concluded that the major contribution for compression arises from the solvent phase in crystals. The relative variation of the capsid volume at high pressure was measured (−3.7%). The root mean-square difference in atomic coordinates between the AP and HP structures is 0.34 Å. The overall organization of the capsid structure and the structures of S and L subunits of the asymmetric unit are only slightly modified at high pressure. The rms difference between the AP and 1NY7 structures (which result from two different refinements based on the same data set) is 0.17 Å. Although small, pressure-induced changes are significant and they are not evenly distributed. In particular, the core of the protomer near the pseudo threefold axis is only slightly affected whereas larger changes occur at the periphery (Fig. 2). For each jelly-roll β-sandwich domain, the volumes are systematically smaller at high pressure but the relative volume variations are small (<0.2%). Indeed, low compressibility of β-structure has been reported for the β-domain of HEWL both by NMR in solution at 200 MPa (Refaee et al., 2003) and by crystallography at 100 MPa (Kundrot and Richards, 1987).
For the A/B5 contact region, the interface area is increased by >4%. Domain A, which protrudes from the capsid surface, is also the region where atomic displacements produced by pressure are larger.
Pressure induces an overall translation movement of the icosahedral unit of ∼1.4 Å toward the center of the capsid. This radial movement is in agreement with the observed compression of the capsid.
High-pressure simulations (Marchi and Akasaka, 2001; Paci, 2002) showed increased interactions of proteins with water, whereas the number of hydrogen bonds within the protein itself is only slightly affected. The comparison between the AP and HP structures shows an identical number of hydrogen bonds detected within the protein domains. On the other hand, the number of ordered water molecules is nearly doubled at high pressure, and thus, an increased number of hydrogen bonds between water and protein is observed with increased pressure. Pressure-induced variations in hydrogen bond length have been obtained for a large number of measurements (428 residue-residue and 169 residue-water interactions, respectively). Hydrogen bonds are on average shorter at high pressure even if the average distance between acceptor and donor remains close to 2.8–2.9 Å. Such shortening is in agreement with the values observed at high pressure by NMR for the melittin α-helix (Iwadate et al., 2001), for BPTI (Li et al., 1998), or for lysozyme (Refaee et al., 2003).
The doubled number of observed water molecules combined with the reduction of hydrogen bond lengths indicate that, in the pressure range used in this experiment, the pressure tends to increase and stabilize the water molecule network, thereby increasing the stability of the protein-hydration shell system.
The overall thermal factor is reduced at high pressure by 9 Å2. This observation can be correlated to the intuitive argument that pressure tends to reduce the atomic mobility, in an analogous way to that produced by low temperature. Brunne and van Gunsteren (1993) have observed by simulations the decrease of positional fluctuations of atoms with increasing pressure. Moreover, a decrease in atomic mobility with pressure can be correlated with the increased number of ordered water molecules in the HP structure.
A major effect of high pressure on the CpMV capsid is to decrease the volume of the internal cavities. When only the icosahedral asymmetric unit is considered, this decrease is >40% for an applied pressure of 330 MPa. The behavior of the cavities depends mainly on the initial volume of the cavity. The smaller the cavity at ambient pressure, the greater the volume decreases at high pressure. No direct link could be drawn between this observation and domain movements or B-factor changes. Moreover, we have not observed an increase in the number of ordered water molecules inside the cavities. These observations could be related to protein unfolding by pressure. It has been observed that unfolding is generally preceded by a significant decrease in volume of the protein-solvent system. Two models have been proposed to explain protein unfolding by pressure (Hummer et al., 1998; Balny et al., 2002; Royer, 2002). In the most common model, the penetration of water into the protein structure leads to hydration of the protein inside, resulting in unfolding. In such processes, cavities may play an important role (Frye and Royer, 1998). From our study, it is clear that, in the pressure range below 400 MPa, the major pressure-induced effects on the CpMV arise from the change of internal cavities and from protein-water interactions through the increase of observed water molecules and the reduction in hydrogen bond lengths. The CpMV structure under high pressure gives a new experimental contribution for understanding the behavior of macromolecular systems.
The ensemble of results obtained on cubic CpMV crystals gives new insights on the structural transition. At atmospheric pressure, our hypothesis is that minute perturbations in the crystallization drop can produce small rotations of loosely connected capsids, thus destroying the perfect periodic arrangement of the I23 form in most crystals. Pressure ramping gradually increases the compactness of packing, thus reducing intercapsid distances and favoring ordering of water molecules. At ∼230 MPa, strengthening of intercapsid interactions would restore perfect long-range order in P23 crystals by forcing capsids to reorient to reference positions of the I23 form.
The development of high-pressure macromolecular crystallography will allow new experimental observations on pressure effects on biological systems. As pressure is a way to modify the Gibbs free energy, pressure allows the exploration of phase transitions and protein substates (Urayama et al., 2002). More globally, high-pressure macromolecular crystallography would provide detailed analysis of interactions between protein molecules within crystals, between monomers of an oligomeric protein, between components of a complex macromolecular assembly, and for water-water or water-molecule interactions. High-pressure macromolecular crystallography can probably be used to capture the first steps of protein denaturation induced locally by pressure. A better understanding of macromolecules under pressure will help us to understand the adaptation processes of piezophilic organisms, such as those from the deep sea or underneath the earth's surface. From the high-pressure study of CpMV, we have already demonstrated and achieved the detailed analysis of a complex macromolecular system. In particular, we have shown that pressure is a useful tool to investigate the role of solvent molecules and internal cavities in studies of protein structure and functions. Finally, in the particular case of CpMV, pressure has a dramatic effect on crystal order because it controls the degree of freedom of particles in the lattice. Such large effects may be limited to particular cases, such as nearly spherical particles. But the effect of pressure on strengthening intra- and interparticle interactions should be a general trend. Accordingly, pressure would in general improve the order in macromolecular structures, albeit to a variable extent, a conclusion which we think is of importance for the protein crystallography community.
Acknowledgments
We are grateful to the European Synchrotron Radiation Facility personnel and in particular staff members of beamline ID30 for excellent working conditions, from beam supply to beamline operation.
References
- Balny, C., P. Masson, and K. Heremans. 2002. High pressure effects on biological macromolecules: from structural changes to alteration of cellular processes. Biochim. Biophys. Acta. 1595:3–10. [DOI] [PubMed] [Google Scholar]
- Brunger, A. T. 1992. Free R value: a novel statistical quantity for assessing the accuracy of crystal structures. Nature. 355:472–474. [DOI] [PubMed] [Google Scholar]
- Brunger, A. T., P. D. Adams, G. M. Clore, P. Gros, R. W. Grosse-Kunstleve, J.-S. Jiang, J. Kuszewski, M. Nilges, N. S. Pannu, R. J. Read, L. M. Rice, T. Simonson, and G. L. Warren. 1998. Crystallography and NMR system CNS: A new software system for macromolecular structure determination. Acta Crystallogr. D. 54:905–921. [DOI] [PubMed] [Google Scholar]
- Brunne, R. M., and W. F. van Gunsteren. 1993. Dynamical properties of bovine pancreatic trypsin inhibitor from a molecular dynamics simulation at 5000 atm. FEBS Lett. 323:215–217. [DOI] [PubMed] [Google Scholar]
- CCCP4 (Collaborative Computational Program, No. 4). 1994. The CCP4 suite: programs for protein crystallography. Acta Crystallogr. D. 50:760–763. [DOI] [PubMed] [Google Scholar]
- Connolly, M. L. 1993. The molecular surface package. J. Mol. Graph. 11:139–141. [DOI] [PubMed] [Google Scholar]
- Cooper, A. 1976. Thermodynamic fluctuations in protein molecules. Proc. Natl. Acad. Sci. USA. 73:2740–2741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeLano, W. L. 2002. The PyMOL molecular graphics system. DeLano Scientific, San Carlos, CA, USA. http://www.pymol.org.
- Esnouf, R. M. 1999. Further additions to MolScript version 1.4, including reading and contouring of electron-density maps. Acta Crystallogr. D. 55:938–940. [DOI] [PubMed] [Google Scholar]
- Fourme, R., I. Ascone, R. Kahn, E. Girard, M. Mezouar, T. Lin, and J. E. Johnson. 2002a. New trends in macromolecular crystallography at high hydrostatic pressure. In Advances in High Pressure Bioscience and Biotechnology II. R. Winter, editor. Springer-Verlag, Berlin. 161–170.
- Fourme, R., I. Ascone, R. Kahn, M. Mezouar, P. Bouvier, E. Girard, T. Lin, and J. E. Johnson. 2002b. Opening the high-pressure domain beyond 2 kbar to protein and virus crystallography. Structure. 10:1409–1414. [DOI] [PubMed] [Google Scholar]
- Fourme, R., E. Girard, R. Kahn, I. Ascone, M. Mezouar, A.-C. Dhaussy, T. Lin, and J. E. Johnson. 2003. Using a quasi-parallel X-ray beam of ultrashort wavelength for high-pressure virus crystallography: implications for standard macromolecular crystallography. Acta Crystallogr. D. 59:1767–1772. [DOI] [PubMed] [Google Scholar]
- Fourme, R., R. Kahn, M. Mezouar, E. Girard, C. Hoerentrup, T. Prangé, and I. Ascone. 2001. High pressure protein crystallography HPPX: instrumentation, methodology and results on lysozyme crystals. J. Synchrotron Rad. 8:1149–1156. [DOI] [PubMed] [Google Scholar]
- Frye, K. J., and C. A. Royer. 1998. Probing the contribution of internal cavities to the volume change of protein unfolding under pressure. Protein Sci. 7:2217–2222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gekko, K., and Y. Hasegawa. 1986. Compressibility-structure relationship of globular proteins. Biochemistry. 25:6563–6571. [DOI] [PubMed] [Google Scholar]
- Heremans, K., and L. Smeller. 1998. Protein structure and dynamics at high pressure. Biochim. Biophys. Acta. 1386:353–370. [DOI] [PubMed] [Google Scholar]
- Hummer, G., S. Garde, A. E. Garcia, M. E. Paulaitis, and L. R. Pratt. 1998. The pressure dependence of hydrophobic interactions is consistent with the observed pressure denaturation of proteins. Proc. Natl. Acad. Sci. USA. 95:1552–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwadate, M., T. Asakura, P. V. Dubovskii, H. Yamada, K. Akasaka, and M. P. Williamson. 2001. Pressure-dependent changes in the structure of the melittin α-helix determined by NMR. J. Biomol. NMR. 19:115–124. [DOI] [PubMed] [Google Scholar]
- Jonas, J. 2002. High-resolution nuclear magnetic resonance studies of proteins. Biochim. Biophys. Acta. 1595:145–159. [DOI] [PubMed] [Google Scholar]
- Jones, T. A., J.-Y. Zou, S. W. Cowan, and M. Kjeldgaard. 1991. Improved methods for building protein models in electron density maps and the location of errors in these models. Acta Crystallogr. A. 47:110–119. [DOI] [PubMed] [Google Scholar]
- Kleywegt, G. J., and T. A. Jones. 1994. Detection, delineation and display of cavities in macromolecular structures. Acta Crystallogr. D. 50:178–185. [DOI] [PubMed] [Google Scholar]
- Kraulis, P. J. 1991. MolScript: a program to produce both detailed and schematic plots of protein structures. J. Appl. Crystallogr. 24:946–950. [Google Scholar]
- Kridl, J. C., and G. Bruening. 1983. Comparison of capsids and nucleocapsids from Cowpea mosaic virus-infected cowpea protoplasts and seedlings. Virology. 129:369–380. [DOI] [PubMed] [Google Scholar]
- Kundrot, C. E., and F. M. Richards. 1986. Collection and processing of X-ray diffraction data from protein crystals at high pressure. J. Appl. Crystallogr. 19:208–213. [Google Scholar]
- Kundrot, C. E., and F. M. Richards. 1987. Crystal structure of hen egg-white lysozyme at a hydrostatic pressure of 1000 atmospheres. J. Mol. Biol. 193:157–170. [DOI] [PubMed] [Google Scholar]
- Laskowski, R. W., M. W. MacArthur, D. S. Moss, and J. M. Thornton. 1993. PROCHECK: a program to check the stereochemical quality of protein structures. J. Appl. Crystallogr. 26:345–364. [Google Scholar]
- Li, H., H. Yamada, and K. Akasaka. 1998. Effect of pressure on individual hydrogen bonds in proteins. Basic pancreatic trypsin inhibitor. Biochemistry. 37:1167–1173. [DOI] [PubMed] [Google Scholar]
- Lin, T., Z. Chen, R. Usha, M. Harrington, T. Schmidt, and J. E. Johnson. 1999. The refined crystal structure of Cowpea mosaic virus at 2.8 Å resolution. Virology. 265:20–34. [DOI] [PubMed] [Google Scholar]
- Lin, T., and J. E. Johnson. 2003. Structures of Picorna-like plant viruses: implications and applications. Adv. Virus Res. 62:167–239. [DOI] [PubMed] [Google Scholar]
- Lin, T., W. Schildkamp, K. Brister, P. C. Doerschuk, M. Somayazulu, H. K. Mao, and J. E. Johnson. 2005. The mechanism of high pressure induced ordering in a macromolecular crystal. Acta Crystallogr. D. In press. [DOI] [PubMed]
- Lomonossoff, G. P., and J. E. Johnson. 1991. The synthesis and structure of comovirus capsids. Prog. Biophys. Mol. Biol. 552:107–137. [DOI] [PubMed] [Google Scholar]
- Luzzati, V. 1952. Traitement statistique des erreurs dans la détermination des structures cristallines. Acta Crystallogr. 5:802–810. [Google Scholar]
- Marchi, M., and K. Akasaka. 2001. Simulation of hydrated BPTI at high pressure: Changes in hydrogen bonding and its relation with NMR experiments. J. Phys. Chem. B. 105:711–714. [Google Scholar]
- McDonald, I. K., and J. M. Thornton. 1994. Satisfying hydrogen bonding potential in proteins. J. Mol. Biol. 238:777–793. [DOI] [PubMed] [Google Scholar]
- Merritt, E. A., and D. J. Bacon. 1997. Raster3D: photorealistic molecular graphics. Methods Enzymol. 277:505–524. [DOI] [PubMed] [Google Scholar]
- Otwinowski, Z., and W. Minor. 1997. Processing of oscillation data collected in oscillation mode. Methods Enzymol. 276:307–326. [DOI] [PubMed] [Google Scholar]
- Paci, E. 2002. High pressure simulations of biomolecules. Biochim. Biophys. Acta. 1595:185–200. [DOI] [PubMed] [Google Scholar]
- Paci, E., and M. Marchi. 1996. Intrinsic compressibility and volume compression in solvated proteins by molecular dynamics simulation at high pressure. Proc. Natl. Acad. Sci. USA. 93:11609–11614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandran, G. N., and V. Sasiskharan. 1968. Conformation of polypeptides and proteins. Adv. Protein Chem. 23:283–437. [DOI] [PubMed] [Google Scholar]
- Refaee, M., T. Tezuka, K. Akasaka, and M. P. Williamson. 2003. Pressure-dependent changes in the solution structure of hen egg-white lysozyme. J. Mol. Biol. 327:857–865. [DOI] [PubMed] [Google Scholar]
- Royer, C. A. 2002. Revisiting volume changes in pressure-induced protein unfolding. Biochim. Biophys. Acta. 1595:201–209. [DOI] [PubMed] [Google Scholar]
- Silva, J. L., D. Foguel, and C. A. Royer. 2001. Pressure provides new insights into protein folding, dynamics and structure. Trends Biochem. Sci. 26:612–618. [DOI] [PubMed] [Google Scholar]
- Stauffacher, C. V., R. Usha, M. Harrington, T. Schmidt, M. Hosur, and J. E. Johnson. 1987. The structure of Cowpea mosaic virus at 3.5A resolution. In Crystallography in Molecular Biology. D. Moras, J. Drenth, B. Strandberg, D. Suck, and K. Wilson, editors. Plenum Press, New York. 293–308.
- Urayama, P., G. N. Phillips, and S. M. Gruner. 2002. Probing substates in sperm whale myoglobin using high-pressure crystallography. Structure. 10:51–60. [DOI] [PubMed] [Google Scholar]