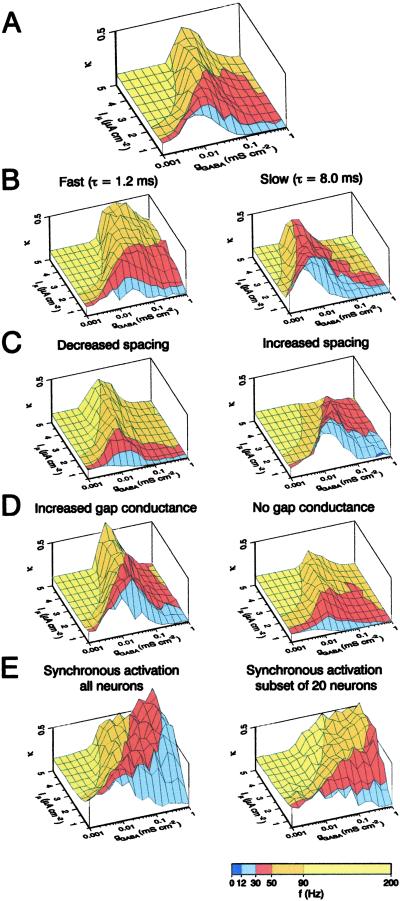
Figure 4.

Parameters that determine coherence and frequency in the interneuron network model. All graphs show coherence (κ) plotted against the amplitude of the unitary postsynaptic peak conductance (g_GABA) and excitatory drive (I_μ). Action potential frequency in the network is shown by superimposed color code (see scale bar at bottom). (A) Simulations with standard settings. Chemical and electrical synapses; biexponential synaptic conductance with decay time constants of 1.2 ms (90% amplitude contribution) and 8 ms (10%); 50 μm spacing; gap junction conductance 0.01 mS⋅cm⁻². (B) Influence of the decay kinetics of the inhibitory postsynaptic conductance. (Left) Fast monoexponential decay (decay time constant 1.2 ms). (Right) Slow monoexponential decay (decay time constant 8 ms). (C) Effects of spacing of neurons. (Left) Decrease in cell-cell distance by a factor of 2 (25 μm). (Right) Increase by a factor of 1.5 (75 μm). (D) Impact of electrical synapses. (Left) Increased gap junction conductance (0.02 mS⋅cm⁻²). (Right) Block of gap junctions. In all simulations (A–D) step-like driving currents were applied to individual neurons with randomized onset times of −150 ms ≤ t < −100 ms. Chemical and electrical synapses were inactive at −150 ms ≤ t < 0 and enabled for t ≥ 0 (type 1 simulation). Coherence was calculated for the time interval 400 ≤ t < 500 ms. (E) Effects of synchronous application of drive to the entire network (Left) or to a subset of 20 adjacent cells (10% of the population; Right). Chemical and electrical synapses were enabled throughout the simulation, and a step-like excitatory drive was applied simultaneously to all or a subset of cells at t = 0 (type 2 simulation). Coherence was calculated for the time interval 0 ≤ t < 100 ms.