Measures of human population structure show heterogeneity among genomic regions

Abstract

Estimates of genetic population structure (F_ST) were constructed from all autosomes in two large SNP data sets. The Perlegen data set contains genotypes on ∼1 million SNPs segregating in all three samples of Americans of African, Asian, and European descent; and the Phase I HapMap data set contains genotypes on ∼0.6 million SNPs segregating in all four samples from specific Caucasian, Chinese, Japanese, and Yoruba populations. Substantial heterogeneity of F_ST values was found between segments within chromosomes, although there was similarity between the two data sets. There was also substantial heterogeneity among population-specific F_ST values, with the relative sizes of these values often changing along each chromosome. Population-structure estimates are often used as indicators of natural selection, but the analyses presented here show that individual-marker estimates are too variable to be useful. There is inherent variation in these statistics because of variation in genealogy even among neutral loci, and values at pairs of loci are correlated to an extent that reflects the linkage disequilibrium between them. Furthermore, it may be that the best indications of selection will come from population-specific F_ST values rather than the usually reported population-average values.

Publication of the Perlegen SNP data set (Hinds et al. 2005) and completion of Phase I of the International HapMap Project (The International HapMap Consortium 2005) have allowed a new perspective on the genetic structure of human populations. These two whole-genome data sets allow population genetic analyses at an unprecedented scale: Previous estimates of genetic population structure (for review, see Garte 2003) have been based on a limited number of loci and provided only average figures of quantities such as F_ST (Wright 1951) across the whole genome. The precision of previous estimates is not high, and they relate only to specific genes rather than to the region in which the markers are located. We can expect there to be some diversity in the magnitude of population structure between regions of the genome because the precise genealogy is not the same for each chromosome or part thereof, with values becoming increasingly similar the more closely linked are the regions. The genealogy can differ both by random events and by non-random events such as selection. Strong selection at a locus will induce hitch-hiking of nearby regions (Maynard Smith and Haigh 1974), leading to both a reduction in heterozygosity within populations and an increase in diversity between populations as measured by F_ST. Examination of the differences in diversity between regions therefore provides an opportunity to identify those that cannot be explained solely in terms of random sampling of the genealogy due to Mendelian segregation, variation in family size, migration, and recombination between genetic sites.

Methods for estimating F_ST from samples of a group of populations are well established (e.g., Weir and Cockerham 1984). More recently they have been discussed for estimating values separately for each of a set of populations assumed to come from a common founder, but which may differ both in their times of divergence from each other and in the sizes of the populations (Weir and Hill 2002; Shriver et al. 2004). The stochastic nature of evolution means that the actual allele frequencies in a population differ from the expected values, and the population-specific F_ST describes the variance of allele frequencies about the means for that population. Because there is only one realization of the population, the variance is estimated from the allele frequencies of that population and at least one other population. The average of the population-specific values is the usual (population-average) F_ST, and its estimate is proportional to the sample variance in allele frequencies among the sampled populations. It serves as a measure of genetic differentiation of the populations, and, in the case of population divergence being due to genetic drift, the value for each pair of populations serves as a measure of time since diverging from an ancestral population. Because there is not replication of each of the populations studied, the population-specific and population-average values are relative to the value in their ancestral population.

In this paper we compute values of F_ST from all autosomes in the Perlegen and HapMap data sets, but we use only those SNPs that were found to be segregating in all population samples within each data set. Our estimates are calculated for all markers separately and also for all markers in all the 5-Mb windows centered on each SNP in the autosomal genome. The numbers of markers used are shown in Table 1. We find substantial diversity in these measures, and we attempt to explain how much of this can be attributed to sampling of different kinds. We consider the data as a function of the number and choice of sites in the region, and as a function of the individuals that comprise the sample. We predict the variation in identity at individual regions and their covariance with other regions expected from the sampling in genealogy of the population. Further, we examine the results to reveal regions associated with known genes that have been under selection in one or more of the populations so as to consider the utility of F_ST measures in gene location or in detecting signatures of past selective events.

Table 1.

Chromosome lengths and numbers of markers segregating in all samples within a data set

	HapMap		Perlegen
Chromosome	Length (Mb)	No. markers	Length (Mb)	No. markers
1	246.022970	46,170	246.009520	83,080
2	243.358305	54,649	243.312109	92,894
3	199.162822	39,741	199.082640	66,722
4	191.635501	35,988	191.618083	72,295
5	180.745911	35,649	180.812600	72,592
6	170.669476	40,993	170.716290	69,300
7	158.406107	26,444	158.475296	60,211
8	146.291843	46,834	146.254372	62,978
9	136.309594	36,513	136.289498	39,789
10	134.894332	29,488	134.895886	52,502
11	134.291296	26,767	134.291130	49,584
12	131.958248	25,156	131.982882	46,410
13	96.174004	22,427	112.947407	45,298
14	87.047071	17,520	87.173515	36,436
15	81.776600	15,430	100.101203	30,245
16	89.881597	14,111	89.881597	28,226
17	81.701636	14,317	81.684045	23,234
18	76.111422	24,697	76.066226	33,891
19	63.583824	10,355	63.581182	13,030
20	63.584784	12,115	63.580158	23,976
21	36.954953	12,639	37.016942	18,631
22	34.764542	11,353	34.912844	13,417
All		599,356		1,034,741

Results

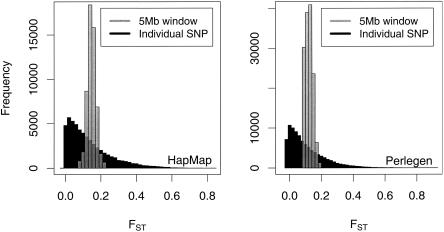
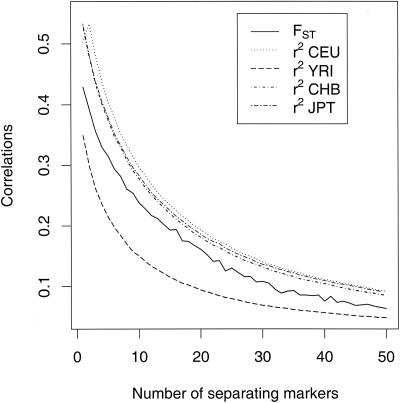
The immediate impression from a genome-wide survey of F_ST is that there is substantial variation, even among SNPs that are very close to each other. As anticipated from our earlier work (Li 1996; Weir and Hill 2002), the single-locus marker values from three or four samples have a distribution very much like the χ² distribution with two or three degrees of freedom (Fig. 1). The extreme noisiness in single-locus estimates is demonstrated in Tables 2 and 3, where the standard deviations of the values for each chromosome are seen to be about the same size as the means. The variation is even higher for the population-specific values. We have previously commented on the correlation of pairs of single-locus statistics reflecting linkage disequilibrium between those pairs (Weir et al. 2004). Specifically, the correlation for single-locus within-population inbreeding coefficients is given by r², the squared correlation of allele frequencies at those loci. There is a similar relationship for single-locus F_ST values and within-population r² values, as shown in Figure 2.

Figure 1.

Histograms of single-locus and 5-Mb window values of F_ST over the human genome.

Table 2.

HapMap single-locus F_ST values for each population and over all populations

Chromosome	CEU	YRI	HCB	JPT	All
1	.09 (.35,.04)	.12 (.41,.03)	.15 (.32,.04)	.15 (.32,.04)	.13 (.12,.02)
2	.11 (.35,.04)	.11 (.41,.04)	.16 (.31,.05)	.17 (.32,.05)	.14 (.12,.02)
3	.10 (.34,.04)	.11 (.40,.03)	.17 (.31,.04)	.17 (.31,.04)	.13 (.12,.02)
4	.11 (.34,.04)	.10 (.41,.03)	.15 (.30,.04)	.15 (.31,.04)	.13 (.12,.02)
5	.09 (.34,.04)	.13 (.39,.03)	.14 (.31,.05)	.15 (.31,.05)	.12 (.12,.02)
6	.09 (.35,.03)	.13 (.41,.03)	.14 (.31,.03)	.14 (.31,.03)	.12 (.11,.02)
7	.09 (.35,.04)	.11 (.40,.03)	.14 (.30,.04)	.15 (.32,.05)	.12 (.12,.02)
8	.10 (.33,.04)	.14 (.40,.04)	.14 (.30,.04)	.14 (.30,.04)	.13 (.12,.02)
9	.09 (.34,.03)	.11 (.40,.03)	.15 (.30,.03)	.15 (.31,.03)	.12 (.11,.02)
10	.11 (.35,.04)	.12 (.40,.03)	.14 (.31,.04)	.14 (.31,.03)	.13 (.12,.02)
11	.10 (.34,.04)	.13 (.39,.03)	.13 (.30,.03)	.12 (.30,.03)	.12 (.11,.02)
12	.09 (.36,.04)	.12 (.40,.03)	.15 (.32,.04)	.15 (.32,.04)	.13 (.12,.02)
13	.10 (.33,.03)	.11 (.40,.03)	.14 (.30,.04)	.14 (.30,.04)	.12 (.11,.02)
14	.12 (.36,.05)	.13 (.40,.02)	.13 (.30,.03)	.13 (.31,.03)	.13 (.11,.02)
15	.14 (.37,.05)	.12 (.41,.03)	.15 (.31,.05)	.15 (.32,.05)	.14 (.13,.02)
16	.10 (.35,.03)	.13 (.40,.02)	.14 (.31,.03)	.15 (.30,.03)	.13 (.11,.02)
17	.10 (.33,.04)	.14 (.40,.04)	.15 (.30,.05)	.15 (.31,.04)	.13 (.13,.03)
18	.10 (.34,.03)	.09 (.39,.03)	.14 (.29,.03)	.14 (.31,.03)	.12 (.10,.01)
19	.11 (.35,.02)	.12 (.42,.02)	.12 (.31,.02)	.14 (.32,.03)	.12 (.11,.01)
20	.09 (.33,.03)	.14 (.39,.02)	.13 (.30,.03)	.14 (.30,.04)	.12 (.11,.02)
21	.09 (.33,.03)	.13 (.39,.02)	.13 (.29,.02)	.12 (.30,.03)	.12 (.11,.01)
22	.08 (.33,.02)	.15 (.40,.03)	.14 (.31,.03)	.14 (.31,.03)	.12 (.12,.02)
All	.10 (.35,.04)	.12 (.40,.03)	.15 (.31,.04)	.15 (.31,.04)	.13 (.12,.02)

F_ST values are averaged over each chromosome. Shown in parentheses are standard deviations over each chromosome for single-SNP values and for 5-Mb window values.

(CEU) Caucasians of European descent; (YRI) Yoruba from Ibadan, Nigeria; (HCB) Han Chinese from Beijing; (JPT) Japanese from Tokyo.

Table 3.

Perlegen single-locus F_ST values for each population and over all populations

Chromosome	EA	HC	AA	AII
1	.08 (.32,.03)	.13 (.35,.04)	.09 (.34,.03)	.10 (.11,.02)
2	.09 (.32,.03)	.13 (.35,.05)	.10 (.34,.03)	.11 (.11,.02)
3	.08 (.32,.03)	.13 (.34,.04)	.08 (.33,.03)	.10 (.11,.02)
4	.09 (.32,.04)	.12 (.34,.04)	.08 (.33,.03)	.10 (.11,.02)
5	.08 (.32,.03)	.12 (.34,.04)	.10 (.34,.03)	.10 (.11,.02)
6	.08 (.31,.03)	.12 (.34,.04)	.10 (.34,.02)	.10 (.11,.02)
7	.08 (.32,.03)	.12 (.34,.03)	.10 (.34,.03)	.10 (.11,.02)
8	.09 (.32,.03)	.12 (.34,.05)	.12 (.35,.03)	.11 (.12,.02)
9	.08 (.32,.03)	.12 (.34,.04)	.09 (.33,.02)	.10 (.10,.02)
10	.10 (.33,.03)	.12 (.35,.04)	.11 (.34,.03)	.11 (.11,.02)
11	.08 (.31,.03)	.12 (.34,.04)	.09 (.33,.02)	.10 (.10,.02)
12	.08 (.33,.03)	.13 (.36,.04)	.10 (.34,.02)	.10 (.11,.02)
13	.09 (.32,.03)	.11 (.34,.04)	.11 (.34,.03)	.10 (.11,.02)
14	.09 (.33,.03)	.11 (.34,.03)	.10 (.34,.02)	.10 (.11,.01)
15	.10 (.33,.04)	.12 (.34,.03)	.09 (.33,.03)	.10 (.11,.02)
16	.08 (.31,.03)	.12 (.34,.03)	.10 (.34,.03)	.10 (.11,.01)
17	.08 (.31,.02)	.14 (.35,.04)	.10 (.34,.02)	.11 (.11,.02)
18	.09 (.32,.02)	.11 (.34,.03)	.08 (.33,.03)	.09 (.10,.01)
19	.09 (.32,.03)	.11 (.33,.02)	.09 (.33,.02)	.10 (.10,.02)
20	.10 (.31,.02)	.12 (.34,.05)	.08 (.31,.02)	.10 (.11,.02)
21	.09 (.32,.03)	.10 (.34,.03)	.09 (.33,.01)	.09 (.10,.01)
22	.08 (.31,.02)	.13 (.35,.03)	.09 (.33,.02)	.10 (.11,.01)
All	.08 (.32,.03)	.12 (.34,.04)	.10 (.34,.03)	.10 (.11,.02)

F_ST values are averaged over each chromosome. Shown in parentheses are standard deviations over each chromosome for single-SNP values and for 5-Mb window values.

(EA) European American, (HC) Han Chinese, (AA) African American.

Figure 2.

Correlations for all pairs of markers on chromosome 2 in the HapMap data. Each correlation is calculated for pairs of markers separated by a fixed number of markers (1 to 50). The F_ST correlations are between the population-average F_ST values calculated separately for each marker in the pair. The r² values (i.e., squared correlations) are for each pair of markers in each of the four HapMap samples.

The noisiness of single-locus estimates can be reduced by combining data from several adjacent markers, and we have chosen to use 5-Mb windows to clarify the graphical presentations. The distribution of these (approximately) 1000-locus values is close to normal, also as anticipated and as shown in Figure 1. Tables 2 and 3 show that chromosomal standard deviations have dropped substantially.

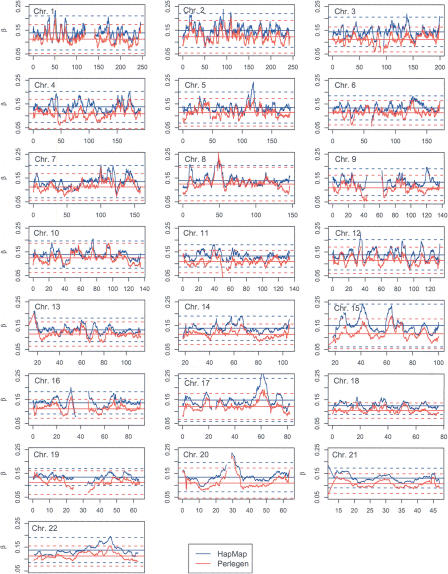
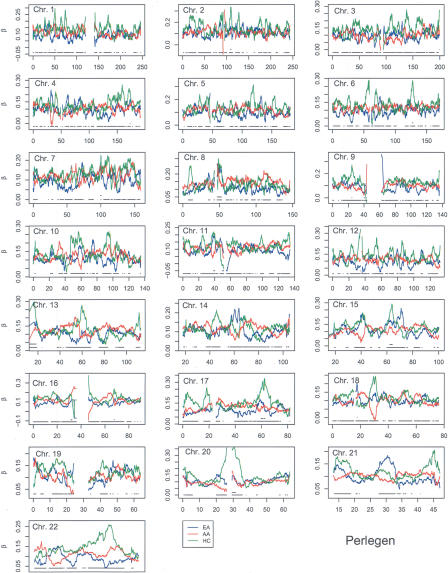
The usual studies of F_ST produce values that are, in essence, averages over the populations sampled. In Figure 3 we show the 22 autosome plots of the 5-Mb window values of F_ST that apply, as an average, to all three of the Perlegen populations or to all four of the HapMap populations. These values were calculated with the methodology of Weir and Cockerham (1984). Even for the relatively large window size of 5 Mb there is substantial variation along each chromosome, suggesting that values of F_ST are genome region-specific. This was noted by Shriver et al. (2004), who plotted individual site FST values against position, but the pooling of sites makes the heterogeneity clearer. We are struck by the similarity of the HapMap and Perlegen F_ST profiles. The HapMap values are generally higher, as might be expected since the HapMap data includes one more sample than does Perlegen, and the Perlegen African-American sample is for an admixed population with a Caucasian component. The plots in Figure 3 also show the means, plus or minus three of the standard deviations of the population-average F_ST values calculated from all 5-Mb windows for that chromosome. These lines are not intended to indicate statistical significance, but they do serve to highlight regions where F_ST values are very different from those for the rest of the chromosome.

Figure 3.

5-Mb window population-average F_ST values for HapMap (blue) and Perlegen (red) samples. (Horizontal solid lines) Chromosome mean values, (horizontal dotted lines) the chromosome means plus or minus three standard deviations.

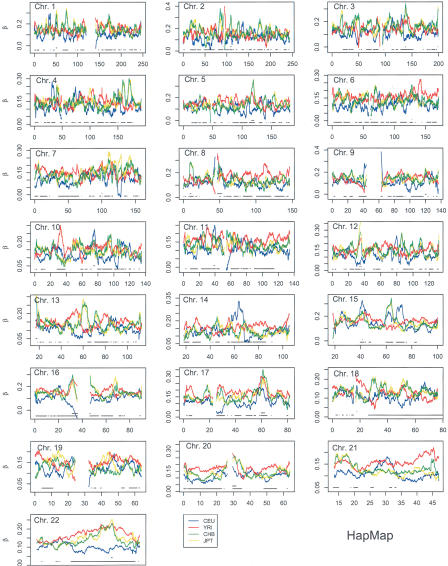
Because the usual values of F_ST are averages over populations, they may obscure signatures of past evolutionary events such as selective sweeps; so, we have also estimated population-specific values using the methodology of Weir and Hill (2002). These values show much more variation, and the very large standard deviations shown in Tables 2 and 3 indicate that single-locus values are not reliable. The 5-Mb window values, however, have coefficients of variation that are always <0.5. The plots in Figures 4 and 5 show that there are regions of considerable differences between populations, and that the ordering of population values changes along the chromosomes. We note the generally high similarity between the HapMap Han Chinese from Beijing (HCB) and Japanese from Tokyo (JPT) values, and we suggest that regions of dissimilarity, such as ∼45 Mb on chromosome 19, would be worthy of study for an explanation. There are other intriguing aspects to these plots: On chromosomes 5 and 6 the HapMap values are generally higher for Yoruba from Ibadan, Nigeria (YRI) than for Caucasians of European descent (CEU), and the Perlegen values are generally higher for African Americans (AA) than for European Americans (EA), and this pattern extends over the whole chromosome. On chromosomes 14 and 15, however, the relative sizes of these two pairs of values change along the chromosome.

Figure 4.

HapMap 5-Mb window population-specific FST values. (Lower broken line) Regions where the greatest difference between population-specific values was more than three standard deviations, (upper broken line) regions where population-average values were more than three standard deviations from the mean.

Figure 5.

Perlegen 5-Mb window population-specific F_ST values. (Lower broken line) Regions where the greatest difference between population-specific values was more than three standard deviations, (upper broken line) regions where population-average values were more than three standard deviations from the mean.

Attention must be paid to the inherent variation in F_ST values if they are to be used to detect selection. A very crude indication of when the population-specific values differ from each other is given in Figures 4 and 5, along with an indication of when the population-average values differ from the chromosome means. The broken lines at the bottom of each plot in these figures show when the largest difference between pairs of population-specific values is exceptionally large, and when population-average values are exceptionally different from the chromosome means. “Exceptionally large” means more than three standard deviations of the average values for the whole chromosome.

Because the standard deviations differ among chromosomes, a case could be made for using genome-wide standard deviations to identify exceptional values. This may lead to identification of more regions on chromosome 15, for example. There are many more regions with population differences than there are regions with values different from the mean.

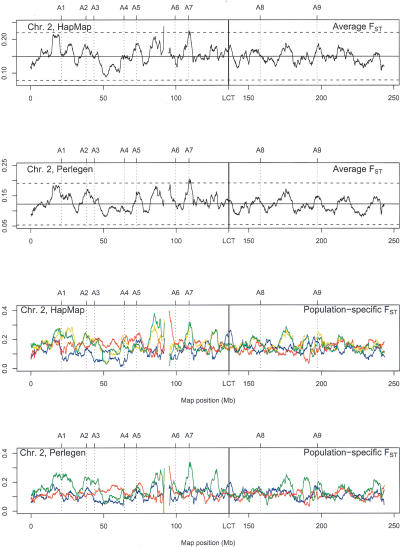
In Figure 6 we present an expanded view just for chromosome 2, and we draw attention to the region around map position 136.4 Mb, the site of the LCT gene, which encodes for the enzyme lactase-phlorizin hydrolase and is associated with adult-type hypolactasia. The population average F_ST does not show an exceptional peak, meaning that this well known example of selection may be missed in data such as those considered here, but among the population-specific values there is a clear elevation of the CEU and EA values, as might be expected for a condition that affects Caucasians (Bersaglieri et al. 2004, and references therein). This plot displays several other regions of substantial variation, with nine previously identified high values of the population-average F_ST values indicated (Akey et al. 2002 and its Supplemental Table A). These investigators identified regions of high F_ST values and regarded them as candidate genes subject to selection.

Figure 6.

Human chromosome 2 values of F_ST from HapMap and Perlegen data. For population-specific values, the HapMap populations are CEU (blue), YRI (red), CHB (green), and JPT (yellow). The Perlegen populations are EA (blue), AA (red), and HC (green). The genes A1–A9 are: A1: APOB; A2: FAM82A (formerly LOC151393); A3: THADA (formerly FLJ21877); A4: PELI1; A5: SEC15L2 (formerly SEC15B); A6: REVIL; A7: EDAR; A8: GALNT5; A9: HECW2 (formerly KIAA1301) as described in Supplemental Table A of Akey et al. (2002).

Discussion

Ascertainment

We have illustrated the substantial heterogeneity of F_ST along the human genome and we have shown the utility of estimating population-specific values. Two aspects of data ascertainment, however, mean that we cannot claim to have given a complete picture, although we can claim to have been conservative in identifying regions of elevated F_ST. In the first place, we recognize that the process whereby SNPs are discovered by typing a smaller number of individuals and then assayed in a larger sample means that SNPs with rare alleles in the discovery population are likely to be missed. The effects on population structure studies are lessened when the discovery panel is ethnically diverse, as was the case for the HapMap and Perlegen data. Otherwise, the effect of missing SNPs with small minor allele frequencies (MAF) is to lose markers where there are large values of F_ST. For the situation of populations diverging by genetic drift, for example, the value of F_ST for two populations with MAF of 0.05 and 0.15 is more than that for populations with MAF of 0.45 and 0.55, as it is inversely proportional to p(1–p). In the second place, our decision to use only SNPs that were segregating in all samples increased the chance of us not detecting large values of F_ST. Our overall picture of F_ST in the human genome is likely to miss SNPs for which the quantity is large. The similarity of the HapMap and Perlegen estimates also suggests robustness of our procedures.

Window size

We found visual appeal in using 5-Mb windows to smooth out the very high variation in F_ST at individual SNPs, and we acknowledge that this was entirely subjective. The fact that F_ST values are correlated to an extent determined by the linkage disequilibrium quantity r² might suggest that it might be preferable to base windows on values of r², or on recombination values. Such windows would have different sizes along a chromosome, but they would increase the chance of aggregating F_ST values of similar size. The method we have used has the advantage of simplicity. It also allows meaningful comparisons between different data sets, such as HapMap and Perlegen in this case, or between different subsets of populations in the same data set. It is not clear how r² based windows could be used for making comparisons between population-specific F_ST values.

Our window size was also subjective, but it does reflect our experience with different sizes. When we reduced the window size from 5 Mb to 0.5 Mb (results not shown), we saw a similar pattern on chromosome 2: The LCT peak for the population-average values was not especially pronounced, while the elevation of the CEU and EA peaks remained.

Exceptional regions

The theory presented in the Methods section and in the Appendix allows the variances in actual (parametric) values of F_ST to be predicted. With appropriate information on the evolutionary process, these variances could be calculated and used to assess when F_ST values were unusually large or small. The estimated variances for F_ST would vary with the estimated values of F_ST.

We have adopted a more expedient approach by using the standard deviation among all (window-based) values on a chromosome. The same value applies to all estimates, and the variance is inflated by regional differences in F_ST. In Figures 3, 4, 5 we have indicated when the population-average values were more than three of these standard deviations from the chromosome average, or when the range of population-specific values exceeded three standard deviations. We regard such differences as truly exceptional.

Correlated F_ST values

In Figure 2, we showed that the correlation of population-average F_ST estimates at different sites on the same chromosome was very closely approximated by r², the squared correlation of allele frequencies between sites within a population. A simple but approximate derivation provides an explanation for these results and those in Figure 2 of Shriver et al. (2004). Under a pure drift model, the changes δp_l in allele frequency p_l for one of the alleles at site l in any generation can be approximated by the normal distribution, δp_l ∼ N(0, p_l(1–p_l)/2N_e), providing the alleles are at intermediate frequency. The quantity N_e is the inbreeding effective population size. Summing over generations and assuming that the population structure parameter θ is small, then δp_l ∼ N(0, p_l(1–p_l)θ), approximately (Foulley and Hill 1999). The covariance of allele frequency change for alleles at a pair of loci due to drift is Cov(δp_l, δp_l′)= D_ll′/2N_e, where D_ll′ is the linkage disequilibrium coefficient between loci l and l′, and, hence, is consequent on both initial and new disequilibrium, D_ll′, where D_ll′ now represents the average over generations. Further, δp_l and δp_l′ are approximately multivariate normal, so it follows that Var(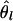) = Var(δp_l)/[p_l(1–p)] = 2 ²_l θ, Cov(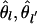) = 2D² / [p_l(1–p_l)p_l (1–^′ p_l′)], and Corr()= r². Note that the covariance of the estimates arises mainly from the disequilibrium that was present in the founder population, assuming linkage is very tight, but is estimated from that in the derived populations. Clearly the quality of the approximation improves as the time span since the populations separated decreases and the allele frequencies near 0.5. The consequence of these correlations among estimates of F_ST is that they are expected to have similar values in regions of high linkage disequilibrium. The clustering of high F_ST estimates may therefore reflect reduced recombination. Correlations higher than predicted by r² may indicate forces such as epistatic selection (Akey et al. 2004).

The theory in the previous paragraph was for the r² in the population ancestral to the sampled populations, whereas the curves in Figure 2 are for current population r²s. We note the now familiar lower value for the Yoruba population, probably reflecting the greater age of this African population, and opportunities for recombination, than the amount of time passed since the bottleneck associated with the exodus from Africa of the ancestors of other current populations.

Methods

Data

Data only from unrelated people were used. The Perlegen data set we used has data from 24 European Americans (EA), 23 African Americans (AA), and 24 Han Chinese (HC) from the Los Angeles area. The Phase I HapMap data set we used has data from 60 Caucasians of European descent (CEU), 60 Yoruba from Ibadan, Nigeria (YRI), 45 Han Chinese from Beijing (CHB), and 44 Japanese from Tokyo (JPT). Only those markers that were segregating in all three Perlegen population samples or all four HapMap population samples were used, and the numbers of markers on each chromosome are shown in Table 1. Map positions were obtained from the Perlegen publication (Hinds et al. 2005) or from the HapMap Web site, and these were used to define sliding windows: 5-Mb windows were constructed for each marker by including all markers on the same chromosome that were ≤2.5 Mb from that marker. The average number of markers per window was ∼1000, with smaller numbers within 2.5 Mb of each end of the chromosome. The “chromosome lengths” in Table 1 are the distances between the first and last markers used.

Estimates of F_ST

Our approach (Weir and Cockerham 1984; Weir and Hill 2002), consistent with that of Wright (1951), is to define parameters that describe the correlations among alleles within and between populations, and then construct estimators for those parameters. We write the sample frequency for the uth allele at the lth locus sampled from the ith population as p̃_ilu, and introduce parameters θ_i and θ_ii′, i ≠ i′ to quantify variances and covariances of these frequencies. These moments refer to variation over samples from a population (“statistical sampling”) and over replicates of the populations (“genetic sampling”). For large sample sizes only the genetic or genealogical sampling is important and

The common expected allele frequencies p_lu may be regarded as those in the population ancestral to the sampled populations. We do not make any assumptions about the evolutionary process, and so we do not assume a distributional form for allele frequencies over populations. Nor do we assume that the populations have reached an evolutionary equilibrium state. We have adopted the null assumption of equal θ values over loci, even though we expect that not to be true.

Previously we gave explicit equations for moment estimates of θ_i and θ_ii′ in the general case of unequal sample sizes from the populations (Weir and Hill 2002), and we used those equations for this study. It is helpful, however, to focus on the equal (large) sample size case and note that the estimates can then be expressed in terms of the sample heterozygosities and where p̄_lu is the average allele frequency over samples: 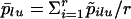. The estimates must be relative to the average between-population value θ_A:

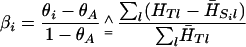(The symbol 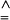means “is estimated as.”) The reference value θ_A is ∑_i≠i′ θ_ii′/r(r–1) for r samples, and this is zero for independent populations. Under a pure drift model, β_i is proportional to the time since that population diverged from the rest.

Averaging over samples gives the large-sample value of the usual moment estimate (Weir and Cockerham 1984):

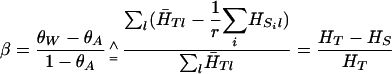This is the average within-population coancestry θ_W = ∑_i θ_i/r relative to the average between-population-pair coancestry θ_A. We refer to the estimates of β as either 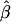or as F_ST. Estimates of β_i are written as .

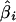Sampling properties of F_ST

We have shown substantial variation in F_ST values over the human genome, but we need to consider the sampling properties of these estimates before seeking biological explanations. There have been two principal ways of generating sampling distributions in the literature. Some authors have simulated the histories either of the populations (and drawn samples from those) or of the samples, but this requires knowledge of past evolutionary processes and of the values of parameters such as mutation and recombination rates. The coalescent simulation approach also has an inherent equilibrium assumption. Various numerical resampling or permutation procedures have also been invoked. Permuting population labels is appropriate for testing hypotheses that there is no variation among populations (F_ST = 0), but in our case we are more interested in comparing the non-zero values among populations.

We have previously advocated bootstrapping over loci (Dodds 1986), under the assumption that each locus has been subjected to the same genealogical history. As we are interested in detecting differences among F_ST values in different genomic regions, however, we now modify that recommendation to apply to resampling loci in each region—assuming that there are large numbers of markers per region as is the case for the 5-Mb regions we have reported on here.

We have the advantage of having had access to two large data sets, and so, to some extent, we have replicate populations for our study. The fact that there was good overall agreement in the two sets of estimates and identification of regions of interest, even though neither data set had especially large numbers of individuals, suggests that sampling variation for windows-based estimates is not of major concern. We would, however, place little weight on single-locus estimates.

Genealogical variation

There is a parametric value of F_ST for each population or set of populations, but there is also variation about this expected value. Cockerham and Weir (1983) discussed this variation within the framework of regarding θ as the probability of two alleles in the same population being identical by descent (ibd). For large samples, they showed that the variance of the actual value of θ in a population is (Δ–θ²), where Δ is the probability that any two pairs of alleles are ibd. This variance is quite general, but it can be expressed entirely in terms of θ under approximations for specific models. For the pure drift case, Robertson (1952) showed Δ ≈ 1–[24(1–θ)–10(1–θ)³ + (1–θ)⁶]/15, so that the variance in actual θ is θ³(1–θ)(10–5θ + θ²)/15. For populations at an evolutionary equilibrium, when allele frequencies satisfy a Dirichlet distribution over populations, Δ = θ²(1 + 5θ)/[(1 + θ)(1 + 2θ)], and the variance becomes θ³(1–θ)/[(1 + θ)(1 + 2θ)]. For a value θ = 0.10, the standard deviations from these formulations become 0.03. In the Appendix we give a more detailed discussion, along with numerical values for populations subject only to genetic drift. Standard deviations for 5-Mb windows of 1000 markers seem to be of the order of 0.01.

The empirical standard deviations of the population-average F_ST values for 5-Mb windows over all loci on a chromosome are ∼0.02. These reflect the variation in F_ST parametric values over windows and so are higher than those appropriate for a particular window. As a matter of expedience, we regarded F_ST values as being exceptionally extreme if they differ by more than three of these empirical standard deviations from the chromosome mean value, and pairs of population-specific values as being exceptionally distinct if they differ from each other by more than three standard deviations. We do not claim that these have any specific statistical significance, but we do expect that these exceptional values are beyond those that might be accounted for by variation at neutral loci.

Appendix

Predicted variance of actual identity

Although we wish to draw inferences on the basis of F_ST estimates, we recognize that the actual parametric value of this quantity varies about its predicted value. There is variation inherent in the genealogies of the individuals sampled and in the loci scored. We have addressed this variation previously (Weir et al. 1980; Cockerham and Weir 1983), and here we present a more direct formulation of those results. This formulation allows us to investigate the effects of sample size and window length under simplifying assumptions.

We regard the underlying parameter θ of population structure as the probability that any two alleles at one locus in a population are identical by descent (ibd). The actual identity θ^a(not the quantity F_ST calculated from allele frequencies) among all pairs of alleles, within and between a sample of n individuals from that population, has a variance over individuals and over populations with the same history of

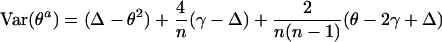where γ is the probability that any three alleles in the population are ibd and Δ is the ibd probability for any two pairs of alleles. The variance of actual identity averaged over m loci is

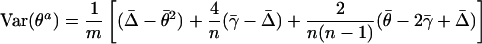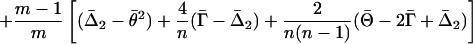Here Θ, Γ, and Δ₂ are the two-locus analogs of θ, γ, and Δ, and the bars indicate averages over all m loci or all m(m–1) pairs of loci.

The identity by descent framework is the natural one for considering populations evolving under the effects of drift alone. For a population of size N mating at random, the one-locus identity measures change between successive generations t, t + 1 according to, for example, Weir (1994)

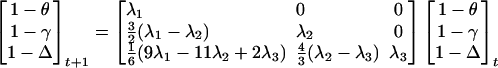where λ₁ = (2N–1)/2N, λ₂ = (2N–2)λ₁/2N, λ₃ = (2N – 3)λ₂/2N.

The two-locus ibd measures for loci with a recombination fraction c satisfy the recurrence equations (Weir and Cockerham 1974), where Θ*(c) = Θ(c) + 2θ–1, Γ*(c) = Γ(c) + 2θ–1, Δ*(c)₂ = Δ(c)₂ +2θ–1.

For m equally spaced loci in a window of length d, suppose the recombination fraction between adjacent markers is the map

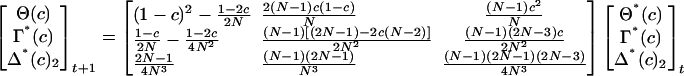distance d/m between them. There are m(m–1)/2 pairs of loci in the window, and (m–j) of these pairs are j loci apart (j = 1 for adjacent markers). The average two-locus measure X̄(X = Θ, Γ, Δ*) for the window is

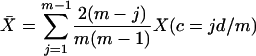In Table A1 we show some numerical values for the standard deviations of actual identity for pairs of alleles within and among n = 50 individuals for windows of sizes m = 1,10, 100, and 1000 markers when adjacent markers are 5 kb apart (and have recombination fraction c =5 × 10^–6). We derived these values by iterating the one- and two-locus identity measures, for a population of size N = 10,000 that was initially completely at non-identity, for as many generations as necessary to reach specified values of θ. The standard deviations would be smaller for larger population sizes, and vice versa.

Table A1.

Predicted standard deviations of actual identity

	Number of loci
θ	m = 1	m = 10	m = 100	m = 1000
.05	.0136	.0132	.0089	.0036
.10	.0303	.0271	.0155	.0057
.15	.0494	.0416	.0215	.0077
.20	.0699	.0558	.0270	.0094
.25	.0909	.0693	.0319	.0110
.30	.1120	.0817	.0362	.0123
.35	.1325	.0928	.0398	.0134
.40	.1521	.1023	.0427	.0143
.45	.1702	.1101	.0450	.0150
.50	.1865	.1162	.0465	.0154