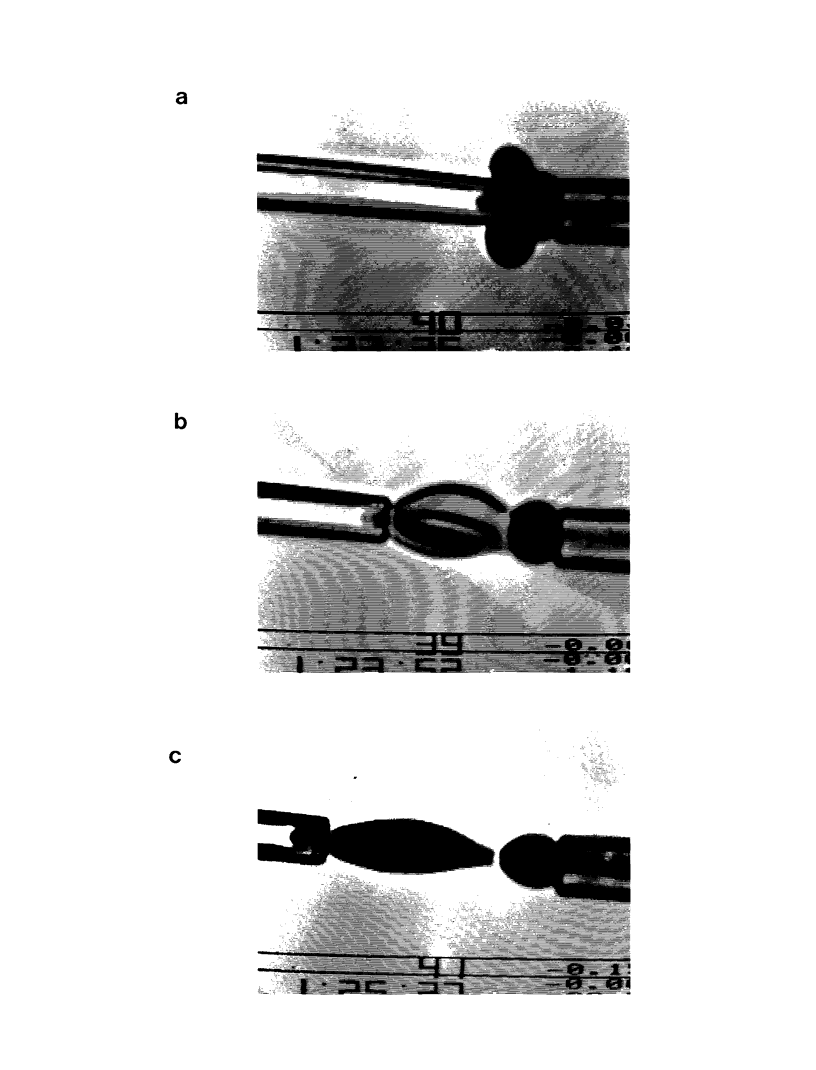
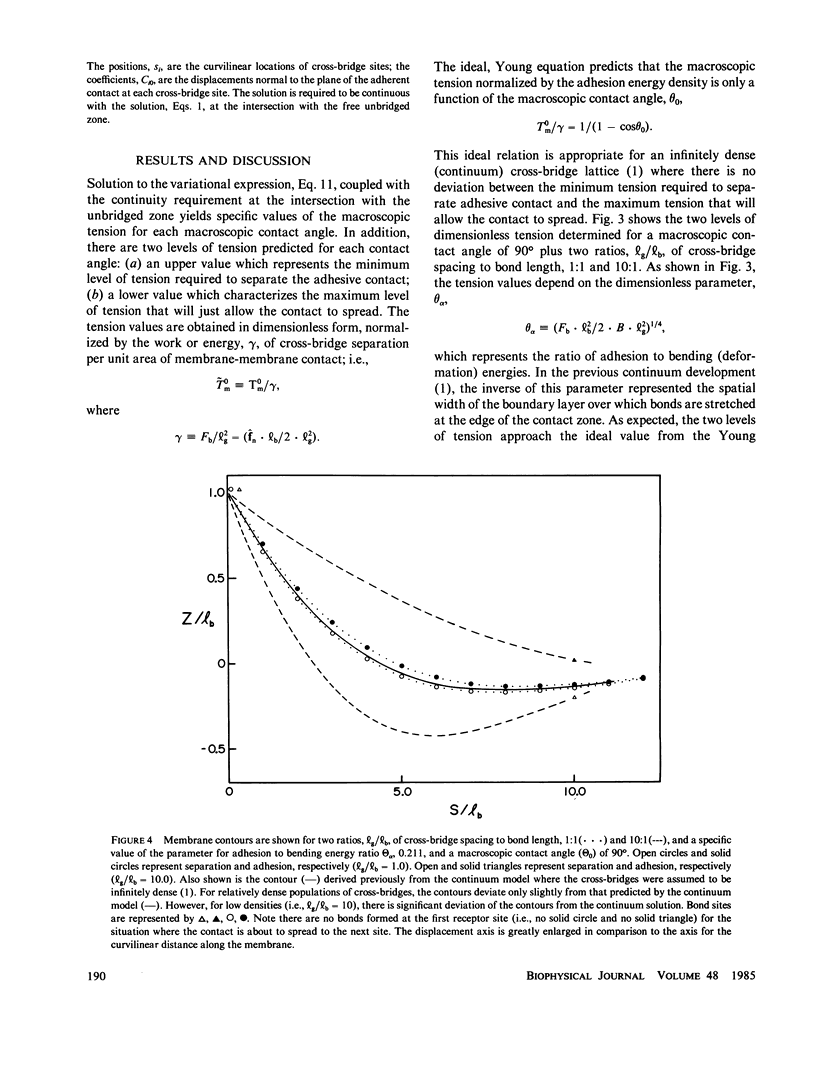
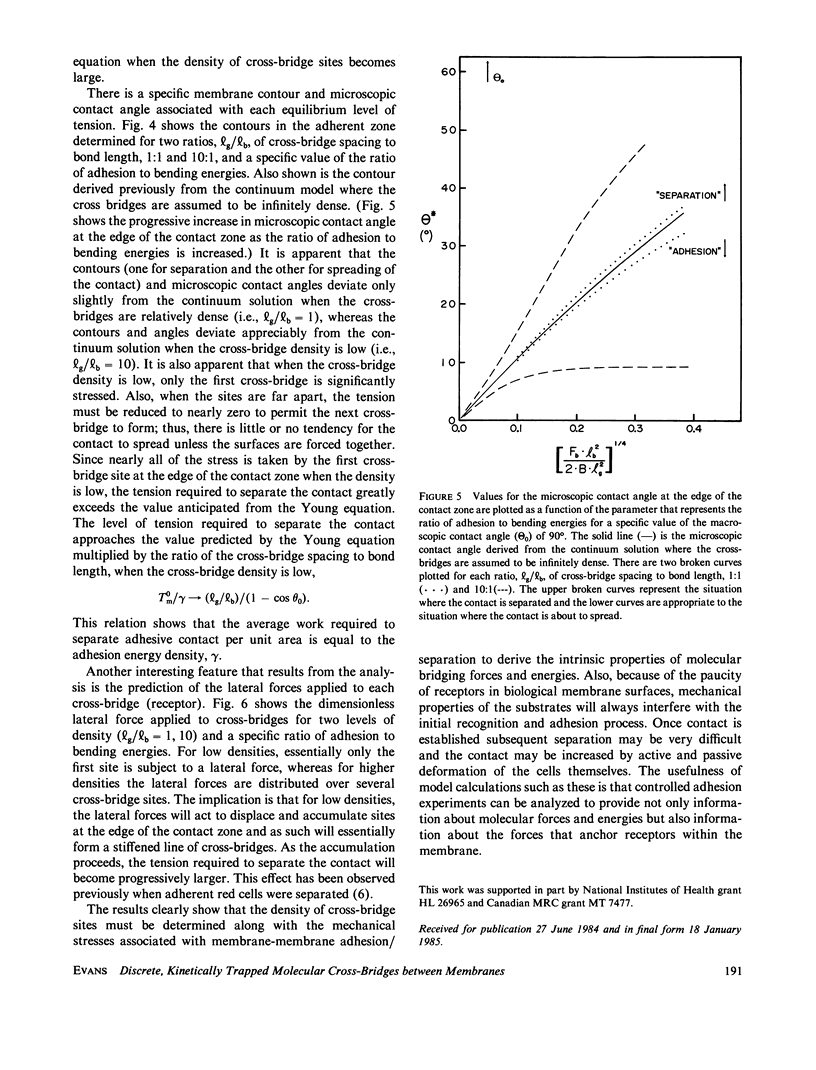
Abstract
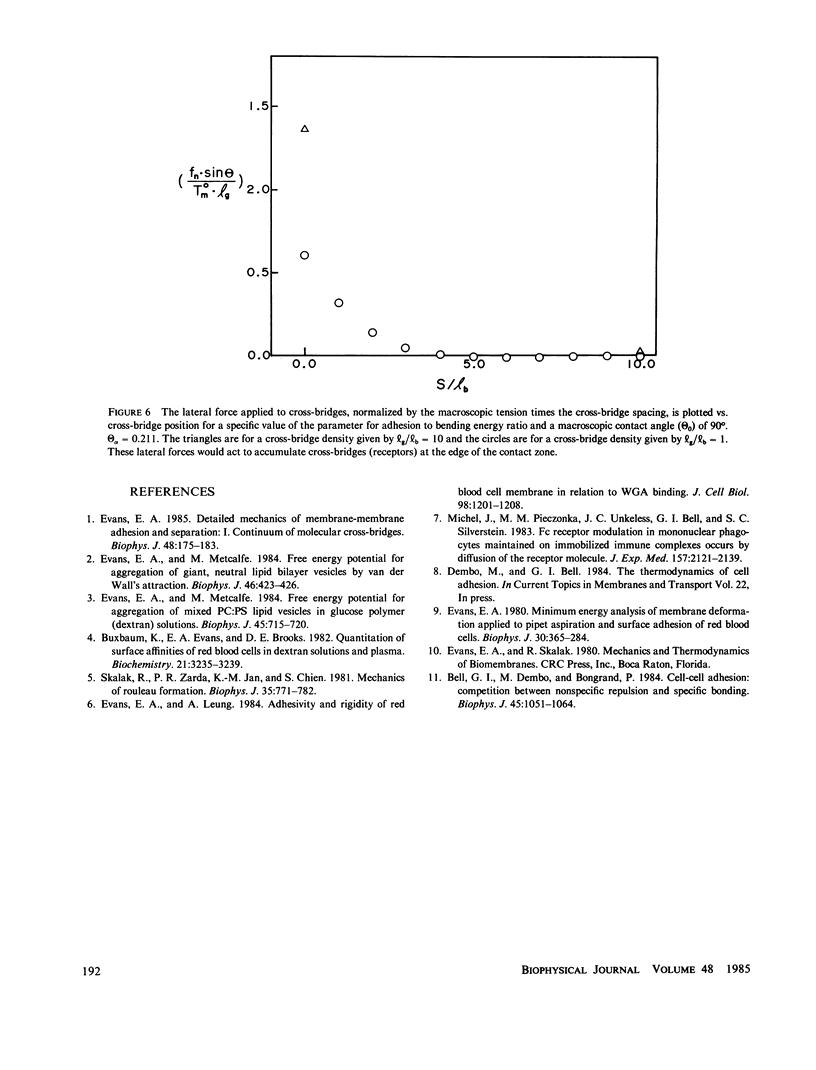
In general, membrane-membrane adhesion involves specific molecular binding and cross-bridging reactions. The ideal, classical view is that near equilibrium the forces required to separate adhesive contacts are essentially equal to those induced in the membrane when the contact is formed. In contrast to the classical view, experimental observations often show that negligible levels of tension are induced by the adhesive contact even though the tension required to separate the contact is large enough to rupture the membrane. The deviation in tension levels associated with contact formation and separation appears to be due to the sparse distribution of strong molecular cross-bridges. Here, the mechanics of membrane-membrane adhesion and separation is developed for the case of discrete, kinetically trapped cross-bridges. The solution is obtained by numerical computation of the membrane contour that minimizes the total free energy (membrane elastic energy of deformation plus cross-bridge energies) in the contact zone. This solution is matched with the analytical solution for membrane stresses and geometry derived for the adjacent, unbridged zone. The results yield specific values of the macroscopic tension applied to the membrane in the plane region away from the contact zone and the microscopic angle at the edge of the contact zone. Two disparate values of the macroscopic tension are found: (a) the minimum tension required to separate the adherent membranes; and (b) the maximum tension induced in the membranes when the contact is formed (i.e., the level of tension at which the contact will just begin to spread). The results show that the deviation between these two tensions can be very large and depends strongly on the surface density of cross-bridges. In addition, the results provide an estimate of the restraining forces that anchor receptors within the plane of the membrane.
Full text
PDF



Images in this article
Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Bell G. I., Dembo M., Bongrand P. Cell adhesion. Competition between nonspecific repulsion and specific bonding. Biophys J. 1984 Jun;45(6):1051–1064. doi: 10.1016/S0006-3495(84)84252-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buxbaum K., Evans E., Brooks D. E. Quantitation of surface affinities of red blood cells in dextran solutions and plasma. Biochemistry. 1982 Jun 22;21(13):3235–3239. doi: 10.1021/bi00256a032. [DOI] [PubMed] [Google Scholar]
- Evans E. A. Detailed mechanics of membrane-membrane adhesion and separation. I. Continuum of molecular cross-bridges. Biophys J. 1985 Jul;48(1):175–183. doi: 10.1016/S0006-3495(85)83770-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans E. A. Minimum energy analysis of membrane deformation applied to pipet aspiration and surface adhesion of red blood cells. Biophys J. 1980 May;30(2):265–284. doi: 10.1016/S0006-3495(80)85093-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans E., Leung A. Adhesivity and rigidity of erythrocyte membrane in relation to wheat germ agglutinin binding. J Cell Biol. 1984 Apr;98(4):1201–1208. doi: 10.1083/jcb.98.4.1201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans E., Metcalfe M. Free energy potential for aggregation of giant, neutral lipid bilayer vesicles by Van der Waals attraction. Biophys J. 1984 Sep;46(3):423–426. doi: 10.1016/S0006-3495(84)84039-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans E., Metcalfe M. Free energy potential for aggregation of mixed phosphatidylcholine/phosphatidylserine lipid vesicles in glucose polymer (dextran) solutions. Biophys J. 1984 Apr;45(4):715–720. doi: 10.1016/S0006-3495(84)84213-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michl J., Pieczonka M. M., Unkeless J. C., Bell G. I., Silverstein S. C. Fc receptor modulation in mononuclear phagocytes maintained on immobilized immune complexes occurs by diffusion of the receptor molecule. J Exp Med. 1983 Jun 1;157(6):2121–2139. doi: 10.1084/jem.157.6.2121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skalak R., Zarda P. R., Jan K. M., Chien S. Mechanics of Rouleau formation. Biophys J. 1981 Sep;35(3):771–781. doi: 10.1016/S0006-3495(81)84826-6. [DOI] [PMC free article] [PubMed] [Google Scholar]