Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1974 May;14(5):412–431. doi: 10.1016/S0006-3495(74)85924-2

Concentration Polarization in an Ultrafiltering Capillary

William M Deen, Channing R Robertson, Barry M Brenner
PMCID: PMC1334548  PMID: 4836036

Abstract

Concentration polarization, the accumulation of retained solute next to an ultrafiltering membrane, elevates osmotic pressure above that which would exist in the absence of polarization. For ultrafiltration in a cylindrical tube, use of the radially averaged solute concentration results in an underestimate of osmotic pressure, yielding an effective hydraulic permeability (k) less than the actual membrane hydraulic permeability (km). The extent to which k and km might differ in an ultrafiltering capillary has been examined theoretically by solution of the momentum and species transport equations for idealized capillaries with and without erythrocytes. For diameters, flow velocities, protein concentrations and diffusivities, and ultrafiltration pressures representative of the rat glomerular capillary network, results indicate that the effects of polarization are substantial without erythrocytes (k/km = 0.7) and persist, but to a lesser extent, with erythrocytes (k/km = 0.9), the reduction in polarization in the latter case being due to enhanced plasma mixing. In accord with recent experimental findings in rats, k is found to be relatively insensitive to changes in glomerular plasma flow rate.

Full text

PDF
413

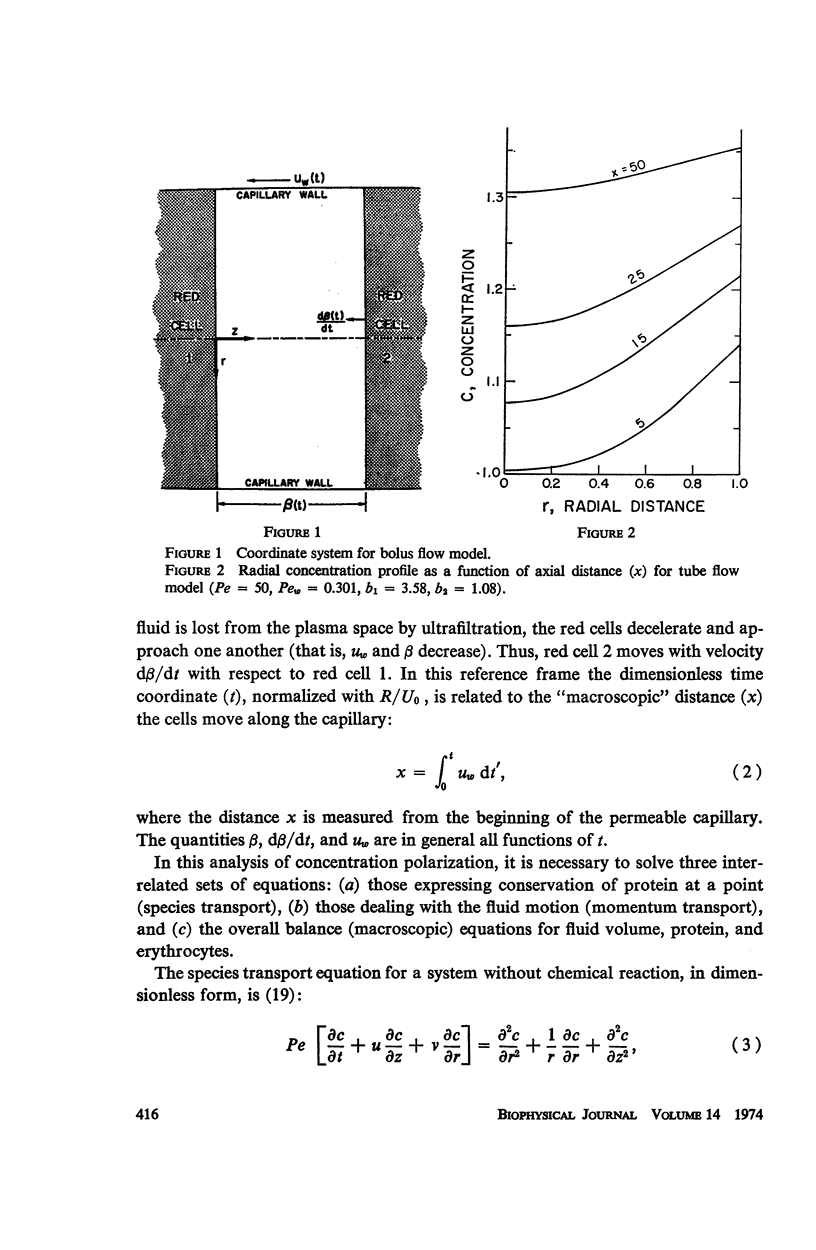
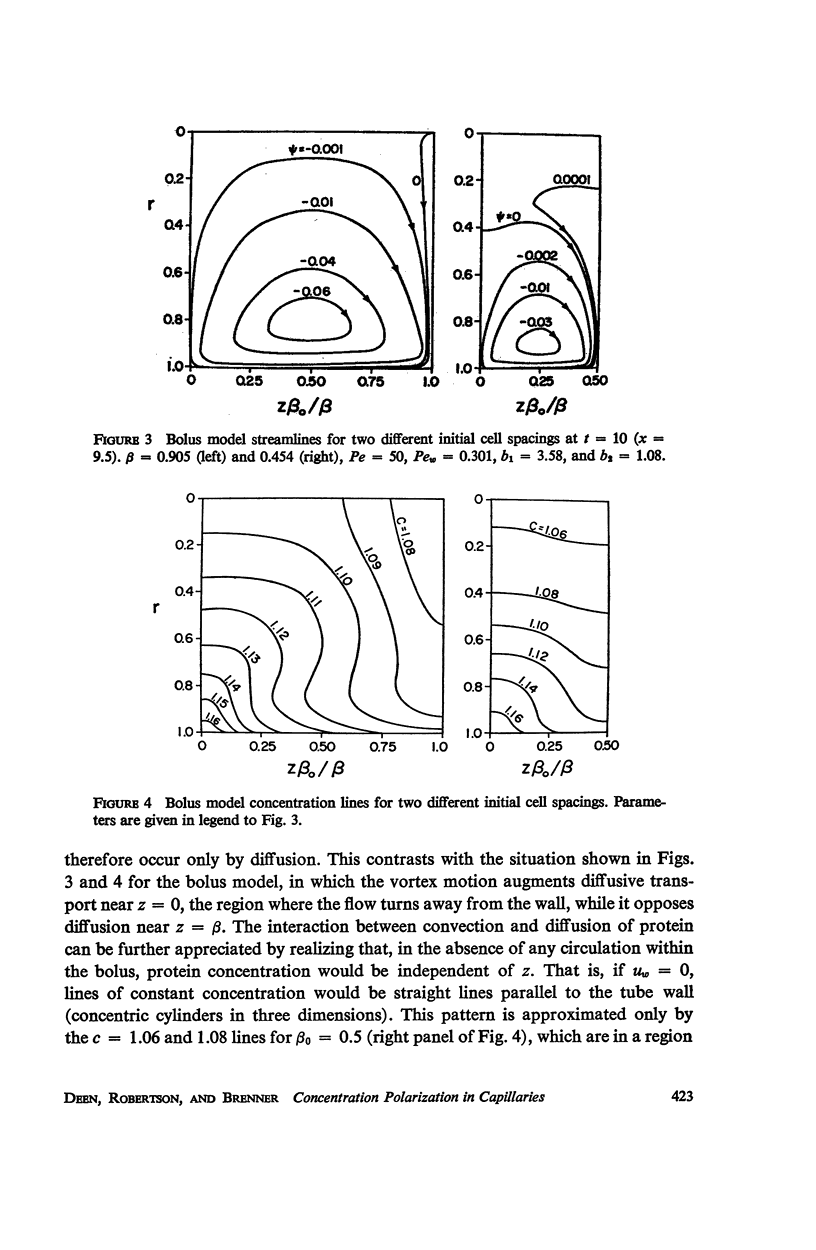
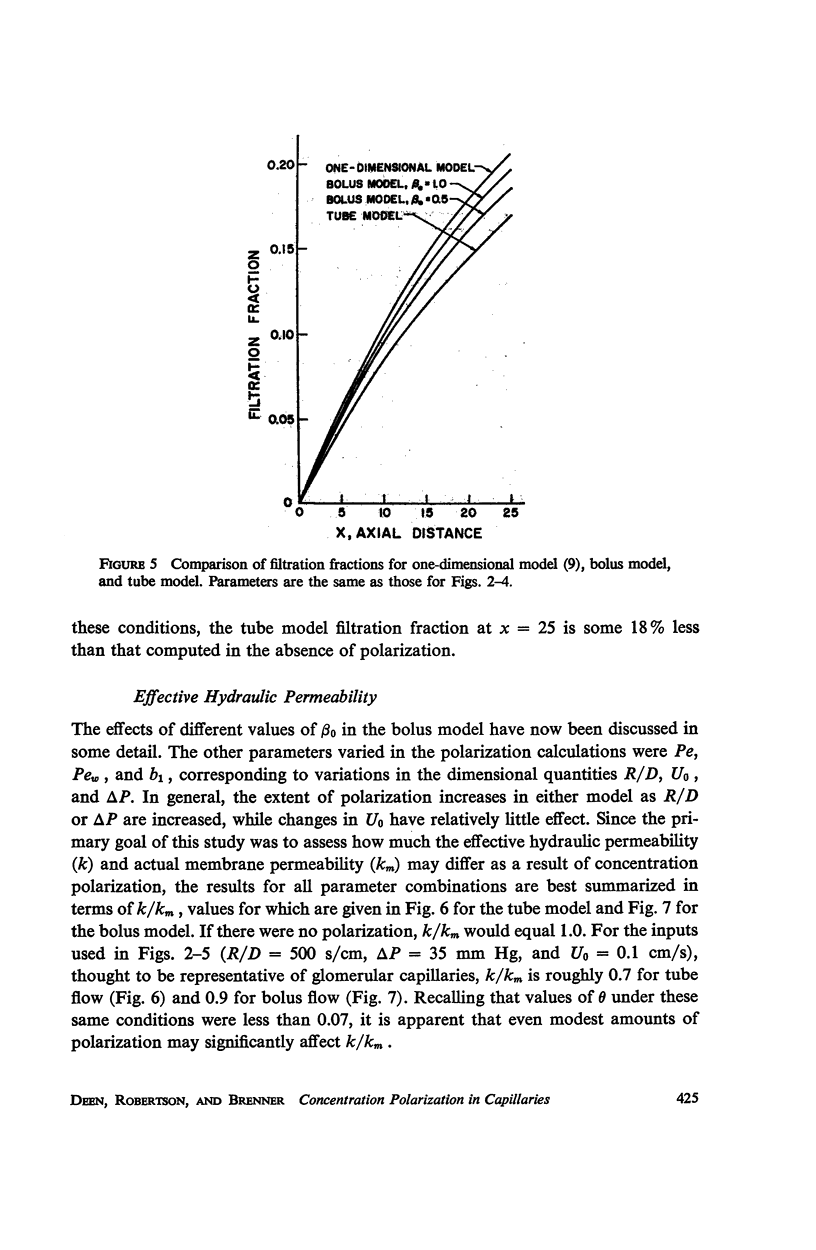
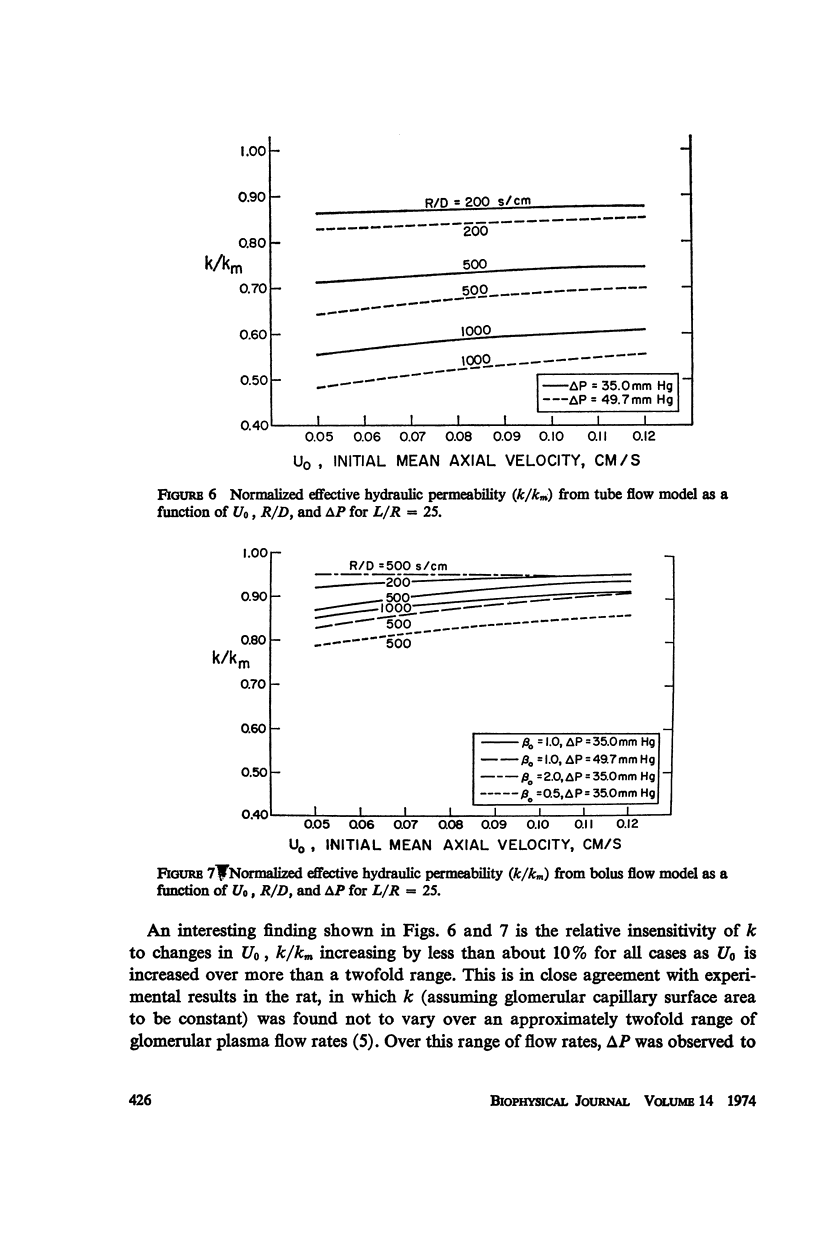
Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Aroesty J., Gross J. F. Convection and diffusion in the microcirculation. Microvasc Res. 1970 Jul;2(3):247–267. doi: 10.1016/0026-2862(70)90016-6. [DOI] [PubMed] [Google Scholar]
  2. Brenner B. M., Troy J. L., Daugharty T. M., Deen W. M., Robertson C. R. Dynamics of glomerular ultrafiltration in the rat. II. Plasma-flow dependence of GFR. Am J Physiol. 1972 Nov;223(5):1184–1190. doi: 10.1152/ajplegacy.1972.223.5.1184. [DOI] [PubMed] [Google Scholar]
  3. Brenner B. M., Troy J. L., Daugharty T. M. The dynamics of glomerular ultrafiltration in the rat. J Clin Invest. 1971 Aug;50(8):1776–1780. doi: 10.1172/JCI106667. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bugliarello G., Hsiao G. C. A mathematical model of the flow in the axial plasmatic gaps of the smaller vessels. Biorheology. 1970 Jun;7(1):5–36. doi: 10.3233/bir-1970-7102. [DOI] [PubMed] [Google Scholar]
  5. Daugharty T. M., Ueki I. F., Mercer P. F., Brenner B. M. Dynamics of glomerular ultrafiltration in the rat. V. Response to ischemic injury. J Clin Invest. 1974 Jan;53(1):105–116. doi: 10.1172/JCI107527. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Deen W. M., Robertson C. R., Brenner B. M. A model of glomerular ultrafiltration in the rat. Am J Physiol. 1972 Nov;223(5):1178–1183. doi: 10.1152/ajplegacy.1972.223.5.1178. [DOI] [PubMed] [Google Scholar]
  7. Deen W. M., Robertson C. R., Brenner B. M. A model of peritubular capillary control of isotonic fluid reabsorption by the renal proximal tubule. Biophys J. 1973 Apr;13(4):340–358. doi: 10.1016/S0006-3495(73)85989-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Deen W. M., Troy J. L., Robertson C. R., Brenner B. M. Dynamics of glomerular ultrafiltration in the rat. IV. Determination of the ultrafiltration coefficient. J Clin Invest. 1973 Jun;52(6):1500–1508. doi: 10.1172/JCI107324. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Eriksson E., Myrhage R. Microvascular dimensions and blood flow in skeletal muscle. Acta Physiol Scand. 1972 Oct;86(2):211–222. doi: 10.1111/j.1748-1716.1972.tb05327.x. [DOI] [PubMed] [Google Scholar]
  10. Fitz-Gerald J. M. Mechanics of red-cell motion through very narrow capillaries. Proc R Soc Lond B Biol Sci. 1969 Nov 18;174(1035):193–227. doi: 10.1098/rspb.1969.0088. [DOI] [PubMed] [Google Scholar]
  11. Fung Y. C. Blood flow in the capillary bed. J Biomech. 1969 Oct;2(4):353–372. doi: 10.1016/0021-9290(69)90013-x. [DOI] [PubMed] [Google Scholar]
  12. Gross J. F., Aroesty J. Mathematical models of capillary flow: a critical review. Biorheology. 1972 Dec;9(4):225–264. doi: 10.3233/bir-1972-9402. [DOI] [PubMed] [Google Scholar]
  13. Intaglietta M., Richardson D. R., Tompkins W. R. Blood pressure, flow, and elastic properties in microvessels of cat omentum. Am J Physiol. 1971 Sep;221(3):922–928. doi: 10.1152/ajplegacy.1971.221.3.922. [DOI] [PubMed] [Google Scholar]
  14. Keller K. H., Canales E. R., Yum S. I. Tracer and mutual diffusion coefficients of proteins. J Phys Chem. 1971 Feb 4;75(3):379–387. doi: 10.1021/j100673a015. [DOI] [PubMed] [Google Scholar]
  15. Lee J. S. Analysis on diffusion and convection of protein in tissue. J Appl Physiol. 1972 Feb;32(2):254–256. doi: 10.1152/jappl.1972.32.2.254. [DOI] [PubMed] [Google Scholar]
  16. Lew H. S., Fung Y. C. The motion of the plasma between the red cells in the bolus flow. Biorheology. 1969 Aug;6(2):109–119. doi: 10.3233/bir-1969-6205. [DOI] [PubMed] [Google Scholar]
  17. Lin K. L., Lopez L., Hellums J. D. Blood flow in capillaries. Microvasc Res. 1973 Jan;5(1):7–19. doi: 10.1016/s0026-2862(73)80003-2. [DOI] [PubMed] [Google Scholar]
  18. Maddox D. A., Deen W. M., Brenner B. M. Dynamics of glomerular ultrafiltration. VI. Studies in the primate. Kidney Int. 1974 Apr;5(4):271–278. doi: 10.1038/ki.1974.36. [DOI] [PubMed] [Google Scholar]
  19. PROTHERO J., BURTON A. C. The physics of blood flow in capillaries. I. The nature of the motion. Biophys J. 1961 Sep;1:565–579. doi: 10.1016/s0006-3495(61)86909-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Robertson C. R., Deen W. M., Troy J. L., Brenner B. M. Dynamics of glomerular ultrafiltration in the rat. 3. Hemodynamics and autoregulation. Am J Physiol. 1972 Nov;223(5):1191–1200. doi: 10.1152/ajplegacy.1972.223.5.1191. [DOI] [PubMed] [Google Scholar]
  21. Smaje L., Zweifach B. W., Intaglietta M. Micropressures and capillary filtration coefficients in single vessels of the cremaster muscle of the rat. Microvasc Res. 1970 Jan;2(1):96–110. doi: 10.1016/0026-2862(70)90055-5. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES