Relating Cell Killing to Inactivation of Critical Components

Abstract

In this paper I relate the loss of CFU following a life-threatening treatment to the inactivation of critical components. Equations are used to calculate the loss of CFU following isothermal and temperature-scanning treatments, and the results are discussed in relation to differential scanning calorimetry of bacteria.

The precise mechanism by which heat kills prokaryote and eukaryote cells is still not known despite decades of scientific, medical, and commercial interest (4). However, there is a widespread view that this killing is caused by thermal denaturation of critical targets in the cell, and this is an underlying theme of much previous theory (for reviews see references 5 and 13). This notion became directly testable with the discovery that differential scanning calorimetry could lay out in sequence the complex series of denaturation events that takes place when cells are heated (7, 17). Crucially, this technique allows cell death and the thermal denaturation of components to be superimposed in order to identify which components denature simultaneously with cell death and which do not (8, 11, 12, 14). Initially, cell death curves were calculated from previously reported D and z values (9), but in subsequent studies workers measured death rates and differential scanning calorimetry curves in the same experiments. The research described in the accompanying paper (10) is the latest research in this line of experiments and also measured D and z values for cell inactivation under isothermal and temperature-scanning conditions. These papers show that the most sensitive part of the ribosome denatures simultaneously with cell death in all mesophilic and thermophilic vegetative bacteria examined so far. However, there are numerous copies of ribosomes in each cell (∼10,000 copies) (2), and the observed kinetics of cell death, which do not show a shoulder region that is long enough, are incompatible with existing critical target theory (4).

In the analysis described below I modified critical target theory by analyzing the survival of cells following a life-threatening treatment (which is undefined and could be heat treatment, irradiation, bathing in antibiotic or cytotoxin, or other chemical procedure, such as deletion or insertion of a gene). I focused on what is essential for the life of the cell rather than on the effect of a particular treatment and recognized that some components of the cell are vital to its existence, while others are useful but not essential. The theory thus incorporates the recent discovery of essential and nonessential genes (3). It also incorporates the molecular nature of the action of antibiotics and reexamines how cell killing is affected by the numbers of copies of critical components within the cell. The analysis provides a general equation for cell survival following critical damage to critical components and then calculates cell survival as a function of time for isothermal heat damage and as a function of temperature for temperature scanning. Existing critical target theory is a special case of this general equation. I start by defining terms and then apply some mathematics.

A critical component of the cell is defined here as a component whose number of functioning copies within the cell must remain above a critical level (which may be zero) for the cell to survive or reproduce. Furthermore, if the number of functioning copies of a critical component falls below the critical level, the cell cannot increase the number of copies by resynthesis. For example, ribosomes are required for the cell to survive and reproduce, and new ribosomes cannot be resynthesized by a cell devoid of ribosomes. Thus, ribosomes are critical components. Other examples of critical components include DNA, the cell envelope, and RNA polymerase.

Critical components have one or more essential functions. Essential functions are functions that must be carried out by the cell for it to survive or reproduce. Critical damage is defined here as irrecoverable damage that stops any essential function of a critical component. Thus, for example, deletion of an essential gene from the genome is critical damage, while deletion of a nonessential gene is not, since cells without essential genes are not viable but cells without nonessential genes may be viable (3). Here the critical component is the DNA, and the essential function is provision of the genetic code required to make the protein or nucleic acid that is essential for a viable cell.

In order for damage to a cell to be lethal, at least one critical component must be critically damaged at or above a critical intensity. Consider, for example, a single prokaryote cell that may contain 10,000 or more ribosomes (2). If just one of these ribosomes were critically damaged, would that be sufficient for cell death to ensue? Surely the remaining thousands of noncritically damaged ribosomes could cope with the required essential function of protein synthesis. At the other extreme, if all copies were critically damaged, the cell clearly could not survive. At either of these extremes or somewhere between them lies the critical intensity, the amount of critical damage that is required for the cell to die or fail to reproduce. Mathematically, the probability of a cell surviving and being capable of reproduction after critical damage to the jth critical component is P_j(r_j), where r_j is the number of copies of the jth critical component that are not critically damaged.

To summarize, for a cell to die or fail to reproduce, I hypothesize that one or more critical components must be critically damaged and that the probability of surviving critical damage to a critical component depends on the number of copies that the cell contains which are not critically damaged (or equally, the number of copies that are critically damaged).

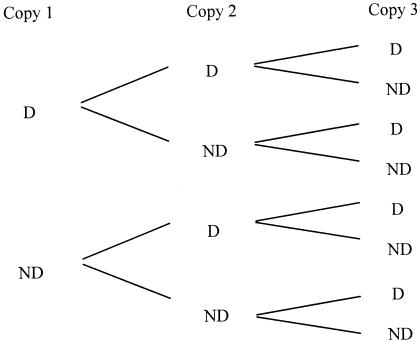
Armed with this vocabulary, we can analyze the life or death response of an individual cell to a life-threatening treatment. Let us suppose that the treatment critically damages one of the critical components, while the other critical components in the cell are not critically damaged. Let the probability, in the population of cells as a whole, that a particular critical component (a ribosome, for example) is critically damaged be indicated by x. The probability that it is not critically damaged is therefore 1 − x. In an individual cell, each copy of the critical component can be arbitrarily labeled as follows: copy 1, copy 2, … .copy n. By drawing probability trees for possible outcomes, we can calculate the probabilities for different outcomes in a cell containing n copies (Fig. 1):

FIG. 1.

Probability tree for a cell containing three copies of a particular critical component. Starting from the two possible results for the first copy (it may be critically damaged [D] or not critically damaged [ND]), we can construct the set of all possible results for the second and third copies. If the probability that the critical component is critically damaged is x, the diagram can be used to show that the probability that all copies are critically damaged is x³. The probability that two copies are critically damaged and one copy is not critically damaged is 3x²(1 − x). The probability that one copy is critically damaged and two copies are not critically damaged is 3x(1 − x)², and the probability that all three copies are not critically damaged is (1 − x)³.

In this way we find that the probability that the cell contains (n − r) copies that are critically damaged and r copies that are not critically damaged is

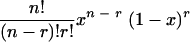(1)

We suppose that the probability that an individual cell will survive [P(r)] depends on the number (r) of copies per cell that are not critically damaged. The proportion of cells surviving the treatment (S) is therefore:

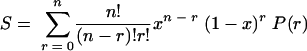(2)

Equation 2 relates to critical damage of only one critical component. If more than one critical component is damaged, the proportion of survivors is the product of the fractions surviving due to critical damage to each of the critical components:

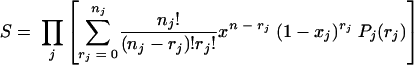(3)

While equation 3 is the more general equation, for simplicity I restrict further consideration (see Appendix) to equation 2, the case where only one type of critical component is critically damaged.

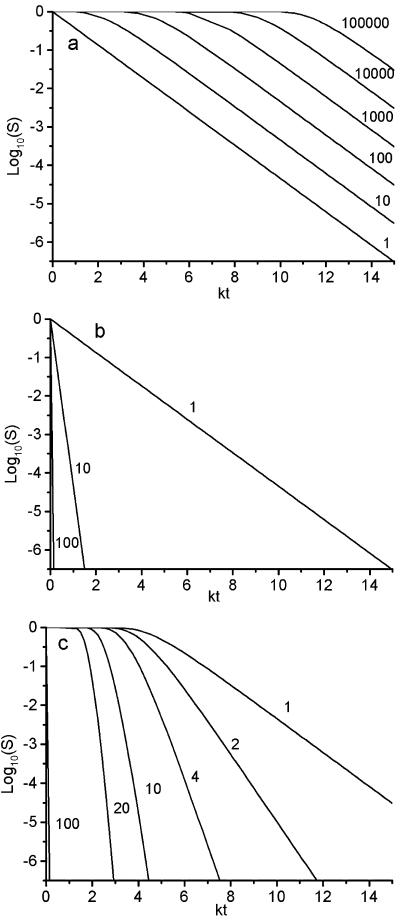
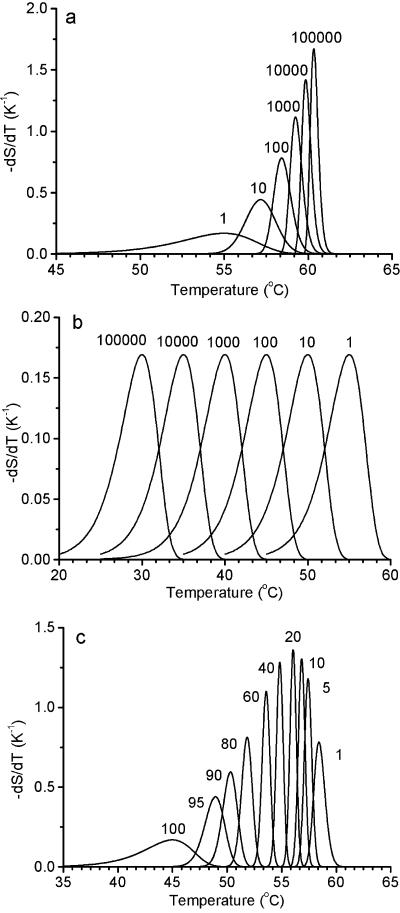
Figures 2 and 3 show calculations of S using equation 2 for various values of the functions x and P (see Appendix). Figure 2 shows the results for isothermal solutions. Figure 3 shows the results for −dS/dT under temperature-scanning conditions. The differential is calculated to make the results comparable with differential calorimetry results and to show how the shape and position of the peaks are affected by n and P. Figures 2a and 3a show the results for solutions at one extreme value for the probability function P (representing the condition that the cell will survive if at least one copy of the critical component is not critically damaged). Figures 2b and 3b show the results for solutions at the other extreme (that a cell will survive only if all copies of the critical component are not critically damaged). Figures 2c and 3c show the results for intermediate values. In order to compare cell death (S) with critical component damage (x), it is important to know that 1 − x is given by the line n = 1 in Fig. 2a and 2b and dx/dT = −dS/dT when n = 1 in Fig. 3a and 3b. It is also important to note that these lines (n = 1) also represent cell survival, irrespective of the value of n, if P(r) = r/n (see Appendix).

FIG. 2.

Calculations using equation A3 of the proportion of cells surviving an isothermal heat treatment in which the probability of critical damage to a critical component is x = 1 −exp(−kt). (a) Plot assuming that all copies of a critical component must be critically damaged for a cell to die (R = 1). The numbers indicate the number of copies per cell (n). The line for n = 1 also represents 1 − x. (b) Plot assuming that no copies of a critical component must be damaged for the cell to survive (R = n). The numbers indicate the number of copies per cell (n). (c) Plot assuming that the total number of copies of the critical component per cell is 100. The number (R) of copies that are not critically damaged per cell is indicated beside each line.

FIG. 3.

Calculations for the rate of decline of surviving cells during temperature scanning based on differentiating equation A3. (a) Plot assuming that all copies of a critical component must be critically damaged for a cell to die (R = 1). The numbers indicate the number of copies per cell (n). The line for n = 1 also represents the rate of critical damage of the critical component, dx/dT. (b) Plot assuming that no copies of a critical component must be damaged for the cell to survive (R = n). The numbers indicate the number of copies per cell (n). (c) Plot assuming that the total number (n) of copies of the critical component per cell is 100. The number (R) of copies that are not critically damaged per cell is indicated beside each line. The fraction of critical components that are critically damaged is x = 1 − exp[−exp(0.4606T − 25.333)], representing a process with a D value of 0.5 min at 55°C and a z value of 5°C for scanning at a rate of 10°C/min (9).

The results of this study show that the loss of CFU following heating may precede, lag behind, or coincide with the loss of the active critical component, depending on the form of the function P(r) and the number of copies of the critical component in each cell. In the study described in the accompanying paper, coworkers and I found that the isothermal death kinetics of campylobacters conform more or less to an exponential decline, with no marked initial shoulder. The z value of the process measured isothermally, approximately 6°C, was found to be the same when it was measured kinetically under conditions of constantly rising temperature, and the D values measured kinetically and isothermally were also similar magnitudes. On the basis of critical target theory, we might have concluded from these results that there is only one copy (or relatively few copies) of the critical target per cell (see the condition n = 1, R = 1 in Fig. 2 and 3). However, the results of the study showed that inactivation of a heat-sensitive critical component present at large numbers of copies per cell could be responsible for the results described above under certain conditions [e.g., P(r) = r/n]. This might occur if enzyme degradation of ribosome 16S RNA (16), which is controlled by the highly temperature-dependent unfolding of the 30S ribosome subunit, were the ultimate cause of cell death, as suggested by Tolker-Nielsen and Molin (15). Mathematically, this and other possibilities are allowed for in the theory described above by leaving P(r) undefined. The actual form of the relationship needs to be investigated experimentally. In the meantime, it is still not possible to identify the critical damage that leads to cell death in heat-treated Campylobacter cells, even though heat denaturation of the most sensitive parts of the ribosome is coincident with the loss of CFU. On a more fundamental level, the theory also poses the following questions: what components of the cell are critical components, what are their essential functions, and how can critical damage be inflicted? Answers to these questions could inform developments in such different fields as antibiotics, cancer treatment, and food safety.

APPENDIX

To calculate S from equation 2, we need to know n, x, and P. n is just an integer, the number of copies of the critical component per cell. x is also relatively simple. For a first-order rate process under isothermal conditions:

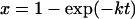(A1)

and for a temperature scan in which the temperature increases at a constant rate (m) (9),

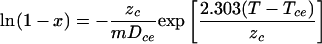(A2)

where D_ce is the time required to reduce the number of noncritically damaged critical components by 10-fold at temperature T_ce and z_c is the increase in T_ce required to reduce D_ce by 10-fold (note that these values are different from the D and z values for cell inactivation, which are simply indicated by D and z, without subscripts).

P(r) is more complicated. It depends on the critical component and the nature of the critical damage. I consider here just two types of function. (i) The first type of function is a step function, P(r) = 1, r ≥ R and P(r) = 0, r < R. In this case, the proportion of cells surviving is given by the probability that a cell contains R or more copies that are not critically damaged

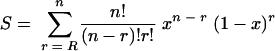(A3)

Two special cases are of interest. When R = 1

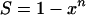(A4)

This is the critical target criterion (1, 6); i.e., cells die when all copies of the critical component have been critically damaged. The other special case is when R = n,

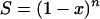(A5)

(ii) The second type of function is a linear function, P(r) = r/n. In this case the probability that a cell will survive is proportional to the number of copies that are not critically damaged that it contains. When this is inserted in equation 2,

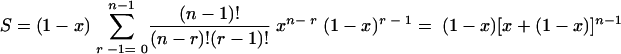(A6)

i.e.,

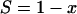(A7)

Thus, the proportion of survivors is the same as the proportion of copies of the critical component that are not critically damaged, irrespective of the total number of copies per cell. Another way of looking at this is that cells survive as if there were only one copy of the critical component per cell (put n = 1 in equation A4 or A5) and the two processes (cell death and critical damage to the critical component) are coincident in both isothermal and temperature-scanning conditions.