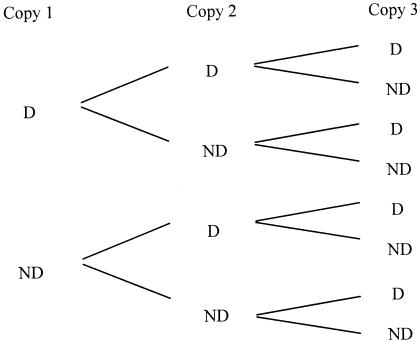
FIG. 1.
Probability tree for a cell containing three copies of a particular critical component. Starting from the two possible results for the first copy (it may be critically damaged [D] or not critically damaged [ND]), we can construct the set of all possible results for the second and third copies. If the probability that the critical component is critically damaged is x, the diagram can be used to show that the probability that all copies are critically damaged is x3. The probability that two copies are critically damaged and one copy is not critically damaged is 3x2(1 − x). The probability that one copy is critically damaged and two copies are not critically damaged is 3x(1 − x)2, and the probability that all three copies are not critically damaged is (1 − x)3.