Intercellular coupling amplifies fate segregation during Caenorhabditis elegans vulval development

Abstract

During vulval development in Caenorhabditis elegans, six precursor cells acquire a spatial pattern of distinct cell fates. This process is guided by a gradient in the soluble factor, LIN-3, and by direct interactions between neighboring cells mediated by the Notch-like receptor, LIN-12. Genetic evidence has revealed that these two extracellular signals are coupled: lateral cell-cell interactions inhibit LIN-3-mediated signaling, whereas LIN-3 regulates the extent of lateral signaling. To elucidate the quantitative implications of this coupled network topology for cell patterning during vulval development, we developed a mathematical model of LIN-3/LIN-12-mediated signaling in the vulval precursor cell array. Our analysis reveals that coupling LIN-3 and LIN-12 amplifies cellular perception of the LIN-3 gradient and polarizes lateral signaling, both of which enhance fate segregation beyond that achievable by an uncoupled system.

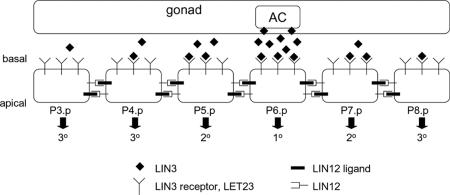
Vulval development in Caenorhabditis elegans involves the spatially coordinated commitment of vulval precursor cells (VPCs) toward distinct cell fates, labeled primary (1°), secondary (2°), and tertiary (3°) fates (Fig. 1). This patterning is guided by an EGF-like soluble factor, LIN-3, that is produced by a centrally positioned anchor cell (AC). LIN-3 activates an EGF receptor (LET-23)-mediated signal transduction pathway in the VPCs that is required for 1° and 2° cell fates; in the absence of LIN-3, all VPCs assume the default, 3° fate (1).

Fig. 1.

Spatial patterning of VPCs in C. elegans. The AC in the gonad releases LIN-3, which distributes across the linear array of VPCs (P3.p-P8.p). This factor binds its receptor LET-23 on the basal surface of the precursor cells and provides an inductive signal for fate specification. The interplay between the inductive signal (LIN-3:LET-23 complexes) and lateral coupling between neighboring cells mediated by LIN-12 and its ligands specifies P3.p-P8.p cells to three distinct cell fates (1°, 2°, and 3°).

The dose of LIN-3 is a critical determinant of cell fate. In animals in which all VPCs but one are ablated, the intact VPC chooses a cell fate depending on its relative position to the AC: when close to the AC, the VPC chooses 1° fate, and, when distal from the AC, it chooses the 3° fate. At intermediate position, the VPC chooses a 2° fate (1). Indeed, a gradient in LIN-3 signaling has been observed indirectly in vivo by using a sensitive reporter of LIN-3-mediated transcriptional activity (2). These observations strongly support the notion that LIN-3 acts as a morphogen, a soluble factor whose spatial concentration gradient influences cell fate choices (3, 4).

In addition to the LIN-3 signal, direct communication between neighboring cells involving the Notch-like receptor (LIN-12) and its ligands drives cell patterning. In organisms lacking LIN-12, VPCs fail to commit to 2° fate, producing only 1°/3° cell fates (5). Meanwhile, in mutant organisms with hyperactive inductive, LET-23-mediated signals, VPCs acquire not only 1° fates but also 2° fates. In fact, an intriguing alternating pattern of 1° and 2° cells (e.g., 2°1°2°) is observed, suggesting that commitment to 1° fate forces its direct neighbors to acquire 2° fate via a lateral “inhibitory” signal (6). These and other observations suggest a sequential model wherein LIN-3 inductive signal is essential only to promote 1° cell fate, which in turn stimulates 2° fate choice via a direct, lateral signal to its neighbors.

Resolving the relative importance of the LIN-3 gradient (morphogen model) and the lateral signal (sequential model) is challenged by the fact that these two extracellular signals are coupled through an intracellular signaling network (7). LIN-3 binds LET-23 and produces intracellular signals via a canonical Ras-mitogen-activated protein kinase signaling pathway (8). Activation of the mitogen-activated protein kinase (MPK), MPK-1, stimulates the production of LIN-12 ligands and the endocytosis of LIN-12 (9-11). Thus, the inductive LIN-3 signal influences the extent to which each VPC sends out and receives lateral signal by modulating the expression of LIN-12 ligand and LIN-12, respectively. LIN-12, in turn, affects the extent to which each VPC is responsive to the inductive signal: LIN-12 stimulates the transcription of negative regulators of the LIN-3-mediated Ras signaling pathway (2, 12).

While the biochemical details of the intracellular molecular mechanisms coupling LIN-3 and LIN-12 are being elucidated, the quantitative effects of this network topology remain unclear. Because lateral signaling couples the signaling network in each VPC to that of its neighbors, it is expected to influence how each VPC responds to its local LIN-3 concentration. Conversely, the local LIN-3 concentration will impact how effectively a particular VPC receives and sends lateral signals. Here, we develop and analyze a mathematical model of LIN-3/LIN-12-mediated signaling to elucidate quantitatively how this network topology achieves spatially patterned cell fate specification.

Results and Discussion

Improved Gradient Perception. Two observations indicate that LIN-3 performs as a prototypical morphogen whose spatial gradient determines cell fate patterning. First, cell fate is sensitive to LIN-3 dose (1). Second, a gradient in LIN-3 concentration has been observed indirectly in vivo (2). These observations raise the question of why cells seemingly guided to pattern formation by a morphogen gradient further require a lateral signaling mechanism.

To begin to address this issue, we examined how lateral coupling affects the perception of the extracellular gradient in the inductive signal LIN-3. The response of a simplified, two-cell system to gradients in LIN-3 concentration was simulated by specifying the amount of inductive signal for neighboring cells (I₁ for cell 1 and I₂ for cell 2) (Fig. 2). To quantify how a gradient in extracellular LIN-3 concentration (I₁/I₂) is converted into a gradient in LIN-3-mediated intracellular MPK signal, we defined a gradient comparator (Q) as

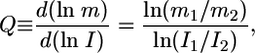[1]

where m₁ and m₂ are the steady-state fraction of activated MPK-1 in cells 1 and 2, respectively. Note that Q is undefined when there is no gradient in input (i.e., I₁/I₂ = 1). When the relative spatial gradient in LIN-3 translates into exactly the same relative spatial gradient in MPK-1^*, the value of Q is 1. When the spatial gradient in intracellular signal is attenuated relative to the gradient in extracellular stimulus, the value of Q is <1; in contrast, when the MPK-1^* gradient is amplified relative to the extracellular LIN-3 gradient, the value of Q is >1.

Fig. 2.

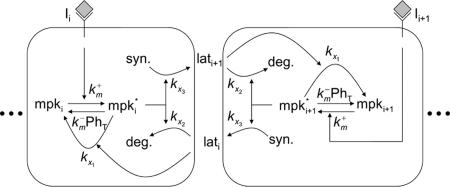
Model schematic. A pair of interacting cells, i and i+1, is shown; longer cell arrays are simulated by adding similar modular cells to the array. The inductive signal I_i activates MPK-1 in each cell i with rate constant 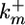. Constitutive phosphatases Ph deactivate MPK-1^* with rate constant 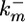. The inductive signal up-regulates the lateral signal in the neighboring cell with rate constant k_x3 and down-regulates it in the same cell with rate constant k_x2. In turn, the lateral signal in each cell deactivates MPK-1^* with rate constant k_x1.

In the absence of lateral coupling (i.e. χ = 0), between neighboring cells, the gradient comparator (Q°) is given by

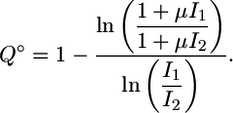[2]

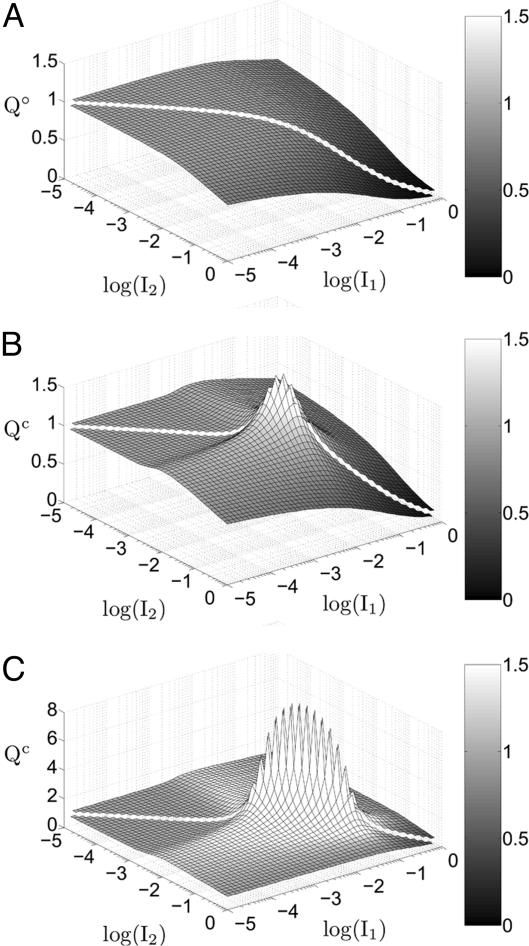
This expression reveals two regimes of perceiving gradients in inductive signal. For sufficiently low I₁ and I₂ (specifically, I₁ << μ^-1 and I₂ << μ^-1), the value of Q° is nearly 1. Thus, in this input domain, a gradient in extracellular signal is converted to a near-equivalent gradient in intracellular signal. For relatively higher values of I₁ and I₂, Q° decreases below 1, indicating that a gradient in extracellular signal is converted into a shallower gradient in intracellular signal. At these higher values of input, relative changes in input do not translate into the same relative change in intracellular signal because of a saturation of available inactive MPK-1 molecules. Fig. 3A depicts these two regimes of gradient perception in an uncoupled system. For I₁ = 10^-1 and I₂ = 10^-2 with μ^-1 = 0.05, Q° is ≈0.61, indicating that a 10-fold difference in input produces only a 4-fold difference in intracellular signal. Even significant differences in extracellular input result in considerably milder differences in intracellular signal, suggesting that establishing steep gradients in extracellular signal may be an inadequate mechanism for assuring distinct cell fate choices in an uncoupled system.

Fig. 3.

Gradient amplification in coupled systems. The value of the gradient comparator (Q) was determined for a wide range of inductive signals in a two-cell system that was uncoupled [χ = 0 (A)] or coupled at two different strengths [χ = χ°(B) and χ = 10 χ°(C)]. The color bar denotes the relationship between the grayscale and the value of the gradient comparator. (B and C) Only in the presence of lateral coupling, the value of the gradient comparator exceeds 1, indicating gradient amplification in that subdomain of inductive signals. The extent of gradient amplification increases in the presence of greater lateral coupling (compare B and C).

In contrast, a system coupled by lateral signaling displays gradient amplification. The value of the gradient comparator for a coupled system (Q^c) exceeds one in a subdomain of inductive signals (Fig. 3B). In this region, a gradient in extracellular signal is amplified to produce a steeper gradient in intracellular MPK-1^* signal. For example, maximum gradient amplification occurs at I₁ = 0.0091 and I₂ = 0.0072 (equivalent to 910 and 720 LIN-3:LET-23 complexes per cell, respectively). For this combination of inductive signals, the value of Q^c is 1.8, indicating that the ≈30% difference in inductive signal is magnified to ≈50% difference in intracellular MPK-1^* activity between neighboring cells. For low to moderate coupling, an increase in the strength of coupling further enhances the extent of gradient amplification (Fig. 3C). For the aforementioned combination of inductive signals, Q^c improves to 9.0 when the value of χ is increased 10-fold, corresponding to a ≈725% disparity in intracellular MPK-1^* activity, whereas the extracellular signals still differ by only ≈30%. These results demonstrate that lateral coupling substantially sharpens the perception of an extracellular gradient in LIN-3, overcoming an inherent limitation of uncoupled systems.

The underlying cause of amplified perception of the LIN-3 gradient involves the establishment of a countergradient in lateral signaling. In analytical terms, to achieve gradient amplification (i.e., Q^c > 1), the following condition must hold:

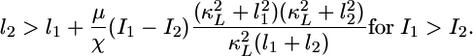[3]

That is, the lateral signal in cell 2 must be sufficiently greater than the lateral signal in cell 1, yielding a gradient that is in direct opposition to the gradient in inductive signal (I₁ > I₂). Thus, as in the context of a metabolic network (13), gradient amplification requires the presence of two competing contributions, one inductive (LIN-3) and the other inhibitory (lateral signal), whose spatial profiles run counter to each other.

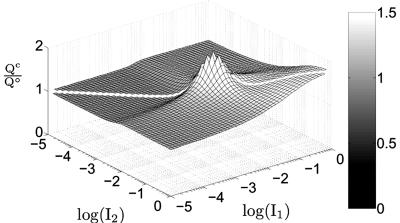
Even in regions of the input domain where gradient amplification does not occur (Q^c < 1 in Fig. 3 B and C), lateral coupling still provides a robust and significant advantage over an uncoupled system in perceiving a morphogen gradient. For example, for I₁ = 10^-1 and I₂ = 10^-2, Q^c is ≈0.85, whereas the gradient comparator for an uncoupled system, Q°, is 0.61. Thus, lateral coupling offers ≈40% improvement in perceiving this particular gradient in extracellular signal when compared with the uncoupled system. In fact, Fig. 4 shows that in the entire domain of inductive signals, the coupled system outperforms an uncoupled system in perceiving a gradient in inductive signal. Thus, the gradient comparator for a coupled system (Q^c) is greater than or equal to Q° for all combinations of inductive signals. In mathematical terms, we find that lateral coupling improves the perception of a gradient in inductive signal, i.e., Q^c > Q°, if

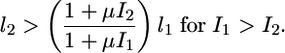[4]

Fig. 4.

Coupled systems robustly outperform uncoupled systems in gradient sensing. The ratio of the gradient comparator for coupled systems (Q^c) to that of uncoupled systems (Q°) is plotted for a wide range of inductive signals in a two-cell system. Lateral coupling was maintained at its reference value (χ = χ°). The ratio Q^c:Q° ≥ 1 in the entire domain of inductive signals.

The above criterion is less stringent than that required for gradient amplification (Eq. 3), suggesting that it may be satisfied over a broader range of model parameters. In fact, the coupled system meets this condition, or the associated equality, for any choice of model parameter values (see Supporting Text, which is published as supporting information on the PNAS web site). Thus, our model predicts that lateral coupling robustly enables better, or at least equivalent, gradient perception as an uncoupled system, with the added advantage that for a subset of inductive signals meeting condition (Eq. 3), lateral coupling amplifies the external gradient. These predictions are currently being tested in wild-type (coupled) and mutant (uncoupled) worms in which the gradient in MPK-1^* is monitored by using an egl-17 transcriptional reporter.

What determines whether the perception of LIN-3 gradient is amplified? We have stated that an opposing gradient in lateral signal is required (Eq. 3). However, even in the absence of coupling (χ = 0), a gradient in the inductive signal LIN-3 produces a countergradient in lateral signal (Fig. 5A), owing to MPK-1-mediated regulation of lateral signaling (Fig. 2, arrows marked k_x2 and k_x3). In systems, such as the R3-R4 fate specification in Drosophila, this morphogen-induced bias in lateral signal is then magnified via a feedback loop intrinsic to the Notch-Delta signaling system (14). However, the polarization of lateral signals between neighboring cells has no consequence for the interpretation of the morphogen gradient in these systems.

Fig. 5.

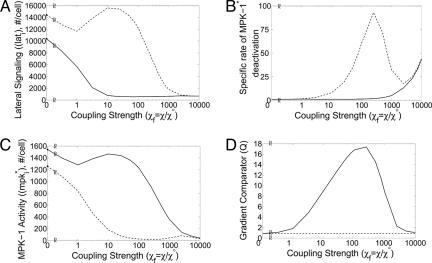
Factors contributing to coupling-mediated gradient amplification. (A) Lateral signal in cell 1 (solid) and in cell 2 (dashed) is shown as a function of lateral coupling strength. (B) The specific rate of MPK-1^* deactivation is plotted as a function of coupling strength for cell 1 (solid) and 2 (dashed). The specific rate of MPK-1^* deactivation is the rate of MPK-1^* deactivation normalized by the amount of MPK-1^*, and, according to Eq. 8, it is given by 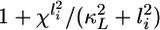. (C) The amount of MPK-1^* in cells 1 (solid) and 2 (dashed) is plotted as a function of lateral coupling strength. (D) The value of the gradient comparator in a coupled system Q^c,max (solid) and uncoupled system Q° (dashed) are shown for varying lateral coupling strength. Calculations were performed at I₁ = 0.0091 and I₂ = 0.0072, the combination of inductive signals that yielded maximum Q^c when lateral coupling strength is χ_f = χ/χ° = 1 (Fig. 3B).

Here, vulval development in C. elegans appears to be unique. Experimental evidence suggests that the Notch-Delta-like lateral signaling system is not self-propelled by an intrinsic positive feedback (15). Rather, in the presence of coupling (χ > 0), lateral signal deactivates MPK-1 (Fig. 2, arrow marked k_x1). Thus, a gradient in inductive LIN-3 signal sets a disparity in lateral signal (Fig. 5A), and in a coupled system, the latter provides a disparity in the specific driving force for MPK-1^* deactivation (Fig. 5B). The net effect is that the cell receiving smaller inductive signal receives greater lateral signal and possesses greater specific activity for MPK-1^* deactivation (Fig. 5 A and B, cell 2). These disparities render the MPK-1 activity in this cell more sensitive to the strength of coupling. Thus, as the value of χ is increased, the MPK-1 activity decreases in the cell distal from the LIN-3 signal, whereas the cell proximal to the inductive signal is less affected (Fig. 5C). However, at extremely high values of χ, lateral signal-mediated deactivation of MPK-1 dominates, even in the cell receiving the higher inductive signal (Fig. 5B). Thus, the disparity in MPK-1 activity shrinks (Fig. 5C), thereby eliminating the key element supporting a gradient in lateral signal. In the absence of a lateral signaling gradient at extremely high χ (Fig. 5A), the MPK-1 gradient is determined entirely by the LIN-3 gradient, as would be the case in an uncoupled system. Thus, for extremely high χ, the perception of the LIN-3 gradient becomes equivalent to that of an uncoupled system (Fig. 5D).

Our analysis shows that intercellular coupling via Delta-Notch signaling alters the way VPCs perceive the LIN-3 morphogen gradient. This gradient appears steeper when read as intracellular MPK-1 activity. We propose that this mechanism for enhancing the perception of the gradient reveals a paradigm for spatial patterning that contrasts other developmental contexts wherein the extracellular morphogen gradient itself is made steeper or otherwise reshaped to guide patterning. Examples of the latter include the establishment of Gurken and Spitz morphogen gradients during Drosophila egg development (16, 17) or Hedgehog and Wingless morphogen gradients during Drosophila wing disk patterning (18).

Enhancing the gradient in intracellular perception without altering the extracellular morphogen gradient raises the possibility that one mode of perception (e.g., the MPK pathway) is amplified, whereas other parallel signals generated by the morphogen mirror the external gradient. This differential perception may help to modularize the developmental purpose of a morphogen while leaving parallel signals available to mediate other critical cellular/organismal functions. Indeed, such pleiotropic roles for soluble factors is not uncommon because most ligands, including EGF, often stimulate several parallel signaling pathways and concomitantly affect a range of cell functions.

Fate Plane. Our analysis demonstrates that lateral coupling enhances the perception of the extracellular LIN-3 gradient in a two-cell model system. In addition, experimental evidence suggests that lateral signaling plays a more direct role in specifying cell fates (19). In the absence of lateral signaling, the 2° fate is not observed, although VPCs acquire 1° and 3° fates. Furthermore, in mosaic experiments where P5.p and P7.p cells lack the receptor for LIN-3, these cells still acquire 2° fate, suggesting that the lateral LIN-12-mediated signal may confer this fate independently, provided that the inductive LIN-3 signal has been sufficiently quenched. These observations have led to the hypothesis that the level of active MPK-1 and the amount of LIN-12-mediated signaling together determine 1° and 2° fates, respectively. Cells with high MPK-1 activity and low lateral activity commit to a 1° fate, and cells with low MPK-1 activity and high lateral activity commit to a 2° fate. Finally, cells lacking both MPK-1 and lateral activity acquire the 3° fate.

Based on this paradigm for fate specification, we examined the role of lateral coupling in segregating VPCs on a “fate plane,” where MPK-1 activity is represented on the ordinate and LIN-12 activity is represented on the abscissa (Fig. 6). Furthermore, our analysis was expanded to a linear array of six cells, topologically representative of the P3.p-P8.p VPCs (Fig. 1). The simulations were conducted with a gradient in inductive signal that decays as the square of the distance from the AC, characteristic of morphogen diffusion. The maximal inductive signal (I_P6.p) was applied to the P6.p cell, the VPC most proximal to the AC. Results for one side of the gradient (P3.p-P6.p cells) are presented because the response of P7.p and P8.p cells is nearly equivalent to that of P5.p and P4.p cells, respectively (Fig. 8, which is published as supporting information on the PNAS web site).

Fig. 6.

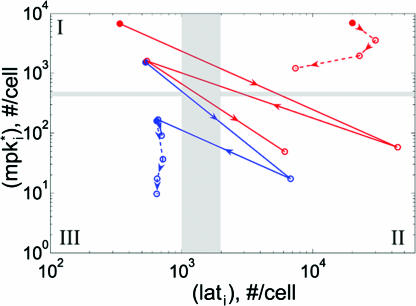
Wild-type and mutant alternating phenotypes on the fate plane. The position of P3.p-P6.p VPCs is depicted on a fate plane defined by two fate-determining signals, the intracellular product of inductive signaling (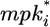, y axis) and the lateral signal (lat_i, x axis). The wild-type cell array (blue) was coupled (χ/χ° = 100) with μ = μ° and stimulated with two levels of inductive signal: I_P6.p = 10^-3 (dashed) or 10^-2 (solid). The mutant cell array (red) with hyperactive inductive signaling (μ = 10 μ°) was stimulated with I_P6.p = 10^-2 and was either uncoupled (χ/χ° = 0, dashed) or coupled (χ/χ° = 100, solid). The filled circle denotes the P6.p cell, and the empty circles mark the remainder of the cells (P5.p, P4.p, and P3.p) in the order indicated by the arrowheads. The three quadrants (I, II, and III) demarcated by the gray bars denote 1°, 2°, and 3° fates, respectively. The cells in the unmarked quadrant will adopt either 1° or 2° fate, but it cannot be determined which fate.

Our analysis shows that fate specification of the VPC array requires the inductive signal provided by the AC. At low morphogen levels (I_P6.p = 10^-3), there is no segregation of cells along the lateral signaling axis, suggesting that 2° fate specification depends on the level of inductive signal (Fig. 6). These results are consistent with the experimental observation that 2° fates are not observed in systems where the AC is laser-ablated (1). Thus, the response to low morphogen levels was used to parameterize the threshold amount of MPK-1^* (≈5 × 10² per cell) and lateral signal (≈10³ per cell) needed for 1° and 2° fates, respectively. Therefore, cells in quadrants I, II, and III are designated as 1°, 2°, and 3°, respectively (Fig. 6). Based on this parameterization of the fate plane, segregation of VPC fates is observed at higher inductive signals (I_P6.p = 10^-2) (Fig. 6). This result is in agreement with LIN-3 dosage experiments, wherein increasing LIN-3 production by the AC permits specification of 1° and 2° fates (4).

To further validate our model, we considered the striking phenotype observed among mutant animals with hyperactive LIN-3 signaling. In these mutant worms, VPCs acquire only 1° and 2° fates with a final pattern that precludes two adjoining 1° cells (20). Thus, a common phenotype among these mutants is the alternating fate pattern 1° 2° 1° 2° 1° 2°, a sharp contrast to the wild-type 3° 3° 2° 1° 2° 3° fate pattern. This alternating pattern has been reported in mutant animals with either lin-15(lf) or let-60(gf) mutations (6, 19, 21). The detailed molecular mechanism by which lin-15(lf) hyperactivates LIN-3 signaling remains unclear. In contrast, it is well established that let-60 encodes a Ras homolog that lies upstream of MPK-1 activation (22). Thus, we simulate the let-60(gf) mutation in our model by increasing the value of μ from its wild-type, reference value μ°.

As shown in Fig. 6, the mutant cell array (μ = 10 μ°) displays an alternating 1°-2° phenotype. The cells switch between a high MPK-1^*/low lateral state (P8.p, P6.p, and P4.p) and a low MPK-1^*/high lateral state (P7.p, P5.p, and P3.p) in the fate plane. Notably, a mutant cell array lacking any coupling (χ = 0) does not yield an alternating phenotype. Rather, all cells reside in the high MPK-1^*/high lateral signal state. Thus, our model accurately predicts the 1° 2° 1° 2° 1° 2° phenotype as observed experimentally in let-60(gf) mutants. Furthermore, our model demonstrates that lateral coupling is an essential mechanism to achieve this alternating phenotype.

Enhanced Segregation on the Fate Plane. Even in the absence of coupling (χ = 0), it is possible to distinguish cells based on their position along the lateral signaling axis (Fig. 7A; see also Fig. 9, which is published as supporting information on the PNAS web site). The P5.p cell acquires the highest lateral signal, because of its position next to the P6.p, the cell with greatest MPK-1 activity. These results suggest that the inductive signal-mediated bias of lateral signaling (Fig. 2, arrows marked k_x2 and k_x3) is sufficient to establish some degree of segregation of precursor cells on the fate plane.

Fig. 7.

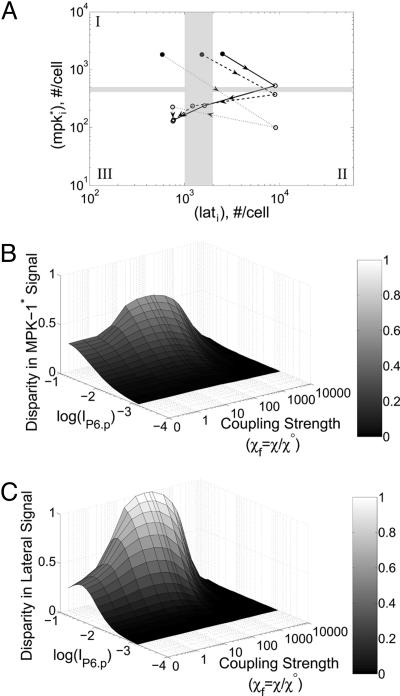
The effect of coupling on segregating two fate-determining signals in a six-cell array. (A) The position of P3.p-P6.p VPCs is depicted on the fate plane. The cell array was simulated with I_P6.p = 10^-2. The filled circle denotes the P6.p cell, and the empty circles mark the remainder of the cells (P5.p, P4.p, and P3.p) in the order indicated by the arrowheads. The lateral coupling strength was varied as χ_f = χ/χ° = 0 (solid), 1 (dashed), and 10 (dotted). (B and C) The disparity in MPK-1^* (B) and lateral signals (C) between the presumptive 1° and 2° cells was quantified for a wide range of inductive signal and coupling strengths. The disparity in MPK-1^* signal is the value of m_P5.p subtracted from the value of m_P6.p. For the disparity in lateral signal, a similar calculation was performed with the difference now computed in the value of lat.

Importantly, for coupled systems (χ > 0), the extent of fate segregation is amplified (Figs. 7A and 9). Increasing the value of χ reduces the lateral signal in both the P6.p and P4.p cells; concomitantly, an increase in coupling strength reduces the MPK-1 activity in the P5.p cell. Suppressing the lateral signal and MPK-1 activity in P6.p and P5.p cells, respectively, polarizes these cells destined to become 1° and 2° cells, respectively.

To gauge more quantitatively the dependence of fate segregation on coupling strength, we calculated the disparity in MPK-1^* and lateral signal activity between P6.p (presumptive 1°) and P5.p (presumptive 2°) cells for a wide range of inductive signal (I_P6.p) and coupling strength (χ) (Fig. 7 B and C). As noted earlier, establishing differences in MPK-1^* and lateral signal between P6.p and P5.p requires inductive signal. For low inductive signals (I_P6.p < approximately 10^-3), fate specification is not observed. Notably, for low to moderate coupling, an increase in coupling strength increases the segregation of the presumptive 1° and 2° cells with respect to both the MPK-1 signal and lateral signal (Fig. 7 B and C, respectively). However, at extremely high values of χ, even the basal level of constitutive lateral signaling suppresses MPK-1 activity. Because the perception of inductive signal is required for fate specification, extremely high coupling ablates fate specification entirely. Thus, our model predicts that moderate coupling enhances the segregation of fates determined by two signals, one involving a soluble inductive factor LIN-3 and the other transmitted by lateral cell-cell interactions via Notch-Delta signaling.

Model Development

VPCs are treated as a discrete, linear array of cells, wherein each cell, i, is stimulated by an inductive signal (Ind_i) corresponding to the number of LIN-3:LET-23 complexes per cell. The vector of inductive signals (Ind ={Ind_i}) defines the external morphogen gradient to which the VPC array responds. In each cell, the inductive signal (Ind_i) activates the MPK-1, producing MPK-1^* (Fig. 2). In turn, these active species are returned to their inactive state by the constitutive action of phosphatases.

In addition to constitutive deactivation, the level of MPK-1^* in each cell is affected by lateral signal activity. Lateral signal activity in cell i (lat_i) is received via the receptor LIN-12 and stimulates transcription of negative regulators of MPK-1. All together, the cumulative effects of inductive stimulation, constitutive deactivation and lateral signal-mediated deactivation determine the level of MPK-1^* as represented by the following differential equation:

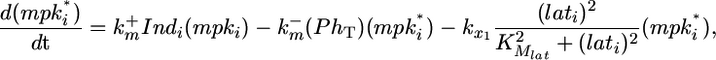[5]

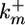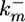where Ph_T is the amount of phosphatase per cell; and are the second-order rate constants for MPK-1 activation and constitutive deactivation, respectively; k_x1 is a rate constant for lateral signal-mediated deactivation of MPK-1^*. K_Mlat represents the width of the Hill function describing the transcriptional events associated with expression of MPK-1^* deactivators.

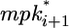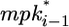The amount of lateral signal received by cell i (lat_i) is determined by two MPK-1-dependent processes. First, MPK-1^* stimulates the endocytic degradation of the LIN-12 receptor, thereby decreasing the reception of lateral signal. Second, active MPK-1 in neighboring cells ( and ) stimulates the synthesis of ligands for LIN-12, thereby increasing the lateral signal into cell i. In addition to these MPK-1^*-mediated effects, the level of lateral signal (lat_i) is determined by constitutive synthesis and degradation.

Because little quantitative information is available on the regulation of LIN-12 endocytosis and LIN-12 binding to its ligands within the intercellular space, we sought to capture the salient features of LIN-12 regulation. Thus, the model tracks the level of LIN-12 complexes with its ligands as a lumped measure of lateral signaling as follows:

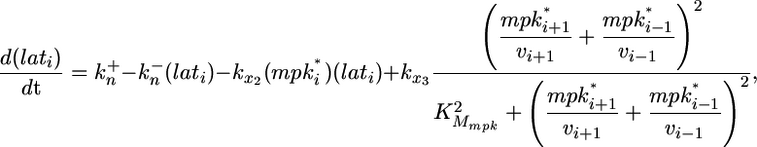[6]

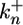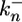where and are the constitutive rate constants of lateral signal generation and degradation, k_x2 is the rate constant for MPK-1^*-mediated down-regulation of lateral signaling by enhanced endocytosis of LIN-12, k_x3 is the rate constant for lateral signal transmission into cell i by its neighbors, and K_Mmpk represents the width of the Hill function describing the generation of lateral signal by MPK-1^*; υ_i-1 and υ_i+1 are the number of neighbors for cell i - 1 and i + 1, respectively. For a linear array, the value of υ_i is either 1 or 2. In Eqs. 5 and 6, we have assumed that transcriptional regulation occurs in a cooperative manner with a Hill coefficient (η_H) of 2; however, eliminating this cooperativity (η_H = 1) does not affect the trends predicted by the model.

It is meaningful to introduce the following substitutions:

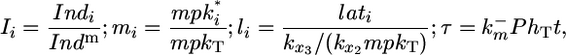[7]

where Ind^m is the maximum number of morphogen:morphogen-receptor complexes per cell, mpk_T is the total number of MPK-1 molecules per cell, and t is dimensional time. Incorporating these substitutions in Eqs. 5 and 6 yields the following differential equations:

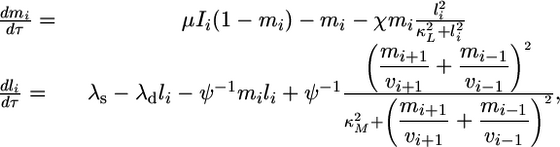[8]

where the dimensionless parameters μ, χ, K_Mlat, K_Mmpk, λ_s, λ_d, and Ψ are defined as follows.

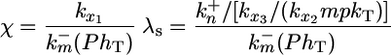Two dimensionless groups of particular importance are χ and Ψ, which together offer a gauge of intercellular coupling. The first parameter χ is a ratio of the time scale for constitutive deactivation of MPK-1^* to the time scale of lateral signal-mediated deactivation of MPK-1^*. Large values for χ indicate that constitutive deactivation of MPK-1^* occurs much slower than lateral signal-mediated deactivation. For example, a value of χ = 10 indicates that when lateral signaling is maximal, lateral signal-mediated deactivation of MPK-1^* occurs at a rate that is 10-fold greater than rate of deactivation mediated by constitutive pathways. The second parameter Ψ is a ratio of the time scale of MPK-1^*-mediated down-regulation of lateral signal to the time scale of MPK-1^* deactivation by phosphatases. Thus, large values for Ψ imply that a given MPK-1^* molecule is more likely to be deactivated before contributing to the down-regulation of lateral signal. Thus, large Ψ indicates that each cell is more susceptible to lateral effects. Reference values for these and other dimensionless parameters were chosen as outlined in Supporting Text and Tables 1 and 2, which are published as supporting information on the PNAS web site.

The outlined mathematical model differs significantly from a recent treatment of this system that used a statecharts approach (23), wherein the fate of a particular VPC is decided based on the state of its neighbors using fate decision rules. These rules are high-level abstractions of the underlying logic guiding fate determination as outlined in 1989 (19). Since then, significant advances have been made in our understanding of the intracellular signals occurring in each VPC and the molecular mechanisms by which VPCs are coupled. Our mathematical model encodes explicitly these intracellular molecular mechanisms and the coupling between VPCs, allowing a direct examination of the importance of these molecular interactions for spatial patterning of fates during C. elegans vulval development.

The analysis presented in this work focuses on the steady-state behavior of the model. Experiments wherein the AC is ablated at different times during the fate specification process have revealed that fate specification is unaffected if the AC is eliminated after a 5-h window (24, 25). Analysis of model dynamics shows that the time scale for reaching steady state is less than 5 h for reference values of parameters (data not shown). Thus, we proceed under the reasonable assumption that the steady state achieved during this time frame dictates fate specification.