TABLE 1.
Analysis of residues with significant exchange broadening
| Residue* | ΔRex* (s−1) | ΔΔRex†(s−1) | Rex* (s−1) |
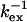 (μs)* (μs)*
|
 (ppm)* (ppm)*
|
f† |
|---|---|---|---|---|---|---|
| 14 | <0.7 | −2.3 | 4.5 | <33 | 1.5 | <0.5 |
| 19 | 3.4 | −3.6 | 12.0 | 55 | 2.8 | 0.6 |
| 27 | 1.6 | 0.0 | 8.6 | 40 | 2.8 | 0.8 |
| 28 | 2.0 | 1.1 | 7.2 | 55 | 2.2 | 0.9 |
| 36 | 2.2 | 1.6 | 1 | >220 | <0.8 | – |
| 39 | 4.7 | 1.5 | 23.8 | 40 | 4.6 | 0.9 |
| 42 | 4.2 | −1.0 | 1.7 | >210 | <0.9 | – |
| 51 | 0.5 | −1.5 | 2.8 | 37 | 1.2 | 0.5 |
| 55 | 6.2 | −7.8 | 28.0 | 45 | 4.6 | 0.6 |
| 57 | 2.9 | 1.45 | 1 | >230 | <0.8 | – |
| 60 | 3.3 | −0.1 | 5.8 | 90 | 1.7 | 0.8 |
| 72 | 2.3 | −0.0 | 10.0 | 20 | 2.8 | 0.8 |
| 73 | 2.2 | 0.4 | 7.9 | 62 | 2.3 | 0.9 |
| 75 | 1.6 | −0.3 | 6.5 | 50 | 2.2 | 0.8 |
| 76 | 0.6 | −8.9 | 11.0 | 15 | 5.0 | 0.4 |
| 77 | 1.9 | 0.7 | 8.5 | 45 | 2.6 | 0.8 |
| 92 | 2.2 | −1.1 | 8.3 | 55 | 2.4 | 0.7 |
| 112 | 3.4 | 1.7 | 8.0 | 70 | 2.2 | 0.9 |
| 113 | 3.2 | 1.2 | 9.5 | 60 | 2.4 | 0.9 |
| 115 | 4.6 | 1.2 | 1 | >300 | <1.1 | – |
| 118 | <0.7 | −2.0 | 3.3 | <35 | 1.4 | <0.5 |
| 142 | – | – | 20.3 | – | – | – |
| 144 | 0.8 | 0.5 | 8.0 | 20 | 3.6 | 0.8 |
| 146 | 5.8 | –0.7 | 9.9 | 90 | 2.2 | 0.8 |
| 147 | 2.7 | 1.7 | 2.2 | 145 | 1 | 0.9 |
Selected residues (selection value underlined) with either Rex > 6.4 s−1 or ΔRex > 2.5 s−1 or ΔΔRex < −1.4 s−1. The fast exchange equations were used to derive  from the correlation of ΔRex and Rex as explained in the Theory section. The error in
from the correlation of ΔRex and Rex as explained in the Theory section. The error in 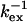 is estimated to be ∼30 μs and ∼1 ppm in
is estimated to be ∼30 μs and ∼1 ppm in 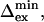 based on 1 s−1 errors in ΔRex and Rex;
based on 1 s−1 errors in ΔRex and Rex;  is calculated from
is calculated from 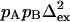 with pA = pB = 0.5 and represents the minimum value of Δex, because pApB reaches a maximum at pA = 0.5. The ΔRex showed a systematic offset of ∼−2 s−1. The values given and used in the derivation of
with pA = pB = 0.5 and represents the minimum value of Δex, because pApB reaches a maximum at pA = 0.5. The ΔRex showed a systematic offset of ∼−2 s−1. The values given and used in the derivation of 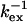 and
and  have been corrected for this offset. Residues 36, 42, 57, and 115 have small Rex; the
have been corrected for this offset. Residues 36, 42, 57, and 115 have small Rex; the  is a lower limit and the
is a lower limit and the 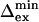 an upper limit based on a maximum value of Rex of 1 s−1.
an upper limit based on a maximum value of Rex of 1 s−1.
Residues 14, 19, 51, 55, 76, 92, 118, and 146 show a relatively high decrease in ΔRex (ΔΔRex < −0.5, italic) upon decrease in temperature, leading to relatively large fractional decrease in the exchange rate kex (f = kex,300/kex,308, italic; see Theory section for the equations used). Based on the error in ΔΔRex (1.4 s−1) and ΔRex (0.7 s−1), the error in f is estimated to be 0.15. For the four residues 36, 42, 57, and 115, no reliable estimate of f can be made, because of the uncertainty in the value of kex. For residues 14 and 118 the upper limit of f and  is given as estimated from the lower limit of ΔRex.
is given as estimated from the lower limit of ΔRex.
