Amino Acid Substitutions in the Pore of the Ca_V1.2 Calcium Channel Reduce Barium Currents without Affecting Calcium Currents

Abstract

Ba²⁺ currents through Ca_V1.2 Ca²⁺ channels are typically twice as large as Ca²⁺ currents. Replacing Phe-1144 in the pore-loop of domain III with glycine and lysine, and Tyr-1152 with lysine, reduces whole-cell G_Ba/G_Ca from 2.2 (wild-type) to 0.95, 1.21, and 0.90, respectively. Whole-cell and single-channel measurements indicate that reductions in G_Ba/G_Ca result specifically from a decrease in Ba²⁺ conductance and not changes in V_h or P_O. Half-maximal block of I_Li is increased by 3.2-, 3.8-, and 1.6-fold in Ca²⁺, and 3.8-, 4.2-, and 1.8-fold in Ba²⁺ for F1144G, Y1152K, and F1144K, respectively. High affinity interactions of individual divalent cations to the pore are not important for determining G_Ba/G_Ca, because the fold increases in IC₅₀ values for Ba²⁺ and Ca²⁺ are similar. On the contrary, conductance-concentration curves indicate that G_Ba/G_Ca is reduced because the interactions of multiple Ba²⁺ ions in the mutant pores are altered. The complexity of these interactions is exemplified by the anomalous mole fraction effect, which is flattened for F1144G and FY/GK but accentuated for F1144K. In summary, the physicochemical properties of the amino acid residues at positions 1144 and 1152 are crucial to the pore's ability to distinguish between multiple Ba²⁺ ions and Ca²⁺ ions.

INTRODUCTION

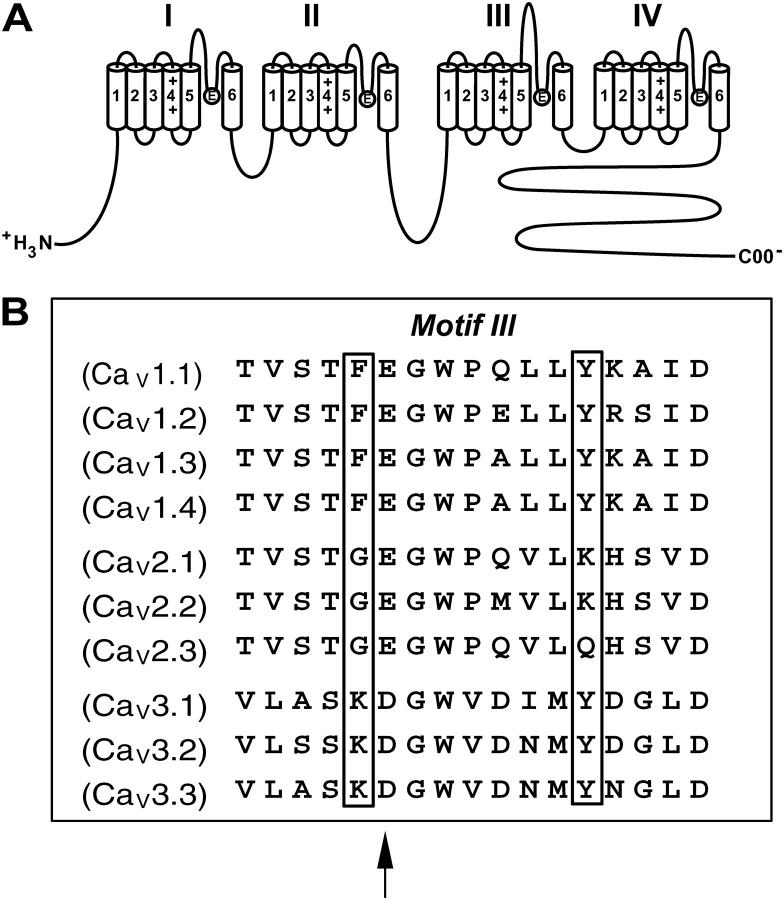
Voltage-gated Ca²⁺ channels are important for the regulation of Ca²⁺ homeostasis, neurotransmitter release, muscle contraction, and gene expression. Voltage-activated Ca²⁺ channels are heteromultimeric complexes consisting of α₁, β, α₂/δ, and sometimes γ-subunits. The pore-forming α₁ subunit contains all of the structural determinants required for voltage-dependent gating, drug binding, and ion permeation (Fig. 1 A). The membrane topology of the α₁ subunit consists of four homologous domains (I, II, III, IV), each consisting of six transmembrane segments (S1–S6). The connecting segments between S5 and S6 of each domain contain negatively charged glutamate residues that line the pore of the channel and form a binding site for Ca²⁺ ions called the selectivity filter (1).

FIGURE 1.

Phe-1144 and Tyr-1152 reside in the pore segment of domain III. (A) Transmembrane folding model of the α₁ subunit of high voltage-gated Ca²⁺ channels. The α₁ subunit consists of four homologous domains, each consisting of six transmembrane segments (S1–S6). Four glutamate residues, one residing in each of the four loops connecting S5 and S6 in each domain, form the selectivity filter, or EEEE locus. The selectivity filter is thought to bind a single divalent cation with a high affinity or multiple divalent cations with a low affinity. (B) Alignment of the domain III pore segment from each of the 10 Ca²⁺ channel family members. All high voltage-activated Ca²⁺ channels have a glutamate residue at position 1145, and all low voltage-activated Ca²⁺ channels have an aspartate residue at this position (arrow). All L-type Ca²⁺ channels (Ca_V1.1–4) have a phenylalanine, all high voltage-activated non-L-type Ca²⁺ channels (Ca_V2.1–3) have a glycine, and all low voltage-activated T-type Ca²⁺ channels (Ca_V3.1–3) have a lysine residue at position 1144 (boxed). All L-type Ca²⁺ channels (Ca_V1.1–4) and T-type Ca²⁺ channels (Ca_V3.1–3) have a tyrosine residue at position 1152, whereas two of three non-L-type Ca²⁺ channels (Ca_V2.1–2) have a lysine residue at this position.

There are two fundamental properties that are essential for the function of voltage-gated Ca²⁺ channels: permeation and gating. Ion permeation through the pore of a Ca²⁺ channel is complex because the channel must be highly selective for Ca²⁺ ions, while maintaining an extremely rapid flux rate. The crystal structure of the bacterial K⁺ channel, KcsA, has yielded valuable information about how K⁺ channels selectively transport K⁺ ions across the cell membrane (2–5), but the results of these studies shed little light on Ca²⁺ channel permeation for two main reasons: first, although the pores of Ca²⁺ and K⁺ channels are likely to share gross structural features, their respective selectivity filters are undoubtedly distinct at the atomic level. Importantly, the K⁺ channel pore is small, whereas the pore of the Ca²⁺ channel is very large (5,6) and selects Ca²⁺ ions over much more abundant ions such as Na⁺ by binding Ca²⁺ ions with a high affinity. Second, the main chain carbonyl oxygen atoms project toward the lumen of the K⁺ channel selectivity filter where they directly interact with K⁺ ions (5), whereas the side chains of four negatively charged glutamate residues in the Ca²⁺ channel selectivity filter project toward the lumen of the pore (7–10) and form a single binding site (the EEEE locus) capable of binding a single divalent cation with a high affinity or two divalent cations with a low affinity (11–19). Since, the mechanisms by which ions selectively pass through the pores of the two channels are fundamentally different, one cannot rely on the structural details of the KcsA pore to develop an understanding of ion permeation through the Ca²⁺ channel pore. The Ca²⁺ channel pore appears to resemble that of other ion channels such as the Na⁺ channels (19–22), so structural studies that reveal the molecular details of ion selectivity through Ca²⁺ channels are likely to have far-reaching applications to other classes of ion channels.

Ba²⁺ currents through L-type Ca²⁺ channels, as well as most other high voltage-activated Ca²⁺ channels, are approximately twice as large as Ca²⁺ currents (1,23,24). The differences between Ba²⁺ and Ca²⁺ conductance are thought to rely on the relative binding affinities single cations have for the selectivity filter (25–28). This phenomenon has been attributed to the observation that the binding affinity of a single Ba²⁺ ion to the selectivity filter is reported to be ∼70-fold lower than that of Ca²⁺ (29). The repulsive forces exerted by the entry of a second ion are thought to promote the exit of a Ba²⁺ ion more readily than it would a Ca²⁺ ion—this increased exit rate manifests itself as an increase in ionic flux. Although current theoretical models are dependent on the binding-repulsion events in the pore (25–28), it should be noted that Ca_V3 channels exhibit a higher affinity for Ca²⁺ than Ba²⁺ (30) even though the two ions have similar conductances. Thus, how Ba²⁺ and Ca²⁺ ions traverse the pore appears to be more complex than these models predict.

Current models for selectivity and permeation through voltage-gated Ca²⁺ channels would predict that neutralizing the glutamate residues in the EEEE locus would have a direct effect on the channel's maximum conductance and that the magnitude of this effect would be proportional to the magnitude of the effect on cation binding to the selectivity filter. This has not proven to be the trend. Neutralization of only the fourth domain glutamate, Glu-IV, results in a reduction in the conductance for Ba²⁺ ions (18,31). This is surprising because, of the four glutamate residues, neutralization of Glu-IV has the smallest effect on the high affinity binding of divalent cations to the selectivity filter (16). Thus, although the EEEE locus appears to form a high affinity binding site for divalent cations, additional amino acids help determine the selectivity and permeability properties of the Ca²⁺ channel, as well.

Very little work has been done to establish how amino acids proximal to the EEEE locus influence permeation and selectivity (32,33). We have identified mutant Ca²⁺ channels with nonglutamate substitutions in the pore that alter specific permeation properties of the channel (33,34). Most notably, the ratio of Ba²⁺ to Ca²⁺ currents at −10 mV (I_Ba(−10)/I_Ca(−10)) is substantially reduced for all four mutants. The large reductions in I_Ba(−10)/I_Ca(−10) result predominantly from a large reduction in G_Ba with little change in G_Ca. Measurements of half-maximal block of Li⁺ currents indicate that reductions in G_Ba/G_Ca do not result from changes in high affinity occupancy of single divalent cations in the pore. Instead, our findings indicate that the magnitude of G_Ba(max)/G_Ca(max) is dependent on complex interactions of multiple Ba²⁺ ions in the pore. The physicochemical properties of the amino acid residues at positions 1144 and 1152 are crucial to the pore's ability to distinguish between multiple Ba²⁺ ions and multiple Ca²⁺ ions.

EXPERIMENTAL PROCEDURES

Whole-cell patch-clamp recordings were acquired as described previously (35,36). Briefly, cDNAs encoding wild-type (37) and mutant Ca_V1.2 Ca²⁺ channels were cotransfected with β_2a (38), CaM₁₂₃₄ (35), and α₂δ (39) into HEK293 cells by calcium phosphate precipitation. CaM₁₂₃₄ encodes an inactive form of calmodulin. Overexpression of CaM₁₂₃₄ has been shown to eliminate Ca²⁺-dependent inactivation and facilitation of Ca_V1.2 channels (35,36,40,41). Therefore, CaM₁₂₃₄ was used in these experiments to eliminate complications that could arise from Ca²⁺/CaM-dependent changes in channel gating. All cDNAs were expressed in the expression plasmid, pCDNA3 (Invitrogen, Carlsbad, CA).

Whole-cell currents were recorded at room temperature 2–3 days after transfection. Briefly, pipettes (2.5–3.5 MΩ) were pulled from borosilicate glass using a Sutter (Novato, CA) P-97 Flaming/Brown micropipette puller and fire polished on a MF200 microforge (World Precision Instruments, Sarasota, FL). Four types of external solutions were used for whole-cell recordings: 1), The external solutions for measuring Ca²⁺ and Ba²⁺ currents in Figs. 2–6 contained (in mM): N-methyl-D-glutamine (NMG)-aspartate, 130; HEPES, 10; 4-aminopyridine, 10; glucose, 10; and CaCl₂ or BaCl²⁺, 10. The osmolarity was adjusted to 300 mmol/kg with sucrose and the pH was adjusted to 7.4. 2), The bath solutions for experiments where Ca²⁺- or Ba²⁺-dependent block of Li⁺ currents was assessed (Figs. 8 and 9) contained (in mM): LiCl, 100; HEPES, 10; TEA-Cl, 14; EDTA, 5; HE-EDTA, 5; and CaCl₂ or BaCl₂, as needed based on published binding constants (WINMAXC, Chris Patton, Stanford University). The pH of these solutions was adjusted using TEA-OH, and the osmolarity was adjusted to 300 mmol/kg using TEA-Cl. 3), External solutions similar to those used in No. 1 were used in experiments that assess conductance-concentration relationships (Fig. 10), except that glucose and NMG were added or removed as necessary to maintain the desired osmolarity of 300 mmol/kg. 4), External solutions for assessing the anomalous mole fraction effect (AMFE) (Fig. 11) were identical to external solution No. 1, except that combinations of Ca²⁺ and Ba²⁺ were used to give the desired molar ratio of the two ions and the total divalent cation concentration was held at 2.0 mM. The internal solution for all experiments contained (in mM) NMG-MeSO₃, 140; EGTA, 10; MgCl₂, 1; Mg-ATP, 4; and HEPES, 10.

FIGURE 2.

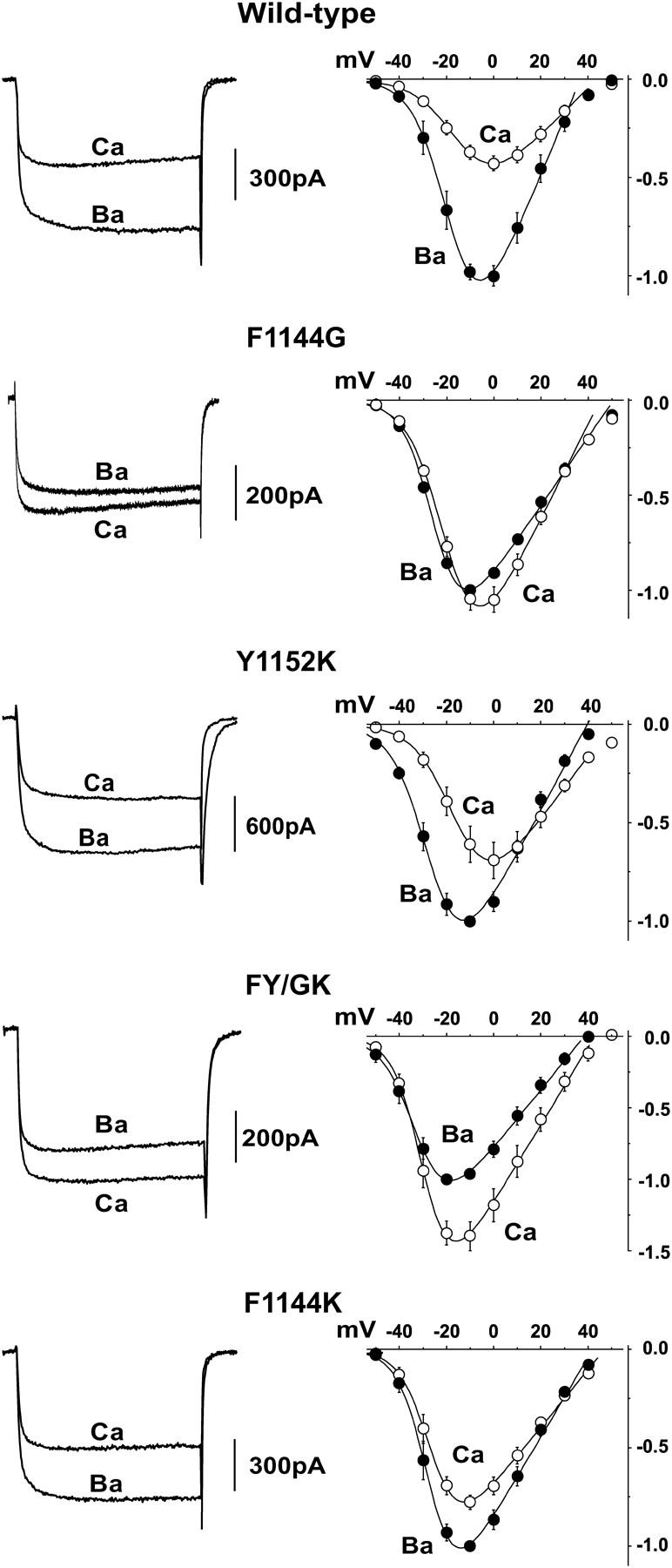
Alteration of nonglutamate residues in the pore segment of domain III reduces the channel's preference for passing Ba²⁺ currents over Ca²⁺ currents. (Left) Representative currents with 10 mM Ba²⁺ or 10 mM Ca²⁺ as the charge carrier. Currents were evoked by 150 ms step depolarizations to −10 mV from a holding potential of −90 mV. (Right) Current-voltage relations with Ba²⁺ (•) and Ca²⁺ (○) as the respective charge carriers are normalized to maximal Ba²⁺ currents recorded from the same cell and are plotted for comparison.

FIGURE 6.

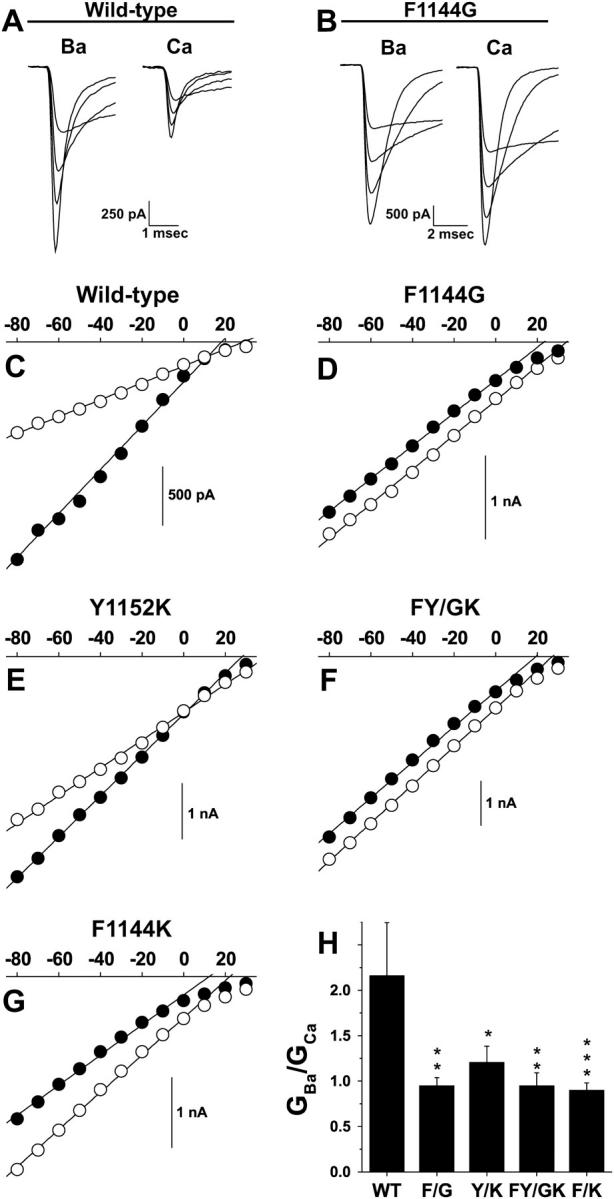
Whole-cell maximal slope conductances for F1144G, Y1152K, FY/GK, and F1144K are reduced. Whole-cell instantaneous I/V relations were generated by depolarizing wild-type and mutant cell membranes to +50 mV for 100 ms and then repolarizing them to test potentials ranging from −80 mV to +30 mV. (A and B) Tail currents evoked from repolarizing steps to −80, −60, −40, and −20 mV were generated in Ba²⁺ and Ca²⁺ from the same cell for wild-type (A) and F1144G (B). (C–G) Peak tail current amplitudes were measured in 10 mM Ba²⁺ (solid symbols) and 10 mM Ca²⁺ (open symbols) and plotted against the voltage of the repolarizing step. The linear portions of these data were fit using the equation I_tail = G × (V – E_rev), where I_tail is the peak tail current, G is the maximal slope conductance, and E_rev is the reversal potential. Reversal potentials extrapolated by linear fits are more negative than their true reversal potentials, because the open channel I–V is nonlinear near the reversal potential for calcium channels. H. G_Ba is divided by G_Ca from the same cell to give G_Ba/G_Ca. Notice G_Ba/G_Ca values exhibit the same trends as I_Ba(max)/I_Ca(max) values from Fig. 5: wild-type, 2.16 ± 0.58, n = 7; F1144G, 0.95 ± 0.087, n = 11; Y1152K, 1.21 ± 0.18, n = 8; FY/GK, 0.95 ± 0.14, n = 5; and F1144K, 0.90 ± 0.080, n = 9.

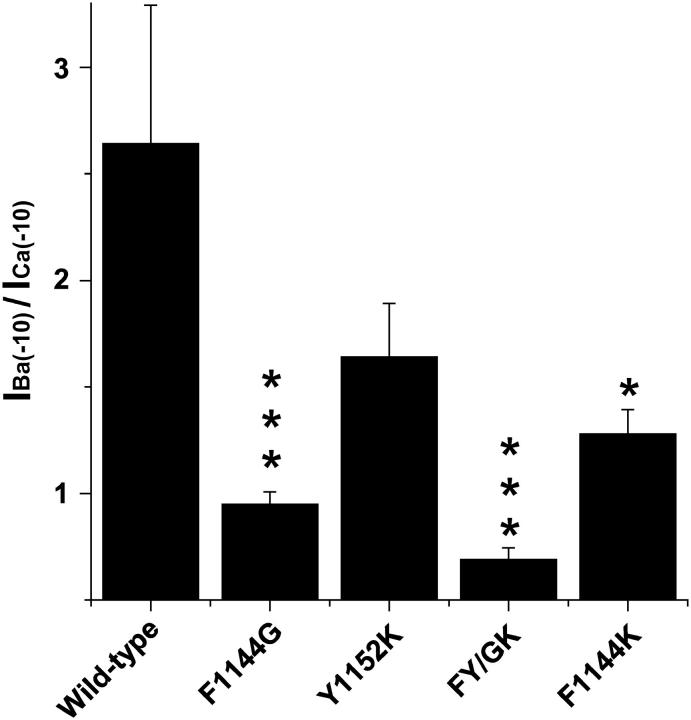
FIGURE 3.

Substitutions in the pore have large effects on I_Ba(−10)/I_Ca(−10). Quantitative analysis of data in Fig. 2. Ba²⁺ currents measured at −10 mV and were divided by Ca²⁺ currents measured at −10 mV to yield I_Ba(−10)/I_Ca(−10). Note that replacing Phe-1144 with glycine or lysine results in large decreases in I_Ba(−10)/I_Ca(−10), whereas modest effects are seen when Tyr-1152 is replaced by lysine. I_Ba(−10)/I_Ca(−10) values: wild-type, 2.64 ± 0.65, n = 6; F1144G, 0.95 ± 0.06, n = 8; Y1152K, 1.64 ± 0.25, n = 5; FY/GK, 0.69 ± 0.06, n = 5; and F1144K, 1.28 ± 0.06, n = 5.

FIGURE 4.

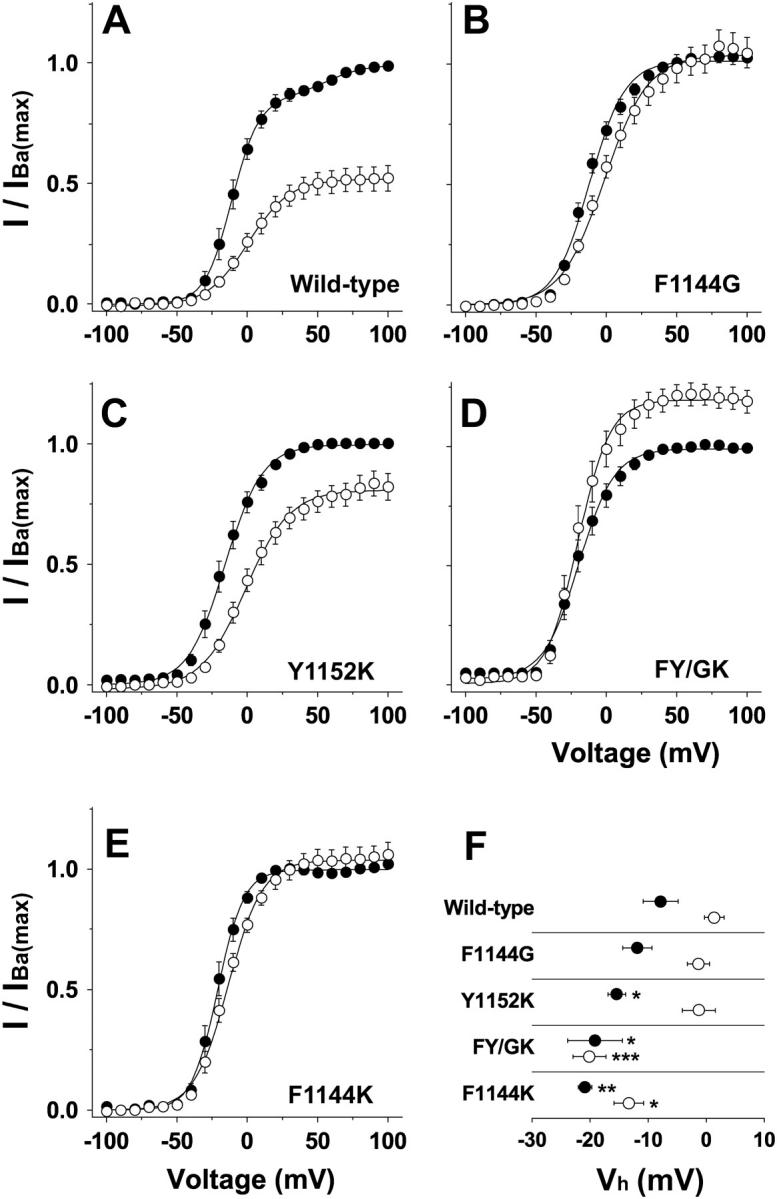
Substitutions in the pore segment of domain III produce small changes in the channel half-activation voltages. (A–E) Peak tail-currents were measured in Ba²⁺ (•) and Ca²⁺ (○) at −50 mV after 100 ms depolarizing potentials ranging from −100 to +100 mV. Smooth lines are single or double (wild-type, Ba²⁺) Boltzmann fits through data normalized to I_Ba(max). F. Mean V_h values derived from Boltzmann fits are plotted for wild-type and each mutant. V_h measured in Ba²⁺ (•): wild-type, −7.9 ± 3.1, n = 6; F1144G, −11.8 ± 2.1, n = 8; Y1152K, −15.4 ± 3.3, n = 5; FY/GK, −19.2 ± 3.5, n = 5; and F1144K, −20.9 ± 2.7, n = 5. V_h measured in Ca²⁺ (○): wild-type, +1.3 ± 2.5, n = 6; F1144G, −2.6 ± 1.7, n = 8; Y1152K, −1.8 ± 2.5, n = 5; FY/GK, −19.6 ± 3.0, n = 5; and F1144K, −14.2 ± 2.5, n = 5.

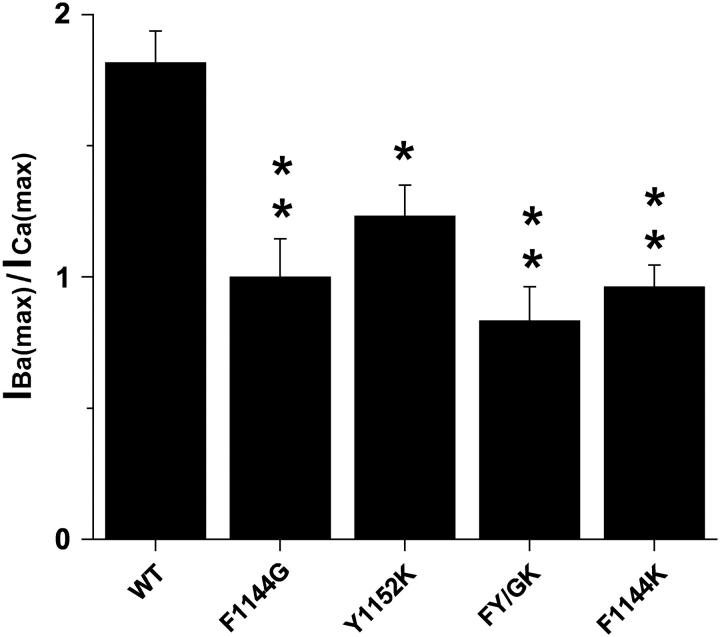
FIGURE 5.

Changes in V_h contribute to the observed changes in I_Ba(−10)/I_Ca(−10) for the mutant Ca²⁺ channels. Data in Fig. 4 were normalized to I_Ba(max). The relationship between I_Ba/I_Ba(max) and I_Ca/I_Ba(max) can be seen in Figs. 4 and 5. In Fig. 5, I_Ba(max)/I_Ca(max) is plotted as a bar graph so comparisons can be made with I_Ba(−10)/I_Ca(−10) from Fig. 3. I_Ba(max)/I_Ca(max) values: wild-type, 1.8 ± 0.12; F1144G, 1.0 ± 0.15; Y1152K, 1.23 ± 0.12; FY/GK, 0.83 ± 0.13; and F1144K, 0.96 ± 0.083.

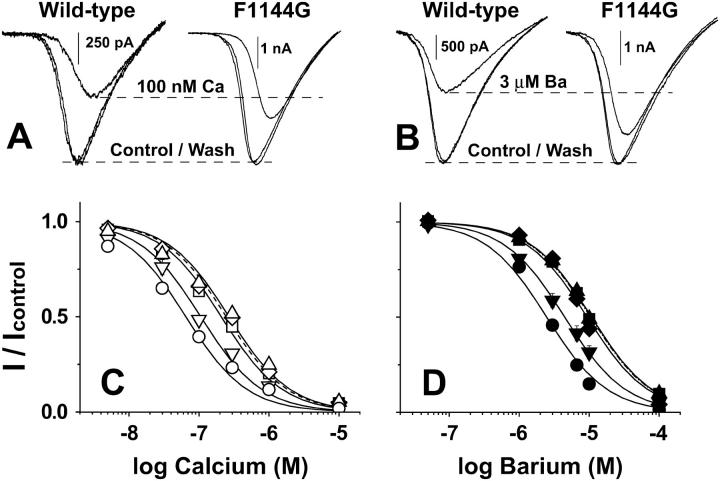
FIGURE 8.

High affinity binding of single Ba²⁺ and Ca²⁺ ions to the selectivity filters of F1144G, Y1152K, FY/GK, and F1144K is reduced. (A and B) Block of Li⁺ currents through wild-type (left) and F1144G (right) by 100 nM Ca²⁺ (A) and 3 μM Ba²⁺ (B). Currents were evoked using the ramping protocol described in Experimental Procedures. Peak currents measured at the indicated concentrations of free Ca²⁺ and Ba²⁺ were normalized to peak Li⁺ currents recorded at nominal free divalent concentrations. That control currents superimpose with currents measured at the end of each experiment (wash) demonstrates that rundown of Li⁺ currents was negligible. The small shifts in the I/V relations observed are likely due to ion-dependent effects on gating or voltage-dependent block. (C and D) Normalized Li⁺ currents were measured in the presence of the indicated concentrations of free external Ca²⁺ (C) and Ba²⁺ (D). IC₅₀ values determined in Ca²⁺ (nM): wild-type (•), 65 ± 7.6, n = 7; F1144G (▪) 208 ± 24, n = 4; Y1152K (♦), 246 ± 28, n = 4; FY/GK (▴), 269 ± 31, n = 5; and F1144K (▾), 106 ± 12, n = 4. Block of Li⁺ currents by Ba²⁺ (symbols and methods are the same as in A). IC₅₀ in μM: wild-type, 2.47 ± 0.17, n = 5; F1144G, 9.37 ± 0.64, n = 4; Y1152K, 10.5 ± 0.73, n = 5; FY/GK, 12.1 ± 0.90, n = 5; and F1144K, 4.49 ± 0.29, n = 4.

FIGURE 9.

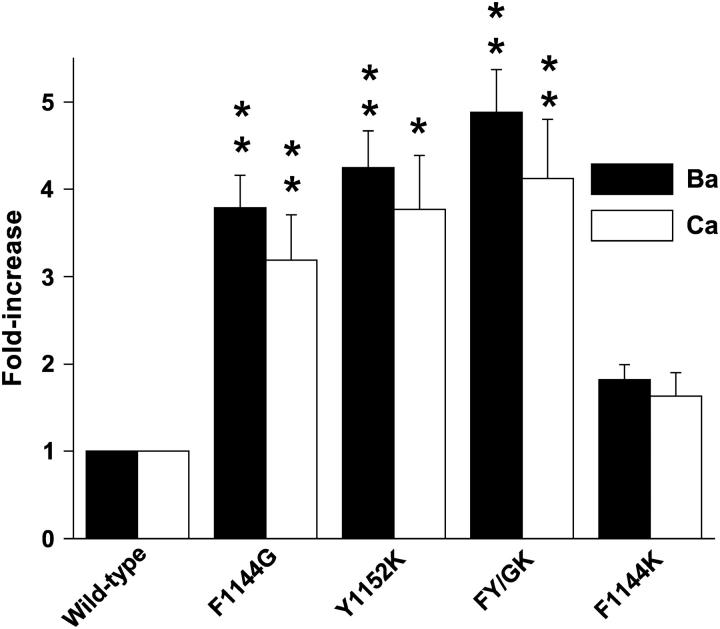
Differences in the binding affinities of individual Ba²⁺ and Ca²⁺ ions to the selectivity filter do not underlie the changes in G_Ba/G_Ca observed with the mutant channels. Fold increases in IC₅₀ values for half-maximal block of Li⁺ currents by Ba²⁺ (solid) and Ca²⁺ (open) are compared to wild-type. Note that mutant channels have reduced binding affinities for Ba²⁺ and Ca²⁺, but the fold decreases in the high affinity binding for Ba²⁺ and Ca²⁺ are approximately equal.

FIGURE 10.

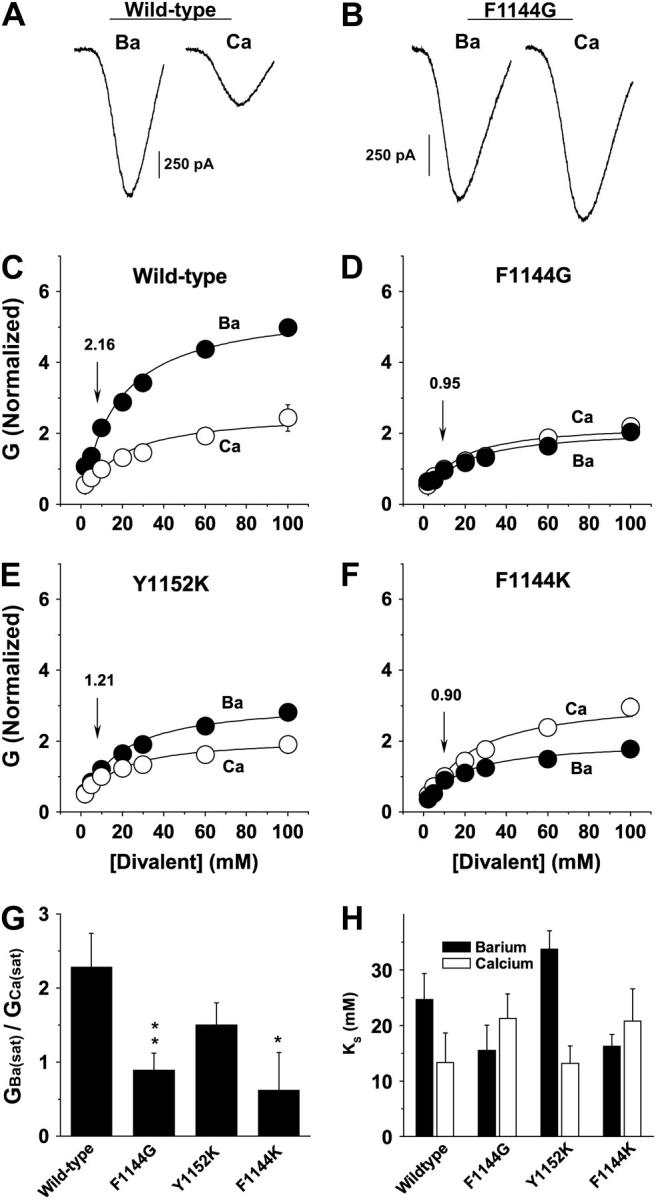
Relationship between saturating Ba²⁺ and Ca²⁺ conductance is altered for F1144G and F1144K. (A and B) Wild-type (A) and F1144G (B) currents with 100 mM Ba²⁺ (left) and 100 mM Ca²⁺ (right) as the respective charge carriers were evoked using the ramping protocol described in the Experimental Procedures. Notice that Ba²⁺ currents are more than twice the amplitude of Ca²⁺ currents for wild-type (A), whereas Ba²⁺ and Ca²⁺ currents through F1144G channels are about equal (B). (C–F) Maximal slope conductances were derived from fits through I/V relations measured at divalent concentrations ranging from 2 to 100 mM. Ba²⁺ (solid symbols) and Ca²⁺ (open symbols) were normalized by setting G_Ca measured in 10 mM Ca²⁺ to one and adjusting G_Ba measured in 10 mM Ba²⁺ to correspond with G_Ba/G_Ca determined in Fig. 6 H (numbers above arrows correspond to G_Ba/G_Ca in Fig. 6 H). This normalization procedure allows the direct comparison of the conductance-concentration curves at the whole-cell level with Ba²⁺ and Ca²⁺ as charge carriers. Maximal slope conductances were determined by Boltzmann fits using the equation, I = G × (V − E_rev)/(1 + exp((V − V_h)/K_S)), where G is the maximal slope conductance, E_rev is the reversal potential, V_h is the half-activating potential, and K_S is the slope. It is not yet possible to express the relationship between divalent cation concentration and conductance in mathematical terms because such equations are model dependent and the molecular details of ion permeation through voltage-gated Ca²⁺ channels are still controversial (11,28,57,58). However, the Michaelis-Menton equation is frequently used to estimate the apparent dissociation constant for low affinity binding of divalent cations to the pore and to approximate the saturating conductance (23,24,44,50,57,65,66). Therefore, data are fit using the Michaelis-Menton equation, G = G_sat/(1 + (K_S/c)), where G_sat is the level of current at saturating concentrations of divalent cations, c is the concentration of divalent cation, and K_S is the divalent cation concentration that produces one-half G_sat. G_Ba(sat): wild-type, 5.62 ± 0.34; F1144G, 2.13 ± 0.22; Y1152K, 3.12 ± 0.17; and F1144K, 1.99 ± 0.11. G_Ca(sat): wild-type, 2.46 ± 0.28; F1144G, 2.39 ± 0.23; Y1152K, 2.09 ± 0.12; and F1144K, 3.21 ± 0.30. For comparison with data in Figs. 5–7, data are plotted as G_Ba(sat)/G_Ca(sat) in panel G. (H) K_S values in mM are derived from Michaelis-Menton fits and plotted for Ba²⁺ (solid bars): wild-type 24.7 ± 4.6; F1144G 15.5 ± 4.5; F1144K 33.7 ± 3.3; and Y1152K 16.2 ± 2.1; and Ca²⁺ (open bars): wild-type, 13.3 ± 4.1; F1144G, 21.2 ± 6.8; F1144K, 13.2 ± 3.2; and Y1152K, 20.8 ± 5.7. Wild-type, n = 4; F1144G, n = 4; Y1152K, n = 4; and F1144K, n = 4.

FIGURE 11.

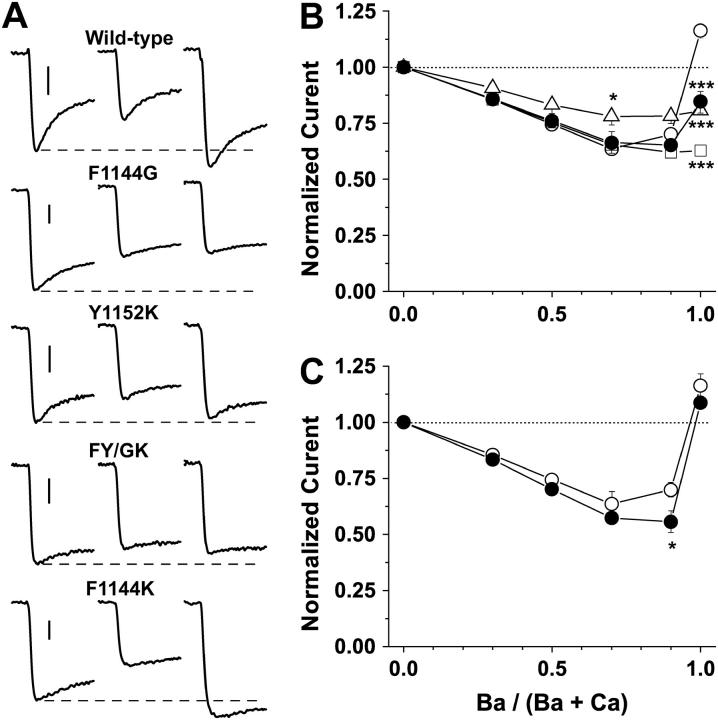
AMFE can be attenuated or accentuated by substitutions at Phe-1144. Cells were stepped from a holding potential of −90 to +50 mV for 100 ms, and peak tail currents evoked by stepping to −30 mV were measured at molar ratios of external Ba²⁺ to total divalent cation concentrations (Ba²⁺/(Ba²⁺ + Ca²⁺)) of 0.0, 0.3, 0.5, 0.7, 0.9, and 1.0. The combined divalent concentration (Ba²⁺ + Ca²⁺) at each data point was kept at 2 mM. (A) Sample peak tail currents for wild-type and mutant channels at Ba²⁺/(Ba²⁺ + Ca²⁺) ratios of 0 (left), 0.7 (center), and 1.0 (right). Dashed line corresponds to peak tail currents measured in an external solution containing 2.0 mM Ca²⁺ and 0.0 mM Ba²⁺. Scale bars, 200 pA. (B) AMFE is observed when peak tail currents, normalized to 1.0 when Ba²⁺/(Ba²⁺ + Ca²⁺) = 0, are plotted against Ba²⁺/(Ba²⁺ + Ca²⁺). Wild-type (○), F1144G (□), FY/GK (▵), and Y1152K (•). (C) AMFE for F1144K (•) is more pronounced than it is for wild-type (○). In B and C, identical results were obtained regardless of the order the divalent mixtures were added. Wild-type, n = 4; F1144G, n = 7; Y1152K, n = 5; FY/GK, n = 4; and F1144K, n = 5.

Data were acquired using a HEKA Epc9/2 amplifier and PULSE/PULSEFIT software. Currents were sampled at 10 kHz and low-pass filtered at 2 kHz. Series resistance was typically <6 MΩ and was compensated by ∼70%. Leaks and capacitive transients were subtracted using a P/4 protocol. A custom-made rapid-exchange gravity-flow single-barrel single-cell perfusion system with an internal barrel diameter of ∼0.2 mm was constructed that facilitated an exchange rate of <100 ms (data not shown). This apparatus was used in combination with a ramping protocol (−80 to +80 mV at a rate of 1 mV/ms) in Figs. 8 and 10. This approach greatly minimized complications resulting from current rundown, leak, and seal instability associated with Li⁺ currents: entire dose-response curves were typically completed in <5 min with a high degree of reproducibility and little or no rundown. This approach assumes that changes in peak current reflect changes in permeation and not gating. Most of the solutions used in these studies are balanced such that junction potentials in 10 mM Ba²⁺ and Ca²⁺ are negligible (0.04 and 0.16 mV, respectively). Rather than correcting for junction potential offsets during the course of an experiment, junction potential offsets were ignored for experiments in Fig. 8 (where the junction potentials ranged from +7.4 to +9.2 mV as the divalent concentrations were increased from 5 nM to 10 μM in Ba²⁺, and from +7.6 to +9.2 mV as the divalent concentrations were increased from 5 nM to 10 μM in Ca²⁺) and Fig. 10 (where the junction potentials ranged from −2 to +12 mV as the divalent concentrations increased from 2 to 100 mM). Since the peak currents measured in Figs. 8 and 10 were obtained using a ramping protocol, the magnitudes of junction potential offsets for wild-type and mutant channels were the same. Thus, junction potentials did not affect the comparisons made in these studies.

Single-channel recordings were obtained using the patch clamp technique in the cell-attached configuration (42). For single Ca²⁺ currents, the pipette solution contained 110 mM CaCl₂, 10 mM HEPES, pH 7.5 with TEA-OH. To record single channel Ba²⁺ currents, CaCl₂ was replaced with 110 mM BaCl₂. The bath solution contained 140 mM potassium aspartate, 10 mM EGTA, 10 mM HEPES, pH 7.5 with KOH. Five micromolar Bay K 8644 was included in both the pipette and bath solutions in all recordings. Bay K 8644 is routinely used to prolong opening of single L-type calcium channels to facilitate measurement of single-channel current amplitudes. Bay K 8644 has previously been shown not to affect single-channel conductance (43–45), but see (46–51). No noticeable differences in current amplitudes were noted between patches with and patches without Bay K 8644, although in the absence of Bay K 8644 it was admittedly difficult to identify openings of long enough duration to resolve to make these judgments. Recordings were performed at room temperature, using an Axopatch 200B integrating patch clamp amplifier and pCLAMP software. Single-channel currents were elicited by 300 ms long depolarizations to potentials ranging from −30 mV to +30 mV, from holding voltages of −70 mV to −90 mV. Recordings were filtered at 1 kHz and sampled at 10 kHz.

Data are mean ± SEM. Error bars smaller than symbols do not appear in figures. Propagated errors were determined using conventional statistical approaches (52): *p < 0.05; **p < 0.005; ***p < 0.0005.

RESULTS

Alteration of nonglutamate residues in the pore segment of domain III reduces the channel's preference for passing Ba²⁺ currents over Ca²⁺ currents

All of the mutagenic studies to date indicate that the glutamate residue in the pore of domain III is the most important determinant for ion permeation and selectivity (11–13,15–18). An alignment of the domain III pore segments from all 10 families of voltage-gated Ca²⁺ channels (Fig. 1 B) indicates that this segment is highly conserved. Note that all L-type Ca²⁺ channels (Ca_V1.1–4) possess a phenylalanine at position 1144, located immediately adjacent to Glu-1145 (arrow), whereas all non-L-type high voltage-activated Ca²⁺ channels (Ca_V2.1–3) possess a glycine and all low voltage-activated Ca²⁺ channels (Ca_V3.1–3) possess a lysine at this position. Tyr-1152 is located eight residues downstream of Phe-1144. All L- and T-type Ca²⁺ channels possess a tyrosine at this position, whereas non-L-type high voltage-activated Ca²⁺ channels have either a lysine or a glutamine at this position. That Phe-1144 and Tyr-1152 may be important for permeation and/or gating was first suggested by our findings that Phe-1144 (34) and Tyr-1152 (Blaise Z. Peterson, unpublished results) are important molecular determinants for Ca²⁺-dependent dihydropyridine (DHP) binding to L-type Ca²⁺ channels, whereas Gln-1149, positioned between Phe-1144 and Tyr-1152, is not important for Ca²⁺-dependent DHP binding (Blaise Z. Peterson, unpublished results). That DHP and Ca²⁺ binding is cooperative and DHPs modulate the gating (53) and perhaps conductance ((46–51), but see (43–45)) properties of L-type Ca²⁺ channels suggests that the gating and/or conductance properties of the channels is dependent on the identity of the residues that occupy positions 1144 and 1152.

To test this hypothesis, single mutants were made by substituting glycine and lysine into positions 1144 and 1152, respectively, to make Ca_V1.2 more Ca_V2.1-like and substituting lysine into position 1144 to make Ca_V1.2 more Ca_V3-like. To determine whether positions 1144 and 1152 act cooperatively to generate the Ca_V2.1-like phenotype, the double mutant FY/GK was constructed by simultaneously substituting glycine and lysine into positions 1144 and 1152, respectively. Since Phe-1144 and Tyr-1152 are both located in the Ca²⁺ channel pore, we first assessed the permeability properties of the mutant channels by comparing the relative amplitudes of Ba²⁺ and Ca²⁺ currents through each of the mutant channels with wild-type (Fig. 2). As is indicated in the upper panels of Fig. 2 and the summarized data in Fig. 3, Ba²⁺ currents at −10 mV through wild-type L-type Ca²⁺ channels were typically ∼2.6 times larger than Ca²⁺ currents measured at the same potential from the same cell. In contrast, the ratios of I_Ba(−10)/I_Ca(−10) for F1144G and FY/GK were decreased to only 0.95 and 0.69, respectively. The I_Ba(−10)/I_Ca(−10) values for Y1152K and F1144K were reduced to a lesser extent to 1.69 and 1.28, respectively. Therefore, nonglutamate substitutions in the pore segment of domain III are important for determining the channel's preference for passing Ba²⁺ ions over Ca²⁺ ions.

Small changes in voltage-dependent activation contribute to the observed changes in I_Ba(−10)/I_Ca(−10) for the mutant Ca²⁺ channels

The amplitude of whole-cell currents at −10 mV can be described using the following relation: I = n × P₍₋₁₀₎ × i₍₋₁₀₎, where n is the number of functional Ca²⁺ channels in the plasma membrane, P_o(−10) is the single-channel open probability at −10 mV, and i₍₋₁₀₎ is the single-channel current at −10 mV. Since I_Ba(−10)/I_Ca(−10) is determined from the same cell, the number of channels does not change. Therefore, it is only necessary to determine whether relative changes in P_o(−10) or i₍₋₁₀₎ contribute to the observed changes in I_Ba(−10)/I_Ca(−10) for the mutant channels.

The current-voltage relations of Fig. 2 (right) suggests that the estimated half activation voltage, V_h, may be altered for the mutant channels. The I/V relation for wild-type Ca²⁺ channels with Ca²⁺ as the charge carrier is typically shifted ∼10 mV to the right of the I/V measured with Ba²⁺ as the charge carrier, an effect often attributed to differences in the shielding effects between the two ions (1). For Y1152K, V_h measured in Ba²⁺ is shifted slightly to the left compared to wild-type, whereas the V_h measured in Ca²⁺ is indistinguishable from that of wild-type. Such an ion-specific shift in gating could alter I_Ba(−10)/I_Ca(−10) without changing the conductance of the channel for either ion. Likewise, I/V relationships measured with both Ba²⁺ and Ca²⁺ appear shifted to the left for FY/GK and F1144K.

Since changes in the voltage dependence of activation will directly affect P_o(−10), we used a quantitative approach to assess how amino acid substitutions at positions 1144 and 1152 specifically affect this property. In Fig. 4, tail currents were evoked at −50 mV after 100 ms voltage steps to the indicated potentials. Tail currents measured with Ba²⁺ and Ca²⁺ as the respective charge carriers were normalized to the largest tail currents elicited in Ba²⁺. These data, which reflect the voltage dependence of channel activation, show trends qualitatively similar to those observed with the I/V relations depicted in Fig. 2. For wild-type channels, V_h, the midpoint of the tail-current/voltage curve measured with Ba²⁺ and Ca²⁺ as the charge carrier is −7.9 and +1.3 mV, respectively. For F1144G and Y1152K, V_h determined in Ca²⁺ is indistinguishable from wild-type. In Ba²⁺, however, V_h for Y1152K is shifted 7 mV to the left. V_h determined with Ba²⁺ and Ca²⁺ as the charge carrier is shifted for FY/GK and F1144K: with Ca²⁺ as the charge carrier, V_h is shifted 21 and 16 mV in the hyperpolarizing direction, and V_h is shifted 11 and 13 mV in the hyperpolarizing direction when Ba²⁺ is the charge carrier for FY/GK and F1144K, respectively.

Although the negative shifts in V_h for Ba²⁺ and Ca²⁺ are about equal for F1144K, the changes in V_h observed for FY/GK and, to a lesser extent, Y1152K are asymmetrical. That is, V_h for FY/GK in Ca²⁺ is shifted 10 mV to the left more than V_h determined with Ba²⁺ as the charge carrier, and V_h for Y1152K in Ba²⁺ is shifted 4.4 mV to the left more than V_h determined when Ca²⁺ as the charge carrier. These ion-dependent changes in V_h suggest that ion binding in the pore can alter either the energetics of channel opening or local field potentials. That the phenotype of FY/GK does not simply reflect the sum of the effects on V_h for F1144G or Y1152K suggests that Phe-1144 and Tyr-1152 are codependent at determining the activation properties of the channel.

Although the effects on channel activation described above suggest that changes in I_Ba(−10)/I_Ca(−10) (Figs. 2 and 3) result at least partially from changes in the voltage dependence of channel activation (V_h), Fig. 4 demonstrates that alterations in I_Ba(−10)/I_Ca(−10) are dominated by factors other than V_h. In panels A–E, the I/I_Ba(max) curves for Ca²⁺ were normalized to I_max for Ba²⁺ (I_Ba(max)). Normalizing the data in this way provides a means to compare maximal Ba²⁺ and Ca²⁺ currents from the same cell at voltages where P_O is maximal (e.g., +100 mV). It is evident that I/I_Ba(max) for all four mutant channels differs substantially from that of wild-type. The bar plot in Fig. 5 provides a quantitative summary of the magnitudes to which I_Ba(max)/I_Ca(max) is decreased for F1144G, Y1152K, FY/GK, and F1144K. It is noteworthy that significant effects on conductance of Y1152K are masked by the Ba²⁺-specific shift in V_h depicted in Fig. 4 (compare Figs. 3 and 5).

Substitutions at positions 1144 and 1152 reduce channel Ba²⁺ conductance but have little effect on Ca²⁺ conductance

The I/I_Ba(max) measurements in Figs. 4 and 5 indicate that changes in V_h are responsible for only a small fraction of the changes in I_Ba(−10)/I_Ca(−10) for the mutant channels (Figs. 2 and 3). These experiments do not distinguish between changes in P_O and G, however, because at +100 mV where P_O is maximal, reductions in I_Ba(−10)/I_Ca(−10) can occur if P_O in Ca²⁺ is increased, P_O in Ba²⁺ is decreased, Ba²⁺ conductance is decreased, or Ca²⁺ conductance is increased. To assess the conductance properties of F1144G, Y1152K, FY/GK, and F1144K in isolation, the maximal slope conductance was determined for wild-type and mutant channels using whole-cell instantaneous I/V relations (Fig. 6) and single-channel recordings (Fig. 7).

FIGURE 7.

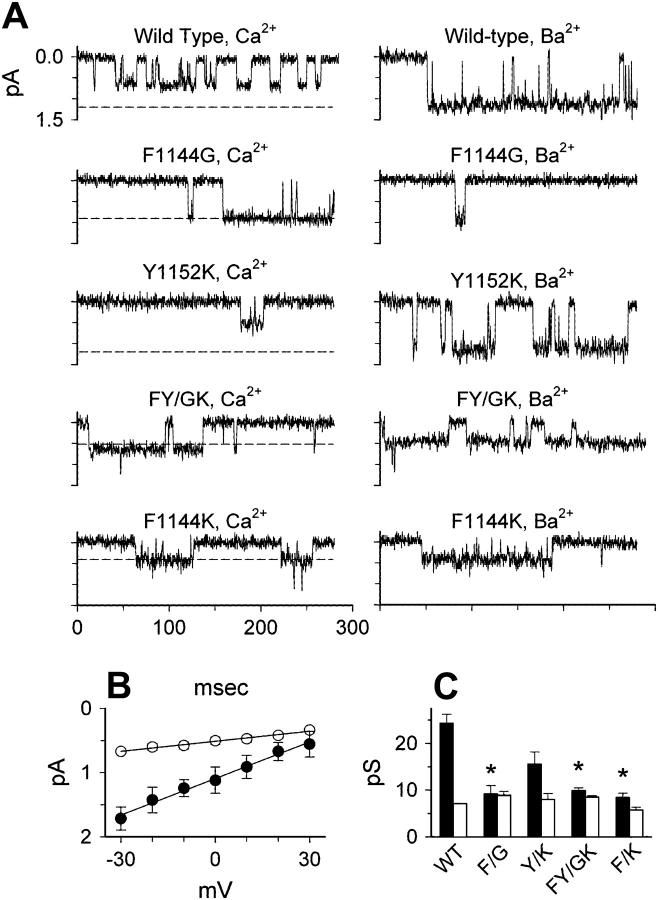
Mutants F1144G, F1144K, and FY/GK reduce single-channel Ba²⁺ currents but have little effect on single-channel Ca²⁺ currents. (A) Example traces, showing currents through single wild-type or mutant channels, with either 110 mM Ca²⁺ (left) or 110 mM Ba²⁺ (right) as the charge carrier. Currents were evoked by depolarizations to −10 mV. The dashed lines in the left-hand set of traces show the amplitudes of Ba²⁺ currents in the corresponding channel type, for comparison. (B) Mean current-voltage relationships for single wild-type channels, with Ca²⁺ (○) or Ba²⁺ (•). The straight lines are linear fits of the data points, with conductance values of 19.0 pS for Ba²⁺ and 7.1 pS for Ca²⁺. (C) Summary of single-channel conductance values for Ba²⁺ (solid bars) versus Ca²⁺ (open bars). Conductance values were determined from the following numbers of patches: wild-type, Ca²⁺, n = 4, Ba²⁺, n = 3; F1144G, Ca²⁺, 5, Ba²⁺, 4; Y1152K, Ca²⁺, 3, Ba²⁺, 4; FY/GK, Ca²⁺, 3, Ba²⁺, 3; F1144K, Ca²⁺, 4, Ba²⁺, 3.

As expected for wild-type, I_tail is substantially larger at each potential in Ba²⁺ compared to that measured in Ca²⁺ (Fig. 6 A). This trend is depicted graphically in Fig. 6 C. Note that I_tail for Ba²⁺ (solid circles) is substantially larger than I_tail for Ca²⁺ at all potentials in the linear range. Note also, that the slope of the linear fit (the maximal slope conductance) is steeper for Ba²⁺ than it is for Ca²⁺. The ratio of the maximal slope conductances in Ba²⁺ versus Ca²⁺ (G_Ba/G_Ca) for wild-type is 2.16 (Fig. 6 H), a value similar to the I_Ba(max)/I_Ca(max) of 1.8 determined for wild-type in Fig. 5. F1144G shows a different trend. Note in panels B and D in Fig. 6 that I_tail in Ba²⁺ is similar to that determined in Ca²⁺ and that the linear fits through the two sets of data (i.e., the maximal slope conductances) are similar. These data are represented quantitatively in Fig. 6 H where G_Ba/G_Ca for F1144G is equal to 0.95, a value substantially lower than that for wild-type. Similar analyses were performed on Y1152K, FY/GK, and F1144K (Fig. 6, E–G), resulting in G_Ba/G_Ca values for Y1152K, FY/GK, and F1144K of 1.21, 0.95, and 0.90, respectively (Fig. 6 H).

The data in Figs. 4–6 demonstrate that changes in I_Ba(−10)/I_Ca(−10) that result when Phe-1144 and Tyr-1152 are altered (Figs. 2 and 3) result primarily from changes in the channel's conductance properties and to a lesser extent V_h. By exclusion, P_O appears to play an insignificant role (note similarity between Figs. 5 and 6 H). It is not possible, however, to determine whether these substitutions reduce G_Ba/G_Ca by decreasing Ba²⁺ conductance or increasing Ca²⁺ conductance. To investigate how substitutions at positions 1144 and 1152 specifically affect the conductance of Ba²⁺ versus Ca²⁺, single-channel recordings of wild-type and mutant channels were measured using 110 mM Ba²⁺ or 110 mM Ca²⁺ as the charge carriers. Fig. 7 A shows example single-channel traces, elicited at a test potential of −10 mV. Consistent with previous results (44), single-channel currents carried by Ba²⁺ were approximately twice as large as currents carried by Ca²⁺. Mutation Y1152K had little effect on the relative amplitudes of Ca²⁺ versus Ba²⁺ currents; however, for mutants F1144G, F1144K, and FY/GK, Ba²⁺ currents were substantially reduced compared to wild-type. As a result, these mutant channels conducted Ca²⁺ and Ba²⁺ approximately equally well. To quantify this effect, we determined single-channel slope conductance values from linear fits of single-channel current amplitudes evoked at test potentials ranging from −30 mV to +30 mV (Fig. 7 B). These data are summarized in Fig. 7 C. As expected, for wild-type channels, Ba²⁺ conductance was 2.7 times larger than Ca²⁺ conductance (∼19 vs. ∼7.1 pS), whereas Ba²⁺ conductance values for F1144G, F1144K, and FY/GK were greatly reduced compared to wild-type and were approximately equal to Ca²⁺ conductance values. In addition to confirming our whole-cell data, these single-channel results demonstrate that mutations at position 1144 selectively reduce the maximal Ba²⁺ conductance of L-type Ca²⁺ channels while having little or no effect on maximal Ca²⁺ conductance. In the following sections, the mechanistic details that lead to these decreases in Ba²⁺ conductance are probed by measuring high and low affinity cation binding to the pore and the relationship between the two.

High affinity binding of single Ba²⁺ and Ca²⁺ ions to the selectivity filters of F1144G, Y1152K, FY/GK, and F1144K is reduced

Voltage-gated Ca²⁺ channels are highly selective for divalent cations (e.g., P_Ca/P_K > 1000; (1)) but become permeable to monovalent cations when divalent cations are removed from the bath. For example, large Li⁺ currents are observed when cells expressing voltage-gated Ca²⁺ channels are perfused in a divalent-free bath solution (1). The robustness of these monovalent currents has been attributed to the fact that monovalent cations are not sufficiently charged to bind tightly to the negatively charged selectivity filter. Therefore, the dwell time for each permeant monovalent cation is short, resulting in a rapid flux rate. Low concentrations of divalent cations block monovalent currents such as Li⁺ by interacting tightly with the selectivity filter and preventing the passage of Li⁺ ions through the single-file pore.

The IC₅₀ for half-maximal block of Li⁺ currents by Ca²⁺ (Fig. 8, A and C) and Ba²⁺ (Fig. 8, B and D) was used to approximate the dissociation constants for the binding of single Ca²⁺ and Ba²⁺ ions to the selectivity filters of wild-type and mutant channels. As expected, the apparent IC₅₀ for Ca²⁺ is 38-fold lower than that for Ba²⁺. Substituting Phe-1144 with glycine increases the IC₅₀ values for half-maximal block of Li⁺ currents by Ca²⁺ (open symbols) and Ba²⁺ (solid symbols) by 3.2- and 3.8-fold, respectively. A smaller effect is observed when Phe-1144 is replaced by lysine: the IC₅₀ for half-maximal block of Li⁺ currents by Ca²⁺ and Ba²⁺ are increased by 1.6- and 1.8-fold, respectively. The largest effect for the single amino acid substitutions is seen when Tyr-1152 is changed to lysine and half-maximal block is increased 3.8- and 4.2-fold in Ca²⁺ and Ba²⁺, respectively. Though not statistically significant, the IC₅₀ values that result from combining F1144G and Y1152K (FY/GK) were consistently greater than either single mutant alone (4.1-fold in Ca²⁺ and 4.9-fold in Ba²⁺).

The data in Fig. 8 are summarized in Fig. 9, where the IC₅₀ values determined for each mutant are divided by the IC₅₀ for wild-type to give the fold increases in Ba²⁺ (solid bars) and Ca²⁺ (open bars). Notice that the IC₅₀ for half-maximal block of Li⁺ currents by Ca²⁺ and Ba²⁺ is increased for F1144G, Y1152K, FY/GK, and F1144K, yet the fold increases in IC₅₀ values for Ba²⁺ and Ca²⁺ each ion are similar for each mutant—i.e., the changes in the high affinity binding of individual divalent cations to the pores of the mutant channels are not ion specific. Note also that high affinity binding of individual divalent cations to Y1152K is more severely altered than it is to the other mutants with single amino acid substitutions, yet G_Ba/G_Ca for Y1152K is the least affected of the mutants (Figs. 6 and 7). Thus, even though the residues at positions 1144 and 1152 are clearly important for determining the binding affinities of individual Ca²⁺ and Ba²⁺ ions to the selectivity filter, the changes we observe in the mutant channels' preferences for conducting Ba²⁺ over Ca²⁺ ions are not dependent on how single ions interact with the pore.

The relationship between saturating Ba²⁺ and Ca²⁺ currents is altered for F1144G and F1144K but not Y1152K

The data for F1144G, Y1152K, FY/GK, and F1144K in Figs. 8 and 9 indicate that the decreases in Ba²⁺ conductance does not result from changes in how individual Ba²⁺ ions interact with the pores of the mutant channels. Thus, it is likely that the substitutions have altered how multiple ions interact within the pores of the mutant channels. To test this, we compared the maximal slope conductances from currents generated in bath solutions containing Ba²⁺ or Ca²⁺ at concentrations ranging from 2 to 100 mM (Fig. 10). Notice in Fig. 10 A that the peak current is more than twice as large when 100 mM Ba²⁺ is the charge carrier than when 100 mM Ca²⁺ is the charge carrier. This is not the case for F1144G where peak currents in 100 mM Ba²⁺ and 100 mM Ca²⁺ are approximately equal (Fig. 10 B). In Fig. 10 C–F, the maximal slope conductances are determined for wild-type, F1144G, Y1152K, and F1144K at the indicated Ba²⁺ and Ca²⁺ concentrations and fit using the Michaelis-Menton equation. Saturating Ba²⁺ conductance through wild-type channels is ∼2.3-fold larger than saturating Ca²⁺ conductance (Fig. 10, C and G). Saturating Ba²⁺ conductance relative to Ca²⁺ conductance is greatly reduced for F1144G and F1144K, yielding G_Ba(sat)/G_Ca(sat) values of 0.89 and 0.51, respectively (Fig. 10, D, F, and G). Although G_Ba(sat)/G_Ca(sat) for Y1152K was consistently smaller than wild-type, this difference was not statistically significant (Fig. 10, E and G). The K_S values for F1144G, F1144K, and Y1152K are not significantly different from wild-type (Fig. 10 H).

These results are in agreement with those in Figs. 6–9, indicating that the identity of the residues at positions 1144 and 1152 determine the magnitude of G_Ba/G_Ca by specifically altering how multiple Ba²⁺ ions interact in the pore. Although the single-channel data (Fig. 7) demonstrate that G_Ba/G_Ca is reduced for each of the mutant channels because Ba²⁺ conductance is reduced, the experiments in Fig. 10 demonstrate that G_Ba decreases because G_Ba(sat) is decreased and not because K_S is increased.

The AMFE can be accentuated or attenuated by substituting Phe-1144 with glycine or lysine

The multi-ion nature of the Ca²⁺ channel pore has long been the subject of investigation. Hess and Tsien (26) and Almers and McCleskey (25) suggested that an electrostatic interaction between one ion bound to the channel and a second entering the pore occurs in Ca²⁺ channels. This results in a complex behavior of the conductance-activity relationship between the ions. An important demonstration of this interaction is a phenomenon called the AMFE. The AMFE occurs when a mixture of two permeant ions produces less current than either permeant ion alone. The AMFE is a complex phenomenon that depends on voltage and total concentration, as well as the intrinsic binding properties of the channel, and can be an important probe of ion-ion interactions in the open pore.

We studied the AMFE to examine how our mutations would affect ion-ion interactions in the open pore of Ca²⁺ channels. The experimental conditions were optimized to enhance our ability to detect changes in the AMFE. The AMFE was determined by measuring peak tail currents in the presence of various molar ratios of Ca²⁺ and Ba²⁺. Consistent with other reports (54–56), we found that the AMFE was greatest when tail currents were evoked at relatively positive potentials (−30 mV) and when the total divalent cation concentrations were kept low (i.e., 2 mM). I_Ba(tail)/I_Ca(tail) determined under these experimental conditions differs from I_Ba(max)/I_Ca(max) determined using protocols described in Fig. 4. Furthermore, under conditions that promote the AMFE (2 mM divalent concentration and tail currents measured at −30 mV), I_Ba(tail)/I_Ca(tail) values for the mutants do not follow the same trend as observed for G_Ba/G_Ca measured at −30 mV in Fig. 6. Together, these observations suggest that the extracellular divalent ion concentration is a critical parameter in determining the selectivity properties of the pore. For instance, notice in Fig. 11 that I_Ba(tail)/I_Ca(tail) for F1144K is similar to that of wild-type and that I_Ba(tail)/I_Ca(tail) for Y1152K is similar to that of FY/GK.

The AMFE for wild-type and mutant Ca²⁺ channels was measured using 2 mM mixtures of Ca²⁺ and Ba²⁺ such that the Ba²⁺/(Ba²⁺ + Ca²⁺) was 0.0, 0.3, 0.5, 0.7, 0.9, and 1.0 (Fig. 11). Note in Fig. 11 B that the normalized current for wild-type (open circles) decreases to 0.64 when Ba²⁺/(Ba²⁺ + Ca²⁺) = 0.7 before rapidly climbing to ∼1.2 as Ba²⁺/(Ba²⁺ + Ca²⁺) approaches 1.0. F1144G (squares) and FY/GK (triangles) do not exhibit an AMFE. The tail current amplitudes for F1144G and FY/GK decline almost monotonically with wild-type as Ba²⁺/(Ba²⁺ + Ca²⁺) progresses to 0.7, but fail to increase as Ba²⁺/(Ba²⁺ + Ca²⁺) approaches 1.0. In contrast to F1144G and FY/GK, Y1152K (solid circles) exhibits a robust AMFE, demonstrating that the AMFEs for FY/GK and perhaps F1144G are, indeed, attenuated. That the relative current amplitudes for FY/GK and Y1152K are indistinguishable when Ba²⁺/(Ba²⁺ + Ca²⁺) = 1 yet only Y1152K presents an AMFE, indicates that the I_Ba/I_Ca and the AMFE can be altered independently. This point is further exemplified in Fig. 11 C where the AMFE for F1144K (closed circles) is greater than the AMFE for wild-type (open circles). Notice that F1144K reaches a minimum value of 0.55 compared to 0.70 for wild-type. This enhanced AMFE is not likely to be linked to changes in the binding affinities of single Ca²⁺ and Ba²⁺ ions to the pore because the binding affinities changed very little for this mutant compared to the others (see Fig. 9). Together, these results suggest that the identity of the residue at position 1144 can accentuate or attenuate the AMFE.

DISCUSSION

Phe-1144 and Tyr-1152 substitutions reduce Ba²⁺ conductance by altering electrostatic and/or chemical interactions in pores occupied by multiple ions

Our data indicate that the reductions in Ba²⁺ conductance observed with F1144G, Y1152K, FY/GK, and F1144K do not arise from changes in the binding properties of single cations to the pore for the following reasons: First, if high affinity Ba²⁺ binding were inversely related to conductance, the mutant channels' reduction in Ba²⁺ conductance would be correlated with an increased binding affinity for individual Ba²⁺ ions and not the decreases observed in our experiments (Figs. 8 and 9). Second, the IC₅₀ for half-maximal block of Li⁺ currents through Y1152K channels by divalent cations is larger than it is for F1144G and F1144K (Figs. 8 and 9), yet unlike the Phe-1144 mutants, the G_Ba/G_Ca for Y1152K is decreased to the smallest extent (Figs. 4–7 and 10). Third, and perhaps most significantly, although the binding affinities of individual Ca²⁺ and Ba²⁺ ions to the selectivity filters of all four mutant channels are reduced, these reductions are not ion specific—i.e., the fold change in IC₅₀ values for half-maximal block of Li⁺ currents by Ba²⁺ is approximately equal to that by Ca²⁺ for all four mutant channels (Fig. 9). The small ion-specific differences that do appear in Fig. 9 cannot be responsible for reduced Ba²⁺ conductance because such differences are observed with Y1152K as well. Finally, like wild-type, the concentration for half-maximal block of Li⁺ currents through all the mutant channels is ∼35-fold lower for Ca²⁺ than it is for Ba²⁺. Thus, all the mutant channels would be expected to exhibit an AMFE similar to that of wild-type. Consistent with this prediction, the AMFE is preserved for Y1152K but it is not for F1144G and FY/GK, despite the fact that the effects on Li⁺ block are similar between all three mutants. Thus, contrary to theoretical models that base the differences between Ba²⁺ and Ca²⁺ conductance on the energetics of high affinity binding to the selectivity filter (25–28), our data indicate that high affinity interactions between the selectivity filter and individual Ba²⁺ or Ca²⁺ ions play only a minor, if any, role in determining the AMFE or the channel's preference for conducting one ion over the other.

Instead, we observe large, ion-specific effects when the mutant pores are occupied by multiple divalent cations (Fig. 10). It is likely that G_Ba/G_Ca for wild-type is ∼2 because a combination of electrostatic and/or chemical forces, all dictated by the pore geometry, act on multiple Ba²⁺ ions in ways that are quantitatively different from the way they act on Ca²⁺ ions. In contrast, G_Ba/G_Ca for the mutant channels approaches one because these forces act on Ba²⁺ and Ca²⁺ ions more equally. If the mutant selectivity filter is unable to discriminate between Ba²⁺ and Ca²⁺, one would predict that the AMFE would be flat, as indeed it is for F1144G and FY/GK.

Our observations that both whole-cell and unitary Ba²⁺ currents through F1144G channels are reduced compared to wild-type channels (Figs. 4–7, 10) are consistent with the results of Sather and colleagues (33), who found that the unitary conductance is proportional to the volume of the side chain introduced at position 1144. The positively charged lysine, whose Van der Waals volume is identical to that of phenylalanine, appears to be an exception to this rule. Based on the size of its substituted lysine residue, F1144K would be expected to exhibit conductance properties similar to those of wild-type. Our findings that Ba²⁺ conductance for F1144K resembles that of F1144G and not wild-type (Figs. 4–7, 10) are inconsistent with the premise that Ba²⁺ conductance is proportional to the side-chain volume at position 1144. Since Phe-1144 and Glu-1145 are neighboring amino acids that may interact (33), Glu-1145 may be held in a more restricted orientation when its neighboring residue is a positively charged lysine residue and in a less restricted orientation when its neighboring residue is a glycine residue. Thus, even though F1144G and F1144K both reduce Ba²⁺ currents, one would predict that there are subtle differences between the conductance properties of the two mutants. Such differences can be observed by comparing their respective AMFEs. When Phe-1144 is replaced with a glycine, the AMFE is flattened, whereas a lysine substitution enhances the AMFE. Thus, the AMFE is dependent on the identity of the amino acid residue at position 1144, suggesting that glycine and lysine substitutions at position 1144 reduce Ba²⁺ conductance via different mechanisms.

Phe-1144 and Tyr-1152 substitutions discussed in the context of contemporary structure-based models for Ca²⁺ channel permeation

Over the past decade an increasingly clearer picture has emerged of how the pore selectivity filter of the voltage-gated calcium channel confers high calcium selectivity while simultaneously supporting high rates of calcium flux. The EEEE locus is the critical player in this process, since it forms the calcium binding site. Nevertheless, our findings are consistent with a growing body of data suggesting that residues surrounding the EEEE locus also play important roles in fine tuning pore selectivity. Traditionally, two-site, three-barrier models based on measurable forces and binding energies have been used to describe the fundamental properties of ion selectivity and permeation through Ca²⁺ channels. These models cannot be used for structural studies because the forces and binding energies are not defined with realistic structural constraints. Newer models have been developed that reproduce many of the biophysical characteristics of ion permeation using structures thought to resemble the Ca²⁺ channel pore (57–61). Below, we discuss our experimental findings in the context of these new “structure-based” models.

The structural model of Lipkind and Fozzard (60), for example, can be thought of as a structural correlate to the “step” model of Dang and McCleskey (28) and the experimental findings of Kuo and Hess (62). In this model, the eight carboxyl groups from the EEEE locus form three binding sites: a central, high affinity divalent cation binding site formed by four of the carboxyl groups flanked by two low affinity divalent cation binding sites, each composed of two carboxyl groups. In the context of this model, our findings suggest that substitutions at positions 1144 and 1152 alter the interactions between one of the two low affinity glutamate pairs and Ba²⁺, but not Ca²⁺. A more detailed kinetic analysis of the mutants could reveal which of the two low affinity sites is altered.

That the selectivity filter has a defined volume is implied in the early barrier models (25,26,63), and that this volume is defined by the eight carbonyl oxygen atoms from the EEEE locus is explicit in contemporary models (11,57,59,61). Although the crystal diameters of Ca²⁺ and Na⁺ ions are nearly identical (2.00 vs. 2.04 Å, respectively), each Ca²⁺ ion carries twice as much countercharge as a Na⁺ ion. Thus, unlike Na⁺, Ca²⁺ is able to neutralize the highly charged selectivity filter without overcrowding the pore with counterions. Although the Ba²⁺ and Ca²⁺ ions carry the same charge, the ionic diameter of Ba²⁺ is ∼36% larger than that of Ca²⁺ (2.72 vs. 2.00 Å, respectively). Thus, Ba²⁺ ions would be predicted to exhibit a higher degree of crowding than Ca²⁺ ions, resulting in a faster exit rate and larger conductance for Ba²⁺. This “volume exclusion/charge neutralization” model can account for our findings if it is assumed that the substitutions at positions 1144 and 1152 altered the geometry and/or electrostatic environment of the selectivity filter such that it is more amenable to support occupancy by multiple, larger Ba²⁺ ions, whereas its ability to support occupancy by multiple Ca²⁺ ions changes little, i.e., if the selectivity filters of the mutant channels were to become less susceptible to “overcrowding” by Ba²⁺ ions. Such Ba²⁺-specific changes in the electrostatic-binding forces in the pore would predict that the mutant channel would exhibit a reduction in its Ba²⁺ conductance, whereas its Ca²⁺ conductance would be relatively unaffected.

Additional residues determine the permeability properties of several classes of voltage-gated Ca²⁺ channels

Here, we report that nonglutamate residues in the pore of L-type Ca²⁺ channels play critical roles in determining important properties of ion permeation. We originally hypothesized that the identity of the residues at positions 1144 and 1152 would confer subtype-specific characteristics on ion permeation. However, all the Ca_V2.1-like mutant channels tested, F1144G, Y1152K, and FY/GK, exhibited conductance properties that were more similar to Ca_V3 channels than Ca_V2.1 channels. Therefore, residues other than those at positions 1144 and 1152 are critical for determining the permeability properties of voltage-gated Ca²⁺ channels (33). Work by others supports this conclusion. For example, a Ca_V3.1 mutant where Asp-1145 is replaced by glutamate exhibits a I_Ba/I_Ca that is more reminiscent of Ca_V1.2 than Ca_V3.1 (64). Furthermore, substitutions as far as 100 residues upstream of Glu-1145 in Ca_V2.2 (N-type) channels reduce the channel's preference for passing Ba²⁺ currents over Ca²⁺ currents (32). Discovering how the glutamate and nonglutamate residues are arranged in the pore and how this structural arrangement produces an electrostatic and chemical environment conducive to ion permeation will undoubtedly be a challenging task. The consequences of this effort will greatly expand our understanding of the molecular details underlying ion permeation.