Mechanical Resistance of Proteins Explained Using Simple Molecular Models

Abstract

Recent experiments have demonstrated that proteins unfold when two atoms are mechanically pulled apart, and that this process is different to when heated or when a chemical denaturant is added to the solution. Experiments have also shown that the response of proteins to external forces is very diverse, some of them being “hard,” and others “soft.” Mechanical resistance originates from the presence of barriers on the energy landscape; together, experiment and simulation have demonstrated that unfolding occurs through alternative pathways when different pairs of atoms undergo mechanical extension. Here we use simulation to probe the mechanical resistance of six structurally diverse proteins when pulled in different directions. For this, we use two very different models: a detailed, transferable one, and a coarse-grained, structure-based one. The coarse-grained model gives results that are surprisingly similar to the detailed one and qualitatively agree with experiment; i.e., the mechanical resistance of different proteins or of a single protein pulled in different directions can be predicted by simulation. The results demonstrate the importance of pulling direction relative to the local topology in determining mechanical stability, and rationalize the effect of the location of importation/degradation tags on the rates of mitochondrial import or protein degradation in vivo.

INTRODUCTION

In the last few years, novel experimental techniques based on atomic force microscopy (AFM) have made it possible to observe the force-induced unfolding of single proteins (1). Most of the proteins studied experimentally so far display varying degrees of mechanical resistance: i.e., when two atoms are pulled apart at a given rate, the applied force must exceed a threshold for unfolding to occur. Although it was initially believed that mechanical unfolding probes the same pathways as chemical denaturation (2), later experimental work clarified that this was not the case (3–5).

Now that many proteins have been mechanically unfolded via simulation and experiment, one may begin to ask: what are the main factors that govern mechanical strength? As a consequence of the local nature of applied force, the type of secondary structural motif between the points of extension is thought to be an important determinant of mechanical resistance in proteins, with β-sheet structures being more mechanically resistant than all α-helical ones (5–10). Importantly, the direction in which the force is applied onto these features (4,11) has also been shown to have profound effects on the apparent mechanical strength of two proteins, E2lip3 and ubiquitin. These results and other dynamic force spectroscopy studies suggest that the energy landscape for mechanical unfolding is highly anisotropic and that mechanical unfolding occurs through pathways rarely traversed under thermal or chemical unfolding conditions. The difference in unfolding mechanism and the anisotropy of the mechanical unfolding landscape may explain how proteins which are thermodynamically and/or kinetically stable are degraded in vivo at a significantly faster rate than would be expected. For example, recent experimental and simulation studies suggest that barnase, a kinetically stable protein, is rapidly imported into a mitochondrion via a different pathway to that found under chemical denaturing conditions (12,13).

To assess the effect of pulling geometry on mechanical strength in further detail, it is necessary to fully characterize the unfolding energy landscape by extending the same protein through many different geometries. However, most proteins studied to date by this technique have utilized recombinant tandem arrays of homopolymers and this limits the extension geometry to that applied between the N- and C-termini. Other extension geometries are possible but limited (E2lip3 is specifically labeled with a gold reactive tag at a single site (4); ubiquitin can form polymers between its C-terminus and the side chain of one of four lysine residues (11); and lysozyme has been linked by novel disulphide bonds (14)). A full experimental investigation of the mechanical unfolding energy landscape is thus a formidable task. By contrast, molecular dynamics simulations (15,16) are not constrained by these experimental limitations and, therefore, can allow unprecedented insight into the mechanical unfolding landscape at a resolution higher than that possible using experimental techniques. Simulation, however, relies on approximate models, and the accessible timescales are much shorter than those probed experimentally, particularly if detailed models are employed. The timescale problem is particularly relevant for AFM experiments that probe the non-equilibrium response of a molecular system to an applied force and depend on the rate of loading the external force (17). Constant velocity pulling experiments performed on E2lip3 (4) and ubiquitin (11) in multiple directions have been qualitatively reproduced in silico using all-atom steered molecular dynamics (SMD). In these simulations the termini are pulled apart at speeds of six or so orders-of-magnitude faster than in experiments. Despite the disparity in timescales, these high-speed methods correctly predict mechanically hard and soft directions within a single domain for both implicit (for E2lip3) and explicit (for ubiquitin) solvation models.

Most simulations of forced unfolding published so far have been performed using SMD (15), which is analogous to constant velocity experiments. In both constant velocity experiments and simulations, the applied force is monitored as a function of the end-to-end distance. The unfolding of the protein (or in general, the crossing of a barrier) corresponds to a peak in the observed force.

The prevailing two-state paradigm of forced unfolding is that the unfolding rate (or inverse unfolding time) depends exponentially upon a constant applied force (see Eq. 2 below). However, out of convenience, most AFM unfolding experiments, to date, have been performed by pulling the cantilever at a constant velocity, i.e., by applying a time-dependent force to the protein. Consequently, when a concatamer is unfolded at constant velocity, the instantaneous force varies in time because the effective concatamer-cantilever compliance changes from one event to the next as more unfolded material is released (18). Moreover, the nonlinear polymer elasticity of the unfolded material leads to a compliance that changes during extension even before an unfolding event (19). Hence, fitting unfolding data (typically the distribution of unfolding forces) to a two-state model involves a complicated procedure that includes domain number and the compliance of cantilever and unfolded polymer. This procedure is soluble, but involved (18). By contrast, when a constant force is imposed on proteins as is now experimentally possible (20–22), compliance effects are irrelevant, and it is conceptually and practically much easier to extract model parameters by fitting to the distribution of unfolding times. However, we note that even in this case, the unfolding time of the next domain increases as successive domains unfold, and such effects must be taken into consideration for accurate interpretation of the experimental data (although this has not been noted previously (21)). This is not an issue, of course, for single domain experiments. A constant force is easily applied in a simulation (constant force molecular dynamics, or CFMD). In both constant force experiments and simulations, the end-to-end distance as a function of time shows plateaus, corresponding to metastable states under force, and phases of rapid increase revealing the overcoming of a barrier and possibly the complete unraveling of the protein. Discrete steps signify domain unfolding events or partial unfolding to intermediate states. Constant force simulations have the advantage that the metastable state, from which forced unfolding occurs, can be stabilized for very long times with an appropriate force, and thus, can be characterized. For example, CFMD simulations led to the observation and full characterization of the relevant unfolding intermediate of I27 (3).

Hence, for a single domain, constant force (CFMD) and constant velocity (SMD) techniques are, in principle, equivalent. However, constant force simulations are easier to interpret because the two-state kinetic model of unfolding (see Eq. 2 below) can be applied directly without the need to consider a changing compliance. The relevant quantity in constant force simulations/experiments is the unfolding time—i.e., the average time before the protein reaches a certain length, typically just beyond the largest unfolding barrier, at which it can be considered to be unfolded; this time depends only weakly on distances greater than that of the unfolding barrier. In constant velocity simulations/experiments, the relevant quantity is the maximum of the force; the fluctuations of the force around the maximum are highly dependent on the cantilever spring constant and introduce uncertainty into the estimation.

All-atom simulations are still computationally expensive, making simulation of the mechanical response of a single protein extended through a wide variety of geometries currently unfeasible if a broad range of forces (or speeds) is explored and statistically meaningful results are to be obtained. Here a computationally efficient coarse-grained Gō model, with an additional sequence-specific term to describe the backbone dihedral angles of the protein, is shown to be very suitable for these kinds of studies. Gō models have been widely used to study folding mechanisms (23–28), but their relevance to the folding of real proteins is questionable, since the non-native state in Gō models resembles a polymer in good solvent with non-native interactions that are usually set to be neutral or even repulsive (29).

Because mechanical unfolding simulations are initiated from the native state, the topology of which is an important determinant of mechanical resistance, it might not be surprising that Gō models, which are constructed from the knowledge of a protein's native state, give good agreement with some of the experimental results (30–32). Here we use a very simple structure-based model that encapsulates the properties of the native state and show that, by comparison with all-atom simulation and available experimental results, simulation can predict exactly the relative mechanical strength of proteins as a function of pulling direction and protein topology. In the following, we use the expression “pulling direction” to indicate the pair of points on which the force is applied.

METHODS AND TECHNIQUES

Choice of model proteins

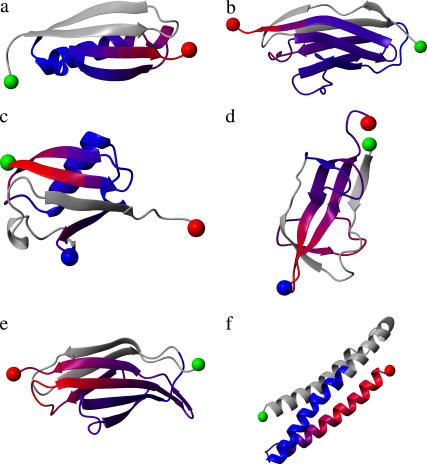
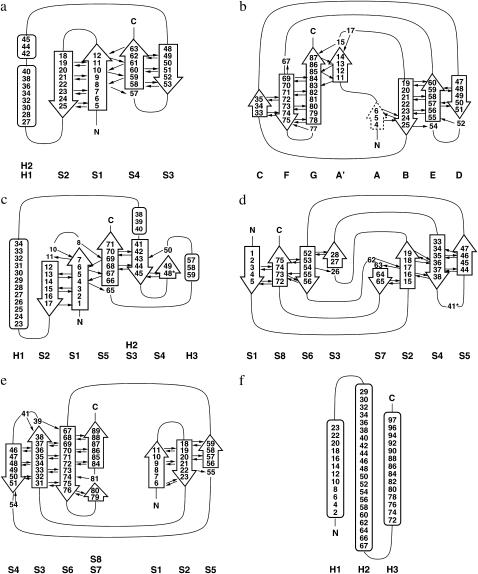
The six single-domain proteins chosen for study in this article have all been experimentally characterized for mechanical resistance, and their structures are available. These are I27 (PDB ID 1tit (33)), ubiquitin (1ubq (34)), protein L (1hz6 (35)), E2lip3 (1qjo (36)), tenascin (1ten (37)), and spectrin (1aj3 (38)). This set of proteins covers a broad spectrum of protein topologies from all β-sheet proteins with immunoglobulin-like β-sandwich folds (I27 and tenascin) or the barrel-sandwich hybrid topology of E2lip3, to α + β proteins with β-grasp (ubiquitin-like) folds (ubiquitin, protein L), to all α-proteins with spectrin-repeat-like folds (spectrin). The structure of these proteins is shown in Fig. 1 and topology diagrams in Fig. 2.

FIGURE 1.

Structure and mechanical strength of the six test proteins: (a) protein L, (b) I27, (c) ubiquitin, (d) E2lip3, (e) tenascin, and (f) spectrin. Blue to red represents soft to hard directions relative to that domain only when pulled from the N-terminus (green sphere), or C-terminus (red sphere) in the case of ubiquitin. Gray denotes regions not pulled. Experimentally E2lip3 and ubiquitin have been pulled from their N-/C-termini, and in a second direction, N-41 and C-48, respectively (denoted by the blue sphere). Figure generated using the program MOLMOL (54).

FIGURE 2.

Topology diagrams of the six test proteins: (a) protein L, (b) I27, (c) ubiquitin, (d) E2lip3, (e) tenascin, and (f) spectrin. Black arrows indicate inter-β-strand hydrogen bonds.

Molecular dynamics simulations

Molecular dynamics simulations were performed using the CHARMM (version ≥ 31) molecular dynamics simulation package (39). In both models, each protein was equilibrated for a period of 50 ns with a conformation selected every 1 ns as a starting conformation for the constant force simulations. For each of the 50 starting configurations, two atoms were selected to which a constant force was applied, the force being directed as the distance vector between the two selected atoms. On a 3-GHz Pentium processor, 1 ns of simulation took 1.5 min of CPU time for the coarse-grained Gō model and 2.5 h for the detailed, transferable EEF1 model.

All-atom model simulations (EEF1)

All-atom simulations were performed using an implicit model for the solvent (EEF1) (40). Implicit solvent models are sufficiently accurate and avoid artifacts due to the relaxation of the explicit solvent, which might be slow relative to the fast conformational changes induced by the external force (16); moreover, the EEF1 implicit solvent is computationally efficient and allowed us to simulate cumulatively several microseconds. All of the full-atomistic molecular dynamics simulations were performed at 300 K temperature using a Nosé-Hoover thermostat, imposing a holonomic constraint on the bonds involving hydrogen atoms, using an integration timestep of 2 fs.

Gō model simulations

The Gō model simulations were performed using the C_α model proposed by Karanicolas and Brooks (28,41). The protein is represented as a series of C_α atoms, each of which was assigned a mass of the corresponding amino acid. Native contacts were defined if the side-chain contacts between neighboring residues were within 4.5 Å or if a pair of amino acids were directly hydrogen-bonded, and all non-native contacts were subject to a repulsive interaction (see (28) for details). The interaction energy of pairs of atoms forming native contacts was a modified Lennard-Jones function containing an attractive r⁻¹⁰ term and repulsive r⁻¹² and r⁻⁶ terms to represent a desolvation penalty; the minimum of the energy corresponds to the native distance between the pair of atoms, and the maximal pairwise interaction strength is set to the contact energy from the pairwise contact potential of Miyazawa-Jernigan (42) for this pair. A pairwise term taking into account the relative orientation of pairs of residues involved in hydrogen bonding was also included (28). Another original feature of this Gō-like model is a sequence-specific term related to the backbone dihedral angles of the protein (28). The topology and parameter files were generated using the MMTSB web server (http://mmtsb.scripps.edu/webservices/gomodel.html). Holonomic constraints were applied to the C_α bonds, allowing an integration timestep of 10 fs. The temperature was maintained at 300 K using a Langevin thermostat (friction coefficient 0.1 ps⁻¹). The model of Karanicolas-Brooks is, in all senses, a Gō-like model. In a previous article (29), we have considered a number of different Gō-like models with uniform or non-uniform energy scales, with various assumptions about the non-native interactions, including all-atom and C_α models. We have found that the Karanicolas-Brooks model works better than others in the sense that it describes the free energy surface of a peptide similarly to an all-atom transferable model (such as CHARMM+EEF1). However, some characteristics, such as a very unstructured and expanded denatured state, are common to all the Gō models and quite different from the transferable CHARMM-EEF1 model.

Calculation of unfolding time

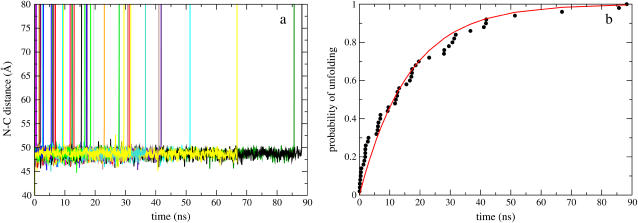
During the simulation, the distance between the selected atoms was monitored as a function of time. A well-defined barrier was assumed when the distance between the two ends fluctuated around a constant value for a long period. When the protein unfolded, the end-to-end distance increased very rapidly (Fig. 3 a). The unfolding time for each structure was defined when the end-to-end distance reached 110% of the length of the unfolding barrier (ie., the last plateau in the extension-time profile before the protein unravels completely), or, in the absence of a barrier, 50% of the fully stretched unfolding length. The unfolding time was estimated from (43)

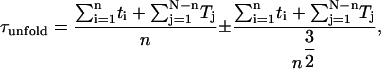(1)

where t_i is the unfolding time for each of the n unfolding events, and T_j the maximum simulation time for each of the N−n structures that remained folded, and N = 50, the total number of structures pulled for each geometry and force.

FIGURE 3.

(a) I27 N-C extension as a function of time when a constant 150 pN force is applied using the Gō model. A single unfolding barrier can clearly be seen at 49 ± 2 Å, from which unfolding occurs (N-C distance in the native state is 42 Å). (b) The probability of unfolding fits a single exponential 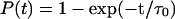with τ₀ = 16 ns.

Assuming that a protein under force behaves like a two-state system and that the distance to the transition state x_u remains fixed with applied constant force F, the average unfolding time τ depends exponentially on the force,

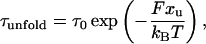(2)

where τ₀ is the native lifetime in the absence of a force, k_B is Boltzmann's constant, and T is the temperature.

RESULTS

Simulation predicts the mechanical resistance of protein domains

Both all-atom and coarse-grained models reveal the same unfolding intermediate for I27

To verify that the coarse-grained Gō model and the all-atom (EEF1) model provide consistent results in terms of the predicted unfolding pathway, the mechanical resistance of I27 (Figs. 1 and 2) was investigated, since this protein has been intensively studied by both experiment and simulation (2,3,15,44–46). The mechanical unfolding of this protein was simulated using each model by applying a constant force to the N- and C-termini of this domain.

The mechanical unfolding behavior of I27 observed using the Gō model is shown in Fig. 3 a. For a constant force of 150 pN applied to the N-C termini, the molecule's extension displays a single very clear plateau, which is the typical behavior expected from an activated barrier-crossing due to thermal fluctuations. Notice that for I27, the plateau is observed at an extension of ∼7 Å relative to the native state (native N-C distance ∼42 Å) with the A-strand dissociated from the main core of the protein (not shown): this means that a slightly elongated conformation is more stable than the native state under a very small pulling force, and the barrier between these two states, if any, is small. Repeating the simulation 50 times shows that the distribution of unfolding times (Fig. 3 b) is clearly exponential, hence a large number of independent simulations are necessary to estimate the unfolding time reliably. Importantly, unfolding the same protein using the EEF1 model shows the same forced-unfolding mechanism, with a matching plateau observed at ∼7 Å extension (3). This has been previously reported and confirmed by experiment to involve the unfolding of the A-strand from the β-sandwich to form a kinetically stable unfolding intermediate (3). This result demonstrates that the Gō model captures all of the important structural features of the I27 forced unfolding mechanism, highlighting the importance of the mechanical clamp region of strands A′ and G that endow the mechanical resistance of this domain.

Both models predict relative mechanical strength of six model proteins experimentally studied by AFM

The high mechanical strength of I27, which is a consequence of the shearing of directly hydrogen-bonded parallel terminal β-strands, may allow the forced unfolding of the protein to be predicted relatively easily. To further test the validity of Gō models to simulate the mechanical unfolding of proteins, and to examine the advantages and drawbacks of their approach over all-atom methods, the mechanical unfolding of a wide variety of proteins with different topologies was examined over a wide range of applied constant forces. The proteins selected for study were protein L, I27, ubiquitin, E2lip3, tenascin, and spectrin (see Figs. 1 and 2 for diagrams of their structures and topologies). These proteins, which have diverse structure, have all been studied experimentally using the AFM and found to exhibit a variety of unfolding behaviors (see Table 1).

TABLE 1.

The set of proteins studied ranked according to the unfolding force measured experimentally and according to the unfolding rate estimated in the simulations with the two different models

Class	Experiment	Ref.	Gō	τunfold (ps)	EEF1	τunfold (ps)
Hard	Ubiquitin (N-C) 203 ± 35 pN at 400 nm s−1	(11)	Protein L	5.0 × 106	Protein L	2.9 × 104
	I27 204 ± 26 pN at 400–600 nm s−1	(2)	Ubiquitin (N-C)	1.7 × 105	Ubiquitin (N-C)	3.0 × 103
	Protein L 152 ± 5 pN at 700 nm s−1	(5)	I27	1.8 × 104	Ubiquitin (C-48)	1.6 × 103
					I27	520
Intermediate	E2lip3 (N-41) 177 ± 3 pN at 700 nm s−1	(4)	E2lip3 (N-41)	1.4 × 103	Tenascin	29
	Tenascin 137 ± 12 pN at 200–600 nm s−1	(53)	Tenascin	340	E2lip3 (N-41)	21
	Ubiquitin (C-48) 85 ± 20 pN at 300 nm s−1	(11)	Ubiquitin (C-48)	90
Soft	Spectrin 25-35 pN at 300 nm s−1	(6)	Spectrin	54	E2lip3 (N-C)	4.9
	E2lip3 (N-C) <15 pN at 600 nm s−1	(4)	E2lip3 (N-C)	47	Spectrin	1.9

Although the exact order is different, the three methods rank the proteins in the same three classes of mechanical resistance (with one exception, ubiquitin (C-48) which is found to be “hard” with the EEF1 model).

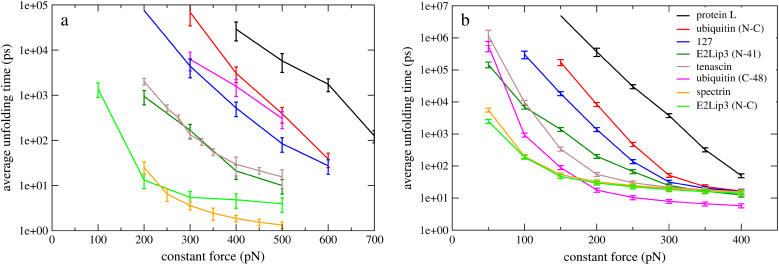
The unfolding time as a function of force for the two different force fields was ascertained for each protein when force was applied via their N- and C-termini. Additionally, E2lip3 and ubiquitin were pulled in a second direction, as has been performed experimentally. (Below E2lip3 (N-C) and ubiquitin (N-C) denote these proteins when pulled from their N- and C-terminal C_α atoms, E2lip3 (N-41) E2lip3 when pulled from N-terminal and residue 41 C_α atoms, and ubiquitin (C-48) ubiquitin when pulled from C-terminal and residue 48 C_α atoms) Fig. 4 shows the average unfolding times of each domain for the detailed, transferable EEF1 model (Fig. 4 a) and the more coarse-grained, structure based Gō model (Fig. 4 b). Regardless of the model, each of these proteins displays a broad range of mechanical resistance, dependent upon the applied force. Remarkably, both models predict similar behavior for individual proteins and these observations correlate well with experimental measurements of protein mechanical strength. Protein L, ubiquitin (N-C), and I27 unfold slowly for a given force, indicating a large unfolding barrier. For these proteins the logarithm of the average unfolding time is approximately linear in force over a broad range of forces (400–600 pN and 150–300 pN for the all-atom and coarse-grained model, respectively) implying two-state unfolding with a transition state that remains stationary with applied force (Eq. 2). At larger forces, the barrier to unfolding is completely neutralized; the logarithm of the unfolding time tends to an asymptotic value and there is little variation for different proteins, since the internal friction provides the only means of resistance. Conversely, spectrin and E2lip3 (N-C) unfold rapidly and show clear nonlinearity over the entire range of forces studied. This indicates either no barrier, or a relatively small unfolding barrier that moves with applied force, so that the simple two-state model does not hold. Finally, E2lip3 (N-41), tenascin, and ubiquitin (C-48) show some linearity in the low force regime, which indicates a shallow unfolding barrier that is quickly surmounted at higher forces.

FIGURE 4.

The average unfolding time of six different protein domains under force pulled from their N-C termini using (a) a detailed, transferable EEF1 model and (b) a coarse-grained, structure-based Gō model. E2lip3 and ubiquitin are pulled in a second direction, revealing qualitative agreement with experiment. Note the broad range of forces over which the mechanical ranking of the proteins can be defined. The error bar for protein L at 150 pN in the Gō model has been removed for clarity.

From the curves in Fig. 4, a and b, a ranking in terms of mechanical stability is clearly possible, although not unique—since the slopes of the curves are not identical for different proteins. For a force F_min at which the unfolding time for all proteins can be reliably estimated, taken to be the lowest force at which unfolding events are observed in the strongest protein (e.g., F_min = 400 pN for the EEF1 model and F_min = 150 pN for the Gō model), τ_unfold(F_min) characterizes mechanical stability, with larger τ_unfold(F_min) signifying greater stability. Table 1 compares the rankings of the proteins for the two simulation models (according to unfolding times) with experimental results (according to unfolding force for constant speed experiments). Although absolute rates cannot be compared directly with experiment because of the approximate force fields and the absence of a realistic solvent viscosity, it is striking that both models agree qualitatively with experiment. The agreement is even more evident if we rank the proteins into three classes: hard, soft, or intermediate.

Protein L, ubiquitin (N-C), and I27 are found to be mechanically hard. These domains have very different structures (Figs. 1 and 2), but all three proteins withstand significant mechanical force (>100 pN at pulling speeds >100 nm s⁻¹) when pulled from their termini experimentally (5,21,47). Protein L and ubiquitin have a β-grasp (ubiquitin-like) fold, whereas I27 has a classic Ig-like fold. In each case, the terminal strands of the protein are parallel and directly hydrogen-bonded (assuming the A-strand plays no role in the mechanical stability of I27), leading to a longitudinal shearing action of β-strands parallel to the applied force. These data confirm, therefore, that this arrangement of strands and their orientation relative to the force (i.e., the end-to-end vector) is optimal for mechanical stability.

Spectrin and E2lip3 (N-C) belong to the mechanically soft class. Spectrin has been shown to unfold experimentally at very low forces (25–80 pN at 300–3000 nm s⁻¹) (6,9,48,49); its all-α-helical structure allows the force to unravel the helices in a sequential manner with each hydrogen bond being loaded in turn until mechanical failure. E2lip3, by contrast, is an all β-sheet protein. Its mechanical lability can be explained, however, by considering the direction of the force vector relative to the orientation of the directly hydrogen-bonded terminal β-strands. The application of force to the two terminal β-strands loads each hydrogen bond in turn, leading to consecutive failure and the unzipping of the protein at low force (<15 pN at 600 nm s⁻¹ (4)).

E2lip3 (N-41) and tenascin fall into the intermediate class, showing some mechanical strength over the range of forces studied. Once again, these proteins are mainly β-sheet (Fig. 1). E2lip3 (N-41) is highly resistant to extension although the force is applied onto the domain at points significantly separated through space. Despite this, both extension points are isolated from the rest of the structure by hydrogen-bonded clamps formed by the β-sheets (strands 1, 3, 6, and 8 for the N-terminus and strands 2, 4, 5, and 7 for C_α 41; see Fig. 2 d). These clamps must be disrupted, resulting in higher mechanical resistance. For tenascin, the intermediate stability of this domain can be readily explained since the loading force is applied to the terminal β-strands, but these are not directly hydrogen-bonded. Finally, ubiquitin (C-48) falls into the intermediate class when using the coarse-grained Gō model, but is hard-class when using the transferable EEF1 model. Force is applied onto ubiquitin (C-48) at distal ends of a pair of directly hydrogen-bonded β-strands, which should intuitively result in high mechanical strength. However, the geometry of these strands is such that the force is not applied parallel to these strands, resulting in less mechanical resistance than when the protein is pulled between its N- and C-termini. The reason for the apparent discrepancy in classification between the models is that, although both reveal identical near-native barriers (<10 Å) in C-48 extension, the EEF1 model reveals successive barriers up to 25 Å from the native state that form the main rate-limiting step to unfolding. One of these long-living intermediates is characterized by the slipping of the β-strand 3 by four residues down β-strand 5; this metastable structure resists the external force, thanks to non-native backbone hydrogen bonds. Since non-native contacts are not taken into account in the more coarse-grained Gō model, these potential barriers to unfolding are disregarded. In this specific case, the Gō model better reproduces the experimental result—suggesting that only native interactions are important when considering the origins of mechanical strength.

Taken together, the data show the remarkable result that, with one exception, both models can predict the experimental class of mechanical resistance for each protein.

We remark here that, although the slopes of the curves in Fig. 4 are different and thus, at different forces, the ranking might be different, this is not the case if one chooses an interval of forces where the curves are approximately linear. For weak proteins, where the relations among the logarithm and unfolding time and force are not linear, the ranking is more ambiguous.

Mechanical topology of I27

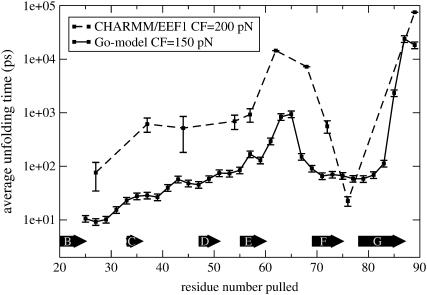
Experimentally pulling proteins in various directions has thus far relied upon natural but highly specific oligomerization or chemical modification strategies, which limit the number of possible pulling directions. However, to delineate the role of topology in mechanical strength, one must pull the same protein in many different directions. Although the number of pulling directions that can be explored in experiments and all-atom simulations is limited (and hence pulling sites are carefully chosen), Gō models offer the possibility to explore all pulling directions for different proteins. To investigate the utility of Gō models for such experiments, both EEF1 and Gō models were used to pull I27 in numerous geometries between its N-terminus and various other C_α atoms, and the results analyzed statistically in a detailed and systematic manner. For the coarse-grained model, the N-terminus was fixed, whereas all residues from 25 to 89 (with an increment of 2) were pulled. Because the all-atom EEF1 simulations are computationally more expensive, only 10 geometries were sampled compared with 33 for the coarse-grained Gō model. In Fig. 5, the results from the two models are compared. The direct comparison of folding times at given forces is not meaningful, because of the differences between the models, and in particular because of a major role played by the solvent viscosity, which is here much lower than the experimental one due to the low values of the friction coefficient used. However, the unfolding profiles for the two models are strikingly similar. Both models predict the N-C geometry to be the most mechanically stable, with the stability arising from the mechanical clamp region of strands A′ and G. Pulling between the N-terminus and midway across the loop of strands E and F (residues 63 and 65, Fig. 2 b) is predicted to be the second most mechanically resistant direction. In terms of topology, this is intuitive, since, upon detachment of the A strand, the force is transmitted via a shearing action across strands A′, G, and F. However, the mechanical stability is lower in this case because the resistance depends on the persistence of all three strands, resulting in a greater likelihood of unfolding compared with extension between the N- and C-termini in which force is loaded onto only two strands. Finally, one may have expected a third peak to appear when unfolding from the N-terminus and midway between the C and D loops. However, when I27 is pulled in this geometry, detaching of the A-strand loads the mechanical force orthogonally to all β-strands, leading to the unzipping of the domain at low force. Finally and most importantly, the mechanical unfolding profiles of the EEF1 and Gō models are identical, demonstrating the utility of Gō models to reveal the mechanical details of a protein's topology.

FIGURE 5.

The unfolding time profile of the detailed, transferable EEF1 model (CF = 200 pN) and coarse-grained, structure-based Gō model (CF = 150 pN), pulling I27 from the N-terminus and other C_α atoms within the domain.

Mechanical profile of other domains

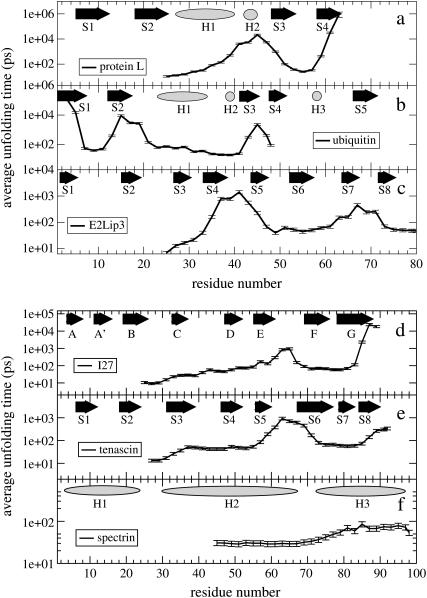
The effect of extension geometry on the mechanical strength of the other five test proteins, assessed in detail using the coarse-grained model, is shown in Fig. 6 and graphically depicted in Fig. 1. Each protein was unfolded multiple times at a constant force of 150 pN by fixing its N-terminus (for ubiquitin, the C-terminus was fixed in accordance with the experimental results (11)) and pulling all other residues apart.

FIGURE 6.

Unfolding time as a function of the pair of C_α atoms to which the constant force (150 pN) is applied. In abscissa is the C_α atom to which force is applied, while the N-terminus is kept fixed (except for ubiquitin where the C-terminus is kept fixed). Along the top of each unfolding time profile is the native secondary structure; β-strands are shown as arrows, α-helices as ellipses.

For all proteins, the mechanical resistance is correlated in a nontrivial manner with the topology of the protein and the imposed pulling geometry relative to these structures. The similarity in the unfolding time profiles of I27 and tenascin (Fig. 6, d and e), which both have the same Ig-like β-sandwich fold, underlines the relationship between mechanical resistance and native topology. However, the lower unfolding time for tenascin, when pulled from its termini, suggests that this domain is mechanically weaker than I27—probably because the terminal strands are not directly hydrogen-bonded as they are in I27.

The link between mechanical strength and β-strand topology is also evident in protein L (Fig. 6 a) and ubiquitin (Fig. 6 b). For both these proteins, the longest average unfolding time (greatest mechanical strength) occurs when the proteins are extended between the N- and C termini, which form a pair of directly hydrogen-bonded parallel β-strands. However, application of force to opposite ends of other pairs of distal β-strands also results in high mechanical strength (N-terminus and the loop between the helix and strand 3 in protein L, for example). For ubiquitin, as one progresses away from the N-terminus down strand 1, the average unfolding time steadily decreases. Following the structure up β-strand 2, there is a recovery of mechanical strength in the domain, due to hydrogen-bonding between strands 1 and 2. Passing through helix 1, the domain becomes mechanically soft until β-strand 3 is encountered (hydrogen-bonded to β-strand 5), where the domain once again increases in mechanical strength. Note that the mechanical peaks all occur when the force is applied parallel to hydrogen-bonded β-strands. These Gō model simulations clearly show the anisotropy of force response for this protein and reproduce the experimental observation that ubiquitin displays greater mechanical strength when extended by the N- and C-termini than when extended by the C-terminus and residue 48 (11).

Although β-sheet-rich proteins are mechanically resistant, with the unfolding time profile clearly related to the arrangement of β-strands relative to the orientation of the applied force, all α-helical proteins behave differently. For example, the all α-helical protein spectrin has a very low (N-C) mechanical resistance, which agrees with experiment (6,49) and previous simulation (7,50); here we also show that spectrin's mechanical resistance is not highly dependent upon which pairs of residues are pulled apart (Fig. 6 f).

Though β-strand topology can be used to explain mechanical strength in terms of shearing and peeling of hydrogen-bonded strands, in more topologically intricate proteins such as E2lip3 (a barrel-sandwich hybrid fold) it is not always obvious which geometry will be the most mechanically stable. Here, we show that the most mechanically stable pulling geometries found for E2lip3 are when this protein is extended between the N-terminus and the loop connecting β-strands 4 and 5 or the N-terminus and the loop between strands 7 and 8 (Fig. 6 c). The latter case applies force at opposite ends of directly hydrogen-bonded β-strands and is expected to be mechanically strong. The former geometry is identical to that tested experimentally, which also shows high mechanical strength (4). A coarse-grained Gō model thus reproduces all currently available experimental data for the mechanical unfolding behavior of these proteins.

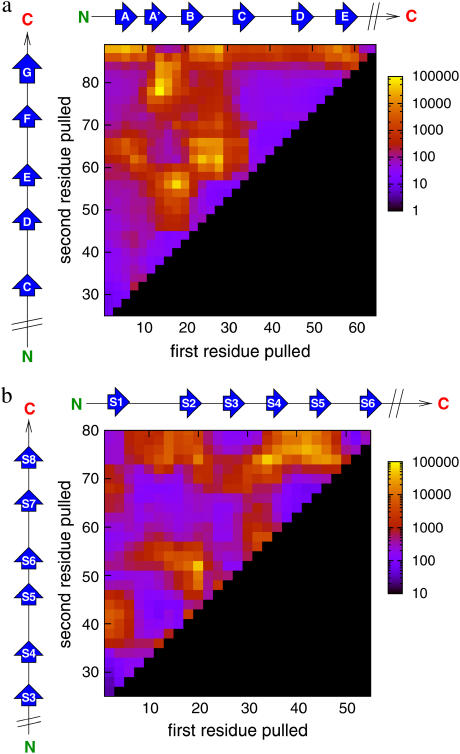
Complete unfolding landscape for I27 and E2lip3

To further explore the role that topology plays in defining mechanical strength, two of the proteins, I27 and E2lip3, were pulled in all possible directions—i.e., by not fixing either of the two termini, thus exploring the entire mechanical landscape of these proteins (Fig. 7). The mechanical landscape of I27 is remarkable in its simplicity: high mechanical resistance only occurs when the force induces the longitudinal shearing of β-strands. This longitudinal shearing can occur between points that are on the same sheet (the loops between A′B and DE), on different sheets (the C-terminus of the G-strand and the DE loop), or on the loops that link each sheet (BC and EF). By contrast, it is soft when force is applied orthogonally to β-strands (e.g., when force is applied between the BC and DE loops, between CD and FG loops, or between the N-terminus and the FG loop). These directions identify the Achilles'-heel of an otherwise mechanically hard protein. Interestingly, these soft directions are orthogonal to one end of a set of β-strands, supporting the hypothesis that mechanical resistance is topologically determined. Since I27 is linked by its terminal ends to form a tandem array of similar domains in titin, this protein thus has an ideal topology to endow mechanical resistance.

FIGURE 7.

Gō models reveal anisotropy in the mechanical unfolding landscape of (a) I27 (CF = 150 pN) and (b) E2lip3 (CF = 100 pN). Yellow to blue colors denote geometries of high to weak mechanical resistance, black denotes regions not pulled. Scale is in picoseconds.

E2lip3, by contrast, has a more complex mechanical unfolding landscape. A weak response is found when force is applied orthogonally to β-strands (for example, between the N- and C-terminus) or when loops are peeled apart. This is presumably because each element of mechanical resistance is loaded and fails sequentially. On the other side, E2lip3 is highly resistant to extension under application of force between pairs of residues (such 20 and 50) which are in loops connecting both sheets together. Extension of these strands, therefore, implies the shearing apart of a large number of hydrogen bonds.

As shown above and by previous experiments and simulations, E2lip3 unfolds at significant forces when extended between the N-terminus and residues in the loop connecting strands 4 and 5 (residues 39–43). Such an extension subjects the entire domain to a longitudinal shearing force and may endow mechanical strength when this domain is in a functional complex. Surprisingly, E2lip3 shows greater mechanical stability when extended between the C-terminus and residue 41 than when extended by the N-terminus and residue 41, despite their close proximity. This observation may be of functional importance. In the pyruvate dehydrogenase complex of Escherichia coli, E2lip3 shuttles an acetyl group (attached via a lipoyl moiety to residue 41) between active sites in the inner icosahedral core and the outer spherical shell (51). E2lip3 is connected to the outer shell by a C-terminal linker. Thus, any force applied onto this domain during its functional cycle will be through an extension geometry in which this domain is mechanically robust. Some of these highly force-resistant geometries shown by this analysis may be a result of their function, while more mechanically labile geometries may be utilized to allow rapid protein turnover in vivo.

CONCLUSIONS

The data presented above demonstrate that coarse-grained, structure-based (C_α/Gō) and detailed, transferable (all-atom/CHARMM/EEF1) models give consistent results, both in terms of ranking proteins according to their mechanical resistance and pulling proteins in different directions. Strikingly, a structure-based coarse-grained model predicts the experimental class of protein mechanical strength. The Gō model employed in this work uses sequence-specific energy couplings and hydrogen bonds are specifically represented, whereas other more simple models that use a uniform energy scale (52) have found discrepancies in the strength of domains between simulation and experiment. The data demonstrate that structure-based models, particularly when the relative strength of native interactions is realistically included such as in the Karanicolas-Brooks model employed here, can predict the relative mechanical resistance of proteins, in agreement with all the experimental results available to date.

The simulations shown here delineate the role of topology and the importance of the directions of hydrogen bonds relative to the direction of the applied force in determining mechanical strength. Force applied parallel to directly bonded β-strands proves to be the most mechanically stable geometry, while forces applied across α-helices or orthogonal to one end of a set of β-strands prove to be mechanically soft. These results are particularly striking when investigating the entire topological unfolding landscape of I27 and E2lip3. Here, not only did the application of force to the N- and C-termini of I27 have high mechanical resistance, but also applying the force to any other set of directly hydrogen-bonded β-strands, be they parallel or antiparallel, also resulted in significant mechanical resistance. Moreover, perhaps the most interesting result of these simulations is that many soft directions or Achilles'-heels can be identified in an otherwise mechanically stable protein. Biology, therefore, has many features to exploit to define the mechanical properties of proteins, including the number of domains in a heteropolymer, and linker lengths such as PEVK regions in titin and the scaffold stiffness in the cytoskeleton or extra cellular matrix; but perhaps the most important determinant of mechanical resistance is the topology of the protein and the geometry of the force vector applied to it.