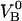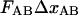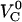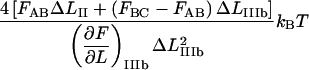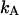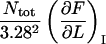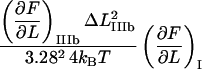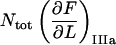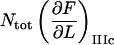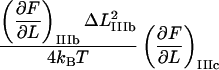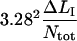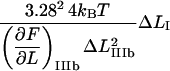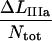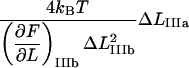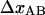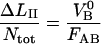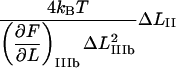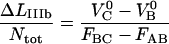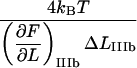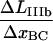A Sticky Chain Model of the Elongation and Unfolding of Escherichia coli P Pili under Stress

Abstract

A model of the elongation of P pili expressed by uropathogenic Escherichia coli exposed to stress is presented. The model is based upon the sticky chain concept, which is based upon Hooke's law for elongation of the layer-to-layer and head-to-tail bonds between neighboring units in the PapA rod and a kinetic description of the opening and closing of bonds, described by rate equations and an energy landscape model. It provides an accurate description of the elongation behavior of P pili under stress and supports a hypothesis that the PapA rod shows all three basic stereotypes of elongation/unfolding: elongation of bonds in parallel, the zipper mode of unfolding, and elongation and unfolding of bonds in series. The two first elongation regions are dominated by a cooperative bond opening, in which each bond is influenced by its neighbor, whereas the third region can be described by individual bond opening, in which the bonds open and close randomly. A methodology for a swift extraction of model parameters from force-versus-elongation measurements performed under equilibrium conditions is derived. Entities such as the free energy, the stiffness, the elastic elongation, the opening length of the various bonds, and the number of PapA units in the rod are determined.

INTRODUCTION

Uropathogenic Escherichia coli (UPEC) are bacteria that are implicated in 75–80% of all uncomplicated urinary tract infections as well as in severe pyelonephritis (upper urinary tract and kidney infections). They express fimbrial adhesins, so-called pili, that mediate adhesion and maintain bacteria-host contact during the initial stages of infections. Moreover, P pili are a type of pili that predominantly are expressed by isolates from the upper urinary tract (1,2). Since P pili are expressed by ∼90% of the E. coli strains that cause pyelonephritis, they constitute an important virulence factor (3).

UPEC bacteria are exposed to a variety of mechanical host defenses, in particular urine flow, which expose the bacteria to significant shear forces. Such forces can cause the bacterium-host distance to be dissimilar at different parts of the binding area. Since nonflexible (stiff) parallel bindings will rupture in a serial manner if exposed to forces that give rise to dissimilar elongations (e.g., shear forces) (4), the adhesion mediated by several bindings acting in parallel will be significantly weaker than the sum of the individual bindings (5). However, P pili have evolved into a three-dimensional helix-like structure, the PapA rod, that can be successively and significantly elongated and/or unfolded when exposed to external forces (6–12). The PapA rod is a thin micrometer-long helical rod composed of ∼10³ subunits that are coupled to their nearest neighbors by a β-strand complementation and combined in a right-handed helical arrangement with 3.28 units per turn by layer-to-layer bonds (7,9). The unfolding mechanism of a single P pilus makes it possible for a large number of pili to support tension simultaneously, even in the presence of shear forces (9,10). It has therefore been hypothesized that the flexible structure of P pili makes UPEC bacteria capable of withstanding considerable shear forces, which in turn implies that they can remain attached to the host tissue even in the presence of considerable urine flows. This hypothesis has not yet been verified in vivo. On the other hand, various works have been performed throughout the years aiming for a characterization of P pili with regard to their structure as well as various biomechanical properties.

Until recently, individual P pili had only been characterized with respect to their protein composition and static structure (their size and three-dimensional shape) (6–10). However, because of their specific importance and unique behavior, the mechanical properties of E. coli P pili (both their elongation response to forces (11) and their retraction properties (12)) were recently assessed using force-measuring optical tweezers.

Optical tweezers is a technique that can measure feeble forces in biological systems on a single cell as well as on a single pilus level with a resolution down to sub-pN levels (13). This ability has recently opened new possibilities to study various properties of biological macromolecules, e.g., forces in biological systems and biological motors (14–27), adhesion mechanisms (5,28), and biomechanical properties of pili (11,12,29,30). More specifically regarding pili, the optical tweezers technique has been used by Liang et al. for studies of the binding of E. coli Type 1 pili to specific mannose moieties incorporated into self-assembled monolayers at various concentrations (29) and by Merz et al. for investigations of the retraction of Type IV pili of Neisseria gonorrhoea involved in surface motility (30). Most recently, the elongation and retraction properties of E. coli P pili exposed to external forces have been studied by Jass et al. (11) and Fällman et al. (12).

The study by Jass et al. (11) revealed that the PapA rod of a single P pilus elongates by a passage through a series of regions when exposed to mechanical stress. The first elongation region (for elongations of up to a fraction of its relaxed length (9,11)), referred to as Region I, is characterized by a linear force-versus-elongation response and considered to originate from an elastic stretching of the quaternary structure of the PapA rod (11), which in turn can be attributed to either an increase in the length of the bonds between consecutive turns of the PapA rod (the so-called layer-to-layer bonds, also referred to as the n to n + 3/n + 4 subunit-subunit interactions in the literature (9)), by an elastic elongation of the PapA units themselves, or a combination thereof. The second region (for elongations up to a few times of its relaxed length (9,11), referred to as Region II (11), is characterized by an elongation under constant force and has been attributed to a successive opening of the layer-to-layer bonds, which gives rise to an unfolding of the quaternary structure of the PapA rod (11). Region III, finally, which has an “s” shape, originates from an over-stretching of the linearized PapA rod (11), held together by a β-strand complementation between subsequent PapA units, and includes, as is shown in this work, a phase transition between two discrete conformations of the linearized PapA rod. The previous elongation study (11) also provided information about the stiffness and elasticity modulus for the elastic elongation of P pili and the force required for unfolding of the helix-like PapA rod under steady-state conditions (27 ± 2 pN).

To improve on the understanding of the elongation and unfolding mechanisms of E. coli P pili and advance the characterization of these types of pili, we present in this work a refined model of the elongation and unfolding of the PapA rod of P pili based on an energy landscape model of the bonds that exist between subsequent layers and units in the PapA rod. To provide data to verify the validity of the model, a number of force-versus-elongation experiments using force-measuring optical tweezers have been made.

Pioneering work regarding descriptions of the opening and closure of individual bonds under strain, in terms of an energy landscape model, have been made by Evans et al. (4,31–34). The elongation of biological macromolecules under strain or stress and the influence of entropy and entropic forces in single-molecule measurements have been described by Bustamente et al. (26), Lavery et al. (35), and Rief et al. (36). However, since the PapA rod mainly constitutes a linear macromolecule, folded into a three-dimensional helix-like structure in its ground conformation that can be significantly and successively elongated and unfolded to various degrees when exposed to external forces, we have found it convenient to model its elongation and unfolding properties by a slightly modified version of the one-dimensional “sticky chain” model developed by Jäger (37). This model of the elongation of biological macromolecules under stress is based upon a kinetic description of the opening and closing (unfolding and folding) of the bonds that exist between subsequent layers (or units) in a macromolecule according to a model by Bell (31) and can model both steady-state and dynamic behaviors of both elongation and retraction of biological macromolecules.

A slight complication of our study is, however, that the elongation behavior of a PapA rod consists of all three basic stereotypes of elongation/unfolding (32); elongation of bonds in parallel, the zipper mode of unfolding, and elongation and unfolding of bonds in series. The parallel mode of elongation takes place in region I, in which the PapA rod is fully folded and the applied force is distributed among several bonds per turn (in our case 3.28 bonds per turn). The zipper mode of unfolding takes place in region II, in which the applied force transfers the helical form of the PapA rod to a linearized form by unraveling one bond (the outermost) at a time. The series mode of elongation and unfolding, finally, takes place in region III, in which the PapA rod has been fully linearized, with the remaining bonds (head-to-tail) in series. To provide an adequate description of the elongation properties of the PapA rod, with its rather complex modes of elongation, the sticky chain model has therefore, in this work, been applied to two different modes of operation. The model is used in the so-called cooperative bond-opening mode, in which each bond is affected by the status of its neighboring bonds, for description of the elongation properties in regions I and II. The elongation properties in region III are described by the so-called individual bond-opening mode, in which each bond in the PapA rod experiences the full force and acts independently of its neighbors (wherefore they unfold and refold in a random manner). Although the sticky chain model does not explicitly incorporate entropy (the concept is not mentioned in the original article by Jäger (37)), it includes, as is shown below, in its individual bond-opening mode of operation, the effects of entropy by providing a pseudoelastic elongation (26,35,36).

MATERIALS AND METHODS

Biological system

The biological model system and the culture conditions for maintenance of the bacteria have been described previously (38). In short, a 30-μL sample, consisting of PBS, 9.0 μm hydrophobic beads, and 3.2 μm receptor-coated beads and diluted bacteria, is prepared on a coverslip.

Optical tweezers

The optical tweezers instrumentation used in this work consists of a newly constructed set-up built upon the same principles as those described previously (11,12,38,39), with the following major alterations. The microscope used was an Olympus IX71 inverted microscope modified for focusing laser light by a high numerical objective (100×/1.30 oil immersion, Olympus, Tokyo, Japan). The laser used for trapping was a 10-W continuous Nd:YAG laser (Spectra-Physics, Mountain View, CA) emitting at 1064 nm and run during force measurements with an output power of 1.2 W (measured at the exit port of the laser). This provided a trap with a stiffness of ∼140 pN/μm and a linear measurement range of ±100 pN. The laser used for monitoring the position of the trapped bead, which provides information about the force applied to the biological system, was a 1-mW fiber-coupled intensity-stabilized HeNe laser (Spectra-Physics), emitting at 632.8 nm. Low-frequency noise and drifts that normally limit sensitive force measurements have been significantly reduced by placing the optical tweezers instrumentation on an air-damped optical table in a temperature-stabilized room that is isolated from sound and the ventilation system. Noisy electronic instrumentation, e.g., computers and drivers, have been placed in adjacent rooms. If needed, measurements can be performed without human influence, either by remote control or automated by software.

Measurement procedure

The following measurement procedure was applied. A free-floating bacterium was trapped by the optical tweezers with reduced power and mounted on a large bead, which was immobilized to the coverslip. A small bead was subsequently trapped by the optical tweezers with normal power and brought to a position close to the bacterium. A force measuring calibration procedure, based upon Brownian motion, as described elsewhere (38), was used to calibrate the stiffness of the trap before each new set of measurements.

The small bead and the bacterium were brought in contact and aligned. After alignment, the data acquisition was started and the piezo stage set in motion to separate the bacterium from the small bead. The position-sensitive detector signal (which provides information about the deflection of the bead in the trap and thereby the force in the system) and the output signal from the piezo driver (which provides information about the movement of the coverglass and thereby the distance between the large bead or the bacterium and the trap) were sampled with a data acquisition card (National Instruments, Austin, TX) in an ordinary PC computer with a sampling rate of 170 Hz. The detector signal was filtered by a 30-Hz low-pass filter to avoid aliasing effects. The raw data, which consisted of force-versus-position data for the large bead, was finally converted to force-versus-bead-to-bead distance data in accordance with the procedure given in Jass et al. (11).

A number of bacteria were investigated and a number of measurements were performed on each bacterium/pilus. Each measurement consisted, if possible, of an elongation of the pilus far up into region III, under a constant elongation velocity (thus including a complete unfolding and overstretching of the PapA rod). The movement was then reversed, yielding a retraction of the pilus, so as to allow for a subsequent measurement with the same bacterium/pilus.

A typical set of experimental data is displayed in Fig. 1. The figure shows the elongation of a single P pilus in its three elongation regions as defined above: region I, for forces up to 27 pN; region II, for an elongation at a constant force of ∼27 pN; and region III, for forces above this plateau, up to ∼100 pN, at which the measurement was stopped. If higher forces had been used, the pili would have become detached from the bead at some unspecified force or the bead would have been pulled out from the trap; the rod would, however, not have ruptured, since that would require the breakage of a covalent bond which, in turn, requires a force in the nN range.

FIGURE 1.

A typical force-versus-elongation plot of a single P pilus. The data show three distinct regions, denoted I, II, and III in Jass et al. (11), that originate from an elastic stretching of the PapA rod, a sequential unfolding of the quaternary structure of the rod (which takes place at 27 ± 2 pN (11)), and an over-stretching of the linearized PapA rod, respectively. The x axis refers to the distance between the two beads, but with an arbitrarily chosen zero position.

THEORY

The sticky chain model

As was alluded to above, the sticky chain model is a kinetic model for the elongation of primarily linear but possibly folded biological macromolecules under stress (37). The model is based upon a combination of Hooke's law for the elastic elongation of tandem elements and a rate equation for strain-assisted bond-opening according to Bell (31). It assumes that the rupture of a weak bond immediately leads to a stretching of the macromolecule given by an amount equal to the elongation of the bond, thus neglecting effects of inertia. The model does not take into account any entropic contributions from the elongation of the PapA rod in its native conformation (in its helical form), as the frequently used worm-like chain and freely jointed chain models do (36,40–44). However, this is not considered to be a limitation for the case of P pili, since there is very little bending of the PapA rod in its folded state (the persistence length is almost identical to the contour length (10)), wherefore these entropic contributions are small.

The sticky chain model assumes, in its basic mode of operation, that the energy landscape of the elongation of the macromolecule along the reaction coordinate consists of two states, one that represents a closed and one that represents an open bond. As has been thoroughly discussed in the literature (4,32,33), when an external force, F_ext, is applied to a biological macromolecule, the energy landscape will be tilted, roughly according to the mechanical potential energy 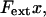where x is the reaction coordinate, in our case given by the elongation distance along the axis of strain. Application of a force to a macromolecule implies that an outer state will be more lowered in energy than an inner state. A transition from an inner to an outer state (i.e., an opening of the bond) can therefore take place whenever the force is “sufficient”.

The kinetics of the opening and closing of a bond, which are described by a rate equation, depend, however, on whether or not the potential governing the bond is affected by the state of the neighboring links. Since the two cases with a zipper (sequential) and series (random) mode of unfolding differ in this respect, two slightly dissimilar rate equations for the strain-assisted bond-opening, leading to cooperative and individual bond-opening, need to be used for modeling the unfolding of PapA rod in regions II and III, respectively.

Nomenclature

Adhering to the basic assumptions and ideas of the sticky chain model as presented by Jäger (37), but adapting the nomenclature to the current case with a biological macromolecule with several consecutive modes of elongation, gives rise to an energy landscape associated with the elongation of the PapA rod along its major axis (in terms of the distance between two PapA units) that consists of three states, labeled A, B, and C, as is shown in Fig. 2. The three states represent combined modes of the two bonds of importance in the system, the layer-to-layer bond and the head-to-tail interaction, as follows: state A, the layer-to-layer bond closed, i.e., with the PapA rod in its helical conformation; state B, the layer-to-layer bond open, thus with the PapA rod in its linearized conformation, and the head-to-tail interaction in its ground state (closed); and state C, the head-to-tail bond in an excited (elongated or open) state, referred to as an overstretched linearized configuration, which is schematically illustrated in Fig. 3.

FIGURE 2.

Schematic energy landscape diagram of the units in the rod along the reaction coordinate (the long axis of the rod) including the three states, A, B, and C, representing the layer-to-layer bond, the (ground) state of the head-to-tail interaction (in the linearized conformation), and an elongated state (an overstretched configuration) of the head-to-tail bond, respectively. The reaction coordinate, denoted x, represents the distance between two PapA units. The uppermost curve represents the energy landscape for a PapA rod not exposed to any force, whereas the other two curves refer to the cases when the PapA rod is exposed to a force that is equal to the unfolding force of the quaternary structure of the PapA rod, F_AB, and the force for which half of the open bonds are in the elongated state, F_BC, respectively. 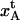represents the elongation of the outermost bond in the helical PapA rod at which the rod unfolds (which is equal to when the A and the B states have the same energy), whereas 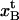corresponds to the elongation of the head-to-tail bond at which the B state will unfold to the C state with the same rate at which the C state bond will refold to the B state (which takes place when the B and the C states have the same energy). 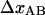and represent the (average) elongation of the layer-to-layer and head-to-tail bonds along the reaction coordinate when they open, respectively. and represent the distances from the minima of states A and B to the subsequent maxima (transition states), respectively.

FIGURE 3.

A two-dimensional illustration of the three states considered in the energy landscape model, with the PapA rod mainly in its helical form in A and in its linearized form in B. The A bonds represent the layer-to-layer bonds, which here, for simplicity, have been schematically represented to mediate a binding between the n and the n + 3 subunits (dashed lines). The B bonds represent the ground state of the head-to-tail interaction in the linearized conformation, whereas the C bonds represent an elongated state (an overstretched configuration) of the head-to-tail bond. As can be seen in A, the quaternary structure of the PapA rod is mediated by several layer-to-layer bonds in the interior of the PapA rod, but only one bond at the end of the rod. The outermost bond therefore experiences a significantly larger force than the inner bonds. This bond will therefore open at a lower force than the inner bonds, which is the main cause for the sequential unfolding of the PapA rod in region II under stress.

Each state is assumed to be harmonic with a potential energy minimum of 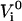and an elasticity constant of k_i according to

(1)

where x_i is the elastic elongation length of the bond relative to the position of the energy minimum of the state i, where i, in turn, takes the value A, B, or C, respectively. This implies, among other things, that the force experienced by a small elastic stretching of a bond a distance x_i, is given by 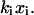We will, for simplicity, assume that

Since there are 3.28 PapA units per turn in the folded state (7,9), the applied force will, in the interior of the helical rod, be distributed among several layer-to-layer bonds. However, as is shown in Fig. 3 A, we will assume that the last (outermost) layer-to-layer bond in the helical structure will experience a significantly larger force (the entire applied force) than the others (the inner bonds), wherefore it will be elongated more than the others. As has been described previously (11), and as is further discussed below, when the pilus has been exposed to a certain well-defined unfolding force, F_AB (referred to as F_uf in Jass et al. (11)), the quaternary structure of the PapA rod will unfold, which is synonymous with the outermost bond opening. Let us denote the elongation of the outermost layer-to-layer bond along the reaction coordinate at which it will open by Since there are 3.28 bonds per turn the applied force is, in the interior of the helical rod, distributed over 3.28 bonds, wherefore the large majority of inner bonds will be exposed to only a fraction of the unfolding force (F_AB/3.28), and thereby elongated only a distance which will be referred to as Moreover, we will denote the elongation of the layer-to-layer bond along the reaction coordinate when the bond opens (which takes place when the applied force has equalized the energy of the A and B states) by 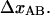As is also shown in Fig. 3, let us furthermore denote the distance between the maximum of the energy barrier between states A and B and the minimum of state A by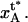

As is discussed below, in contrast to the layer-to-layer bond, not all head-to-tail bonds, represented by state B, will open at the same force (because of entropy). This implies that there will be a distribution of elongations of the head-to-tail bond at which it opens. We will, however, for simplicity, denote the average elongation of a head-to-tail bond at which it opens by and define this as the elongation of the head-to-tail bond under the force at which half of the B-state bonds have been unfolded to the C state, which, in turn, is denoted by F_BC. We will furthermore denote the (average) elongation of the head-to-tail bond along the reaction coordinate when the bond opens by 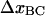and the distance between the maximum of the energy barrier between states B and C and the minimum of state B by 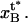Let us finally denote the number of PapA units in the rod that mediate the attachment by N_tot.

Kinetic description of the unfolding and folding of the PapA rod

Since the unfolding of the quaternary structure of the PapA rod (region II) takes place by a sequential unfolding of the outermost bond (in a zipper mode of unfolding), the rate equation for the number of closed layer-to-layer bonds, N_A, can, with the nomenclature used above, be written in a manner that is similar to Eq. 8 in Jager (37), viz. as

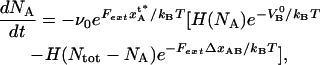(2)

where ν₀ represents an (effective) attempt rate, F_ext is the external force to which the PapA rod is exposed, and 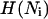is the Heaviside function, which takes a value of unity when its argument is >0 and of zero otherwise.

For the case with opening of the head-to-tail bonds, which takes place in region III and represents bonds in series and thereby the random mode of unfolding, the rate equation for the number of closed head-to-tail bonds, N_B, can be written in a manner similar to Eq. 3 by Jäger (37), viz. as

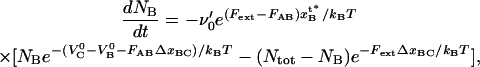(3)

where 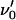again represents an (effective) attempt rate.

The reason why the unfolding of the PapA rod in region II is described by bond-opening and bond-closing rates that are independent of the number of open and closed bond (only given by the Heaviside function) is, as was discussed above, that it is significantly more improbable to open a bond in the middle of the helical structure than one at the end. It is therefore, in reality, only one bond that can open (the last in the helical structure) or close (the first in the linearized structure) for a system with bonds in parallel. This has given this mode of elongation its name; the zipper mode of elongation (45).

In contrast, in region III, in which the bonds are organized in a truly serial manner, each bond acts independently of the others and they can therefore open in a random order. The rate for bond opening in region III is therefore proportional to the number of closed bonds, N_B. This explains why the former of the two expressions above (Eq. 2) is referred to as the cooperative bond-opening model, whereas the latter (Eq. 3) is termed the individual bond-opening model.

Elongation of the PapA rod under stress

For reasons given in the “methodology for evaluation of the model parameters” section below and in the Appendix, it is possible to express the elongation of the PapA rod, in response to the externally applied force, F_ext, in connection with the cooperative bond-opening model, valid for elongation regions I and II (thus, when 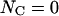), as

(4)

The corresponding expression for the case when the individual bond-opening model is used, valid in region III (thus, when 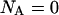), can be written as

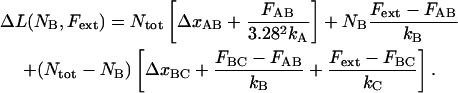(5)

A combination of a rate equation for description of the number of closed and open bonds at a given situation as given above (Eqs. 2 or 3) with the corresponding expression for the elongation (Eqs. 4 or 5) provides thereby a model for the elongation of E. coli P pili under stress.

Loading rate independent response—steady-state solution

The systems above have in general a dynamic response that depends on the loading rate (given by the product of the speed of separation of the large bead and the trap and the stiffness of the probe; for atomic force microscopy (AFM) that of the counterlever and for optical tweezers that of the optical trap). A dynamic response takes place whenever the loading rate is significant in comparison to the product of the applied force and the bond-opening rate (32,34). This is often the case for AFM, for which the loading rates often are substantial (hundreds or thousands of pN/s). For optical tweezers, on the other hand, the loading rates are significantly smaller (often in the low pN/s range) since optical traps have a stiffness that is ∼2 orders of magnitude lower than that of the counterlever used in AFM. In fact, for sufficiently low (and the most common) elongation velocities (in the sub- or low-μm/s range), the loading rates are so small that a given layer-to-layer bond has time to open and close several times before the force has increased noticeably, which corresponds to an elongation under equilibrium conditions, which in turn implies that the opening and closing rates are, at each instance, in balance. The response of the system is then properly described by the steady-state solutions of the rate equations, which are independent of loading rate and thereby independent of the speed at which the PapA rod is unfolded. Since the experiments considered in this work were made under low-loading-rate conditions (∼7 pN/s) and the response of the system was found to be loading-rate-independent (data not shown), we will restrict the analysis in this work to the steady-state solutions of the rate equations.

The steady-state solutions of the kinetic expressions above can be obtained by equalizing the right hand sides of Eqs 2 and 3 with zero. The steady-state solution for the elongation of a biological macromolecule is, for the cooperative bond-opening case, given by Eq. 4 together with

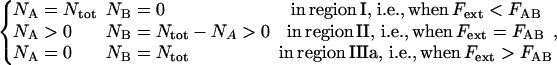(6)

where F_AB is the unfolding force of the outermost bond, given by and where region IIIa represents the first part of region III (in which the head-to-tail bond only is elongated elastically and not unfolded). Unfolding under steady-state conditions takes place when the force has equilibrated the states A and B, however still with a sufficient barrier to state C (which thus has a higher energy than state B). A nonzero steady-state force in region II, i.e., F_AB>0, is in contrast to the opening of a single bond exposed to stress/strain, for which the bond strength depends on the loading rate, approaching zero for infinitely slow elongations (4,31–34). The reason for a nonzero steady-state unfolding/folding force is that the elongation rate is sufficiently slow to provide a balance between the unfolding and folding rates between the states A and B. On the other hand, when the elongation rate is increased above a given level, the forced unfolding rate becomes faster than the spontaneous folding rate, whereby the unfolding enters a dynamic region with a rate-dependent unfolding rate.

The steady-state solution for the elongation of a macromolecule for the individual bond-opening case is, for the individual bond-opening case (thus applicable in region III), for 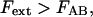given by Eq. 5 together with

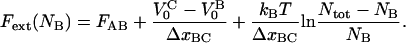(7)

Although this expression is derived from a rate equation for the opening and closing of the head-to-tail bond, it can be shown that it is identical to that which can be derived from considering the force to be given by the derivative of the free energy (expressed as a sum of enthalpy and entropy) with respect to elongation. It also converts, in the absence of the intermediate state and the associated pretension (i.e., with 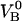= 0 and F_AB = 0), to an expression for elongation/unfolding of a linear macromolecule by a series mode of unfolding of two-level state bonds influenced by entropy.

Model characteristics

As was shown by Jäger (37) and as can be seen above, the two models give rise to dissimilar force-versus-elongation responses, with the most pronounced difference being that the unfolding of the quaternary structure of the PapA rod in region II takes place under a constant force (F_AB), whereas that of the linearized form of the PapA rod takes place under a nonconstant force with a nonlinear force-versus-elongation dependence. A typical response of a system described by the cooperative bond-opening model is shown in Fig. 4 A, whereas the response described by the individual bond-opening model is schematically given in Fig. 4 B. Although not explicitly mentioned in the article by Jäger, the reason for this dissimilarity is due to the different role of entropy in the two cases; there is no contribution from entropy in the cooperative bond-opening model since each bond opens in sequence, whereas the individual bond-opening model, with a random opening and closing of bonds, is strongly affected by entropy.

FIGURE 4.

Typical characteristics of the force-versus-elongation response of the PapA rod according to the sticky chain model under steady state conditions. (A and B) The response from the cooperative and the individual bond-opening models, respectively. The 10 measurable physical entities are indicated: the elongation of the PapA rod in regions I, II, IIIa, and IIIb, denoted by 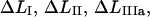and 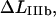respectively; the slope of the force-versus-elongation curve in regions I, IIIa, IIIb, and IIIc, denoted by 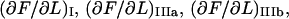and respectively; the force at which the PapA rod unfolds, F_AB; and the force at which there is an equal number of bonds in states B and C under steady-state conditions, F_BC.

As can be seen by a comparison of the typical response of the model system given in Fig. 4 with that of the experimental data presented in Fig. 1 above, the two models have large resemblance with the experimental data from elongation of P pili; Fig. 4 A strongly resembles regions I and II and the first part of region III in Fig. 1, whereas Fig. 4 B bears a striking resemblance to region III in Fig. 1. This shows that the reason for the nonconstant and nonlinear force-versus-elongation response in region III can be attributed to entropy caused by a random bond-opening (and, as will be shown below, can be fully attributed to this), whereas the elongation of the PapA rod in region II under constant force is evidence of the fact that the unfolding of the PapA rod indeed takes place with a sequential opening of the outermost bond (in an entropy-free zipper mode of unfolding).

The question is then how well the sticky chain model can describe the actual elongation and unfolding behavior of a PapA rod from P pili, how large the various physical model entities for a P pili are, and with how much accuracy they can be assessed.

A methodology for evaluation of the model parameters

The model above requires knowledge of 10 model parameters to provide a complete description of the system (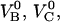 k_A, k_B, k_C, 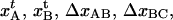and N_tot), of which eight are independent and two can be expressed in terms of others. It is in principle possible to fit the sticky chain model, as given above, with its two formulations for cooperative and individual bond-opening with eight independent model parameters as free parameters, to the experimental data until the fit converges. Although such a general fitting procedure can give rise to a good or bad fit (depending on whether the model used describes the basic physical phenomena that take place sufficiently well and the fitting program is capable of finding a global minimum in the fitting process), it is not always clear that a given fit provides a well-defined value of each parameter. A badly conditioned model or a nonoptimum fitting procedure can provide almost equally good (or bad) fits for a variety of parameter values (one parameter can be traded for others), which thus does not provide adequate information about the physical system and the processes involved.

It is possible, however, in this case, to show that the best fit will produce well-defined values of all 10 model parameters. The reason is that there is an equal number of specific measurable entities (10, of which 8 are independent and two can be expressed in terms of each other) that easily can be identified and individually assessed from an experimental force-versus-elongation curve (four lengths, two force values, and four stiffness values, all properly defined in the Appendix). These 10 entities are indicated in Fig. 4 for clarity. Furthermore, as is illustrated in the Appendix, it is possible to assess, from the measured entities, in an unambiguous manner (i.e., without any fitting), all model parameters that are needed to fully describe the system. The 10 measurable entities (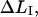 F_AB, etc.) are given in the lefthand sides of the expressions A2–A3, A6–A10, and A12–A15 in the Appendix, which also show their relation to the various model parameters (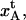 k_A, etc.). By a successive elimination of the model parameters from these expressions it is possible to obtain a unique expression for each of the 10 model parameters, expressed solely in terms of measurable entities. These relations are, for simplicity, collected in Table 1.

TABLE 1.

The 10 model parameters expressed in terms of other model parameters or easily measurable entities

Model parameter	Expressed in other model parameters	Expressed in measurable entities

With the model parameters determined according to the recipe given in Table 1, the model should mimic the actual measurements reasonably well. It is possible and recommended though, if the highest accuracy is needed, to use these model parameters as starting values in a fit of the entire sticky chain model to the measurement data. Not only will such a fit provide the most accurate values of the various model parameters, the goodness of the fit will also indicate whether there are any physical phenomena in the elongation of P pili that are not properly accounted for by the sticky chain model.

RESULTS

A large number of elongation experiments (several hundreds) were performed under the conditions specified in Materials and Methods, above. In general, the data show evidence for both single- and multi-pili attachment. As has been shown in previous works, e.g., Jass et al. (11), a typical set of data shows multi-pili attachments in the beginning of an elongation cycle, with pili detaching sequentially as the elongation increases, resulting in an attachment mediated with fewer and fewer pili, leaving in some cases an attachment mediated by a single pilus at the end of the elongation cycle.

The way a specific measurement was carried out affected the data to a certain extent. For example, a gentle touch of the small bead to the bacterial pili resulted, in general, in the attachment of a small number of pili. However, because these pili did not bind to the bead exceedingly strongly, they generally detached early, often in region I or II or in the first or the middle part of region III, thus preventing a recording of a single-pilus elongation cycle over all three elongation regions. On the other hand, if the small bead was pressed toward the bacterial pili with some (minute) force, the pili were attached more strongly to the small bead, although more pili got attached. This implied that situations in which at least one pilus remained attached to the bead throughout the entire region III often gave rise to a complex multi-pili attachment in the first part of elongation, preventing a clear single-pilus response over all three elongation regions.

As a consequence, among the many hundreds of experiments performed, only a limited number provided a full and unobscured elongation of a single pilus throughout all three elongation regions. Therefore, to provide sufficient data for adequate assessment of the model parameters, data that did not show single-pilus elongation throughout all three regions were also scrutinized. The data curves were separated into four groups: 1), those that show a clear single-pilus elongation response throughout all three elongation regions; 2), those that show a clear single-pilus response in region I and II, but attachment for only a part of region III; 3), those that show multi-pili attachments during the first part of the elongation (obscured data from region I), but a clear single-pilus response for at least the latter part of region II and the entire region III; and 4), those that show either more complicated multi-pili attachments or attachments in which all pili detach before reaching region III.

The data from group 4 were excluded from the analysis. Whereas the curves in group 1 can provide a full set of model parameters for a given pilus, the curves in group 2 provide information about the parameters that are associated with region I ( and k_A), one parameter associated with region II (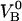), and N_tot, all under the condition that 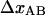is considered known. The curves in group3, finally, provide information about all parameters in region III, as well as N_tot.

Some typical experimental results, taken under low loading rates (i.e., equilibrium conditions), are displayed in Figs. 5 and 6. Fig. 5 shows four consecutive elongations of the same pilus (the second through fifth elongation cycles), all belonging to group 1, whereas Fig. 6 displays data from four different bacteria/pili belonging to group 3.

FIGURE 5.

Force-versus-elongation measurements of four consecutive elongations of the same pilus. The solid lines represent fits to the data according to the model of the PapA rod given by Eqs. 4–7. The fits are within the data points at all instances except for the small peak at the beginning of region II, which is assumed not to originate from the PapA rod, but possibly from the tip of the P pilus. The stochastic variations of the parameter values of the fits are, for multiple measurements of the same pilus, within a few percent.

FIGURE 6.

Force-versus-elongation measurements of pili from four different bacteria, all showing multiple pili attachment for small elongations. The fits are made with fixed values of k_A and taken from measurements belonging to group 1 and 2 data. The fits provide information about the contribution of the last pilus to the multiple pili attachment for small elongations.

For each data curve that was analyzed, the expressions in Table 1, originating from the procedure derived in the Appendix, were first used to produce initial model parameter values. To improve on the accuracy of the determination of the various model parameters, these initial model parameter values were then used as starting values in a fit of the full set of equations, according to Eqs. 4–7 above. The resulting fits are marked with solid lines in the figures. The model parameter values that resulted from the fits agreed in general well with the initial estimates made from the expressions in Table 1.

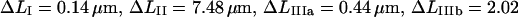
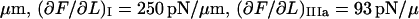
As an example, the data curve displayed in Fig. 5 A provided the following values of the measurable entities: 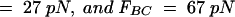. These values produced initial model parameter values from the procedure given in Table 1 of 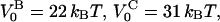k_A = 52 pN/nm, k_B = 210 pN/nm, k_C = 240 pN/nm, and N_tot = 2230. A subsequent fit of the model to the data provided model values of 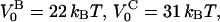k_A = 45 pN/nm, k_B = 140 pN/nm, k_C = 420 pN/nm, and N_tot = 2170, which clearly are in reasonable agreement with the initial values obtained by the procedure outlined in the Appendix. As for this example, the agreement between the model and the measurement data is in general good, and in many cases excellent. This shows that the model encompasses all the basic features that take place in the biological system. (The additional peak clearly shown in the beginning of region II in the curves in Fig. 5 is not predicted by the model for the elongation of the PapA rod given above. The origin of this peak, which appears frequently in some sets of data, but not at all in other sets (as for example can be seen in Fig. 1, in Jass et al. (11), and in Fällman et al. (12)), is not yet fully understood. However, it is plausible that it originates from an elongation of the PapE sequence of the tip of the P Pili.)

The data in Fig. 5 reveal also that the force-measuring system and the biological assay provide a combined system with an exceedingly good reproducibility. The stochastic variation of the data from repeated measurements on the same pilus is in general small and the fits of the model to repeated measurements from one given pilus (such as those presented in Fig. 5) provide values of the various physical model parameters that are consistent within a few percent. This shows, first of all, that a given pilus behaves very reproducibly under repeated elongations. It also shows that the fluctuations originating from the measurement system are significantly smaller than the features measured. This implies, in turn, that it is in general sufficient to analyze only a limited number of data curves from each pilus to get adequate and representative values of the various model parameters for that particular pilus.

The data displayed in Fig. 6 show both evidence of multi-pili response for short elongations and the typical spread in pili response (pili length, etc.) from a set of dissimilar pili/bacteria. As can be seen by a comparison with the plots in Fig. 5, the physical properties of dissimilar pili vary more than the stochastic fluctuations of the physical properties of a given pilus.

A compilation of the mean value of the 10 model parameters, obtained from a number of measurements of various bacteria/pili, e.g., those that are shown in Figs. 5 and 6 but also from other data curves (not shown), are compiled in Table 2. The parameter values were constructed by the following procedure. First, the data curves belonging to group 1 (n = 9) were evaluated, providing values for all model parameters according to the procedure outlined above (using the “swift” methodology described in the Appendix followed by a full fit using the values obtained as starting values), from which an average value of was calculated. The data curves belonging to group 2 (n = 11) were then analyzed. 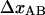For each data curve, N_tot was first estimated from the length of region II, using the value of from the analysis of the group 1 data. With N_tot determined for each curve, k_A and could then be assessed according to the recipe in Table 1. The data curves belonging to group 3 (n = 8) were then analyzed for region III with the model parameters from region I and II (k_A, 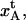and ) considered fixed, taken as the means of the values resulting from the analysis of the data curves in groups 1 and 2. The actual values of the model parameters from regions I and II did not affect the values of the model parameters in region III. Table 2 was finally constructed by taking the mean and standard deviation of all model parameters obtained from all data curves. In the end, the assessment of the model parameters associated with region III was based upon 17 sets of data, whereas k_A, and 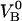were determined from 9, 20, 20, and 28 data curves, respectively.

TABLE 2.

Model parameter values for the elongation of the P pili PapA rod of E. coli under stress obtained from optical tweezers measurements

Model parameter	Value	Model parameter	Value
VB0	23 ± 1 kBT	xAt	0.53 ± 0.2 nm
VC0*	32 kBT ± 2 kBT	xBt	0.23 ± 0.06 nm
kA	61 ± 20 pN/nm	ΔxAB	3.5 ± 0.1 nm
kB	170 ± 40 pN/nm	ΔxBC	0.94 ± 0.05 nm
kC	320 ± 140 pN/nm	Ntot	1430 ± 520

^*This implies that the energy of the head-to-tail bond, given by 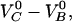is 9 ± 2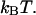

The data evaluation procedure given above and the data in Table 2 also enabled an extraction of the response in regions I and II of the remaining pilus from data curves in which region I and II are affected by multi-pili attachments, i.e., for those belonging to group 3. The fits displayed in Fig. 6 show that the transition from multi-pili to single-pilus response took place when the last pilus was in region II in three of the four panels in Fig. 6 (A, C, and D), whereas it took place when it was in region I in Fig. 6 B.

DISCUSSION

Since it was concluded that the quality of the fits to individual data curves is, in general, very good, and that the stochastic variations of the parameter values from repetitive measurements on one single pilus is small (Fig. 5), it is possible to conclude that the spread in parameter values given in Table 2 mainly has other origins. A closer scrutiny of the data in Table 2 shows that six of the parameter values have significantly larger relative spread than the others. The model parameters with large spread are the stiffness values and the elastic elongations of the bonds, i.e., k_A, k_B, k_C, and 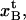and the total number of PapA units, N_tot, which have relative spreads in their values from 24% to 54%, whereas the free energies and the elongations along the reaction coordinate of the bonds when they break, i.e., and have relative spreads of <6%.

In addition to a spread in parameter values from within a population of pili, it is possible that the spread given in Table 2 in parts, and in particular the entities that rely on the measurable entities in region I, i.e., k_A and 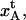also can originate from an elasticity of the bacterium, entropic contributions of the folded PapA rod, and cancellation effects in the data analysis. Although there has been no evidence of any elasticity of the bacterium, if it existed, it would affect the short region I more than the others, whereby 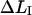and 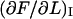could be affected. Moreover, although the PapA rod has a persistence length that is very similar to the contour length (which makes entropic contribution small), it is not impossible that there could still be some minor amounts of entropic contributions that could affect the first part of region I. Some data curves show indeed a small curvature of the first part of region I (although so small that they cannot be seen on the scale at which the data is displayed in Fig. 5). It is therefore, in fact, possible that these two effects can affect the determination of the model parameters that are associated with region I, i.e., k_A and 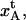and be in part responsible for the large spread in their values.

Furthermore, the conversion of force-versus-position data for the large bead to force-versus-bead-to-bead distance data can lead to errors in the determination of the length and slope of the regions in which the force increases markedly because of cancellation effects (subtraction of one large length (the shift of the position of the small bead in the trap) from another (the movement of the large bead)). The relative error in a model parameter evaluated from such a region becomes presumably larger the shorter the region. This effect, if noticeable, is therefore expected to be most severe in the shorter regions, i.e., again region I but also, to a certain extent, regions IIIa and IIIc, and thereby mostly affecting 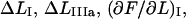and This would imply that the model parameters that depend on these four entities, which are the stiffness values and the elastic elongations of the bonds, i.e., k_A, k_B, k_C, and are expected to be more affected by this phenomenon than the other model parameters.

When it comes to the number of PapA units, N_tot, on the other hand, it should be noted that the determination of this entity from data curves belonging to one given pili could be done with an exceptionally small fluctuation (the average value of N_tot of the curves displayed in Fig. 5 was found to be 2120 ± 30, which corresponds to a stochastic variation of 1.4%). The large spread in the value of N_tot given in Table 2 (1430 ± 520, corresponding to a spread of 36%) only appears when an averaging over a population of dissimilar pili is performed. This is in full agreement with expectations, since the length of pili have previously been found to vary significantly (11) and since it is fully possible that dissimilar fractions of a PapA rod mediate the binding in various experiments (since the attachment of the pilus to the small bead was nonspecific, and not mediated by the adhesion at the tip). This implies, in turn, that the spread in values of N_tot should not be seen as a spread of the total number of PapA units in the rod, but rather as a spread in values of the number of the units mediating the binding in the experiments performed.

Moreover, since it is known that the pitch of the helical structure of the PapA is 2.5 nm (9), a well-defined number of units in the PapA rod provides, in turn, the possibility of estimating the natural length of a pilus with good accuracy. It is, for example, possible to conclude that the natural length of the pilus examined in Fig. 5 A, for which N_tot = 2170, is 1.63 μm.

The model parameter values for the PapA rod obtained in this work (presented in Table 2) can be compared with those of other biological macromolecules. The elastic elongation of the head-to-tail bond (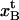) was found to be 0.23 ± 0.06 nm. This is comparable to the bond length reported for L-selectin (∼0.24 nm) (46) and the typical length of a hydrogen bond associated with peptide moieties (∼0.29 nm) (47). The length of the layer-to-layer bond, on the other hand, was found to be significantly longer (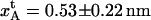). Also this length is comparable to binding lengths found in the literature, e.g., that of the platelet membrane receptor glycoprotein Ib-IX complex to the A1 domain of the von Willebrand factor in the subendothelium matrix in blood vessels, which has been found to range from a fraction of a nanometer to 1.4 nm (48).

The value of the elongation of the layer-to-layer bond along the reaction coordinate when the bond breaks, which was found to be 3.5 ± 0.1 nm, can, together with the bond length of the layer-to-layer bond, 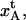provide information about the relative elongation of the PapA rod under unfolding. The relative elongation of the PapA rod is defined as the ratio of the length of the sum of regions I and II and the unstretched length, which is equal to the ratio of 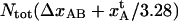and the unstretched length of the PapA rod, which is equal to N_tot2.5/3.28 nm, where the factor of 2.5 nm represents the pitch of the PapA rod and 3.28 represents the number of PapA units per turn (9,10). The data in Table 2 indicate that the relative elongation of the PapA rod is 4.9 ± 0.2. This value corresponds well to previously reported values of 5 by Bullitt and Makowski (9,10) and reasonably well to the value of 7 ± 2 reported by Jass et al. (11).

The slightly higher value of the relative elongation of the PapA rod reported by Jass et al. points out a possible systematic error in the determination of the unstretched length of the PapA rod in that work (11). Since the unstretched length of a pilus could not be irrefutably assessed in that work, it was assumed that it was equal to the distance between the bacterium and the small bead, which could be assessed with good accuracy. This distance is, however, only the minimum possible length of the pilus. If the pilus had originated from any other position on the bacterium, it would have been longer, and the relative elongation would have taken a correspondingly smaller value. The discrepancy of the relative elongations between this work and that of Jass et al. (11) therefore suggests that the assumption made in that work about the natural length of pili was not fully correct, and that they were up to 85% longer than the distance between the bacterium and the small bead.

The reason for the small uncertainty in the value of the relative elongation presented in this work can be attributed to the fact that the elongation of the layer-to-layer bond along the reaction coordinate when it breaks, 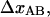could be determined with a relatively small uncertainty (3%). This originated in turn from the fact that the number of units in the PapA rod, N_tot, and thereby the unstretched length of the PapA rod, could be determined with good accuracy.

The free energy of the two bonds (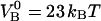 and 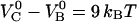) corresponds well to the binding energies of other noncovalent bonds found in biophysical systems. Binding energies of protein-ligand pairs start as low as 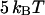and range up to 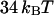for the strong biotin-avidin bond (49), with the titin domain unfolding ranging from 17 to 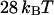(50) and with the biotin-streptavidin bond around 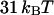(51) in between.

Finally, the value of the elongation of the head-to-tail bond along the reaction coordinate when it opens, which was only 0.94 ± 0.05 nm, was found to be significantly smaller than that of the layer-to-layer bond, i.e., (only 27% of ). This discrepancy is in agreement with the differences in stiffness and free energy of the two bonds; the stiffness of the head-to-tail bond (170 pN/nm) was found to be ∼3 times larger than that of the layer-to-layer bond (61 pN/nm), whereas the free energy of the unfolding of the head-to-tail bond, 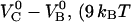) was found to be 39% of that of the layer-to-layer bond, ). Both these effects advocate that 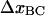should be smaller than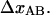

SUMMARY AND CONCLUSIONS

We have presented a sticky chain model that successfully has been used to model the elongation of the P pili PapA rod from E. coli under stress under steady-state conditions. The model is developed both for a cooperative bond-opening mode, with an opening and closing of bonds in a sequential order, used to describe the elongation of the PapA rod in regions I and II, and for an individual bond-opening mode, with a random opening and closing of bonds, used to describe the elongation in region III. The model describes, as a whole, the elongation of a PapA rod under stress over all elongation regions under steady-state conditions and the predictions are in good agreement with experimental data. A procedure for a swift evaluation of all 10 model parameters associated with the energy landscape of the PapA unit interactions from particular features in the experimental data (given in the Appendix) has been developed. The model parameter values obtained by the fast evaluation procedure differ in most cases from those obtained from a full fit by <10%. If the highest accuracy is needed, the parameter values that result from the fast evaluation procedure can therefore be as initial values for a fit of the sticky-chain model to the data under equilibrium conditions. Table 2 summarizes the model parameter values that were obtained from fits of the full model to data from 15 sets of measurements in terms of a mean value, with an associated uncertainty given as one standard deviation. Although the model parameters that originate from measurement data from region I possibly could be affected by systematic errors, the others are assumed to represent well the true values of the model system. The model parameter values obtained (both the lengths and the energies of the layer-to-layer bond as well as the head-to-tail bond) were found to be in good agreement with those of other macromolecules. The model parameters whose values vary due to natural variations in environmental conditions such as pH and salinity, the elongation of P Pili under dynamic conditions, as well as the origin of the small peak at the beginning of region II in Fig. 5 are subjects for future studies.

APPENDIX: A METHODOLOGY FOR EVALUATION OF THE MODEL PARAMETERS FROM MEASUREMENT DATA

There are 10 entities that can easily be defined from a measured force-versus-elongation curve (four lengths, two force values, and four stiffness values). By use of Eqs 1–7 above, each measurable entity can be expressed in terms of a combination of model parameters as follows.

Region I

Since there are 3.28 PapA units per turn in the folded state (7,9,52) and the number of PapA units in the rod is denoted by N_tot, the number of turns (layers) in the PapA rod is N_tot/3.28. This implies that an elongation of an inner layer-to-layer bond, which mediates the binding between two consecutive layers a distance 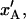will give rise to an elongation of the PapA rod in region I, 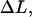of 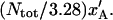Moreover, since an externally applied force of F_ext will be evenly distributed among 3.28 bonds in the interior of the helical rod, the force to which an inner layer-to-layer bond is exposed is given by F_ext/3.28. This force will, in turn, elongate an inner layer-to-layer bond an amount 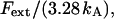where k_A is the stiffness of the layer-to-layer bond, as defined by Eq. 1. This implies, finally, that the relation between the applied force, F_ext, and the measured elongation of the PapA rod in region I, can be written as

(A1)

This implies, in turn, that the apparent stiffness in region I, defined as 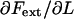and denoted by 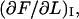is given by

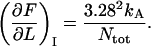(A2)

Since the unfolding of the quaternary structure takes place at a constant force, denoted by F_AB, this implies that the length of region I, 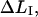can be written in either of the forms

(A3)

The elongation of an inner layer-to-layer bond, just before unfolding of the quaternary structure of the PapA rod, 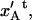can therefore, from the expression above, be written in either of the forms

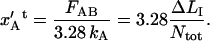(A4)

This implies that the elongation of the outermost layer-to-layer bond, before unfolding, 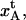becomes

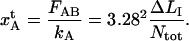(A5)

Region II

The measured elongation in region II, denoted by 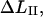is related to the elongation of the layer-to-layer bond along the reaction coordinate when the bond opens, by

(A6)

It can moreover be concluded, from the sticky chain model or from an energy conservation argumentation, that the unfolding force in region II under steady-state conditions, F_AB, can (by equalizing the unfolding and refolding rates in Eq. 2 or by equalizing the area under the curve in region II, 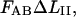to the increase in energy of the molecule, 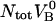) be written as

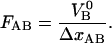(A7)

Region III

Since region III is characterized by a linearized PapA rod, the corresponding expression for the measured stiffness in the first linear part of region III, which is not significantly affected by any entropic softening and is denoted by “IIIa” for simplicity, can be written as

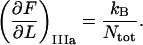(A8)

The expression for the measured elongation in region IIIa, denoted by 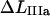and defined as the elongation of the PapA rod in state B that is needed to create the force at which the energy minima of states B and C are equal, F_BC (which also is the force at which half of the bonds in state B have been unfolded to the C state), as is indicated in Fig. 2, is related to the average elongation at which a bond in state B opens, i.e., 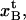according to

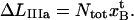(A9)

Since 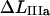also can be expressed as

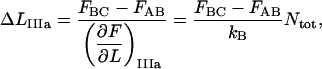(A10)

we find that 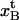can be expressed as

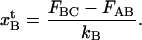(A11)

The corresponding expression for the apparent elongation in region IIIb, defined as shown in Fig. 2 and denoted by 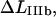is related to the elongation of the head-to-tail bond when the bond opens, 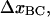in a similar manner, i.e., as

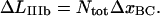(A12)

Moreover, the force at the center part of region III (defined as the position at which half of the bonds have been elongated, which is equal to the position at which the slope of the force-versus-elongation curve has a minimum), will be denoted by F_BC. By equalizing the unfolding and refolding rates in Eq. 4, one finds that F_BC can be expressed as

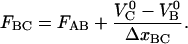(A13)

It can furthermore be shown (by noting that = 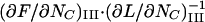and using Eqs 7 and 5) that the slope of the force-versus-elongation curve at this position, denoted by can be expressed as

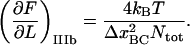(A14)

Finally, the apparent stiffness in the last linear part of region III, denoted by IIIc, can be written as

(A15)

By a successive elimination of the model parameters in the expressions above, we end up with a unique set of expressions for each of the 10 model parameters, expressed solely in terms of measurable entities. For example, the expression for 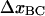can be obtained from Eq. A14 by eliminating N_tot by use of Eq. A12. These relations are, for simplicity, collected in Table 1.