Weak Force Stalls Protrusion at the Leading Edge of the Lamellipodium

Abstract

Protrusion, the first step of cell migration, is driven by actin polymerization coupled to adhesion at the cell's leading edge. Polymerization and adhesive forces have been estimated, but the net protrusion force has not been measured accurately. We arrest the leading edge of a moving fish keratocyte with a hydrodynamic load generated by a fluid flow from a micropipette. The flow arrests protrusion locally as the cell approaches the pipette, causing an arc-shaped indentation and upward folding of the leading edge. The effect of the flow is reversible upon pipette removal and dependent on the flow direction, suggesting that it is a direct effect of the external force rather than a regulated cellular response. Modeling of the fluid flow gives a surprisingly low value for the arresting force of just a few piconewtons per micrometer. Enhanced phase contrast, fluorescence, and interference reflection microscopy suggest that the flow does not abolish actin polymerization and does not disrupt the adhesions formed before the arrest but rather interferes with weak nascent adhesions at the very front of the cell. We conclude that a weak external force is sufficient to reorient the growing actin network at the leading edge and to stall the protrusion.

INTRODUCTION

Crawling motion of animal cells requires three distinct processes: protrusion at the front; graded adhesion, so that there is a firm attachment to the substrate at the leading edge and detachment at the rear; and forward translocation of the cell body (1). The common protrusive appendage characteristic of rapidly migrating cells is the lamellipodium—a broad, flat sheet-like structure, tens of microns in width, and 0.1–0.2 μm thick (2). The lamellipodium consists of a branched polarized network of actin filaments enveloped by the cell membrane. Protrusion relies on a treadmilling of the actin filament array, such that new filaments are polymerized at the lamellipodium's leading edge, whereas old filaments disassemble throughout the lamellipodium (reviewed in Pollard and Borisy (3)).

To overcome the resistance from the external environment and from the cell's own membrane and adhesions, the cell must generate mechanical forces to power its locomotion. In most crawling cells, the force of protrusion is generated locally at the lamellipodium leading edge (4). The physical mechanism of the protrusion force generation is believed to be an elastic polymerization ratchet of growing actin filaments; other mechanisms such as swelling of actin gel and specialized molecular motors are less likely in thin lamellipodium protrusions (reviewed in Mogilner and Oster (5)). To push the cell membrane forward, growing actin filaments near the leading edge should be attached to the substrate through complex and dynamic adhesions that contain transmembrane integrin receptors and a host of other cross-linking and signaling proteins (6). These adhesions are also necessary to pull the cell body forward, which is thought to be driven by myosin-powered mechanisms (7), e.g., contraction of the actin network weakened by disassembly at the rear of the lamellipodium (8).

Polymerization and adhesive forces have been previously estimated. Polymerization ratchet models predict that elongation of a single actin filament generates a force of a few piconewtons (9,10). Considering that there are hundreds of filaments per micron of the leading edge (2), the growing actin network can generate protrusive force in the range of nanonewton per micron. (Other possible force-generating mechanisms are likely to result in similar force magnitudes (5).) This protrusion force is sufficient to overcome the resistance of hundreds of piconewtons per micron required to bend the cell membrane and to break attachments between the actin cortex and the cell membrane (11–13).

Measurements of the protrusive force at the leading edge are difficult to interpret, because transient changes of cell shapes and movements accompany the force application (14). An approximate experimental estimate from deflection of a lightly attached glass microneedle provides the value of a few nanonewtons force stalling the cell (15) in semiquantitative agreement with the theory. Actin networks in vitro generate a protrusive force of the order of a few nanonewton per square micron of the surface they push (16). Without ultrastructural data, this result cannot be extrapolated to the cell leading edge, but a crude estimate of the filament density suggests that the protrusive forces of the in vitro and lamellipodium actin networks are similar. Also consistent with these estimates is the observation that forces in the range of nanonewtons per square micron applied to magnetic beads at the cell surface can either induce or inhibit the cell protrusions (17). Curiously, force of a few piconewtons per micron slows down forward movement of the bead attached to the leading edge of the cell (18), though the relevance of this experiment to the protrusive force generation is unclear.

The adhesions near the cell's leading edge constitute a “slippery clutch” (19) that is able to transduce some of the polymerization force into the forward protrusion, whereas the rest of it powers the retrograde flow of the actin network. Indeed, a single integrin bond can withstand 10–30 pN (20,21). There are hundreds of integrins per square micron of the adhesion, which makes it firm enough to absorb forces of the order of a few nanonewtons per square micron of the substrate. In fact, forces of this magnitude, applied to the substrate through adhesions and generated by myosin-powered contraction and/or actin polymerization, were measured (22–26).

In this study, we attempt to estimate the protrusive force by arresting the leading edge of the lamellipodium of a moving cell. To determine this force, an experimental system is needed which is characterized by a consistent and predictable behavior and which always exhibits protrusion in the absence of the external force. Fish epidermal keratocytes, with their fast and persistent locomotion (10–20 μm/min), persistent polarization, and simple and stable shape, represent an excellent model system (27,28). Free locomoting keratocytes have a characteristic fan-like shape with large lamellipodium. They move in a direction perpendicular to the long axis of the cell, and the leading edge protrusion occurs continuously and at the same rate as the translocation of the cell body, resulting in remarkable conservation of the cell's shape.

To estimate the protrusive force, we arrest the leading edge of a moving fish keratocyte by applying a fluid flow from a micropipette. The flow arrests the protrusion locally and reversibly as the cell approaches the pipette, causing an arc-shaped indentation and upward folding of the leading edge. Surprisingly, the arresting force amounts to just a few piconewtons per micrometer. Furthermore, we establish that the flow neither stops actin polymerization nor disrupts the adhesions formed before the arrest, but rather interferes with the adhesion at the very tip of the lamellipodium. We conclude that weak nascent adhesion at the very tip of the lamellipodium, and not the actin filament elongation, is the limiting factor of the protrusion mechanics.

MATERIALS AND METHODS

Cell culture

Fish epidermal keratocytes from scales of black tetra fish were cultured in Dulbecco's modified Eagle's medium (DMEM) supplemented with 10% fetal bovine serum and antibiotics, as described previously (29). Swiss 3T3 fibroblasts were cultured in DMEM with 10% fetal bovine serum and antibiotics.

Hydrodynamic force generation

The leading edge of the lamellipodium was stopped by application of a hydrodynamic load generated by a stream of culture medium flowing through a micropipette. Micropipettes from 1.0 mm outer diameter × 0.78 mm internal diameter borosilicate glass capillaries were pulled with the P-97 Brown-Flaming Micropipette Puller (Sutter Instrument, Novato, CA) to obtain a 5μm internal diameter of the opening tip. To maintain a controlled nanoliter flow out of the pipette, a femtojet (Eppendorf, Schönenbuch, Switzerland) was used as a pressure source. Injection pressure was set at 0.4 PSI (PSI: pounds per square inch, 1 PSI = 68.97 hPa), and the duration of its application was controlled by experimenter.

The tip of the micropipette was set 2 μm from the substrate to avoid a clogged pipette and flow irregularity. As flow almost parallel to the substrate was required, the pipette was placed such that the stream hit the surface first and then flowed almost parallel to the substrate. As the angle between the pipette and the horizontal was fixed at 45° for every experiment, the distance between the tip of the pipette and the leading edge of the cell must be at least 2 μm. This condition has always been met (n = 35).

Fluorescence staining

Rapid fixation of the cells during the arrest of protrusion was performed by pouring 1 ml of fixative solution into the open petri dish on the microscope stage as described (28).

For β1-integrin immunostaining (n = 4), cold fixative solution containing 2.5% glutaraldhehyde and 0.025% Triton X-100 in culture medium was added for 40 s (30). Cells were then washed three times in phosphate-buffered saline (PBS) (1 min each) and treated with sodium borohydride (2 mg/ml) two times, each for 10 min, and immunolabeled with rabbit anti-integrin β-1 polyclonal antibody (Chemicon International, Temecula, CA).

Fixation and labeling of F-actin with tetramethylrhodamine isiothiocyanate (TRITC)-phalloidin (n = 6) was performed as described (29). To compare the F-actin content in the arrested part of the lamellipodium to that of the neighboring protruding regions, the fluorescence intensity was measured in four equal square regions, which were placed at the same position along the axis of cell migration but at different lateral positions along the leading edge. Two regions were placed over the arrested part of the edge, and the other two over the nonaffected regions at both sides of the arrested part immediately adjacent to it. The average fluorescence intensity of the two squares in the arrested part was then compared to the average intensity of the two adjacent squares in the nonaffected part of the edge.

Phase contrast, fluorescence, and interference reflection microscopy

A Nikon (Tokyo, Japan) Eclipse TE300 inverted microscope was used for enhanced phase contrast (n = 15), epifluorescence, and interference reflection microscopy (IRM) (n = 10) with Nikon Plan 100×, 60×, and 40× phase objectives. Data were acquired with a Micromax PB1300 and a Micromax 512FT cooled charge-coupled device cameras (Roper Scientific, Trenton, NJ) controlled by Metamorph software (Universal Imaging, West Chester, PA).

Flow velocity measurement

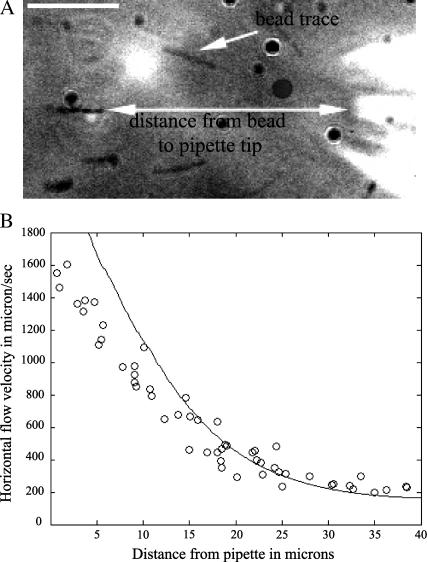
Carboxylate microspheres with a diameter of 0.45 μm (Polysciences, Warrington, PA) were mixed with culture medium and ejected from the micropipette. Their trajectories were recorded alternatively at the focal plane of the pipette tip and 1 μm from the substrate using a piezoelectric translator (Physik Instrumente, Waldbarn, Germany) to position the objective lens. The flow velocity was calculated by measuring the lengths of the bead traces and dividing it by the exposure time (10 ms). The velocity was measured at different distances from the pipette tip. To determine more precisely the dependence of the flow velocity on the vertical distance, the tip of the pipette was positioned 6 μm from the substrate and the trajectories were recorded at different heights from the substrate.

Flow velocity correction and error analysis

The length of the microspheres' traces near the pipette tip is a few microns long. This causes a significant error if the velocity is calculated by dividing the trace length by the exposure time, because the measurements show that the velocity field changes (decreases) rapidly within a few microns from the pipette tip. This causes underestimation of the velocity magnitude, because the value of the velocity assigned to a point in space is in fact an integral of the decreasing velocity field. This error is systematic, and we correct it using the following mathematical procedure. Let T be the exposure time, let x be the horizontal distance from the pipette tip, and let V(x) be the horizontal component of the flow velocity measured as a function of x. Let v(x) be the actual, corrected horizontal component of the flow velocity. Then, if the trace starts at x in space, it ends at (x + TV(x)). The microsphere actually travels between s and s + ds in space within ds/v(s) seconds, so the total time of the trace is

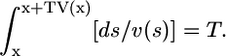We can use this integral equation to compute the actual velocity field v(x) knowing the measured velocity field V(x). We implement this correction as follows. After collecting data, we fit it with a cubic polynomial using a basic MATLAB (The MathWorks, Natick, MA) fitting tool. We then solve the integral equation numerically on the interval from 0 to 40 μm using the collocation method (31), find the difference between this solution and the polynomial fit to the data, and add the difference to the measured values of the velocity. (Such corrected data is plotted in Fig. 6 B.)

FIGURE 6.

Estimation of the flow velocity and comparison with computed flow field. (A) The length of a bead trace divided by the exposure time gives the horizontal component of the flow speed. Bar, 10 μm. (B) Circles show the data for the horizontal component of the flow velocity measured at 2 μm from the substrate as a function of the horizontal distance from the pipette tip. The data represent the measurements corrected for systematic errors as described in Materials and Methods. The curve is the computed corresponding velocity distribution obtained from the numerical simulations of the Navier-Stokes equation. The discrepancy between theoretical and experimental data at small distances (0–10 μm) is due to the systematic errors described in Materials and Methods.

Theoretical simulations of the flow

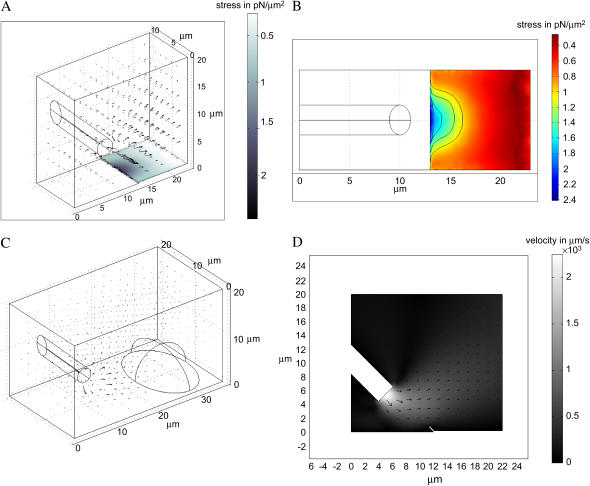
To estimate the arresting forces at the cell leading edge, we developed a three-dimensional (3D) model of stationary flow from the pipette. In the model, we solve the Navier-Stokes equation (32) for incompressible flow of a viscous fluid. To nondimensionalize the equation, we use the pipette diameter as the length scale and the maximal measured flow speed as the velocity scale and then use the density and viscosity of water to scale the pressure and forces. The Reynolds number in the simulations is of the order of unity for experimentally observed flow velocity magnitudes. We solve the equation numerically with the help of the Finite Element method using the Stationary Incompressible Flow Model implemented in Femlab (Femlab Model Library by COMSOL AB; the model geometry is illustrated in Fig. 5, A and C). The flow is simulated in the parallelepiped excluding the volume of the part of the cylinder inside the parallelepiped representing the pipette. The size of the parallelepiped is of the order of ten(s) of microns; we controlled the errors by repeating the simulations in larger volumes and finding that the numerical error at distances greater than a few microns from the pipette tip is <10%. We simulate the flow using the following boundary conditions: no slip at the bottom surface of the parallelepiped and sides of the pipette cylinder, neutral boundary conditions at the sides and top of the parallelepiped, and constant velocity at the base of the cylinder directed along its axis representing the outflux of the fluid from the pipette.

FIGURE 5.

3D finite element simulation of the stationary flow from the pipette. (A) The parallelepiped within which the flow was computed is shown. The computed velocity field is illustrated with the arrows. The flow impinges on the lamellipodium step. The gray scale on the lamellipodium surface illustrates the computed shear stress. (B) The computed (color-coded) shear stress on the lamellipodium surface—view from above. A few stress level curves (on which the stress is constant) are shown. (C) The computed flow impinges on the cell body represented by the half-ellipsoid. (D) 2D simulation of the flow impinging on the lifted lamellipodium tip. The gray scale shows the velocity magnitude.

First, we added a “step” to the bottom surface of the parallelepiped (height 0.2 μm) representing a thin lamellipodium (see Fig. 5 A). We varied the rate of the fluid outflux until we found the best numerical fit to the corrected experimental data (see above) for the distribution of the horizontal component of the fluid velocity along the straight horizontal line from the pipette tip directed oppositely to the cell movement velocity. We fitted the data on the interval between 10 and 40 μm for the following reason. The computed magnitude of the vertical component of the fluid velocity is >100 μm/s at distances from the pipette tip <10 μm. At such speeds, microspheres move >100 μm/s × 0.01 s = 1 μm over the exposure time, which is more than the height of the confocal plane, so the microspheres could go out of focus faster than the exposure time. This leads to underestimation of the fluid velocity at distances <10 μm (which is seen in Fig. 6 B). After the fluid flow is computed, we find numerically the pressure at the front of the lamellipodium step and the shear stress on the surface of the lamellipodium step. As a control, after fitting the horizontal distribution of the flow velocity, we also computed the vertical distribution of the velocity in the same geometry as the corresponding experimental conditions (above) and compared the data with the theoretical values. The corresponding theoretical and experimental data match well.

Second, to estimate the force on the cell body, we exclude from the parallelepiped the volume of the half of the ellipsoid representing the cell body (see Fig. 5 C). The ellipsoid is 18 μm × 12 μm × 12 μm; the size of the parallelepiped is increased accordingly. We use no slip boundary conditions on its surface. In this case, we do not introduce the lamellipodium step, because its influence on the flow pattern on the scale on tens of microns is negligible. After the fluid flow is computed, we find numerically the pressure and shear stress at the surface of the half-ellipsoid.

Finally, to find out if the arresting force on the lifted lamellipodium tip differs significantly from the force on the flat tip, we solve the two-dimensional (2D) flow problem using the same software and methods (see Fig. 5 D). In this simulation, we lift the front 1 μm tip of the lamellipodium step 45°. The boundary conditions at the sides of the domain (shown in Fig. 5 D) are the same as those in the 3D problem. After the fluid flow is computed, we find numerically the pressure and shear stress at the surface of the lifted tip.

RESULTS

Hydrodynamic load induces local and reversible arrest of the leading edge

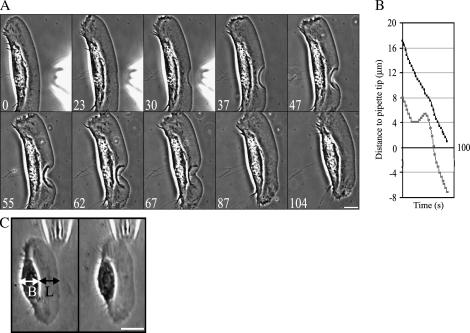
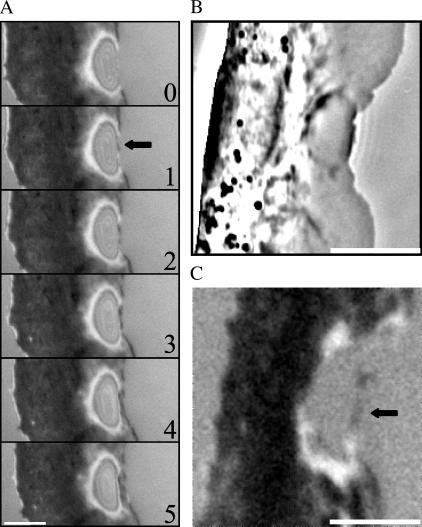
Fluid flow from micropipette was used previously to create a mechanical stimulus inducing a transition from the stationary to the locomoting state of keratocytes fragments (8). We used a similar approach to produce the opposite effect: we attempted to stall the cell by applying a fluid flow to the center of the leading edge of steadily motile cells (fish epidermal keratocytes) in the direction opposite to cell motion (Fig. 1 A, and Supplementary Movie 1). We observed that as the cell approached the tip of the micropipette, the protrusion became locally arrested, resulting in an arc-shaped indentation of the leading edge, as appeared in the phase contrast sequences, by detaching and backward folding of the thin lamellipodium rim of the stalled part of the edge. The protrusion stopped in an abrupt manner at a horizontal distance from the pipette tip that varied in different experiments between 3 and 6 microns (over 30 cells were locally arrested in this manner, and the effect was highly reproducible). Upon pipette removal, the indentation began to “heal” steadily, and the leading edge recovered its initial shape within ∼1 min (Fig. 1 A and Supplementary Movie 1).

FIGURE 1.

Reversible arrest of the leading edge by a hydrodynamic load. (A) (0–30) As the cell approaches the pipette tip, the protrusion becomes locally arrested by the flow, resulting in the arc-shaped indentation of the leading edge. (37–104) The leading edge recovers its initial shape when the pipette is removed. (B) Traces of the position of the leading edge and the front boundary of the cell body. Whereas the leading edge of the cell is arrested by the flow and then recovers after the pipette removal, the cell body translocation is unaffected. (C) Flow parallel to the leading edge neither stops the protrusion nor affects cell motility in general. L stands for the lamellipodium and B for the cell body. Bar, 10 μm; time in seconds.

The fluid flow did not have any effect on the cell body (Fig. 1 B) or on the lateral sides of the lamellipodium (Fig. 1 A and Supplementary Movie 1), which continued to move in the presence of the stream at the same rate as in the absence of the flow. Importantly, the effect of the flow was directional: when we applied the flow in the direction parallel to the leading edge, this had no effect on the leading edge protrusion (Fig. 1 C). Also, neither the forward translocation of the cell body nor the cell shape was affected by this flow.

Fish keratocytes, due to their persistent and regular motion, presented a favorable model system to study the effect of the flow force on local protrusion. Nevertheless, to elucidate if the effect of the flow was cell-type specific, we also applied pipette flow to spreading 3T3 fibroblasts. As these cells were mostly stationary, the effect of the flow was tested by approaching the cell with the pipette tip, rather than waiting for the cell to approach the pipette. When the pipette tip was within several micrometers from the cell edge, a local concave indentation of the edge similar to that of the keratocyte lamellipodium was observed at the site closest to the pipette (Supplementary Movie 3). This experiment indicated that the flow effect was not specific to keratocytes but rather common to various cell types.

Effect of the flow on actin polymerization and substrate adhesion

Cell protrusion is driven by actin polymerization coupled to substrate adhesion; therefore, possible effects of the flow include abolishing actin polymerization and the disruption of lamellipodium adhesion. The third possibility is that the flow could make the adhesions weaker, which would turn actin polymerization coupled with contraction at the base of the lamellipodium into a retrograde flow of the lamellipodial network. The following experiments showed that neither of these processes took place.

In keratocyte lamellipodium, it has been shown that the actin filaments formed a network exhibiting a fine crisscross pattern with the highest density at the leading edge and a gradual decrease toward the nucleus (29,33). Fixing the cell at the moment of the protrusion arrest and staining it with TRITC-phalloidin showed similar organization of the actin in the lamellipodium (Fig. 2 A), so the protrusion arrest was not caused by global damage to the actin network. The intensity of the fluorescence was highest at the site of arrest at the leading edge (Fig. 2 A), which was likely, partially, due to the increased optical path through the lifted part of the edge. To compare the amount of F-actin assembled in the arrested part of the edge to that of the neighboring protruding parts, we measured fluorescence intensity in the cells fixed at the time of protrusion arrest and stained with fluorescent phalloidin (see Materials and Methods). The average fluorescence intensity in the arrested part was equal to 92% ± 23% (standard deviation, n = 6) of the average intensity of the adjacent nonaffected regions of the same area, suggesting that the actin polymerization was not abolished by the flow, but rather redirected to form an upward ruffle-like extension instead of forward protrusion.

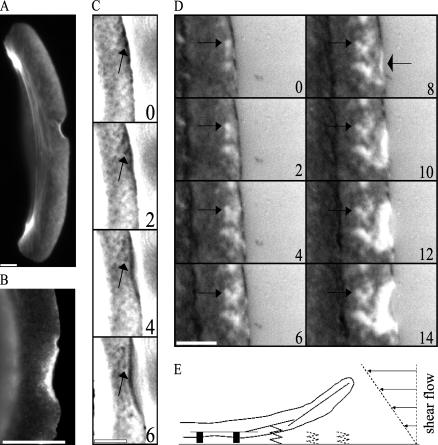
FIGURE 2.

Effect of the flow on actin polymerization and substrate adhesion. (A) The flow does not affect actin polymerization: TRITC-phalloidin staining of the keratocyte fixed at the moment of the protrusion arrest shows F-actin accumulation at the site of the arrest and a fine crisscross pattern of the F-actin network with the highest density at the leading edge and a gradual decrease toward the nucleus. (B) Integrin β-1 immunostaining of the keratocyte fixed at the moment of the protrusion arrest shows that integrin β-1 is enriched in the lifted part of the edge as well as in a narrow rim along the intact leading edge. (C) F-actin network assembled before the arrest is not displaced with respect to the substrate: enhanced phase contrast microscopy of the lamellipodium reveals distinct features of the F-actin network (arrows) remaining nearly stationary with respect to the substrate. (D) IRM demonstrates that the adhesion pattern formed before the arrest (arrows on the left) is not affected by the flow; however, the flow interferes with the nascent adhesions at the very tip of the lamellipodium, which lifts up (narrow bright zone indicated by the arrow on the right). (E) Model: hydrodynamic load interferes with the weak nascent adhesions and reorients branching and elongation of the leading edge actin filaments away from the substrate. Bar, 5 μm; time in seconds.

Neither did the flow generate the retrograde movement of the lamellipodium network, as was revealed by enhanced phase contrast microscopy of the lamellipodium. This microscopy shows variation of the actin density resulting in the crisscross pattern, so time-lapse observation of the protrusion before and during its arrest allows visualizing and following distinct features of the actin network. We observed that such features remained nearly stationary with respect to the substratum (Fig. 2 C). This experiment suggests that the retrograde flow of the F-actin network in the lamellipodium is not accelerated by the applied hydrodynamic force. (The keratocytes always exhibit a very slow, ∼20–30 nm/s, retrograde actin flow at the front (34).)

Finally, we used IRM to study the closeness of the contact between the cell and the substrate (35). Previously, a combined IRM and total internal reflection fluorescence microscopy study (30) established that varying gray shades in IRM faithfully represented variations in adhesion closeness in keratocyte lamellipodia. It was demonstrated that keratocytes have a rim of close contacts at the leading edge (30). This region is thought to correspond to the site where nascent cell-substrate adhesions are formed and where a distinct pattern of close contacts is generated (30). In agreement with Lee and Jacobson (30), we observed in time-lapse images the dark zone at the very tip of the leading edge (Fig. 2 D and Supplementary Movie 2) corresponding to the region of the close contacts. We also observed that the adhesion pattern formed before the protrusion arrest did not change by the application of the flow (Fig. 2 D and Supplementary Movie 2), so the flow does not disrupt the preformed adhesions. However, under the influence of the flow, the narrow (a few tenths of a micron wide) rim at the very tip of the lamellipodium became bright, suggesting that the flow interfered with the formation of the nascent adhesions under the stalled part of the leading edge. Subsequently, the bright area at the arrested part of the edge increased in size, suggesting detachment from the substrate and thus reinforcing the results of phase contrast and fluorescence microscopy showing that the affected part of the edge formed a kind of upward ruffle. The rim of the close adhesions at the tip of the lamellipodium was previously shown to contain integrin β-1 (30). To determine if the flow interfered with the localization of integrin β-1, we fixed and stained stalled cells with the antibody to this adhesion component. The lifted part of the leading edge turned out positive for integrin β-1 (Fig. 2 B), suggesting that the flow interfered with the mechanical integrity rather than with the chemical composition of the adhesions.

Leading edge recovery

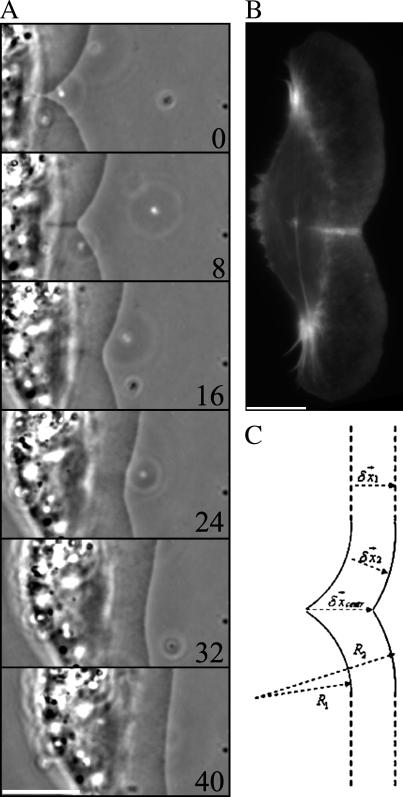
We established that the flow interfered with the nascent adhesions at the very tip of the leading edge and that the effect of the flow was rapidly reversible upon the pipette's removal. Next, we investigated the pathway of the leading edge recovery. IRM suggested that after interfering with the adhesions, the flow “blew up” part of the leading edge like a bubble (Fig. 3 A and Supplementary Movie 2). Upon the removal of the pipette, the adhesions were first reestablished at a small region at the tip of the edge, at the forward side of the bubble (Fig. 3 A and Supplementary Movie 2). Then, within seconds, the narrow adhesive zone was established “zippering together” the remaining adherent parts of the leading edge at the two sides of the bubble and thus resurrecting the continuous adherent leading edge (Fig. 3, A–C). The bubble of the lifted lamellipodium was left behind as protrusion resumed.

FIGURE 3.

Recovery of the substrate adhesion after the arrest of the leading edge. (A) IRM demonstrates that the adhesion of the leading edge is first reestablished at a small region at the tip of the edge (arrow) and then zips in from both sides, generating a continuous adhesion zone. Simultaneous phase contrast (B) and IRM (C) imaging confirms that adhesion is first reestablished at the very tip of the leading edge. Bar, 5 μm; time in seconds.

After the readhesion, within ∼1 min, the initial shape of the leading edge recovered. The kinetics of the shape recovery (Fig. 4 A) gave an impression that an accelerated protrusion at the site of the arrest was responsible for stabilizing the leading edge. However, simple geometric modeling demonstrated that the recovery of the initial shape of the cell edge could be explained by the normal edge extension as postulated in the graded radial extension (GRE) model (36). According to this model, the advancing lamellipodium can be described geometrically by attributing the normal velocity of protrusion to every point of the leading edge. The rate of protrusion would likely be approximately the same along a few microns long part of the leading edge indented by the flow and equal to that at the flat part of the leading edge at the sides of the indentation. At the onset of the recovery, the indentation at the leading edge can be approximated with two circular arcs characterized by the constant radius of curvature 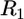(Fig. 4 C). Then, at each time interval, 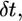the flat parts of the leading edge at the sides of the indentation would advance on the distance 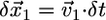, where 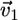is the local protrusion velocity. At the same time, each point on the arc-shaped parts of the leading edge would advance the distanc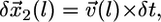e where 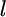is the coordinate along the leading edge, and 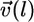is the protrusion velocity normally local to the leading edge. Importantly, 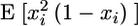Therefore, at each time interval, 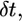the radius of curvature of the arc-shaped parts of the leading edge would increase by 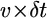: 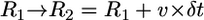(Fig. 4 C). As a result, with time the arcs flatten and look more and more like the flat leading edge around the initial indentation. It appears that the point of the intersection of the two arcs advances at the rate 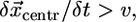faster than the leading edge, healing the indentation. Quantifying of the arc radii of curvature in the beginning of the recovery process (Fig. 4 A) shows that the rate of the radii increase is very close to the rate of advancement of the flat leading edge.

FIGURE 4.

Recovery of the leading edge shape. (A) After the readhesion, protrusion of the formerly arrested part of the leading edge results in the recovery of the initial shape. (B) TRITC-phalloidin staining of the keratocyte fixed at the moment of recovery shows F-actin accumulation at the site of the indentation. (C) Normal extension from both sides of the indentation explains the recovery of the leading edge shape in agreement with the GRE model. Bar, 10 μm; time in seconds.

Interestingly, fixation of the cells in the process of recovery and staining them with TRITC-phalloidin for F-actin demonstrated elevated actin density along the path of the intersection of the two arc-shaped sides of the indentation (Fig. 4 B). Actin density in this strip was approximately twice the density of the surrounding regions. This could be explained by the overlap of the two actin networks growing in normal direction from both sides of the indentation.

Force estimate

We measured the velocity of the flow by mixing plastic beads with the fluid in the micropipette and tracing the bead trajectories at finite time intervals at various distances, as described in Materials and Methods (see Fig. 6 A). The stationary laminar flow field (characterized by Reynolds numbers of the order of unity) develops such that its velocity is almost horizontal away from the pipette tip. The velocity decreases at a constant height above the surface away from the pipette tip. It also increases in the vertical direction away from the surface (Fig. 2 E), thus generating the shear stress on the surface of the lamellipodium, stalling the advancement of the cell. In addition, the flow causes the gradual increase of the hydrostatic pressure closer to the pipette, contributing to the arrest of the cell protrusion. The resulting hydrodynamic load increases when the leading edge gets closer to the pipette tip. To compute the arresting force, we simulated the fluid flow numerically (Fig. 5 A, Materials and Methods) modeling the lamellipodium as a 0.2 μm step on the flat surface. Then, to estimate the hydrodynamic load on the cell body, we simulated the flow representing the cell body by the upper half of the 18 μm × 12 μm × 12 μm ellipsoid (Fig. 5 C, Materials and Methods). Finally, to find out if the force on the lifted lamellipodium tip is similar to the arresting force on the flat lamellipodium, we simulated the flow in the corresponding geometry (Fig. 5 D, Materials and Methods).

To confirm that the computed velocity field matches that created experimentally, we found numerically the rate of flow at the pipette tip at which the horizontal component of the computed fluid velocity along the horizontal straight line (from the tip in the direction opposite to that of the cell movement) matches the experimental data corrected for the systematic error (Fig. 6 B, Materials and Methods). The fitting is done between 10 and 40 μm from the pipette tip. Closer to the tip the errors of measurement method causes the underestimation of the velocity (Materials and Methods).

We observe that the leading edge gets arrested when it is from 3 to 6 μm away from the pipette tip in the horizontal direction, so we computed the pressure on the front edge of the lamellipodium step and the shear stress distribution on its dorsal surface (Fig. 5 A, Materials and Methods). Surprisingly, the results showed very weak shear stress of the order of 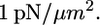To illustrate the characteristic arresting forces, we computed the pressure on one micron long part of the front lamellipodium edge and the total shear force on 1 μm × 1 μm square on the frontal part of the lamellipodium dorsal surface. When the leading edge is 3 μm (6) away from the pipette tip, the pressure per 1 μm of the leading edge is ≈1 (0.5) pN, and the shear force on 1 μm² of the lamellipodium dorsal surface is ≈13 pN (5).

Note, that the stress level curves (curves where the shear stress is constant) on the dorsal lamellipodium surface (Fig. 5 B) are very similar to the shape of the indentation of the arrested lamellipodial edge (Fig. 1 A and Supplementary Movie 1), indicating that certain threshold shear stress in the piconewtons range per square micron abruptly arrests the protrusion. Simulation of the flow impinging on the lifted 1 μm tip of the lamellipodium leading edge (Fig. 5 D, Materials and Methods) demonstrated that the total arresting force increases, mainly due to greater contribution from hydrostatic pressure on the lifted ventral surface, but not significantly, just by a few piconewtons per micron.

Finally, we computed the flow around the cell body (Fig. 5 C, Materials and Methods) and estimated the total hydrodynamic load (integral of the horizontal components of the pressure and shear stress over the cell body surface) on the cell body. The resulting estimate is ≈65 pN, so we conclude that the force of a few tens of piconewtons does not affect the forward translocation of the keratocyte's cell body.

DISCUSSION

In this work, we report that fluid flow arrests the lamellipodium protrusion locally (only a few microns long part of the leading edge closest to the pipette is stalled) and directionally (flow parallel to the leading edge does not affect locomotion). Global directional cell response to both shear flow (37) and external force in general (38) is a well known phenomenon. Its nature is complex and poorly understood, but it is clear that the corresponding mechanisms involve modulating the biophysical force of tractions through rho GTPase-mediated biochemical pathways (39) and signaling adhesion proteins (40). These pathways usually induce global changes on the scale of tens of microns (41), leading us to suggest that what we observed was a different and novel phenomenon of local mechanical arrest of the cell leading edge protrusion by the shear flow. An additional argument in favor of this hypothesis is that the flow parallel to the leading edge would induce at least some changes in motility if the biochemical pathways were involved. Also, the contour of the stalled leading edge is very similar to the shear stress level curves, suggesting that certain critical force stops the protrusion.

Our results suggest that the hydrodynamic load in the range of piconewtons per micron neither stalls actin polymerization, nor disrupts existing adhesions behind the leading edge, nor causes retrograde flow of the lamellipodium actin network. These results agree with the existent estimates of the polymerization, contraction, and adhesion forces in the lamellipodium: at least hundreds of piconewtons per micron would be necessary to stall polymerization and/or to turn the protrusion into the retrograde flow (see Introduction). Therefore, some other explanation of how the weak force arrests the protrusion must be found.

The simplest possibility would be that the shear force buckles the lamellipodial actin network lifting it up, but the following estimates show that this would require force magnitude greater than observed. The initial width of the rim of the lamellipodium that looses its adhesion is a few tenths of a micron. The critical force that would buckle an elastic sheet of such width is 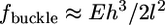(42), where 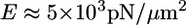(43) is the Young's modulus of the actin network, 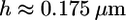(2) is the thickness of the lamellipodium, and 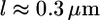is the width of the rim. Substituting the estimates of the mechanical characteristics of the lamellipodium, we obtain the value of 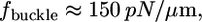one to two orders of magnitude greater than the observed stall force. In fact, at the microscopic scale of a few tenths of a micron, applicability of continuum mechanics is questionable, but if we estimate the force required to buckle a single actin filament a few tenths of a micron long and multiply this estimate by the number of filaments per micron of the leading edge, we would again obtain hundreds of piconewtons per micron (5). Experimentally, the force to bend the ruffle at the fibroblast leading edge was estimated in the nanonewtons range (15), also suggesting that we observed a different phenomenon than buckling of the actin network.

We propose the following plausible explanation for the protrusion arrest by the weak force. The observed abruptness of the stall, the emergence of the very narrow zone at the lamellipodium tip where the flow interferes with the nascent adhesions, and the coincidence of the profile of the stalled lamellipodium edge with the shear stress level curve suggest that a critical shear force interferes with the nascent adhesions at the very tip of the lamellipodium. Keratocytes have a rim of close contacts at the lamellipodium tip where new cell-substrate adhesions are formed. Importantly, the adhesions are assembled hierarchically, so that very few essential molecules assemble first with other types of adhesion proteins adding up later in certain order (30,44). The adhesions are stationary relative to the substrate, whereas the leading edge continues to protrude, so the nascent adhesions mature at a certain distance beyond the lamellipodium tip (30). Therefore, it is possible that the nascent, immature adhesions in the narrow, few tenths of a micron wide zone at the lamellipodium tip are initially very weak, and their adhesion energy is much smaller than the one estimated for mature adhesions. The force of the shear flow could therefore be sufficient to interfere with these nascent adhesions, perturbing the formation of strong mature adhesions.

When the flow is interfering with these nascent adhesions, there is a possibility other than the buckling and bending of the actin network, namely, reorienting new actin filaments upward, away from being parallel to the substrate. Indeed, the Arp2/3-mediated nucleation of nascent filaments from the sides and/or tips of existent filaments (reviewed in Pollard and Borisy (3)) preserves the magnitude of the angle between the “mother and daughter” filaments but does not prescribe the 3D orientation. Therefore, nascent filaments can be nucleated at such angles that, cross-linked, they become (Fig. 2 E) a flat sheet that “ruffles up”, loosing contact with the substrate. This would be energetically advantageous since, though the adhesion energy would be lost, the hydrodynamic load would push this lifted actin network backward, decreasing its free energy. Interestingly, the lifted part of the edge was shown to contain an elevated level of the component of nascent adhesions at the lamellipodial tip, integrin β-1 (Fig. 2 B). This finding reinforces our conclusion that the flow causes arrest of the edge by interfering with the nascent adhesions mechanically, rather than by altering their chemical composition through signaling pathways. The relative accumulation of the integrin β-1 in the lifted edge as compared to the neighboring adherent regions may be explained by the arrest of the integrin β-1 turnover due to the fact that the substrate adhesions could not form and mature.

One additional indication of the importance of the nascent adhesion at the lamellipodium tip is our observation that the protrusion resumes when the flow stops only after the readhesion takes place. The “side zippering” character of the readhesion process suggests that, in the absence of the resisting force, the nascent filaments and adhesions appear rapidly and cooperatively from the sides of the lifted part of the lamellipodium, which are closest to the substrate. The role of the nascent adhesions could therefore be to keep the lamellipodium adherent, whereas the interplay between the weak nascent adhesions at the tip and an external force determines if the lamellipodium stays flat or ruffles up. Similar competition between the nascent adhesions and some kind of a resisting force could be involved in the natural ruffling process, which is common at the leading edge of many cell types other than keratocytes (45). Resisting force could be an increased membrane tension or a contractile force developing in the lamellipodial sheet. The important point is that only a few piconewtons per micron of the leading edge are sufficient to prevent adherent flat protrusion and induce ruffling.

Another valuable result of our study is that the force of tens of piconewtons does not affect the forward translocation of the keratocyte cell body. This result is not surprising, because thousands of piconewtons are developed by actin-myosin contraction and applied to the substrate in motile keratocytes (24), yet it is still nontrivial, because the traction forces in the keratocyte's anterior-posterior direction are much weaker than strong “pinching” sideways forces and were not measured accurately. Also, our observation of the “healing” of the indentation at the leading edge lends additional support to the GRE model of protrusion (36).

The limitation of our method of estimating the force is that microscopic hydrodynamics is sensitive to a number of factors that are hard to control, such as possible changes of viscosity close to the surface and the nature of boundary conditions at the cell membrane-fluid interface. In addition to the errors of velocity measurements at the small distances described above, these uncertainties make our force estimate only an order of magnitude accurate. However, the advantage of our method is its simplicity. Our study also suggests that the stall force would depend on the adhesion strength and probably not on biophysical properties of the actin network at the leading edge. These predictions can be tested by using substrata of varying adhesivity and by controlling the actin rheology (for example, by inhibiting or overexpressing actin accessory proteins).

The role of the adhesion as a stabilizer of the protrusion by being a “clutch” that has to be engaged to translate the growth of the actin network into the extension of the leading edge is well known (6). However, previous studies investigated this role “globally”, on the scale of the whole lamellipodium and usually by means of a biochemical perturbation of various cell motility processes. Our study, for the first time, to our knowledge, addresses this problem locally (at the very leading edge of the cell), mechanically and quantitatively, by applying a weak local force of known magnitude to the growing actin filaments and adhesions simultaneously. Similar responses observed in migrating keratocytes and spreading fibroblasts suggest that sensitivity of the protrusion to a weak local force is likely a phenomenon common to all motile cells.

Weak and flexible leading edge may be a useful feature for the cell to ensure maximal protrusion in the direction of the lesser external force helping to find a path in a complex environment. A small fluid shear stress on the order of piconewtons per square micron would be physiologically relevant because, for example, blood flow of such magnitude (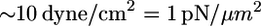) causes a hierarchy of responses in endothelial cells, including those that are motile. Coupled maturation of nascent adhesions and force application enables the cell to pull itself forward through this path. In general, our observations reinforce the concept of intimate coupling of protrusion and adhesion molecular machineries at the leading edge (46). We are tempted to speculate that although growth of the lamellipodium actin sheet is a strong process not discriminating between possible directions, it is the weak and sensitive adhesion at the very tip of the protruding lamellipodium that locally determines the overall shape and direction of migrating cells. Data indicating that microtubules govern cell directionality by targeting adhesions (47) is in line with this idea, but much more research is needed before the interplay between adhesion and protrusion will be fully understood.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.