A base triple in the Tetrahymena group I core affects the reaction equilibrium via a threshold effect

Abstract

Previous work on group I introns has suggested that a central base triple might be more important for the first rather than the second step of self-splicing, leading to a model in which the base triple undergoes a conformational change during self-splicing. Here, we use the well-characterized L-21 ScaI ribozyme derived from the Tetrahymena group I intron to probe the effects of base-triple disruption on individual reaction steps. Consistent with previous results, reaction of a ternary complex mimicking the first chemical step in self-splicing is slowed by mutations in this base triple, whereas reaction of a ternary complex mimicking the second step of self-splicing is not. Paradoxically, mechanistic dissection of the base-triple disruption mutants indicates that active site binding is weakened uniformly for the 5′-splice site and the 5′-exon analog, mimics for the species bound in the first and second step of self-splicing. Nevertheless, the 5′-exon analog remains bound at the active site, whereas the 5′-splice site analog does not. This differential effect arises despite the uniform destabilization, because the wild-type ribozyme binds the 5′-exon analog more strongly in the active site than in the 5′-splice site analog. Thus, binding into the active site constitutes an additional barrier to reaction of the 5′-splice site analog, but not the 5′-exon analog, resulting in a reduced reaction rate constant for the first step analog, but not the second step analog. This threshold model explains the self-splicing observations without the need to invoke a conformational change involving the base triple, and underscores the importance of quantitative dissection for the interpretation of effects from mutations.

INTRODUCTION

Functional RNAs participate in a number of multistep processes that require conformational changes as part of a normal catalytic cycle. These processes include protein synthesis by the ribosome and pre-mRNA splicing by the spliceosome (e.g., Raghunathan and Guthrie 1998; Staley and Guthrie 1999; Pape et al. 2000; Ogle et al. 2002). Conformational changes are also required for the self-splicing reaction of group I and group II introns, and some evidence for such conformational transitions has been presented (Chanfreau and Jacquier 1996; Golden and Cech 1996). The self-splicing introns offer particularly appealing systems to study functional conformational transitions of RNA, as these systems are complex enough to require such rearrangements, but are far simpler than such multicomponent molecular machines as the ribosome or the spliceosome.

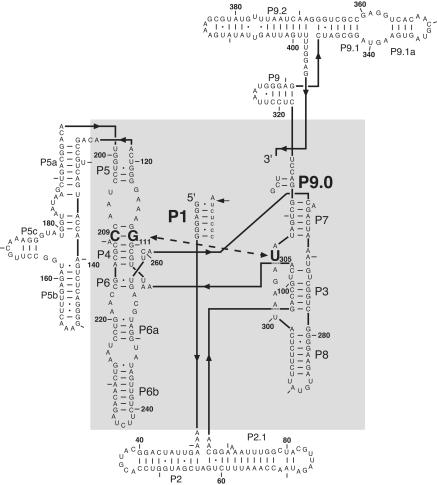
Using a combination of site-directed mutagenesis and kinetic measurements, Tanner and Cech (1997) showed that a base triple in the group I intron core was important for splicing activity. Because this triple [(G₁₁₁·C₂₀₉)·U₃₀₅ in Tetrahymena, see Fig. 1 ▶] connects the P4/P6 domain with the P3/P7/P8 domain, it was suggested that this triple ties together the core of the ribozyme, thereby allowing formation of the exon-binding site (Michel and Westhof 1990; Tanner and Cech 1997). This notion was confirmed in the recent crystal structure of the Azoarcus intron (Adams et al. 2004). Additionally, it was suggested that the base triple is formed during the first, but not the second step of self-splicing, implying its involvement in a conformational change between the two chemical steps of self-splicing (Tanner et al. 1997). This proposal was based on the observation that disruption of the base triple resulted in disappearance of a splicing intermediate, suggesting that the first step of self-splicing was slowed more than the second step.

FIGURE 1.

Secondary structure of the L-21 ScaI group I ribozyme from Tetrahymena thermophila. This schematic representation shows the secondary structure in the topology of the tertiary structure (Golden et al. 1998). The (G₁₁₁·C₂₀₉)·U₃₀₅ base triple is highlighted in bold, as are P1 and P9.0 formed in trans with oligonucleotide substrate S and UCG, respectively. The RNA core that is conserved between all subclasses of group I introns is shown in the gray-shaded area (Michel and Westhof 1990).

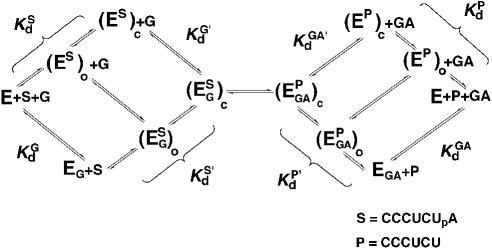
Here, we use the well-characterized Tetrahymena ribozyme system, in which splice site analogs are added in trans to further explore the role of the (G₁₁₁·C₂₀₉)·U₃₀₅ base triple. The extensive prior kinetic and thermodynamic framework for this ribozyme renders it an ideal system for probing the role of particular interactions and the effects of mutations (Fig. 2 ▶; Strobel and Cech 1996; Narlikar and Herschlag 1998; Szewczak et al. 1998, 2002; Shan et al. 2001; Karbstein et al. 2002; Shan and Herschlag 2002). In addition, the ribozyme is fully active, so that kinetic results are not confounded by intron constructs with only fractional occupancy of the active state and potentially rate-limiting conformational changes from inactive to active forms (e.g., Walstrum and Uhlenbeck 1990; Woodson and Cech 1991; Emerick and Woodson 1993; Emerick et al. 1996).

FIGURE 2.

Thermodynamic framework for the group I ribozyme reaction (e.g., Herschlag and Cech 1990; Bevilacqua et al. 1992; McConnell et al. 1993). (E^s)_o and (E^s)_c [or (E^P)_o and (E^P)_c] refer to the open and closed conformations of the P1 duplex, in which tertiary interactions between the ribozyme core are absent and present, respectively.

We show herein that disruption of the base triple slows the forward ribozyme reaction but not the reverse reaction, analogous to the differential effects on the first and second step in self-splicing. Nevertheless, additional experiments provide strong evidence that the base triple is formed with both bound substrates and bound products. These paradoxical observations can be traced to a threshold effect on binding of reactants at the active site. Such thresholds allow uniform energetic contributions to have differential observed effects, and can thereby serve important biological functions while confounding interpretation of site-directed mutagenesis results.

RESULTS AND DISCUSSION

As noted in the Introduction, previous work on the group I self-splicing introns from Tetrahymena and Anabaena suggested the formation of a base triple that positions the P4–P6 domain of the ribozyme with respect to the P3–P7–P8 domain, and further suggested that this base triple was involved in mediating conformational changes between the two steps of self-splicing (Tanner and Cech 1997; Tanner et al. 1997; Adams et al. 2004). To further investigate and quantitate the effect from base-triple disruption on individual steps of the group I self-splicing reaction, we used the Tetrahymena L-21 ScaI ribozyme. The L-21 ScaI ribozyme is well suited for such a study, as individual reaction steps have been identified and their kinetics and thermodynamics have been quantitatively described (Fig. 2 ▶; Herschlag and Cech 1990; Bevilacqua et al. 1992, 1993; McConnell et al. 1993; Knitt et al. 1994; Narlikar et al. 1995; Narlikar and Herschlag 1996; Shan and Herschlag 1999; Karbstein et al. 2002). Furthermore, the ribozyme system, in contrast to the self-splicing system, is not confounded by slow exchange from inactive conformations. The experiments herein involve the same mutants used in the previous work (Tanner et al. 1997), except that they are investigated in the ribozyme instead of the self-splicing background; the wild-type base triple (G₁₁₁·C₂₀₉)·U₃₀₅ is disrupted by a switch in the base pairing residues to (C₁₁₁·G₂₀₉) or a change in the third base from U₃₀₅ to C₃₀₅, and isosteric interactions are restored in the triple mutant (C₁₁₁·G₂₀₉)·C₃₀₅ (Fig. 1 ▶; see Tanner et al. 1997 for a pictorial representation).

Disrupting the (G₁₁₁·C₂₀₉)·U₃₀₅ triple affects the forward but not the reverse reaction

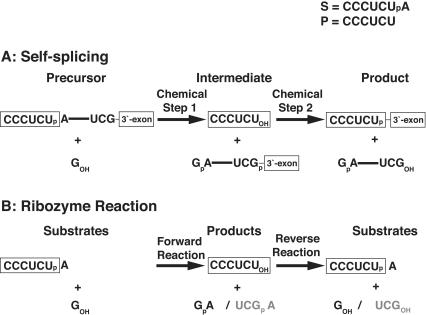
To test whether base-triple disruption has an effect on the ribozyme reaction akin to the self-splicing reaction, we measured the rate constants (k_cat/K_m)^G and (k_cat/K_m)^GA for the forward and reverse reaction, respectively. The rate constants (k_cat/K_m)^G and (k_cat/K_m)^GA describe the reaction from E·S and free G (or from E·P and free GA, Eq. 1) and, therefore, include contributions from binding of G (or GA) and reactivity of the E·S·G (or E·P·GA) complex. These reactions are analogous to the first and second self-splicing steps, as described below (Scheme 1 ▶).

SCHEME 1.

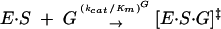(1a)

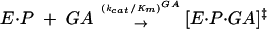(1b)

Disrupting the (G₁₁₁·C₂₀₉)·U₃₀₅ triple decreases (k_cat/K_m) six- and 30-fold for the C₃₀₅ and (C₁₁₁·G₂₀₉) mutants, respectively, although not affecting (k_cat/K_m)^GA significantly (Table 1 ▶). Thereby, the ratio of (k_cat/K_m)^G to (k_cat/K_m)^GA is decreased five- and 50-fold for the C₃₀₅ and (C₁₁₁·G₂₀₉) mutants, respectively. In the compensatory triple mutant (C₁₁₁·G₂₀₉)·C₃₀₅, the wild-type value of (k_cat/K_m) ^G is restored and even exceeds the wild-type value by approximately sixfold (Table 1 ▶). Thus, binding of G and/or reactivity of the E·S·G complex is affected by changes in the base triple, but not binding of GA or reactivity of the E·P·GA ternary complex.

TABLE 1.

Effect of disruption of the base triple on the reaction equilibrium

	(kcat/Km)G	(kcat/Km)GA	(kcat/Km)G
Ribozyme	(M−1 min−1)	((kcat/Km)GA
Wild type	280 ± 60	1.9 ± 0.1	150 ± 24
C305	50 ± 14	1.5 ± 0.1	33 ± 7
(C111·G209)	10 ± 5	3.0 ± 0.4	33 ± 1.6
(C111 · G209) · C305)	1820 ± 300	3.0 ± 1.5	610 ± 80

All experiments were performed at 30°C, pH 7.2. −1d,rSA and −1d,rP were used to ensure that the chemical step was rate-limiting in all cases.

In the previous self-splicing experiments, the base-triple disruptions were found to have a larger effect on the first step than on the second step. The results herein are analogous to the self-splicing results. This is because in the forward ribozyme reaction, a 5′-splice site analog, S, reacts with guanosine (G), to form a 5′-exon analog, P, and GA, analogous to the first step of self-splicing (Scheme 1 ▶, left). The reverse ribozyme reaction, between GA and the 5′-exon analog P, similarly resembles the second step of self-splicing (Scheme 1 ▶, center).

Disrupting the (G₁₁₁·C₂₀₉)·U₃₀₅ base triple weakens binding of S

We next set out to determine which of the individual reaction steps was affected by disruption of the base triple. We first describe briefly the individual reaction steps of the ribozyme reaction (Fig. 2 ▶). Previous work has shown that S (and P) binding occurs in two steps, formation of a helix between S (or P) and the Internal Guide Sequence (IGS) of the ribozyme to give the P1 duplex bound in a so-called open complex [(E· S)_o or (E·P)_o in Fig. 2 ▶] and subsequent docking of the P1 duplex into tertiary interactions at the active site to give the so-called closed complex [(E·S)_c or (E·P)_c in Fig. 2 ▶; e.g., Pyle and Cech 1991; Bevilacqua et al. 1992; Herschlag 1992; Strobel and Cech 1993; Narlikar and Herschlag 1996; Bartley et al. 2003]. Binding of S and G (or P and GA) is not ordered and can occur through the top or bottom pathway, or the hybrid pathway in which G (or GA) binds to the (E·S)_o [(or E·P)_o] complex in Figure 2 ▶. For wild-type S [or P, i.e., with all ribose residues; note that a deoxyribose residue at the cleavage site does not affect docking (Narlikar et al. 1997); −1d,rSA, Chart 1 ▶] and wild-type ribozyme, docking of the P1 duplex is favorable, leading to accumulation of the (E·S)_c [or (E·P)_c] complex. However, certain modifications within the ribozyme or S strands of the P1 duplex disfavor the docked state, leading to stable accumulation of the (E·S)_o complex (e.g., Herschlag et al. 1993; Strobel and Cech 1995, 1996; Narlikar and Herschlag 1996, 1998). Reaction can only proceed after formation of the closed, ternary complex, (E·S·G)_c [or (E·P·GA)_c], and the chemical step is preceded by loss of a proton, presumably from the attacking 3′-hydroxyl group of G in the forward reaction or the attacking 3′-hydroxyl group of P in the reverse reaction (Knitt and Herschlag 1996; Karbstein et al. 2002).

CHART 1.

Oligonucleotide substrates and their abbreviations and properties

Abbreviation	Oligonucleotide	Attributes
5′-Splice- site Analogs
	Position: −3 −1 +1
−1d,Rsa	rC rC rC rU rC dT rA	Wild type, with slow chemical step
−1d,−3m,rSA	rC rC rC mU rC dT rA rA4	Undocked
−1d,rSA5	rC rC rC mU rC dT rA rA4	A5 tail interferes with P9.0
5′-Exon Analogs
	Position: −3 −1
−1d,rP	rC rC rC rU rC dT	Wild type, with slow chemical step

Note: r = 2′-OH; d = 2′-H, m = 2′-OCH₃

We first determined the effect of the base-triple mutation on the affinity for S. Effects on binding of S were determined by measuring dissociation rate constants, as S and P oligonucleotides have been shown to bind to ribozymes with essentially unchanged association rate constants, presumably because this association is limited by a simple duplex formation between the ribozyme’s IGS and the oligo-nucleotide (Herschlag and Cech 1990; Knitt and Herschlag 1996; Narlikar et al. 1999; Karbstein et al. 2002). For simplicity, the effects on S (and P, below) binding are reported as equilibrium dissociation constants with an assumed constant association rate constant of 10⁸ M⁻¹min⁻¹ (Herschlag and Cech 1990; Knitt and Herschlag 1996; Narlikar et al. 1999; Karbstein et al. 2002).

Native gel-pulse chase experiments were used to obtain dissociation rate constants and affinities for S for the base-triple ribozyme variants. Disruption of the base triple by either mutation weakened S affinity by 15- to 20-fold, and the compensatory base-triple mutant restores wild-type affinity to within threefold (Table 2 ▶). The affinity for S in the disrupting mutants is consistent with S bound in the open complex (K_d,open = 2.0 nM and K_d,closed = 0.18 nM for wild-type ribozyme; K_d,obs = 3.4 and 2.8 nM for the C₃₀₅ and the mutants, respectively, (Table 2 ▶; data not (C₁₁₁·G₂₀₉) shown). This observation suggests that disrupting the base triple disrupts interactions required for P1 docking, consistent with the suggested role of the triple in aligning the P4–P6 domain with respect to the P3–P7–P8 domain, the two regions that appear to provide the docking interface for P1 (Michel and Westhof 1990; Tanner and Cech 1997; Golden et al. 1998; Szewczak et al. 1998; Adams et al. 2004).

TABLE 2.

Effect of disruption of the base triple on binding of 5′-splice site and 5′-exon analogs (S and P)

Ribozyme	KSd(nM)	kc(min−1)	KdP (nM)	K−c (min−1)
Wild type	0.18 ± 0.02	0.036 ± 0.06	8.8 ·10−3± 2 3 ·10−3	0.22 ± 0.03
C305	3.4 ± 0.2	0.013 ± 0.05	0.19 ± 0.03	0.14 ± 0.01
(C111 ·G209)	2.8 ± 0.2	0.0070 ± 0.003	0.94 ± 0.06	0.25 ± 0.01
(C111 · G209) ·C305	0.51 ± 0.01	0.019 ± 0.02	8.4 ·10−3± 9 3 ·10−4	0.18 ± 0.02

All experiments were performed at 30°C and pH 7.2 using −1d,rSA and −1d,rP. Dissociation constant for S and P were calculated from the dissociation rate constants determined in gel-shift experiments and the association rate constant of 10⁸ M⁻¹ min⁻¹ (Herschlag and Cech, 1990; Knitt and Herschlag 1996; Karbstein et al 2002). k_c values were obtained from the plateau of reaction rate constant dependences on G concentration and represent the rate constant at saturating G and S. k_−c values were obtained from the plateau of the rate constant of the reverse reaction at high AUCGA concentration and represent the rate constant at saturating AUCGA and P. The faster rate constants for the reverse reaction relative to the forward reaction can be explained by the use of AUCGA. Control experiments show that AUCG reacts approximately fivefold faster than G (data not shown).

Disrupting the (G₁₁₁·C₂₀₉)·U₃₀₅ base triple does not affect G affinity

We compared G binding to wild-type and mutant (E·S)_o complexes to determine whether disruption of the base triple affected G binding. Binding of G to the (E·S)_o complexes was the same, within twofold, for the wild-type and mutant ribozymes (Table 3 ▶), providing no indication of an effect of the triplex on the G binding site.

TABLE 3.

Guanosine affinity with wild-type and undocked substrate

	KGd(μM)	KGd,(E·S·G)o
Ribozyme	(E·S·G)c	(E·S·G)o	KGd(E·S·G)c
Wild type	128 ± 30	520 ± 60	4.0 ± 0.5
C305	—	400 ± 160	—
(C111 · G209)	—	220 ± 40	—
(C111 · G209) · C305	12 ± 4	350 ± 20	30 ± 8

All experiments were performed at 30°C using −1d,rSA or−1d,−3m,rSA₅ for binding in the closed and open complex, respectively. Note that no measurement of G binding to the C₃₀₅ and(C₁₁₁· G₂₀₉) mutants in the closed complex is reported because the−1d,rSA substrate does not bind to these mutants in the closed complex. Dissociation constants for G were determined from dependences of the rate constant for reaction of −1d,rSA and −1d,−3m,rSA₅ on G concentration.

Binding of G to the wild-type ribozyme is approximately fourfold stronger to the (E·S)_c complex than to free E or the (E·S)_o complex. This differential binding represents thermodynamic coupling between G binding and S docking (McConnell et al. 1993; Karbstein et al. 2002; Shan and Herschlag 2002). The similar dissociation constants for G binding to the (C₁₁₁·G₂₀₉) and C₃₀₅ mutants with bound −3m,−1d,rSA₅, which ensures formation of the open complex, and with bound −1d,rSA, the normal 5′-exon analog, provide further evidence for binding of the normal 5′-exon analog in the open rather than closed complex when (C₁₁₁·G₂₀₉) and C₃₀₅ ribozymes are used (K_d,G = 220 ± 8 and 400 ± 160 μM using −1d,rSA and −1d, −3m,rSA₅ substrates with the C₃₀₅ mutant and K_d,G = 402 ± 130 and 220 ± 40 μM using −1d,rSA and −1d, −3m,rSA₅ substrates with the (C₁₁₁·G₂₀₉) mutant (Table 3 ▶; data not shown). The coupling that is absent for the (C₁₁₁·G₂₀₉) and C₃₀₅ mutant ribozymes is restored in the compensatory mutant in which the base triple is reformed and binding in the closed complex is restored (Table 3 ▶); coupling for this variant is even stronger than for wild type (30-fold instead of fourfold; Table 3 ▶).

Direct comparison of the wild-type and mutants for G binding to the closed complex of E and S was not possible, because S does not stably dock to the (C₁₁₁·G₂₀₉) and the C₃₀₅ mutant ribozymes, as noted above.

Disrupting the (G₁₁₁·C₂₀₉)·U₃₀₅ base triple does not affect P9.0 formation

Whereas in the first step of self-splicing, G binds solely via interactions with the G binding site, the G at the 3′-splice site (′G) is preceded by a short sequence that can form a helix, termed P9.0, which helps to position ′G at the active site (Burke 1989; Michel et al. 1989; Moran et al. 1993; Russell and Herschlag 1999b; Karbstein et al. 2002; Fig. 1 ▶; Eq. 1). Thus, whereas the chemical transformations in the two steps of self-splicing are simply the reverse of one another, some of the surrounding interactions are different, including the absence or presence of the P9.0 helix. To further relate the results herein to the self-splicing reaction, we determined whether formation of the (G₁₁₁·C₂₀₉)·U₃₀₅ base triple affected the energetic contribution from the P9.0 helix.

In the ribozyme reaction, P9.0 can be formed in trans, using the analog AUCG and, for the reverse reaction, AUCGA (Moran et al. 1993; Russell and Herschlag 1999b). Table 4A ▶ compares the values for (k_cat/K_m)^AUCG and (k_cat/K_m)^G for the wild-type and mutant ribozymes. The ratio of (k_cat/K_m)^AUCG and (k_cat/K_m)^G is the same within threefold for the mutant ribozymes. Similarly, the ratio of AUCG to G-binding affinities to the (E·S)_o complex is the same within twofold for the wild-type and base-triple disruption ribozymes, indicating that P9.0 provides the same energetic contribution. Surprisingly, binding of AUCG is especially strong for the compensatory triple mutant, thereby leading to a fivefold increase in the binding ratio (Table 4A ▶); we do not understand the origin of this effect. The contribution of P9.0 in the reverse reaction with AUCGA was the same within threefold for all ribozyme forms (Table 4B ▶).

TABLE 4A.

Effect from disruption of the base triple on P9.0 formation in the forward reaction

	Kd (μM)	Ratio	(kcat/Km) (M−1 min−1)	Ratio
Ribozyme	AUCG	G	G/AUCG	AUCG	G	AUCG/G
Wild type	14.4 ± 5.2	520 ± 60	36 ± 9	9.8 · 104 ± 3000	280 ± 60	350 ± 65
C305	8.0 ± 2.0	400 ± 160	50 ± 8	7.5 · 103 ± 170	50 ± 14	150 ± 38
(C111 · G209)	19.7 ± 1.4	220 ± 40	11 ± 1	3.7 · 103 ± 300	10 ± 5	370 ± 150
(C111 · G209) · C305	2.2 ± 0.2	350 ± 10	159 ± 10	2.0 · 105 ± 7000	1820 ± 300	110 ± 14

All experiments were performed at 30°C, pH 7.2. K_d values were determined with −1d,−3m,rSA₅ to ensure formation of the open complex. −1d,rSA was used to determine (k_cat/K_m) values.

TABLE 4B.

Effect from disruption of the base triple on P9.0 formation in the reverse reaction

	(kcat/Km) (M −1 min−1)	Ratio
Ribozyme	AUCGA	GA	AUCGA/GA
Wild type	3.9 · 103 ± 1000	1.9 ± 0.1	2052 ± 418
C305	4.7 · 103 ± 500	1.5 ± 0.1	3133 ± 124
(C111 · G209)	7.1 · 103 ± 1300	3.0 ± 0.4	2367 ± 354
(C111 · G209) · C305	1.8 · 104 ± 3000	3.0 ± 1.5	6000 ± 800

All experiments were performed at 30°C, pH 7.2. −1d,rP was used to ensure that the chemical step was rate-limiting in all cases.

Disrupting the (G₁₁₁·C₂₀₉)·U₃₀₅ base triple has little or no effect on the chemical step

To investigate whether the base triple affected the actual transformation of the ternary complex of bound substrates or products, we directly determined these single turnover reaction rate constants. There were modest effects for reaction of E·G·S upon disruption of the base triple, and this effect was rescued upon restoration of the base triple (Table 2 ▶). However, as noted above, the mutants with disrupted base triples bind S in the open, rather than closed complex that is required for reaction. Thus, the modest observed effects of three- and fivefold could result from an additional energetic barrier to form the reactive, closed complex (see Herschlag et al. 1993; Knitt et al. 1994; Narlikar et al. 1999; Engelhardt et al. 2000). For the reverse reaction, which starts from (E·P·AUCGA)_c for the wild-type and mutant ribozymes (see below), there is no effect of the mutations on the reaction rate (Table 2 ▶). This observation strongly suggests that disruption of the base triple does not affect the chemical-transition state, so that disruption of docking interactions can account for the observed effects on (k_cat/K_m)^G and k_c. Support for this conclusion is presented in the next section.

Disrupting the (G₁₁₁·C₂₀₉)·U₃₀₅ base triple weakens binding of P

The absence of an effect of the mutations on the reverse reaction of E·P with GA and of the E·P·AUCGA ternary complex was consistent with an absence of a role of the base triple in the reverse ribozyme reaction, analogous to the proposed absence of an effect on the second self-splicing step (see Scheme 1 ▶ and above). However, direct investigation of the binding affinity of the 5′-exon analog P revealed an effect of the base-triple mutations analogous to that observed with the 5′-splice site analog S.

Binding of P was determined from the association rate constant of 10⁸ M⁻¹min⁻¹, as noted above, and from the dissociation rate constants obtained in native gel-pulse chase experiments. Binding of P to free E is weakened ~20-and 100-fold in the C₃₀₅ and (C₁₁₁·G₂₀₉) mutants, respectively, and wild-type affinity is restored in the compensatory triple mutant (Table 2 ▶). Not only is binding of the 5′-exon analog weakened, but the effect is larger than that for binding of S. Nevertheless, reactivity of bound S was affected more strongly than reactivity of bound P (see above). Below, we describe a model that reconciles these paradoxical observations and quantitatively accounts for their origin.

A threshold model accounts for the differential effects of base-triplet disruption on the first and second step of self-splicing

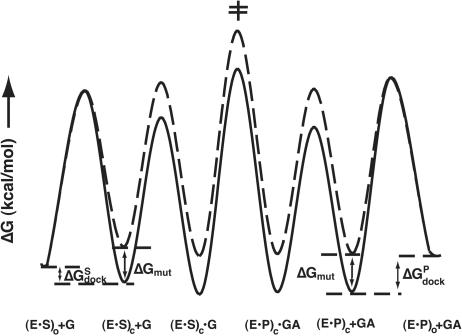
The weaker binding of S and P and the modest effects on binding of G with a docked but not an undocked substrate for the (C₁₁₁·G₂₀₉) and the C₃₀₅ mutants suggests that disrupting the (G₁₁₁·C₂₀₉)·U₃₀₅ base triple weakens docking of the P1 duplex into tertiary interactions with the ribozyme core. This conclusion is consistent with the importance of the (G₁₁₁·C₂₀₉)·U₃₀₅ base triple for alignment of the interface between P4/P6 and P3/P7/P9 for P1 docking (Tanner and Cech 1997; Szewczak et al. 1998; Adams et al. 2004). Below, we show that such an effect on docking can quantitatively account for all of the effects observed with the base-triple mutants according to the free-energy reaction profile in Figure 3 ▶.

FIGURE 3.

Quantitative free-energy profile for the group I reaction with wild-type and (C₁₁₁·G₂₀₉) ribozyme. The free-energy profiles were calculated at 30°C (pH 7.2) and for a standard state of 1 mM G and GA. In the case of the reaction with wild-type ribozyme (continuous line), the reaction described by (k_cat/K_m)^G is from (E·S)_c + G and the transition state for the chemical step (‡). For the (C₁₁₁·G₂₀₉) mutant (broken line), the reaction described by (k_cat/K_m)^G is from (E·S)_o + G, and the transition state of the chemical step (‡), and thus includes the additional barrier for docking. The free-energy profile was calculated as outlined in the Materials and Methods using the values listed in Table 6 ▶.

The data of Table 2 ▶ suggest that docking is destabilized sufficiently to change the ground state for bound S from the closed to the open state [(E·S)_c to (E·S)_o; Fig. 3 ▶, solid vs.broken line]. We have shown directly that base-triple disruption does not affect G binding, so this step is drawn the same for both the wild-type and mutant ribozymes in Figure 3 ▶. The results above for reaction of the E·P·AUCGA complex indicate that the chemical reactivity is not affected in the reverse reaction;² on the basis of this observation, we assume that the same holds for reaction of the E·S·G closed complex, and this assumption is supported by the self-consistency of the data for the forward and reverse reactions in the model of Figure 3 ▶, as described below. We therefore show the free energy difference between the (E·S)_c complex and the transition state for the chemical step (‡) to be the same for the wild-type and mutant ribozymes (Fig. 3 ▶). For the mutant, however, there is an additional barrier to reaction of the E·S complex, because the starting ground state is the (E·S)_o complex instead of the (E·S)_c complex. This additional energetic cost is responsible for the observed slower reaction of the mutant ribozymes. According to Figure 3 ▶, the size of this additional barrier is determined by the detrimental effect of the triple mutation (ΔG_mut) and the equilibrium for docking in the wild-type case (ΔG_dock).

Because the equilibrium for docking of P is larger than the equilibrium for docking of S (Bevilacqua et al. 1994; Narlikar et al. 1995) (ΔG^P_dock < ΔG^S_dock), the reverse reaction with bound P is predicted to be affected less than that for reaction of bound S from destabilized docking. If the perturbation is less than the overall docking energy (i.e., if the absolute value |ΔG_mut| < |ΔG_dock|), then no significant effect will be observed on reaction of bound P; the entire energetic effect, ΔG_mut, will instead be manifest on P affinity, as observed herein where P binding is weakened more than binding of S, whereas its reactivity is unaffected (Tables 1 ▶, 2 ▶). According to this model (Fig. 3 ▶), the uniform destabilization of the (E·S)_c and (E·P)_c complexes leads, paradoxically, to differential effects in the forward and reverse reaction because of the different threshold for docking of S and P.

To show that the model of uniform destabilization of the docked state can account for the data herein, the destabilization of the docked state with S and P is compared (Table 5 ▶). P remains docked on the mutant ribozymes as suggested by the lack of an effect on reactivity of the E·P·AUCGA complex (Tables 2 ▶, 4B ▶), and as also suggested by the affinity of P, which is slightly stronger than the affinity for S, even though P lacks stacking interactions that strengthen binding of S relative to P (Narlikar et al. 1995; Table 2 ▶). Because P remains docked, the difference in affinity of P between wild-type and mutant ribozymes provides a direct readout for the amount of destabilization of docking from the mutants. As shown in Table 2 ▶, this destabilization amounts to 22-and 107-fold for the C₃₀₅ and the (C₁₁₁·G₂₀₉) mutants, respectively. Because S undocks, the equilibrium constant for docking of S, K_dock, to wild-type ribozyme provides a lower limit for the amount of destabilization of S. The value for K_dock of 22 (Bartley et al. 2003) and the approximately three- and fivefold effects on k_c for the C₃₀₅ and the (C₁₁₁·G₂₀₉) mutants, respectively, can be combined to obtain an estimate for the amount of destabilization of S docking (Table 5 ▶; see Materials and Methods for details of the calculation). For the (C₁₁₁·G₂₀₉) mutant, these calculations give a uniform destabilization of docking of S and P of 107-and 90-fold. For the C₃₀₅ mutant, the calculations show a twofold difference, which could arise from a small additional effect or from combined errors in measurements with small differences. We conclude that the threshold model provides a reasonable description of the effects from these mutations.

TABLE 5.

Uniform effects from mutations on docking of S and P

Ribozyme	KPmut	KSmut
C305	22	40
(C111 · G209)	107	90

K_mut^S and K_mut^P represent the fold-effect from the base triple mutations on the docking equilibrium for S and P, respectively; for both mutants cases the docking equilibrium is destabilized. Values for K_mut^P were obtained directly from the difference in affinity of P to wild type and mutant ribozymes (Table 2 ▶). Values for K_mut^S were obtained from the equilibrium constant for docking of substrate to wild-type ribozyme, K_dock,wt and the difference in reaction rate constant k_c between wild-type and mutant ribozymes (Table 2 ▶) as described in the Materials and Methods.

Implications for self-splicing

Reaction of S with G resembles the first step of self-splicing, whereas reaction of P with AUCGA resembles the second step of self-splicing (Eq. 1). Thus, our results predict that during self-splicing, the base-triple disruptions slow the first step of self-splicing, for which there is now an additional barrier, although not affecting the second step of self-splicing. Previous work has shown exactly this behavior (Tanner et al. 1997). Whereas it was suggested in the previous work that this observation was due to a conformational change that disrupted this base triple, our data show that such a model does not need to be invoked, and suggest that, instead, the effects on splicing are the result from the different threshold for undocking of S and P as described above.

General implications

Threshold effects result from the occurrence of distinct binding modes, either as a result of mutagenesis or substrate alterations, as shown here for the group I intron, or as part of their functional reaction cycle. Examples for the latter include nonspecific binding modes of DNA-binding proteins, such as restriction endonucleases and aminoacyl-tRNA binding to the ribosome prior to accommodation in the active site. In these cases, the distinct binding modes are used as components in systems evolved to achieve high specificity. Appreciating the balance between these highly evolved states is therefore critical not only for interpreting experimental observations, as shown herein, but also for a full understanding of the functioning of biological machines and systems.

MATERIALS AND METHODS

Materials

L-21 ScaI ribozyme and its mutants were transcribed and purified over an RNeasy column (QIAGEN) or via gel-purification as described previously (Russell and Herschlag 1999b; Karbstein et al. 2002). Ribozyme mutants were constructed via the Quikchange method (Stratagene). Clones were sequenced to verify the correct sequence.

RNA oligonucleotides were purchased from Dharmacon Research, Inc. Chart 1 ▶ lists the oligonucleotides used in these studies. RNA oligonucleotides were 5′-end-labeled using γ[³²P]ATP and T4 polynucleotide kinase and were gel-purified using standard procedures (Zaug et al. 1988). RNA oligonucleotides used unlabeled were purified by anion exchange HPLC (NucleoPak, Dionex) and desalted on Sep-Pak C-18 columns (Waters).

General kinetic methods

All reactions were single turnover and, unless otherwise noted, were carried out with L-21 ScaI ribozyme at 30°C in 50 mM Na-MOPS (pH 7.2) and 10 mM MgCl₂. Prior to reaction, ribozyme was preincubated for 30 min at 50°C (pH 6.0) with 10 mM MgCl₂ to allow folding to the active state (Herschlag and Cech 1990; Russell and Herschlag 1999a). Reaction aliquots were removed at specified times to be quenched with 2 vol of a solution containing 20 mM EDTA and 85% formamide. Radiolabeled oli-gonucleotides were separated by denaturing gel electrophoresis (7 M urea, 20% acrylamide) and quantitated using PhosphorImager analysis (Molecular Dynamics) with ImageQuant quantitation software. For slow reactions, rate constants were obtained from initial rates assuming endpoints of 95%. All other reactions were followed to completion, and good first-order fits to the data with endpoints of ≥90% were obtained in all cases (R^{2 ≥}0.98) (Kaleidagraph, Synergy Software).

Measurement of (k_cat/K_m)^(AUC)G and (k_cat/K_m)^(AUC)GA values

(k_cat/K_m)^G values were determined with three subsaturating concentrations of G and E saturating with respect to S (2–20 μM G, 0.5–2 μM G for the (C₁₁₁·G₂₀₉)·C₃₀₅ mutant, 70 nM E). Rate constants were plotted as a function of G concentration to yield (k_cat/K_m)^G from the slope. (k_cat/K_m)^AUCG values were determined analogously using 0.05–0.2 μM AUCG for wild-type ribozyme, or 0.2–1 μM for the C₃₀₅ mutant, 0.4–2 μM for the (C₁₁₁·G₂₀₉) mutant, and 0.04–0.06 μM AUCG for the (C₁₁₁·G₂₀₉)·C₃₀₅ mutant. In all cases, the −1d,rSA substrate was used to ensure that the chemical step was rate limiting.

(k_cat/K_m)^GA measurements were performed using 5–20 μM GA (K_d ≈ 1 mM) (Bevilacqua et al. 1996; data not shown) and E saturating with respect to P (70 nM E). Rate constants were plotted as above. (k_cat/K_m)^AUCGA measurements were performed analogously using 1–4 μM AUCGA. The 5′-exon analog −1d,rP was used in these experiments to ensure that the chemical step remained rate limiting under all conditions.

Measurement of G and AUCG affinities

To determine the affinities of ribozyme complexes for G or AUCG, the rate constant for reaction of *S was determined as a function of G (or AUCG) concentration using concentrations of G (or AUCG) ranging from 10-fold below to 10-fold above the K_d. The ribozyme concentration was 25 nM to ensure that S was fully bound to the ribozyme. The observed rate constant for cleavage of *S was plotted as a function of G concentration and fit to Equation 2.

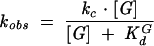(2)

The −1d,rSA (or −1d,rSA₅ in the case of G) was used in these experiments to ensure that the chemical step was rate limiting and that the observed K^G_1/2 equals the K^G_d (McConnell et al. 1993). To determine the K^G_d in the open complex, a substrate with a 2′-methoxy substitution at position −3 was used (Narlikar and Herschlag 1996; Bartley et al. 2003) with 50 nM ribozyme.

The affinity of AUCGA for the E·P complex was determined analogously using −1d,rP and AUCGA concentrations ranging from 10-fold below to 10-fold above the K_d value with ribozyme saturating with respect to P [25 nM; K_d = 0.01 – 1 nM for wild-type and mutant ribozymes (Table 2 ▶)].

Dissociation constants for S and P

Because binding of S and P is very tight, it was not possible to measure dissociation constants for S and P by varying ribozyme concentration. This is because at ribozyme concentrations sufficiently low to be subsaturating, nonspecific losses to the tube walls occur (Karbstein et al. 2002). Equilibrium dissociation constants for S and P were instead calculated from dissociation rate constants and the association rate constant of ~10⁸ M⁻¹ min⁻¹ that appears to hold for binding of all oligonucleotide substrates under a range of conditions (Herschlag and Cech 1990; Knitt et al. 1994; Karbstein et al. 2002).

The dissociation rate constants for S (or P) from E·S (or E·P) were obtained in pulse-chase gel-shift experiments (Mei and Herschlag 1996; Karbstein et al. 2002). Trace *S (or *P) was bound to saturating amounts of ribozyme (120 nM) and a large excess of unlabeled P (>10-fold over ribozyme) was then added. At specified times, aliquots were loaded onto a running native gel in THEM buffer (33 mM Tris, 67 mM HEPES, 1 mM EDTA, 10 mM MgCl₂). The remaining fraction of bound oligonucleotide was plotted against the time of the chase and fit to an exponential decay. Control experiments confirmed the efficiency of the chase and full binding prior to addition of the chase.

Calculations for the free-energy profile in Figure 3 ▶

Free energies were calculated from equilibrium constants K or from rate constants k at 30°C and a standard state of 1 mM G and GA according to Equations 3 and 4,

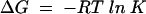(3)

(4)

where R is the Boltzmann constant, T = 303 K and ν = 6.212·10¹² s⁻¹. Table 6 ▶ lists the rate and equilibrium constants and their sources used to calculate the free energy profile.

TABLE 6.

Rate and equilibrium constants used to calculate the free energy profile in Figure 3 ▶

Constant	Wild type	C111 · G209	Reference
Kdocks,S	22	0.07a	Bartley et al. 2003
kdock,S (min−1)	162	162b	Bartley et al. 2003
Kd,G (μM)	128	220	Table 3 ▶
kon,G (M−1 min−1)	6 · 105	6 · 105	Karbstein and Herschlag 2003
Keq	0.7	0.7	K. Karbstein and D. Herschlag, unpubl. data
kc (min−1)	0.03	0.03c	Table 2 ▶
Kd,GA (mM)	1d	1d	Data not shown
kon,GA (M−1 min−1)	6 · 105	6 · 105	Karbstein and Herschlag 2003
Kdock,P	880	2.8e	Narlikar et al. 1995
kdock,P (min−1)	162b	162b	Bartley et al. 2003

^aThis value for K_dock was calculated from the 28-fold reduction in (k_cat/K_m)^G and the twofold weaker G binding for this mutant, assuming that the rate constant for the chemical step was unaffected.

^bMany substitutions have been shown to affect K_dock through k_undock but not k_dock; we therefore assume that k_dock,S remains un-affected (Bartley et al. 2003).

^cThe lower observed rate constant for reaction of the E · S · G ternary complex is due to unfavorable docking and not to a lower intrinsic reaction rate constant (See “A Threshold Model to Explain the Different Effects of Triplet Disruption on the First and Second Step of Self-splicing”).

^dAs GA binding is weak (K_d > 1 mM, Bevilacqua et al. 1996 and data not shown), this value could not be reliably measured. However, the value of 1 mM, is obtained from the affinity of UCG to E · P of 88 μM and the 14-fold stronger binding of UCG than G (Karbstein et al., 2002).

^eCalculated from K_dock,_S and the 40-fold stronger docking of P relative to S (Narlikar et al. 1995).

Calculations of the effects on docking from the mutations in Table 5 ▶

K^S_mut represents the amount by which the docking equilibrium is destabilized by the mutant construct relative to the wild-type construct (Eq. 5).

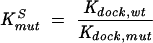(5)

K_dock,mut and K_dock,wt represent the equilibrium constant for docking for the mutant and wild-type ribozymes, respectively. The value for K_dock,wt of 22 was obtained from Bartley et al. (2003),and the value for K_dock,mut was obtained from Equation 6, which was derived with the assumptions that the wild-type and mutant ribozymes have the same reaction rate from their closed complexes and that the wild-type rate constant, but not the mutant-rate constant, is that for the fully docked case; this latter approximation does not significantly affect the calculated values for mutants, such as those herein, in which docking is substantially destabilized. k_c,mut is the observed rate constant of cleavage by the mutant ribozyme with saturating substrates (G and −1d,rSA) and k_c,wt is the corresponding rate constant for cleavage by the wild-type ribozyme.

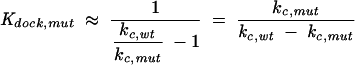(6)

Abbreviations

• S, 5′-splice site analog without specifying the identity of the 2′-substituents, which can be a hydrogen atom, a hydroxyl group, or a methoxy group (see Chart 1 ▶ for the specific oligonucleotides used)

• P, 5′-exon analog (see Chart 1 ▶)

• *S, radioactively labeled S

• *P, radioactively labeled P

• G, guanosine

• E, L-21 ScaI ribozyme (mutant or wild type)

• HPLC, high pressure liquid chromatography

• HEPES, 4-(2-hydroxy-ethyl)-piperazine-1-ethane-sulfonic acid

• MOPS, 3-(N-morpholino)-propane-sulfonic acid

• EDTA, ethylenediaminetetraacetic acid, Tris, Tris[hydroxymethyl]aminomethane

• IGS, internal guide sequence