On the critical radius in generalized Ostwald ripening

Abstract

The relation between the critical radius and the particle size distribution for generalized Ostwald type ripening processes whereby the mass transfer coefficient is modelled by a power law was derived. The critical radius is determined by the growth rate, the mass transfer coefficient and the mass balance, and is independent of whether the limiting stationary growth regime has been obtained.

INTRODUCTION

A polydisperse precipitate produced by nucleation in a metastable supersaturated solution is far from thermodynamic equilibrium, i.e. a state of minimal free energy. A decrease of free energy is accomplished by a coarsening of the precipitate which essentially reduces the surface free energy with respect to the surrounding solution. The process is called Ostwald ripening and is a direct consequence of the Kelvin effect (Adamson and Gast, 1997), that is the higher solubility of small particles, which quantitatively is expressed as follows:

C(r)=C(∞)exp(α/r) (1)

where, C(r) is the solubility of a dispersed phase particle with radius r. The bulk solubility C(∞) corresponds to the solubility of a particle with infinite radius, i.e., to the solubility of the dispersed phase when it has a flat surface or bulk solubility. α is called the capillary length and is given by

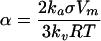where, V _m is the molar volume of the dispersed phase, σ is the interfacial tension, R is the universal gas constant, T is the absolute temperature and k _a and k _v are the area and volume shape factors.

Due to the size-dependent solubility there will be transport of monomers from smaller to bigger particles which grow at the expense of the former. There should be a critical radius r _c. When r>r _c the number of molecules in a particle increases, that is, the particle grows. If r<r _c, the particle shrinks (Kahlweit, 1970). Since the Ostwald ripening process is determined by the value of the critical radius r _c and since the critical radius cannot be directly measured experimentally, the question of how to determine the critical radius arises.

Lifshitz and Slyozov (1961) and independently Wagner (1961) studied the long-time regime of Ostwald ripening using several assumptions, such as negligible volume fraction and diffusion-controlled growth without convection, and drew the conclusion that the critical radius r _c is equal to the number-average radius r _N of the limiting self-similar size distribution. Note that the limiting self-similar size distribution is skewed with a tail towards the smaller particle sizes and predicts that no particles with sizes larger than 1.5 times the average size are present. Such a distribution is however not realistic for many freshly prepared dispersions or emulsions. For such systems the size distribution is skewed with a tail towards the larger particle sizes and substantial fraction of particles with sizes larger than 1.5r _N are commonly present. It had also been shown by simulation (Smet et al., 1997) that the transition from the initial size distribution to the limiting one is a long lasting process due to the initial presence of particles with sizes larger than 1.5r _N.

In this sense, the Ostwald ripening process is determined by the value of the critical radius r _c that unfortunately cannot be measured experimentally. During the course of ripening, the particle size distribution is easy to measure. The question of what is the relation between r _c and the particle size distribution for more generalized Ostwald ripening arises.

Finsy (2004) showed that when single internal phase molecules are transported by molecular diffusion from one particle to another the critical radius r _c equals the number average size whatever the form of the size distribution. However there are processes whereby the transport is different from molecular diffusion in which case the critical radius is different from the number average radius and should be identified. In this contribution we present the relation between the critical radius and the particle size distribution for the case of Ostwald ripening whereby the mass transfer coefficient is modelled by a power law of the particle size.

DETERMINATION OF r _c FROM THE PARTICLE SIZE DISTRIBUTION

In this treatment of Ostwald ripening the growth rate of a particle is given by a mass transfer equation. In particular, the increase of number of molecules n of a particle with radius r is given by

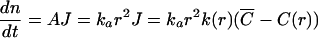(2)

where A is the interfacial area of the particle, J is the flux of a molecularly dispersed material, and k(r) is the size-dependent mass transfer coefficient. In the Ostwald ripening, the concentration of the internal phase molecules in the external phase can be assumed to be constant throughout the system. All particles are surrounded by the same concentration of internal phase molecules C¯ at a distance from the particle surface equal to their own radius. Obviously, when C¯=C(r), the particle will not grow nor shrink. Hence, the critical radius r _c satisfies the relation C(r _c)=C̄. Using Eq.(1) to relate the solubility to the particle size yields

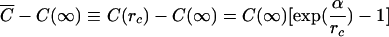(3)

In the case α<<r and α<<r _c, the exponential factor in Eq.(1) and Eq.(3) can be approximated by the two first terms of its Taylor series (Kahlweit, 1970). That way, Eq.(2) becomes

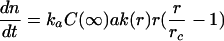(4)

The number of molecules in a particle with radius r is given by

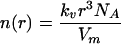(5)

where N _A is Avogadro’s number. Using Eq.(5), Eq.(4) may be rewritten as

(6)

As summarized by Vengrenovitch (1982), when generalizing the available data one can model the size-dependent mass transfer coefficient k(r) of an individual particle for different Ostwald ripening mechanism as

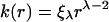where ξ_λ is a size-independent constant. For λ=2, particle growth will be controlled by the rate of reaction on its surface. For diffusion controlled growth, λ=1. If the Ostwald ripening process is limited by diffusion of atoms along the grain boundary, λ=0 and for λ=−1, the supply of material to particles is along dislocation pipes of the cross section.

Introducing a new variable

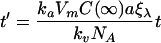(7)

simplifies the notation of Eq.(6) to

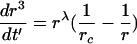(8)

The increase of the particles with size larger than r _c occurs at the expense of the decrease of particles with sizes smaller than r _c.

Note that the material balance includes, in principle, the dissolved particulate material in the continuous phase. However in most practical cases the amount of dissolved material is negligible compared to the amount present in the particles. Hence for a discrete set of N particles with radii r_i

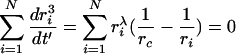(9)

yielding

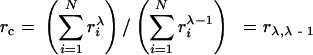(10)

In case of a continuous distribution W of particle radii, Eq.(10) becomes

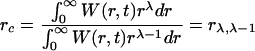(11)

In the case of particle growth controlled by the rate of reaction on its surface, λ=2. In this case the mass transfer coefficient k(r) is independent of the size. That is λ=2 (Vengrenovitch, 1982) and the critical radius r _c equals r _L, the particle length average radius.

In case the mass transfer rate is determined in the first place by the diffusion of molecules through the particle interface, λ=1 (Vengrenovitch, 1982) and the critical radius r _c is equal to r _N, just as for the case of molecular diffusion (Finsy, 2004).

If the Ostwald ripening process is limited by diffusion of atoms along the grain boundary, λ=0. If the supply of material to particles is along the cross section dislocation pipes, λ=−1 (Vengrenovitch, 1982). In these two Ostwald mechanisms the critical radius r _c can be determined from the experimental particle size distribution by Eq.(10) or Eq.(11).

In other cases, when the size dependence of the mass transfer coefficient is known, the critical radius r _c can be determined from the experimental particle size distribution by Eq.(10) or Eq.(11).

So, as long as the mass of dispersed material is conserved, the critical radius in the Ostwald ripening process can be determined from the particle size distribution at any instant of the ripening process.