Continuous Photobleaching in Vesicles and Living Cells: A Measure of Diffusion and Compartmentation

Abstract

We present a comprehensive and analytical treatment of continuous photobleaching in a compartment, under single photon excitation. In the very short time regime (t < 0.1 ms), the diffusion does not play any role. After a transition (or short time regime), one enters in the long time regime (t > 0.1–5 s), for which the diffusion and the photobleaching balance each other. In this long time regime, the diffusion is either fast (i.e., the photobleaching probability of a molecule diffusing through the laser beam is low) so that the photobleaching rate is independent of the diffusion constant and dependent only of the laser power, or the diffusion is slow (i.e., the photobleaching probability is high) and the photobleaching rate is mainly dependent on the diffusion constant. We illustrate our theory by using giant unilamellar vesicles ranging from ∼10 to 100 μm in diameter, loaded with molecules of various diffusion constants (from 20 to 300 μm²/s) and various photobleaching cross sections, illuminated under laser powers between 3 and 100 μW. We also demonstrated that information about compartmentation can be obtained by this method in living cells expressing enhanced green fluorescent proteins or that were loaded with small FITC-dextrans. Our quantitative approach shows that molecules freely diffusing in a cellular compartment do experience a continuous photobleaching. We provide a generic theoretical framework that should be taken into account when studying, under confocal microscopy, molecular interactions, permeability, etc.

INTRODUCTION

Recent advances in microscopy and in fluorescent protein tags make it possible to characterize the dynamics of proteins and organelles in living cells. The corresponding techniques and methodologies can put into evidence the highly organized cell nucleus (1,2), the reality of the membrane microdomains (3–7), and the dynamics of many proteins through the cell or a compartment (8–10). Macromolecular mobility depends not only on diffusion and active transport, but also on specific and nonspecific interactions, compartments, and molecular crowding (8,11). Recently, fluorescence recovery after photobleaching (FRAP) experiments became well designed to explore binding interactions in living cells (12,13). In this kind of experiment, an initial intense laser shot brings the system out of equilibrium by locally depleting the concentration of fluorescent molecules; then the relaxation of the depleted region toward the equilibrium (the fluorescence recovery) can be analyzed in terms of diffusion and interactions with binding sites. A method related to FRAP is fluorescence loss in photobleaching (FLIP) (14), where the variations of fluorescence outside the illuminated zone are monitored to give information about compartmentation (15). In contrast to FRAP and FLIP techniques that use an instantaneous and intense illumination followed by a less intense illumination, Peters et al. (16) introduced in the 1980s the so-called continuous fluorescence microphotolysis and applied it to lateral two-dimensional diffusion in membranes (16) and later on in three-dimensional diffusion (17), that consists in analyzing the fluorescence decay versus the mobility, size, and topology of the reservoir of intact fluorophores. Recently, it was shown that diffusion and binding of molecules to specific sites could be measured by combining continuous fluorescence photobleaching (i.e., continuous fluorescence microphotolysis), fluorescence correlation spectroscopy (FCS), and confocal laser scanning microscopy (CLSM) (18). The advantage introduced by combining continuous fluorescence microphotolysis with FCS is that the latter gives the density number and, especially, the mobility of the “fast-enough” involved species. In the work quoted above (18), the FCS measurements were recorded after bleaching, with a reduced laser power to avoid photobleaching. We recently showed that FCS analysis can be directly performed on the photon count stream recorded during the photobleaching process, provided that an adapted procedure is applied to correct the bias of the autocorrelation function produced by the intensity decay (19). In this previous work, we also began an investigation of the relation between the photobleaching rate of a molecule crossing the laser beam, the fluorescence intensity decay, and the size of the compartment of interest, by using giant unilamellar vesicles. However, we had not considered the case of very slow diffusion (or strong photobleaching), such that the photobleaching probability of a molecule crossing the beam is high. In addition, at that time, we did not try to correlate the sizes of the compartments of the living cells with the fluorescence intensity decay rates.

We stress the fact that, to our knowledge, no methodology, based on the photobleaching phenomenon, has been proposed so far that allows one to measure the size of three-dimensional intracellular compartments at the scale of 10 μm. As a matter of fact, the goal of the work of Wachsmuth et al. (18) is to obtain bound fractions and/or dissociation rates or residence times at binding sites (in contrast with our work, where the fluorescent molecules are freely diffusing within compartments). FRAP experiments can be sensitive to the geometry of the environment (20), but they are not devoted to the evaluation of the size of the intracellular compartments; FLIP experiments are designed to characterize the compartmentation, but this technique is generally applied in a semiquantitative way (15). Finally, no study up to now, to our knowledge, quantifies the continuous fluorescence decay of a pool of molecules, freely diffusing in a cellular compartment of the order of 10 μm.

In this work, we expand our initial approach by studying the relation between the size of the compartment, the diffusion constant of the fluorescent molecules, the laser power and the photobleaching rate, over almost four orders of magnitude of the control parameters. To validate our theoretical approach, we use giant unilamellar vesicles, the diameter of which ranges from 10 to 100 μm. As a result, we show that the combination of the FCS data (in terms of diffusion constant) and of the fluorescence decay time makes it possible to get information about the size of the region where the molecules are compartmented. We emphasize the fact that, in our case of relatively large compartments, the autocorrelation function is not compartmentation-dependent. This must be contrasted with much smaller compartments such as the dendrites of neurones (21), where it has been shown that the autocorrelation function depends upon the compartment size. We applied our methodology to living cells, either loaded with FITC-dextran molecules or transfected with enhanced green fluorescent proteins (eGFP). We observed that, despite the fact that these cells have quite similar sizes, they lead to significantly different fluorescence decay times for FITC-dextran and eGFP. We attribute this difference to the lower permeability of the nuclear envelope to eGFP than to the small FITC-dextran molecules (MW = 4300).

In the next section, we detail the Materials and Methods (experimental and numerical). In Model, we introduce the model developed to interpret the experimental data; apart from the first subsection, the reader may skip this rather technical section to go directly to the corresponding numerical results given in Results of Simulations. The Experimental Results (concerning vesicles and cells) are then given, followed by Discussion and Conclusion.

MATERIALS AND METHODS

Experimental methods

CLSM-FCS system

FCS measurements were performed on a single photon CLSM-FCS confocal microscope system (Confocor 2, Zeiss, Jena, Germany) using a 40× water immersion objective lens (C-Apochromat, 1.2 NA, Zeiss) and high sensitivity avalanche photodiodes. The values of the laser power used for the experiment were measured with a calibrated photodiode immersed in a drop of water covering the front pupil of the objective lens. These values range from 2.6 μW to 103 μW. All experiments were performed with the Ar⁺ line at 488 nm.

Preparation of giant unilamellar vesicles

Giant phospholipidic vesicles were swollen from L-a dioleoyl-phosphatidylcholine using the electroformation method (22). They were prepared in sucrose solutions (typically 40 mM) containing one of the following molecules with a concentration of ∼20 nM: Fluorescein-5- isothiocyanate (FITC, MW = 389.38), FITC-dextran FD4, FD70, and FD250S (MW = 4300, 68,100, and 282,000) from Sigma (St. Louis, MO); fluorescein (MW = 332.31) and streptavidin fluorescein conjugate (MW = 53132) from Molecular Probes (Eugene, OR); or purified recombinant eGFP proteins from Clontech (Palo Alto, CA). The giant vesicles (typically 10–100 μm) were then diluted in glucose solutions of equal osmolalities, to deposit on the bottom of the perfusion chamber, where they could be observed. The concentration of fluorescent molecules within the vesicles could be significantly different from that in the solution (especially FITC-dextran), due to the preparation method.

Preparation of cells

Hela cells were cultured in Dulbecco's modified Eagle's medium supplemented with 10% fetal calf serum in 5% CO₂ atmosphere at 37°C. Cells were plated on a Lab-Tek chambered cover glass (Nunc, Roskilde, Denmark). FITC-dextran FD4 was loaded into cells using influx Pinocytic cell-loading reagent (Molecular Probes). Enhanced green fluorescent protein (eGFP) was expressed in cells that were transfected using Polyfect transfection reagent (Qiagen, Hilden, Germany). Living cells were measured in HBSS (+ CA²⁺, + Mg²⁺) medium buffered with HEPES at 37°C.

Processing of experimental data

Image analysis

The radii of the vesicles were straightforwardly measured with the Zeiss LSM 510 image software. Cells were measured using an image analysis software (METAMORPH offline, Molecular Devices, Sunnyvale, CA). The areas of the cells and of the nuclei, A, were measured and the equivalent disc radii, R (A = πR²), were calculated.

Fluorescence decay fitting

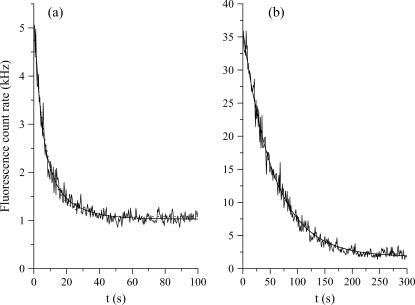
The fluorescence intensity decays were recorded during 30–300 s (depending on the vesicle size, laser power, and molecule) by centering the vesicles or the cell nuclei on the laser waist. The fits were performed by excluding the first part of the decays during which the diffusion settles through the whole compartment. This transition toward a quasi-stationary regime (see Model, and Results of Simulations, for further details) takes a time of the order of τ_R = R²/4D, where D is the diffusion constant. For instance, a vesicle with a radius R ≅ 20 μm gives τ_R ≅ 0.4 s for FITC (the smallest molecule used in this work, D = 280 μm²/s) and τ_R = 5 s for FITC-dextran FD250S (the largest molecule used in this work, D = 19 μm²/s). However, the long time exponential decays were fit with single exponentials for eGFP in vesicles but, for the other cases, with bi-exponentials (see Fig. 1),

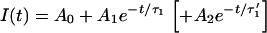(1)

FIGURE 1.

Fluorescence decays of FITC-dextran FD70 (a) and of eGFP (b) in two vesicles of similar radii (≅11.5 μm). In both cases the laser power is 13 μW. The bi-exponential fit of FD70 (solid line) gives the decay times τ₁ = 4.2 s and τ₁′ = 14.1 s (the result of a mono-exponential fit, represented by the dotted line, is τ₁ = 7.7 s), while the mono-exponential fit (solid line) of eGFP gives τ₁ = 56 s.

When two exponentials were necessary to fit the long-time exponential decay, the shorter time, τ₁, was assumed to be characteristic of the compartment size (and therefore to follow Eq. 2a, see below), whereas the additional very long time, τ₁′, was attributed to aggregates, membrane interactions, or permeability (for instance, FITC was observed to pass the membranes). We stress the fact that the two characteristic times, τ₁ and τ₁′, cannot reflect the transition toward the quasi-stationary regime (see Model, below), because the shorter of these two times is already longer than the time for the quasi-stationary regime to settle, τ_R. For example, the vesicle of Fig. 1 a, loaded with FD70, has a diameter of ∼11.5 μm, which corresponds to τ_R ≅ 0.7 s. This time is much smaller than τ₁ (4.2 s) and of course, than τ₁′ (14.1 s). Note that analogous double-exponential behaviors have already been reported (23). Henceforth τ₁′ was excluded from the analysis of the vesicle decays because our goal is to validate our model for compartmentation and photobleaching. Conversely, the effects of permeability will be explicitly discussed when dealing with live cells.

From time decays to compartment size

To analyze the experimental data, the dimensionless master equation of the long time regime (see Eq. 15) can be written in terms of compartment radius R in μm, decay time τ₁ in s, diffusion constant D in μm²/s, and laser power P (assumed to be known) in photons per s and photobleaching cross section σ_B in μm²:

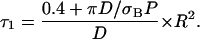(2a)

Thanks to this equation, the measurement of τ₁ allows one either to determine the photobleaching cross sections when the diffusion constant and the size of the compartment are known, or to get information about compartmentation when the diffusion constant and the photobleaching cross section are known. When πD ≫ σ_BP, one is in the fast diffusion limit of Eq. 2a:

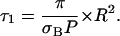(2b)

This equation was already given in our previous article (19), with a slightly different numerical factor (2.5 instead of π), due to approximations that were not exactly the same. It is worthwhile to note that in Eq. 2b the diffusion constant disappears from the relation between τ₁, σ_B, and R. This may be convenient to interpret the experimental data, providing one can ascertain the validity of the fast diffusion limit.

FCS analysis

The autocorrelation curves were calculated, from the raw data set, using homemade programs developed in a C++ environment (Microsoft Visual C++). These programs make it possible to correct the raw data from the photobleaching effect, before calculating the autocorrelation. For that purpose, two equivalent methods can been applied: one can either divide the photocount stream into short and equal time slices, or rectify the raw data to give a count rate that becomes constant on average (19). The autocorrelation curves were then fit with the standard formula used for three-dimensional translational diffusion, in presence of a triplet dynamics; that is,

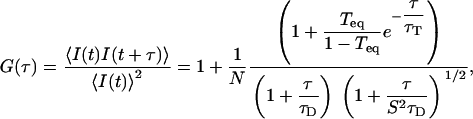(3)

where N is the number of molecules in the confocal volume, T_eq is the fraction of molecules in the triplet state, τ_T is the characteristic triplet time, τ_D is the diffusion time, and S is the structure parameter (24).

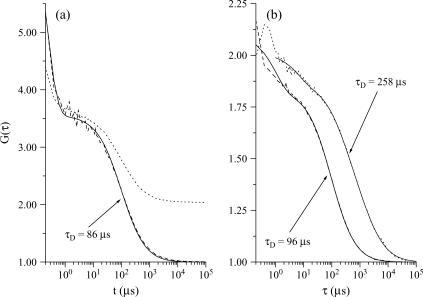
The diffusion constants of the various molecules used in this article have therefore been measured by FCS (in solution, vesicles, or cells) and are reported in Table 1. Fig. 2 shows an example of such FCS measurements for eGFP.

TABLE 1.

Diffusion constants

	Literature	Solution	Vesicles	Cells
FITC	—	280 ± 5 μm2/s	280 ± 5 μm2/s	—
Fluorescein	—	280 ± 5 μm2/s	280 ± 5 μm2/s	—
Strep-fluo.	60 μm2/s*	¶	73 ± 15 μm2/s	—
	74 μm2/s*
FD4	173 μm2/s†‖	143 ± 7 μm2/s	173 ± 20 μm2/s	26 ± 4 μm2/s
FD70	40,2 μm2/s†	33 ± 3 μm2/s	47 ± 10 μm2/s	—
FD250S	19 μm2/s†	24 ± 5 μm2/s	26 ± 2 μm2/s	—
eGFP	78 μm2/s in sol.‡	70 ± 7 μm2/s	90 ± 10 μm2/s	21 ± 4 μm2/s
	25 μm2/s in cyto.‡
	33 μm2/s in nuc.§

Mean values and SD of the diffusion constants of the molecules used in this work are defined below.

^*(34).

^†Calculated from the molecular weight (35).

^‡(36).

^§(37).

^¶Aggregation and /or important triplet population prevent a reliable determination of the diffusion constant.

^‖Small dextran molecules (MW = 70 × 10³) have been found to be approximately seven times slower in nucleus than in water solution (37).

FIGURE 2.

Autocorrelation curves of eGFP fluorescence signals and their corresponding fits (solid lines), the diffusion times of which are given in the figure. Panel a corresponds to the data of the vesicle plotted in Fig. 1 b, before correction of the fluorescence decay (dotted line) and after correction (dashed line). Panel b shows a comparison between the autocorrelation obtained in solution (dashed line) and in a cell, after correction (dotted line). The amplitude of the autocorrelation function of eGFP in cell has been multiplied by a factor 20 for convenience; in addition, a slow component (τ_D = 1566 μs) had to be added to perform a satisfactory fit, up to very long times. In all cases the laser power is 13 μW.

Numerical calculations

To solve numerically the general equation of diffusion and reaction within an impermeable compartment (see Eq. 7), it is interesting to work with a cylindrical compartment, oriented and centered along the laser beam that induces the photobleaching reaction. The waist and the Rayleigh distance of this Gaussian beam are fixed to ω₀ = 0.25 μm and z_R = 0.5 μm (see Eqs. 7a and 7b). Taking advantage of the rotational invariance, the diffusion-reaction equation can be written as

(4)

where the notation Δ_r,z represents the two-dimensional Laplacian ∂²/∂r² + ∂²/∂z². In addition, the integration domain is then reduced to a square section, defined by −R < r < R and −R < z < R, of the cylinder containing the axis. The boundary conditions at the edge of the compartment are fixed by mass conservation: the mass flux has to cancel at the boundary, which implies that the gradient of C vanishes at the edges of the domain. Thanks to the symmetries of the problem (invariance through r → −r and z → −z), the cancellation of the flux at the boundaries is equivalent to periodic boundary conditions on the square domain. The diffusion-reaction Eq. 7 can then be solved in the Fourier space. If k corresponds to a wave-vector, Eq. 13 can be written in a discrete form as

(5)

where index k stands for a Fourier transformation, k² is the square of the modulus of k, and t is the time at which the quantity is evaluated. Note that we evaluate the Laplacian in the right-hand term of Eq. 5 at time t+dt, which corresponds in fact to an implicit scheme ensuring a better convergence of the method. The solution can then be easily obtained from an initial guess of the concentration field C(r, z) (in practice a homogeneous system), by iterating the relation

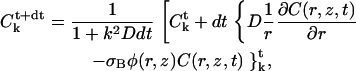(6)

where the nonlinear term between braces has to be estimated in the direct space at each time step and Fourier-transformed to obtain the new estimate 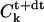that has to be transformed back to obtain C(r, z, t+dt). Due to the presence of the factor 1/r, inducing an artificial singularity along the axis if care is not taken, we extrapolate the quantity 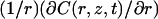to estimate its value at r = 0. We use in practice a square mesh to discretize the square domain, the number of points depending on the radius of the compartment: for a 10-μm compartment, we use 200 × 200 grid points, while a 30-μm compartment requires 600 × 600 grid points to keep a comparable resolution. The time step can be varied from 10⁻³ times the diffusion time, to 10⁻⁶ (depending again on the requested precision). To compare with experiments, fluorescence can be estimated by an integration of C(r, z, t) in a small cylindrical region, providing the number of fluorescent molecules in the confocal volume, N_CV. Please note that in practice, this cylinder is much smaller than the compartment itself, since the measurement cylinder has a diameter of 0.5 μm, for a height of 2.5 μm, while the compartment radius goes from 10 to 30 μm.

MODEL

Interplays of diffusion, compartmentation, and photobleaching

To get some order of magnitude about photobleaching encountered during FCS experiments, let us consider the case of molecules, tagged with fluorescein and contained within a cylindrical compartment of radius R = 10 μm. Illuminated by a laser beam of a few tens of μW, these molecules will experience a local photobleaching rate, K₀, at the laser beam waist (ω₀ ≅ 0.2 μm), of the order of 1 kHz (28). The photobleaching rate of the ensemble of molecules within the compartment is obtained by multiplying the previous local rate, K₀, by the probability of any molecule to be shined by the laser beam; that is, by 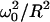(assuming a rod-shaped laser beam of radius ω₀). This leads to a global photobleaching decay rate, K₀ × slightly smaller than 1 s⁻¹. This result is independent of the diffusion constant, D, because it has been derived by implicitly assuming that the photobleaching probability of a molecule diffusing through the laser beam is very small. This corresponds to a weak local photobleaching rate, or to a fast diffusion. In this situation, the concentration of fluorescent molecules can be considered as being homogeneous everywhere within the compartment, even at the laser beam. On the contrary, when each molecule systematically photobleaches when crossing the laser beam, because it diffuses slowly or because the local photobleaching rate is strong, there is a significant depletion of fluorescent molecules in the irradiated zone. In that case, the global photobleaching rate is the inverse of the time it takes for the molecules of the compartment to reach, by diffusion, the hole in fluorescence, that is, D/R². It is worth noting that, in both cases, the photobleaching rate decreases with the squared radius of the compartment. This is related to the fact that photobleaching under single photon excitation has almost a two-dimensional geometry, in contrast to photobleaching under two-photon excitation (25).

From the above discussion one immediately sees that a possible set of relevant parameters is the radius, R, of the compartment; the diffusion constant, D; the photobleaching rate, K₀, at the laser beam waist; and the size of the beam waist, ω₀. Hereafter, the three last parameters will be compacted in one dimensionless parameter, the value of which is an indicator of whether the photobleaching is strong or weak (i.e., the diffusion is slow or fast). Finally, we emphasize the fact that the establishment of the two different regimes discussed above (slow versus fast diffusion or strong versus weak photobleaching) needs some time. As a matter of fact, at very short times (that is, as long as the diffusion through the laser beam waist is negligible), the fluorescence decay occurs at the rate K₀. The transition toward the quasi-stationary regime will be discussed in the presentation of the numerical simulations in Results of Simulations. Here, below, we present the mathematical theory underlying our model of diffusion-reaction in a compartment.

General equations

Let us consider the diffusion equation in the presence of a first-order irreversible chemical reaction induced by the laser field,

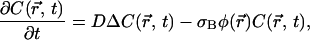(7a)

where is the concentration of fluorescent molecules at point 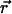and time t, D is the diffusion constant, σ_B is the photobleaching cross section, and 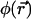is the laser intensity at point 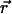(in units of photon.s⁻¹.m⁻²). This equation is valid anywhere within the compartment of radius R, at any time. At the initial time, when the laser is switched on, the concentration is homogeneous in the compartment, i.e., ; afterwards a hole in fluorescence develops in and around the illuminated region. If the walls of the compartment are impermeable, the additional boundary condition is

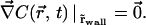(7b)

At places where the local photobleaching rate (in units of s⁻¹), 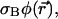is negligible, Eq. 7a reduced to the usual diffusion equation. Assuming that the laser intensity corresponds to the usual Gaussian beam, 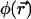is given by

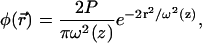(8a)

(8b)

where r represents the radial coordinate and z the coordinate along the axis, P is the laser power (in units of photon s⁻¹), ω₀ is the laser waist (fixed to 0.25 μm) in the focal plane of the objective, and z_R is the Rayleigh distance (fixed to 0.5 μm).

Heuristic approach

Hereafter we are interested in giving an approximated solution for the fluorescence decay observed at long times. Therefore, before solving numerically the full system of Eqs. 7 and 8, two limiting cases can be considered: the fast and the slow diffusion regimes. To better investigate the dynamical behavior in these two regimes, Eq. 7a can better be rewritten in dimensionless units as

(9)

with

(10a)

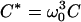(10b)

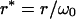(10c)

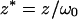(10d)

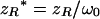(10e)

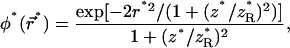(10f)

where Δ* is the Laplacian in dimensionless units and D* controls the competition between diffusion and photobleaching,

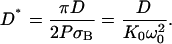(11)

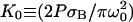is the photobleaching frequency at the laser beam waist. In our previous article (19), we had introduced the photobleaching parameter, p_B = σ_BP/D, instead of D*. The characteristic time appearing in Eq. 10a, is the time for a molecule to diffuse across the beam waist. The choice of ω₀ as the unit of length (Eqs. 10b–10e) is sensible since it defines the width of the region where the photobleaching frequency is the fastest. The control parameter D* is simply the ratio between the characteristic times of two processes occurring at the laser waist: the local photobleaching time 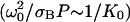and the diffusion time 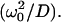D* can be viewed as a dimensionless diffusion coefficient. The two limiting regimes are easily identified from Eq. 9, as detailed below.

The fast diffusion regime, which corresponds to D* ≫ 1

In this regime we can thus expect the concentration profile 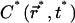to remain homogeneous in the system at any time t*, since the diffusion is instantaneous at the timescale of photobleaching. The decay of C*(t*) is obtained by first integrating Eq. 9 over the whole volume of the compartment. This has the advantage to remove the diffusion contribution without any approximation, thanks to the absence of matter flux at the boundaries. If N* denotes the number of fluorescent molecules in the container, 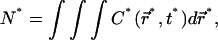the volume integration of Eq. 9 leads to

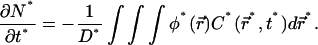(12a)

Assuming that the concentration profile is nearly homogeneous, the integral term in Eq. 12a simply rewrites as

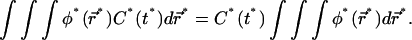(12b)

In practice, since the radius of the compartment R* is very large (the size of the compartment is much larger than the waist of the beam), the integral of φ* can be extended to R* → +∞. This assumption is not strictly valid in the whole container when the beam is highly focalized. In such a case, the integral of φ* should keep a weak dependence in R*. Since this dependence is not visible in our data, we shall neglect it in this heuristic approach and assume R* → ∞. Modeling the compartment with a cylinder of radius R* and height h*, the integral term in Eq. 12b becomes

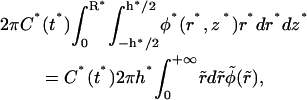(12c)

where and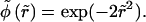

Taking into account the fact that N* = πR*² h * C* (t*) and that the integral of the right-hand side of Eq. 12c equals ¼, Eqs. 12a and Eqs. 12c lead to

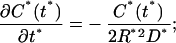(13)

that is,

(14)

where we identify the decay time t*_decay ≅ 2D R*².

The slow diffusion regime, which corresponds to D* ≪ 1

In such a case, a deep hole in fluorescence should be produced very rapidly at the center of the laser beam, and the long time relaxation of the fluorescence signal at the center should be dominated by the slow diffusion of the molecules across the cylinder. We thus expect the decay time to be given by t_decay ≅ R²/D and thus, in dimensionless units t*_decay ≅ R*².

From the above discussion, it is tempting to conjecture a general dependence of the form

(15)

where A is a constant and B is expected to be equal to 2 after Eq. 14.

Two-dimensional approximation

We have already noted that photobleaching under single photon excitation is mainly a two-dimensional problem. This is related to the fact that the product of the diffusion time through the laser beam, ∼ω²(z)/D, by the mean laser intensity, ∼P/ω²(z), is independent of the axial position, z. This makes it possible to apply the theory of Sturm-Liouville equations (26) in a two-dimensional approximation, which is both meaningful and tractable. According to this theory, the general solution of Eqs. 7a and 7b can be expanded in a series of exponential decays,

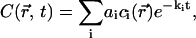(16)

where −k_i and 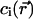are the eigenvalues and eigenfunctions of the time-independent differential equation associated to the diffusion-reaction Eqs. 7a and 7b. The coefficients a_i are chosen to satisfy the initial condition at time t = 0 (laser switching on), which is a uniform concentration,

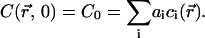(17)

Hereafter we are interested in giving an approximate solution to the Eqs. 7a and 7b, in the case of a top-hat laser profile of constant radius ω₀ (i.e., a parallel beam), in a cylindrical compartment. The problem therefore becomes rigorously a two-dimensional problem of revolution symmetry: an homogeneous circular bleaching zone of radius ω₀, centered in a circular compartment of radius R. Let us consider the eigenvalue equation obtained by inserting a solution of the form in the diffusion-reaction Eq. 7a,

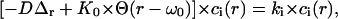(18a)

where is the photobleaching rate within the laser beam, Θ(r − ω₀) is the heavy-side function, and Δ_r if the radial part of the Laplacian in polar coordinates (due to the translational and rotational invariance, r is the only coordinate appearing in Eq. 18a). Note that the relation between K₀, the laser power P, the beam waist ω₀ and the photobleaching cross section σ_B differs by a factor 2 compared to that of a Gaussian beam (see above). Taking into account symmetry and boundary conditions

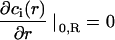(18b)

and continuity at the edge of the laser beam

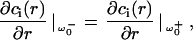(18c)

the solutions of Eqs. 18a–18c, can be expressed as linear combinations of Bessel functions, providing eigenvalues and eigenfunctions.

This approach is especially convenient to study the regime attained at long times. In this so-called quasi-stationary regime, all the terms of the expansion appearing in Eq. 16 vanish, except the slowest one, which corresponds to the lowest eigenvalue, k₁, of Eq. 18a. This means that, for times long enough, the concentration decreases everywhere with the same rate. This long time decay can be contrasted with the short time decay, t < τ_R, during which the bleaching hole is being formed. In other words, the short time decay corresponds to a superimposition of various eigenstates.

RESULTS OF SIMULATIONS

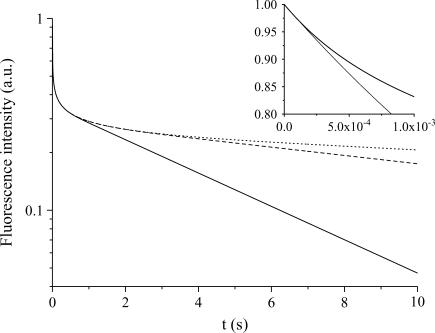
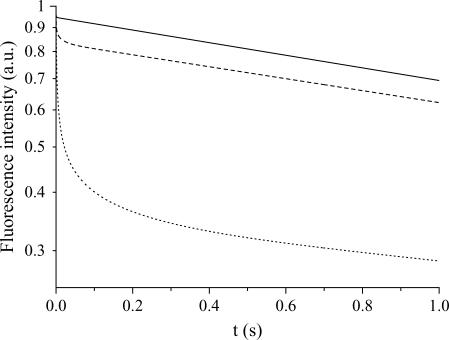
The evolution of the fluorescence signal is presented in Figs. 3–5 for various values of the control parameters that are the radius, R, of the compartment, the diffusion constant, D and the photobleaching rate at the laser beam waist, K₀. It was calculated by solving numerically Eqs. 7 and 8 according to the geometrical parameters defined in Model, and by determining the decay of the fluorescence intensity in the central region of the compartment. Whatever the values of these parameters, we can observe the same features in Figs. 3, 4, or 5: an exponential decline at very short times (barely visible since it occurs at a high frequency), which leads to the apparent discontinuity at the origin where the fluorescence intensity is normalized to 1. Then, after an intermediate temporal regime (the short time regime, see below), the signal decays in a quasi-exponential way at long times, providing a simple determination of the decay time by measuring the slope of the intensity signal in a semilogarithmic representation. In Model we conjectured Eq. 15, which states a simple relation between the size of the compartment and the fluorescence decay time attained at long times. One immediately sees in Fig. 3 that, in agreement with Eq. 15, the larger the compartment, the slower the long time decay. However, Eq. 15 does not give information about the intermediate regime occurring before the so-called quasi-stationary regime. It is therefore our goal to now discuss the different temporal regimes.

FIGURE 3.

Semilogarithmic representation of the fluorescence intensity (normalized to 1 at t = 0) as a function of time for various compartment radii: R = 10 μm (solid line), R = 20 μm (dashed line), and R = 30 μm (dotted line), with a given diffusion constant, D = 30 μm²/s and bleaching frequency, K₀ = 1 kHz. We observe the fast decay at short times controlled by the competition between the photobleaching and the diffusion. The inset shows the decay at very short times, which is independent of the compartment size. The thin line corresponds to the exponential fit in the neighborhood of t = 0.

FIGURE 4.

Fluorescence intensity as a function of time for several diffusion constants: D = 3000 μm²/s (solid line), D = 300 μm²/s (dashed line), and D = 30 μm²/s (dotted line), at a given bleaching frequency, K₀ = 1 kHz and compartment radius, R = 10 μm. We observe that the transition between the short time decay and the long time regime occurs at larger times when diffusion is slow.

FIGURE 5.

Fluorescence intensity as a function of time for two values of the photobleaching frequency: K₀ = 1 kHz (solid line) and K₀ = 3 kHz (dashed line), with a given compartment radius, R = 10 μm, and diffusion constant, D = 30 μm²/s. We can see that the crossover time between the short time decay and the long time behavior is only slightly affected by K₀.

Short, intermediate, and long time regimes

We observe in Fig. 3 that the very short time decay is independent of the compartment diameter, whereas the long time decay is dependent. From the length and timescales that appear in the problem we can expect three different regimes. In the initial stage (t = 0) diffusion does not play any role since the molecular concentration is homogeneous in the container. We can thus expect (and do observe in Fig. 3, inset) an exponential decay at very short times, before diffusion efficiently competes with bleaching. The typical time for diffusion to settle inside the beam waist is of the order of 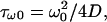which remains less than a millisecond for all molecules studied in this work. This very short time regime (t < τ_ω0) is thus hardly observable in practice and we shall consider the intermediate regime in the following. We shall denote the intermediate regime as the short-time regime. This short time regime corresponds to a competition between diffusion and bleaching, and leads to a nonexponential decay of fluorescence, as can be observed in Fig. 3, below a typical time of the order of τ_R = R²/4D, time for the diffusion profile to reach the edges of the compartment. The value τ_R is smaller than a few seconds for most of the situations encountered in this work. When t > τ_R, on the contrary, we enter in the long time exponential decay, also called the quasi-stationary regime.

To illustrate that the crossover time between the short and long time regimes depends essentially on the diffusion constant, Fig. 4 shows the fluorescence intensity for various diffusion constants at the same bleaching frequency. We do observe that indeed the crossover time decreases with D. The dependence of the crossover time with the bleaching frequency K₀ is tested in Fig. 5, and we can see that this dependence is very weak. The main effect of K₀ is to change the crossover intensity.

Long time regime versus beam profile and confinement

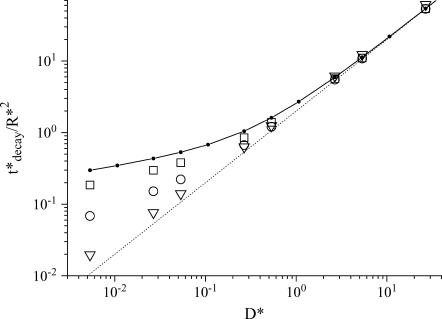
If we now consider the long time exponential regime, the decay time can easily be extracted from the fluorescence data and plotted on a single graph (Fig. 6) to check Eq. 15. Not surprisingly, the constant B is found to be exactly 2, while A is estimated to 0.4 for a focused Gaussian beam (see the +, ○, × symbols and the corresponding fit represented by a solid line).

FIGURE 6.

Variation of the decay time in the long time regime as a function of D* for a focused Gaussian laser beam and for various values of the control parameters R and K₀: 20 μm and 3 kHz (+); 10 μm and 3 kHz (○); and 10 μm, and 300 Hz (×). We can see that the master equation, Eq. 15, is nicely reproduced by fitting the numerical data, with A = 0.4 and B = 2 (solid line). The decay time corresponding to a parallel Gaussian laser beam with R = 10 μm and K₀ = 3 kHz (□) can also be fit with the master Eq. 15, but with A = 1.56 and B = 1.98 (dashed line).

Effect of the beam profile

We mention that the value of A is geometry-dependent. If instead of a focused Gaussian beam we consider a parallel Gaussian laser beam, its value varies in a significant way, although it remains of the order of unity (see the open square and the corresponding fit represented by a dashed line in Fig. 6).

Effect of the confinement

When the size of the compartment becomes of the order of the beam waist (ω₀ = 0.25 μm), the slow diffusion regime becomes progressively indistinguishable from the fast diffusion one (see Fig. 7). This is because all the molecules of the compartment are simultaneously irradiated, so that the diffusion does not play any role. In the extreme case where the size of the compartment is smaller than the beam waist, the decay rate reaches its maximum value, K₀, the bleaching frequency at the center of the cylinder. In this situation the fluorescence decay is exponential at any time.

FIGURE 7.

Confinement effects: we consider here a focused Gaussian beam and containers with radii R of 1 μm (square), 0.5 μm (circles), and 0.25 μm (triangles). For comparison, the solid line with dots corresponds to a large compartment (R = 10 μm) and the dotted line corresponds to the fast diffusion limit. In all cases, the laser power of the beam, P, is identical.

Long time regime in the two-dimensional approximation

One sees in Fig. 8 the agreement between the decay time of the exponential regime, deduced from the lowest eigenvalue, k₁, of the Sturm-Liouville Eq. 16, 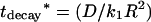and from the above-mentioned numerical calculations performed with a Gaussian parallel beam (see Fig. 6). The different definitions of K₀ (for the Gaussian and top hat profiles) do not prevent the comparison, since the relevant parameter, D*, used as an abscissa is a function of the laser power, P, and not of K₀. However, a small difference appears in the slow diffusion regime, where, as discussed above, the exact shape of the beam (Gaussian versus top-hat) does matter.

FIGURE 8.

Comparison between the lowest eigenvalue of the Eq. 18a (top-hat beam), circles, and the linear fit (t*_decay = 1.56 + 1.98D*) of the numerical calculations (parallel Gaussian beam), solid line.

EXPERIMENTAL RESULTS

Results in vesicles

Short time decays

As explained in Model, a very fast initial exponential fluorescence decay occurs on a timescale shorter than the diffusion time through the beam waist, 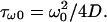For instance, the largest molecule used in this work (FITC-dextran FD250S) has a diffusion constant such that τ_ω0 ≅ 0.5 ms (assuming D = 19 μm²/s and ω₀ ≅ 0.2 μm). To correctly measure this very fast initial decay rate, one would need a very precise synchronization between the laser and fluorescence recording switching on. After this very short time regime, a nonexponential regime occurs, up to the time τ_R = R²/4D (see Model), time for the diffusion profile to reach the edges of the container. It is possible to put into evidence that, at the end of this intermediate regime, a photobleaching hole has been formed, the depth of which increases when the diffusion constant decreases and when the laser power increases. For that purpose, we compare the initial intensity of the vesicle confocal image recorded before starting the photobleaching process, I_image(0), with the value of the fluorescence count rate at the time τ_R = R²/4D after the beginning of the fluorescence decay, I_decay(τ_R). The intensities, I_image(0) and I_decay(τ_R), are normalized with respect to the laser power and to the pinhole aperture, to give a figure approximately proportional to the molecule concentration. Therefore, the ratio I_decay(τ_R)/I_image(0) indicates the loss of concentration that occurs during the short time decay. One sees in Fig. 9 that the smaller the diffusion constant or the larger the photobleaching cross section times the laser power, the more pronounced is the loss of fluorescence attained at the end of the short time regime. This figure has been drawn by concatenating the data corresponding to vesicles of various sizes, loaded with fluorescein-labeled molecules: FITC, FD4, FD70, and FD250S. The corresponding diffusion constants are those reported in Table 1, while the photobleaching cross sections are the ones determined from the time decays of fluorescein in vesicles (σ_B = 2.45 × 10⁻¹² μm², see below). The laser power ranges from 5.4 to 103 μW. We believe that the loss of fluorescence reported in Fig. 9 reflects the increase of the depth of the photobleaching hole when either the diffusion constant decreases or the photobleaching frequency rate, K₀, increases.

FIGURE 9.

Relative fluorescence loss during the photobleaching hole formation. The intensity of the image taken before continuously photobleaching, I_Image(0), is used to normalize, while the hole in fluorescence is evaluated, during the intensity decay, at the time of diffusion through the vesicle, I_decay(τ_R). The error bars correspond to the SD obtained by compiling the data of various vesicle sizes.

At this point it is interesting to note that the so-called bound fraction discussed in FRAP experiments would manifest, when applying our methodology to systems exhibiting bound species, in the amplitude of the fluorescence losses occurring at very short times. As a matter of fact these species do not contribute to the signal observed at long times (when diffusion and photobleaching compensate each other).

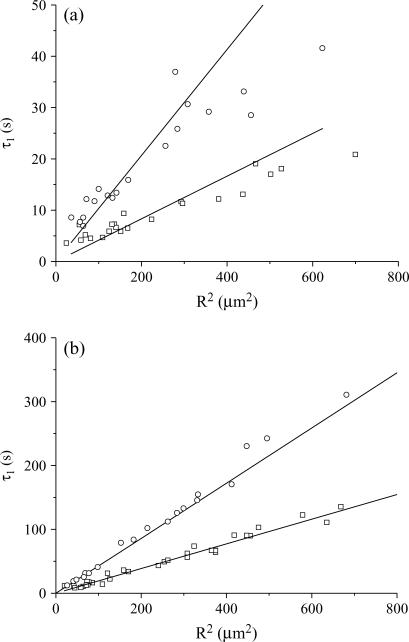
Exponential long time decays

We now focus on the long time decays by fitting the fluorescence rate decrease at times longer than τ_R. As explained in Materials and Methods, when bi-exponential fits are necessary, the longer of the two decay times is not retained and the shorter time τ₁ is assumed to be characteristic of the compartmentation, according to Eq. 2a. To compare our experimental results with the theoretical framework presented above, the following parameters have been varied: the photobleaching cross section (eGFP versus fluorescein- and FITC-labeled molecules); the diffusion constant of the molecules (see Table 1); the laser power P; the size of the compartment R. Whatever is the photobleaching regime (fast diffusion versus slow diffusion), one expects that the photobleaching time τ₁ scales with R², according to Eq. 2a. Indeed, this is what is observed, despite a pronounced dispersion around the expected behavior for FITC-dextran. Fig. 10 shows a comparison between eGFP and FITC-dextran FD70 and put into evidence, in addition to the dispersion of the results for FD70, the much larger photobleaching cross section of FD70. We tried to correlate the decay times that significantly deviate from the expected behavior with observable anomalies of the diffusion constant or of the vesicles (shape, internal structure). Since we were unsuccessful, we considered the whole ensemble of data without excluding any vesicles and attributed a unique diffusion constant to all the molecules of the same species, according to Table 1, whatever is the vesicle containing the molecules. Then, we obtained a mean value and an SD of the ratio τ₁D/R² for each ensemble of vesicles, loaded with the molecules of the same diffusion constant, D, and irradiated with the same laser power, P. Henceforth, these measured values could be fit with 0.4 + πD/σ_BP (see Eq. 2a) to give the photobleaching cross section, σ_B. We checked that fluorescein and FITC have the same photobleaching cross section, σ_B = (2.45 ± 0.39) × 10⁻¹² μm², while the photobleaching cross section of eGFP is found to be (0.066 ± 0.005) × 10⁻¹² μm². The FITC cross section is consistent with an estimation we previously made, which was between 3 × 10⁻¹² and 4 × 10⁻¹² μm² (19). It is possible to compare our σ_B value for FITC at 488 nm, with the one calculated, at the same wavelength, from the absorption cross section, σ_abs and the photobleaching quantum efficiency, φ_B: σ_B = σ_abs × φ_B. These parameters have been reported at pH 9: σ_abs = ɛ × 3.82 × 10⁻¹³ μm², where ɛ = 98 × 10³ cm⁻¹ M⁻¹ is the molar extinction coefficient (27) and φ_B = 0.8 × 10⁻⁴ (28). This leads to σ_B = 3 × 10⁻¹² μm², in very good agreement with our experimental results. In our earlier article (19), we did not properly calculate σ_B from (28), and found a less good agreement. The photobleaching cross section of eGFP can be compared with the value deduced from the parameters, 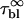and I_S, measured by Harms et al. (29) in bulk, that is σ_B = ( The complete ensemble of data (that corresponds to 354 vesicles) can therefore be plotted on a single synthetic graph (Fig. 11), which shows a very good agreement with the theoretical prediction.

FIGURE 10.

Variation of the characteristic decay time τ₁ in the long time regime versus the vesicle radius, R, for FD70 (a) at 13 μW (circles) and 43 μW (squares), and for eGFP (b) at 43 μW (circles) and 103 μW (squares). The straight lines are drawn to guide the eyes.

FIGURE 11.

Compilation of the photobleaching data (errors bars are SD) corresponding to all the studied molecules (fluorescein, FITC, streptavidin-fluorescein, FD4, FD70, FD250S, and eGFP), inserted into vesicles between 10 and 100 μm in diameter, under a laser power from 2.6 μW to 103 μW. eGFP data (squares) falls in the fast diffusion regime (5 < D/σ_BP < 200), whatever the laser power is, because the photobleaching cross section of eGFP is small. On the contrary, fluorescein- and FITC-labeled molecules (circles) have a larger photobleaching cross section and range from the slow diffusion regime to the fast one (0.04 < D/σ_BP < 10). The solid line corresponds to the theoretical Eq. 2a.

Results in cells

Knowing the photobleaching cross sections of FD4 and eGFP, our goal is now to analyze the decay times, measured on cells, with Eq. 2a and to calculate the size of the cellular structure that compartmentalize the fluorescent molecules. All the experiments on cells have been performed with the laser power set to P = 13 μW. It is worth to note that, for FD4, D* = 0.5 (D = 26 μm²/s, see Table 1), which corresponds to a situation of intermediate regime between slow and fast diffusion. On the contrary, the much weaker photobleaching cross section of eGFP (see above), is such that one is clearly in the fast diffusion limit: D* = 15 (D = 21 μm²/s, see Table 1).

Cells containing FITC-dextran FD4

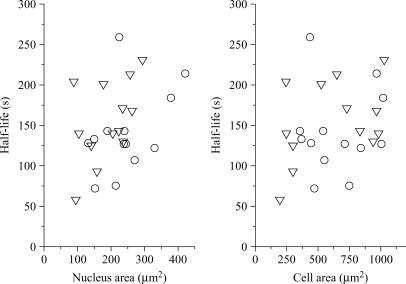
We have recorded the fluorescence decays of 23 cells, the nuclei of which were centered on the laser beam waist. As a first approach, we calculated the half-lives of the fluorescence decays, assuming the same baseline for all the cells, i.e., 8 kHz. We see in Fig. 12 that there is a clear correlation between the size of the nuclear and cellular compartments and the fluorescence half-life (the larger the compartment, the slowest the decay). However, since the sizes of the nucleus and of the cell are themselves correlated (data not shown), it is impossible to identify, from Fig. 12, which structure (nucleus or cell) compartmentalizes the fluorescent molecules. Therefore, to go further we have fit the fluorescence decays with bi-exponentials, providing two characteristic times, τ₁ and a longer one, τ₁′. Once again, the asymptotic base line, attributed to autofluorescence, was fixed to 8 kHz. From τ₁ and τ₁′ we calculated the corresponding radii R_τ1 and R_τ1′ according to Eq. 2a (with P = 13 μW, D = 26 μm²/s, and σ_B = 2.45 × 10⁻¹² μm²). Table 2 shows the statistical properties of the calculated radii, R_τ1 and R_τ1′, together with the measured radii of the nuclei and cells. We see in this table that the best correlation occurs between the measured size of the cell, R_cell, and that calculated from the shorter time component, R_τ1, although this calculated radius is, on average, slightly smaller than the measured one. In addition, we note that we could neither put into evidence a decay time characteristic of the nucleus, nor assign the longer time component τ₁′.

FIGURE 12.

Half-lives of the fluorescent decays of cells loaded with FD4, versus the measured sizes of the nuclei and of cells. The asymptotic base line is assumed to be 8 kHz. The nuclei are centered on the laser waist.

TABLE 2.

Radii for FD4 cells

	Mean value	SD	Minimum value	Maximum value
Rnucleus	8.50	0.82	6.84	9.91
Rcell	17.7	4.2	12.2	27.7
Rτ1	14.2	3.1	8.1	19.2
Rτ1′	30.1	5.5	17.5	43.0

Measured (R_nucleus, R_cell) and calculated (R_τ1, R_τ1′) values, in μm, of the characteristic radii of cells loaded with FITC-dextran FD4.

Cells containing eGFP

The situation is quite different for the 31 eGFP transfected cells that have been studied in two distinct experiments involving 18 and 13 cells. For these experiments the nuclei were also centered on the laser beam waist. First of all, the correlation between the size of the nucleus and cell and the fluorescence half-life is much less pronounced than for FD4 loaded cells, as can be seen in Fig. 13. This may be attributed to the fact that:

1. Two series of measurements have been compiled.

2. The cell density is higher for eGFP.

3. The transmission images are not as good as for FD4 cells.

Nevertheless, it is interesting to look for the compartment that, statistically, corresponds at best to the observed decay times. For that purpose, two characteristic times, τ₁ and τ₁′, are evaluated by fitting the experimental data with double exponentials (the base line is still fixed to 8 kHz). Using Eq. 2a (with P = 13 μW, D = 21 μm²/s, and σ_B = 0.066 × 10⁻¹² μm²), we have calculated the corresponding radii R_τ1 and R_τ1′, the statistical properties of which are reported in Table 3. In contrast with the previous case of FD4 loaded cells, the best agreement is obtained between R_τ1 and the measured nucleus radii, R_nucleus. However, here also is the calculated radius slightly smaller, on average, than the measured one.

FIGURE 13.

Same as Fig. 12, but with eGFP-transfected cells. The triangles and circles correspond to the two series of experiments.

TABLE 3.

Radii for eGFP cells

	Mean value	SD	Minimum value	Maximum value
Rnucleus	7.80	1.54	5.31	11.6
Rcell	13.2	3.42	7.89	21.4
Rτ1	5.62	1.73	2.98	9.75
Rτ1′	19.9	7.75	12.5	48.5

Measured (R_nucleus, R_cell) and calculated (R_τ1, R_τ1′) values, in μm, of the characteristic radii of eGFP transfected cells.

DISCUSSION AND CONCLUSION

We showed that the decay of fluorescence rate is, in a homogeneous and impermeable compartment, related to a limited number of parameters: the photobleaching cross section, σ_B, the laser power, P, the diffusion constant of the molecules, D, and the size of the compartment, R. When applying the central equation of this article (Eq. 2a) one can encounter several difficulties. First of all, the characteristic decay time τ₁ must be determined in the quasi-stationary regime, which is reached after the diffusion time through the compartment τ_R = R²/4D (see Materials and Methods). Hopefully, in most of the cases, a maximum of few seconds are necessary to reach this regime, while tens to hundreds of seconds can be available to evaluate the parameters of the quasi-stationary (or long-time) regime. Therefore, even if the short time decay is not completely excluded from the fit (because τ_R relies on parameters, D and R, that are not well known at the beginning of the analysis), its relative weight is weak and should not bias significantly the fit value of τ₁. Another difficulty comes from the fact that the cellular medium is neither homogeneous nor continuous.

Let us come back to the experiments with FD4 and eGFP cells. The ratio of the photobleaching cross sections of FITC and eGFP is ∼37. In our experimental conditions, the half-life of the fluorescence decays of FD4 in living cells is, on average, 10 s (see Fig. 12). If the compartmentation of the FITC-dextran and eGFP molecules was similar, one would expect, as a first approximation given by Eq. 2b, the mean half-life of the fluorescence decays of eGFP cells to be ∼370 s. In addition, we note that the measured diffusion constant of eGFP in cells (21 μm²/s) is slightly smaller than that of FD4 (26 μm²/s), which should still increase the mean half-life of eGFP fluorescence decays in cells above 370 s (see Eq. 2a). However, we see in Fig. 13 that the mean half-life of the eGFP fluorescence decays is, on average, 150 s. We suggest that the difference of permeability of the nuclear membrane to FD4 and eGFP explains the very different behaviors of FD4 and eGFP cells. Nuclear pore complexes are shown to be permeable to fluorescein-labeled dextran FD4 (30), but much less permeable to eGFP (31). For instance, the permeability of the nuclear membrane to eGFP estimated from FRAP experiments (31) is ∼0.011 μm/s, that is ∼50–100 times smaller than that for FD4 (30). This is not inconsistent with our experimental results on FD4 cells, which indicate that the characteristic size of the compartment is close to that of the cell (Table 2), while the characteristic size of the compartment for eGFP cells is close to that of the nucleus (Table 3).

To explore the role of permeability, we have performed simulations of photobleaching and diffusion within two compartments that are connected through an interface of permeability K (in practice, one inner cylinder of radius 7.5 μm, more or less permeable, located within an outer cylinder of radius 15 μm). Our preliminary calculations (data not shown) put into evidence bi-exponential long time decays. The shorter of these two times can be interpreted as a global photobleaching time within an effective compartment, the size of which is permeability-dependent: when the permeability increases from 0 to infinity, this time increases from the decay time within the inner compartment to that within the whole compartment (inner plus outer). The second time is rather related to the permeability of the interface: when it is very low, this times goes to infinity and when it is very high this time seems to merge with the shorter time.

It is interesting to give the reader some practical clue to evaluate the effect of the permeability. For that purpose, we suggest to compare two characteristic times: the first one, τ₁(R), is the global photobleaching time within the inner compartment of radius R, neglecting any permeability effect (τ₁(R) is thus calculated with Eq. 2a); the second one, τ_K, is the characteristic filling time of the inner compartment, due to the permeability, K, of its interface with an outer infinite compartment (neglecting any photobleaching effect). Following Wei et al. (31), τ_K = R/3K. Therefore, when τ_K ≪ τ₁(R), the observed photobleaching decay time is mainly dependent upon the size of the outer compartment (in our case, the whole cell), because the permeability does not retard the photobleaching process. On the contrary, when the permeability is not high enough, τ_K ≥ τ₁(R), the observed photobleaching decay time is mainly dependent upon the size of the inner compartment (in our case, the nucleus).

We applied this thinking to the case of eGFP, by assuming that K lies between 0.007 and 0.015 μm/s (31). This leads to τ_K between 357 and 167 s, respectively; in any case, longer than the calculated value of τ₁(R), that is, ∼80 s (R = 7.5 μm, the other useful parameters for Eq. 2a being those reported above for eGFP cells). This confirms our initial observation and interpretation, according to which the observed fluorescence decay is related to the size of the nucleus. The situation is different with FD4. As a matter of fact, by taking K between 0.5 and 1 μm/s (27), we found τ_K between 5 and 2.5 s, respectively, to be compared with τ₁(R) = 3 s (R = 7.5 μm, the other useful parameters are those reported above for FD4 cells). Our analysis of the experimental data indicates that the measured decay times are consistent with the size of the cell. This suggests that the permeability of the nuclear envelope to FD4 is greater or equal to 1 μm/s.

In an approach similar to that applied to diffusion and binding (18), we have developed a framework to analyze fluorescence decays in combination with FCS data. This allows us to get both local information about the mobility of the molecules (diffusion, thanks to FCS) and nonlocal information (compartmentation, thanks to photobleaching). The main goal of our methodology is to check if the measured fluorescence decay is consistent with the simple diffusion-reaction process within the close compartments observed in the images. If not, this means that something has been missed and thus necessitates to be taken into account: additional compartment, permeability, anomalous diffusion (see below), etc.

The next challenging step is certainly to join the three problematic issues (diffusion, compartmentation, and interactions with free or immobilized molecules) in a unified treatment of fluorescence data. Another interesting direction of work concerns the so-called anomalous diffusion, which has been discussed for many years (11). Note that this question is not independent of the previous issue of interactions and of compartmentation. As a matter of fact, to some extent, the anomalous diffusion can be attributed to interactions with macromolecular structures that may compartmentalize the molecules. One practical point at issue is that of the interpretation of FCS data in terms of anomalous diffusion versus two-component diffusion (32). Concerning this aspect, we stress the fact that our method is based on the properties of diffusion at both short distances (within the laser beam) and long ones (through the whole compartment). This track has already been explored by some authors (4,33), but our method is probably a simple and promising one to set up, to evaluate the anomaly of diffusion.