Malaria resurgence in the East African highlands: Temperature trends revisited

Abstract

The incidence of malaria in the East African highlands has increased since the end of the 1970s. The role of climate change in the exacerbation of the disease has been controversial, and the specific influence of rising temperature (warming) has been highly debated following a previous study reporting no evidence to support a trend in temperature. We revisit this result using the same temperature data, now updated to the present from 1950 to 2002 for four high-altitude sites in East Africa where malaria has become a serious public health problem. With both nonparametric and parametric statistical analyses, we find evidence for a significant warming trend at all sites. To assess the biological significance of this trend, we drive a dynamical model for the population dynamics of the mosquito vector with the temperature time series and the corresponding detrended versions. This approach suggests that the observed temperature changes would be significantly amplified by the mosquito population dynamics with a difference in the biological response at least 1 order of magnitude larger than that in the environmental variable. Our results emphasize the importance of considering not just the statistical significance of climate trends but also their biological implications with dynamical models.

The present and future impact of climate change in infectious disease dynamics is a pressing but controversial subject (1–7). Malaria is a major public health burden around the tropics (6, 8) with the potential to significantly increase in response to climate change due to the role of temperature and rainfall in the population dynamics of its mosquito vector (5, 9). Plasmodium falciparum and Plasmodium vivax are the most important malaria species for humans, and their range is limited at high altitudes by low temperatures (10); global warming could thus drive the geographical spread of the disease and produce an increase in incidence at higher-altitude sites. Both of these patterns were presented as likely outcomes of global warming by the Intergovernmental Panel on Climate Change (1). The question arises whether the increase of malaria incidence in the East African highlands since the end of the 1970s is already a manifestation of climate change. This has been extensively debated (5–7, 11–14).

One central piece of evidence against a role of climate has been presented by Hay et al. (11), who analyzed long-term meteorological records for four high-altitude locations in East Africa where malaria incidence has dramatically increased in the last two decades. They reported no significant trend for climatic variables, in particular temperature, and concluded that the number of months suitable for P. falciparum transmission has not changed in the last century. A response by Patz et al. (7) argued that the use of a global climate data set was inappropriate given its coarse resolution (0.5 × 0.5°) and the large altitudinal variation within these regions. Despite this caveat, it is relevant to ask whether there is evidence of warming in these records, and if so, whether the observed magnitude of change is of potential biological significance.

In this paper, we revisit the existence of trends for the four highland sites in the same monthly temperature records but now updated to incorporate the last 5 years to the present. A nonparametric analysis that decomposes the variability in the data into different components reveals that the dominant signal in three of the sites and the subdominant signal in the fourth one correspond to a warming trend. These components are all statistically significant, differing from those expected for red and white noise. We then address the question of whether the signal of warming by ≈0.5°C is biologically significant using temperature data to drive a model of mosquito population dynamics. Temperature is known to influence the mosquito life cycle and in particular the development rate of larvae and adult survival (e.g., refs. 15–17). The mosquito model (18) is driven here by both the original temperature time series and its detrended counterpart for each site. The relative difference (RD) in the output of the model for the two temperature regimes shows that the mosquito dynamics significantly amplify the temperature increase. Parametric models closer in formulation to the approach of Hay et al. (11) also demonstrate significant (linear) trends. We discuss the source of disagreement with their conclusions.

Data

The monthly temperature time series (Fig. 1) were extracted from the Climate Research Unit (CRU, Norwich, U.K.) global grid of 0.5° resolution (data set CRU TS 2.1) (19). The four grid points chosen for the analyses respectively contain the following locations of interest: Kericho in western Kenya (latitude, 0.30 S; longitude, 35.37 E), Kabale in southwestern Uganda (1.25 S, 29.71 E), Gikongoro in southern Rwanda (2.45 S, 29.85 E), and Muhanga in northern Burundi (3.02 S, 29.83 E). Reported malaria incidence shows significant increases at these sites in the last decades of the 20th century (ref. 11 and refs. therein).

Fig. 1.

CRU temperature time series at the four locations in the African highlands. The bold line shows the trend obtained for each of these data with SSA. Because the latitude of Muhanga is almost on the boundary between two grid points in the CRU global grid, both the grid points above and those below the latitude of 3.00 S were considered. All results remain the same for these two time series, and we report here only the results for the grid point centered at 2.75 S (a, Kericho; b, Kabale; c, Gikongoro; d, Muhanga).

Results

To examine the existence of a warming signal, we first applied a nonparametric method, Singular Spectrum Analysis (SSA www.atmos.ucla.edu/fcd/ssa), which decomposes the variability in the data into orthogonal components whose form is not specified a priori (refs. 20 and 21; Methods). This decomposition allows the separation of the significant signal from the noise in the data and the identification of (nonlinear) trends and periodic components including those with unharmonic shapes (22). The decomposition of the variability of all temperature time series with SSA shows that the dominant components contain both a nonlinear trend and a seasonal cycle. The seasonality is evident in the eigenspectrum as pairs of identical eigenvalues (22) (Fig. 2and Fig. 5, which is published as supporting information on the PNAS web site). The trend corresponds to the first eigenvalue in three of the sites, Gikongoro, Kabale, and Muhanga, and to the third eigenvalue, following the pair corresponding to seasonality, in Kericho (Fig. 2). In all cases, these dominant and subdominant components are significantly different from the null hypothesis considered and lie outside the limits of the 95% confidence interval defined by the values expected for a red noise process with similar decorrelation time τ = −1/log r, where r is the lag-one autocorrelation value. The null hypothesis of white noise was not considered, because it was inconsistent with the shape of the SSA spectrum (Fig. 2; see Methods). The reconstructed time series corresponding to the trend components is plotted in Fig. 1 for the four sites. It consists of a nonlinear trend, with an inflection point in the 1970s followed by an increase in the 1980s and 1990s of ≈0.5°C.

Fig. 2.

SSA. The plots show the different eigenvalues obtained by SSA for each of the four time series ranked by order of importance according to the variance they explain. The dominant eigenvalue in three of the four sites (c, Gikongoro; d, Muhanga; and b, Kabale) corresponds to the trend and is followed by a pair of eigenvalues associated with the seasonal cycle. In Kericho (a), this order is reversed, and the trend corresponds to the subdominant eigenvalue. The trend components account for 10%, 20.5%, 14.7%, and 18% of the total variance, respectively, for Kericho (a), Gikongoro (c), Muhanga (d), and Kabale (b). The respective reconstructed components are shown in Fig. 1 (those for the pair of subdominant eigenvalues in b–d and the dominant pair in a are plotted in Fig. 5). The bars specify the 95% confidence intervals generated with Monte Carlo simulations of red noise. Specifically, the error bars computed for each empirical orthogonal function represent 95% of the range of variance found in the state-space direction defined by that empirical orthogonal function in an ensemble of 999 red-noise realizations. Thus, the bars represent the interval between the 0.5% and 99.5% percentiles, and eigenvalues lying outside this range are significantly different (at the 5% level) from those generated by the red-noise process against which they are tested. The dominant eigenvalues for Gikongoro (c), Kabale (b), and Muhanga (d) and the subdominant eigenvalue for Kericho (a) lie outside this interval and are significantly different from noise. The application of SSA in combination with this red-noise test is known as “Monte Carlo SSA” (38). The ssa toolkit freeware software from www.atmos.ucla.edu/tcd/ssa was used for the analysis. A large order was selected to force a better separation of constituent components mainly at the lower frequencies (22) (a, Kericho; b, Kabale; c, Gikongoro; d, Muhanga).

With SSA, we detrended the temperature time series by reconstructing the data with all components other than the one corresponding to the trend. The mosquito model (see Methods) was then run for each site with both the original and the detrended temperature data. This stage-structured model is a simplified version of a discrete-time system originally built to simulate the dynamics of Southern House mosquitoes under varying temperature and rainfall regimes in Hawaii (18). The rainfall input, daily presence/absence of precipitation, was generated from the monthly CRU data on the total number of rainy days (see Methods) and was kept the same for both runs. The resulting temporal dynamics of mosquito adult abundance show differences between the runs. Fig. 3 shows the resulting differences in mosquito abundance for two sites, Kabale and Kericho. Results for Gikongoro and Muhanga (not shown) are similar in order of magnitude to those of Kericho. Although the temperature time series (original and detrended) exhibit a RD of no more than 3%, the same measure for mosquito abundance grows to 30–40% in Kericho (Fig. 3 a and c). In Kabale, for similar differences in the two temperature time series, the RD in the mosquito abundance is further amplified, with peak values well above 100%. The difference measure expresses a deviation between the original and detrended forcing relative to the mean detrended value over the whole period. This measure is akin to a coefficient of variation in the sense of evaluating a deviation relative to the magnitude of the mean. The difference in the biological response can be at least 1 order of magnitude larger than that in the environmental drivers. It is the largest in the site with the coldest average temperature. This result follows from the nonlinearity of temperature effects on mosquito parameters in the model. Specifically, the development probability G from larvae to adults is nonlinear with a threshold at low temperature values (below 15°C) that are too cold for development to proceed.

Fig. 3.

RD in mosquito abundances (a and b) and temperature (c and d) for two sites, Kericho (a and c) and Kabale (b and d). For mosquito abundances, the RD time series were computed for each of the 100 stochastic realizations of simulated rainfall (see Supporting Text, which is published as supporting information on the PNAS web site). The values shown here correspond to one representative simulation for each site. Gikongoro and Muhanga show patterns (not shown here) of similar magnitude to those for Kericho, because their mean temperatures are also similar. Kabale’s temperatures are colder and result in a much larger amplification of the temperature difference. In either case, the RDs between the original and detrended temperatures (c and d) are at least 1 order of magnitude smaller than the RDs they generate in the simulated mosquito abundances.

For one of the sites, Kericho, we can drive the mosquito simulations with observed daily rainfall values. The resulting change in relative abundance (RD) for the simulated mosquitoes is similar to those obtained with the simulated rainfall values based on CRU monthly data for the number of wet days (Fig. 6, which is published as supporting information on the PNAS web site).

Sensitivity analysis shows that the above amplification is not restricted to the mosquito parameters of these particular runs but applies to a large region of parameter space. Fig. 4 shows the mean and maximum amplification as a function of the developmental rate of the mosquitoes and the daily probability of immature survival. We focus on these two parameters, because they exhibited the strongest effects on RD in the random exploration of parameter space and the associated sensitivity test (see Methods). As expected, exact mosquito abundance is sensitive to variations in mosquito parameters, but the biological amplification of the temperature difference is a robust phenomenon (Fig. 4).

Fig. 4.

Sensitivity analysis for the mean (a and b) and maximum (c and d) of RD values in Kericho (a and c) and Kabale (b and d), as a function of larval survival and development rate in the mosquito population model. The filled circles correspond to the combination of parameters used in Fig. 3. Mosquito populations decay exponentially for parameter combinations lying in the white area at the bottom left of each graph.

The simulations further show a negative RD before 1980, when due to the nonlinear shape of the temperature trend, the detrended temperature time series has higher values than those of the original temperature. In other words, this temperature pattern indicates a period of lower temperatures than expected without the nonlinear trend. An interesting consequence of this pattern is that mosquito abundance in the model exhibits a larger jump between the end of the 1970s and beginning of the 1980s. This change is larger than would be expected under either a monotonically increasing trend or no difference in temperature before that time. The analysis reveals for all sites a similar timing of the transition from a negative to a positive difference in 1980, corresponding to the beginning of a warming signal.

Finally, to further test for the existence of a trend with an approach closer to that used previously in the literature (11), we also fitted linear parametric time series models [Seasonal Autoregressive Moving Average (SARMA) models, implemented in r, www.r-project.org] to the CRU temperature data from January to December 1950–2002. For purposes of comparison with previous results, we also considered the period of 1970–1995 analyzed in Hay et al. (11). Model selection indicated that the best parametric model (the one with the lowest Akaike Information Criterion) among the SARMA models specified in Eqs. 2 (see Methods) was either the one with an intercept and linear trend or the one with a linear trend only. The linear trend is statistically significant (different from zero) in all cases and for the two periods of time considered (Table 1 for 1950–2002; see Table 2, which is published as supporting information on the PNAS web site, for the results of 1970–1995). Additionally, none of the autoregressive (AR) or moving average components is a unit root (Table 1). We also tested simpler AR models with independent and identically distributed random noise but found that these models failed to remove the autocorrelation of the residuals.

Table 1.

Results of parametric (SARMA) time series model

Site	β̂	φ̂1	φ̂12	φ̂13	φ̂14	φ̂15	φ̂16	θ̂	σ̂2
Kericho	0.0099 ± 0.0002	0.625 ± 0.170	0.230 ± 0.080	0.186 ± 0.082	0.155 ± 0.083	0.211 ± 0.082	—	−0.236 ± 0.227	0.29
Kabale	0.0083 ± 0.0002	0.805 ± 0.115	0.132 ± 0.080	0.192 ± 0.080	0.185 ± 0.080	0.137 ± 0.083	—	−0.588 ± 0.158	0.28
Muhenga	0.0095 ± 0.0002	0.795 ± 0.121	0.189 ± 0.080	0.190 ± 0.082	0.174 ± 0.082	0.144 ± 0.084	0.124 ± 0.084	−0.573 ± 0.164	0.27
Ginkogoro	0.0098 ± 0.0002	0.824 ± 0.105	0.135 ± 0.080	0.161 ± 0.080	0.163 ± 0.081	0.115 ± 0.083	—	−0.619 ± 0.114	0.27

Parameter estimates and 95% confidence intervals for the SARMA model for each of the four sites in the period 1950–2002.

Discussion

The controversy surrounding the existence of climate trends in the 20th century in the African highlands is central to the current debates on the causes of the pronounced increases observed in malaria incidence in these regions over the last few decades. Our results on (CRU) temperature data at four high-altitude sites support the occurrence of a significant warming trend since the end of the 1970s of ≈0.5°C. This timing coincides with that of the increase in incidence reported in the literature (5). However, statistical significance alone does not address the biological relevance of such warming. A mosquito population model shows that the population dynamics of the vector can dramatically amplify even small changes in the climatic signal. Because observed mosquito densities in the highlands are so low (23), their abundance is an important variable for malaria transmission in these regions. By contrast, in endemic areas with generally high mosquito abundance, malaria incidence can exhibit a plateau and decline as a function of this variable with multiple possible explanations related to human behavior and parasite dilution (e.g., ref. 24).

Even though this is a simplified mosquito population model, it contains all of the relevant biology necessary to drive the dynamics: temperature dependence in development and mortality, density-dependence mortality in the larvae and a reasonable mechanism for rainfall-dependence mortality for larvae. Our estimates of RD for the mosquitoes are slightly conservative, because we did not include other population effects that might amplify the signal even further, such as a positive effect of temperature on fecundity (e.g., ref. 25). The only process that could depress mosquito population size at higher temperatures is increased desiccation of breeding cavities but, given the magnitude of the temperature signal increase (0.5°C over 20 years), we do not expect this process to have a major impact in vector population dynamics. Nevertheless, the interplay between temperature and rainfall could be explored in more detailed models, including the size distribution of breeding cavities. At a more phenomenological level, evidence has been reported with time series models for an effect of the interplay of temperature and rainfall on malaria in the African highlands, but this effect concerns the interannual cycles of the disease (9).

It is interesting to consider the pattern of warming described here and in particular the changes around 1980, in light of other climatic trends from the literature. Area averages of surface temperature over tropical land regions have trended upwards in the last 50 years (see figure 1 in ref. 26 for averages between 30°S and 30°N and figure 2.2 in Annex A of ref. 1). Analyses of observational data and the output of atmospheric general circulation models driven only by sea surface temperatures (SSTs) indicate that this warming pattern on land is driven by a similar trend in SSTs in tropical oceans (26, 27). Interestingly, SSTs in the tropical Indian Ocean exhibit an abrupt shift (≈0.3°C) to a warmer state around 1976 (refs. 28 and 29; see figure 2 in ref. 30 and refs. therein), concomitant with shifts in many different atmospheric circulation indices and the general trend of warming of (global) tropical oceans (26). At a more regional level on land, evidence has also been reported for increasing monthly minimum (nighttime) surface temperatures and decreasing diurnal temperature ranges over Eastern Africa (e.g., ref. 31). At this scale, however, significant geographical variation exists, with nighttime cooling often observed close to the coast and large bodies of water (e.g., ref. 31).

The beginning of the 1980s coincides also with the development of chloroquine resistance against P. falciparum in this part of Africa (5, 32). Unsuccessful treatment has been proposed as a major factor behind the observed changes in malaria in the past decades (5). Clearly, trends in climate and resistance need not be independent and could interact through changing selective pressures. Theoretical studies suggest that drug resistance would evolve fastest either under high transmission intensity when encoded by a single gene or at both low and high transmission intensity when two or more genes are involved (33). Similarly, demographic factors and land use change will also interact to modify the potential for malaria transmission (6, 12–14, 32, 34–36). The primary argument we make here is not that climate is the main driver behind higher malaria incidence, but that its role cannot be ruled out on the basis of lack of evidence for temperature warming in these regions. Ultimately, a better understanding of the respective roles of climate, drug resistance, and land-use change and the interplay of these concomitant underlying trends will require a more creative and complex set of mathematical models explicitly developed to examine their concomitant impact on malaria dynamics. Statistical analyses of time series patterns alone will not be sufficient to fully understand the subtleties of malaria transmission.

Our results differ from the previous findings of Hay et al. (11). The different conclusions do not arise from the nonparametric nature of our analysis. Parametric time series models confirm these findings. One possible source of discrepancy is the potential effect on model selection of first differencing the data, as in the Dickey-Fuller test applied by Hay et al. (11). Similarly, seasonality is treated differently in our models, with fewer terms (and therefore parameters) whose number is determined by model selection itself.

Because of its adaptive nature, SSA differs from the more classical decomposition of Fourier analysis and is in particular well suited to the analysis of nonstationary data, a property it shares with other more recent methods such as empirical mode decomposition (EMD) and wavelets (37). Given our focus here on trends and not on the localization of specific frequencies, we chose one of these flexible decompositions, although we expect EMD to provide similar results.

The caveats of using CRU data for time series analyses have been extensively discussed elsewhere (see ref. 7). The limitation of a coarse spatial resolution in a landscape of rapidly varying altitude has been especially underscored when no evidence for warming is found. However, the presence of trends in coarse resolution data must reflect their presence at a finer resolution at some locations unless there have been systematic changes in the number of stations over time. Systematic changes in station numbers can generate spurious trend patterns, for example by the removal of stations in locations with the coldest temperatures. We have extracted from the CRU data set the number of stations used for these four grid points over time, and there is no abrupt or monotonic change in these numbers across the end of the 1970s through to the 1980s. There is only a marked decrease in the number of stations at all sites since 1997. However, significant spatial variability could exist at finer spatial scales, and future work should examine these patterns. Spatial heterogeneity in temperature has been shown to be influenced by patterns of land use change with agricultural practices (35). The spatial scale of relevance to the vector itself and to the movement of the human population concerned must be determined to evaluate whether particular local stations, or even a single local station, are appropriate for addressing patterns of change in meteorological drivers.

Methods

SSA.

Based on principal component analysis, the method generates a set of eigenvalues and eigenvectors from a symmetric covariance matrix obtained by considering the data for a given number of lags (the “order” of the analysis). The eigenvalues quantify the variance associated with each eigenvector or empirical orthogonal function (EOF). Projection of the data onto a set of EOFs allows its reconstruction for selected components, such as those above the noise floor accounting for most of the significant signal. Reconstruction further allows detrending of the data by selectively removing the variability associated with the (nonlinear) trend. The Monte Carlo SSA test (MC-SSA, ref. 38) was used to distinguish signals from red noise, in its narrow sense. Both white and red noise can be considered. For white noise, the power spectrum (which decomposes the variance as a sum of sinusoidal waves of different frequencies) is flat with an equal representation of cyclic components of all frequencies. Thus, there is no significant temporal autocorrelation. By contrast, red noise, which is known to be more relevant to environmental data, is dominated by cycles of low frequency (long period) in its power spectrum and exhibits significant autocorrelations that decay over time (see, e.g., refs. 39 and 40). The SSA spectrum also shows distinct patterns for these two types of noise, and it is well known from geophysical studies that the typical decaying patterns obtained for temperature data are close to those generated by red noise but clearly inconsistent with white noise. For red noise, we specifically consider here a first-order autoregressive process, AR(1), given by x_t=φx_t−1+ε_t with 0< φ <1 and ε_t independent identically distributed normal errors. The test compares statistics of simulated red-noise time series with those of the climatic time series (20). A total of 999 randomizations were used for the computation of MC-SSA. MC-SSA estimates the parameters of the AR(1) model from the time series itself by using a maximum-likelihood criterion (38).

Mosquito Population Model.

Vector dynamics are described with a stage-structured model for the number of larvae (L) and adult Anopheles gambiae mosquitoes (M) written in matrix form as:

where P is the probability that a larva remains in the larval stage as a function of temperature τ, F is the average daily fertility of a female mosquito, G is the probability that a larva develops into an adult as a function of temperature, and S is the daily survival rate of an adult mosquito as a function of temperature (18). The transition probabilities P and G in this stage-structured model can be computed as derived by Crouse et al. (41):

where d(τ) is the number of days it takes for a mosquito egg to develop into an adult mosquito as a function of temperature, and S_L is the daily survivorship of larvae. Similarly, G can be computed as:

The number of days for larval development used to compute P and G was calculated as the inverse of the development rate. We modeled S_L as a function of larval density and rainfall S_L = sρ(R)D(L), where s is the “natural” survivorship of larvae (in the absence of limiting factors), ρ is a [0.1] bounded logistic function describing the survival probability of larvae as a function of the number of consecutive dry days R, and D is an exponential function that models the survivorship of larvae as a function of larval density. Both ρ and D are controlled by one parameter each (for more details on the functional forms, see ref. 18). Finally, the development rate of larvae and survivorship of adults as a function of temperature were calculated from functional forms reported elsewhere (42), in particular S(τ) = exp((4.4 − 1.3τ + 0.03τ²)⁻¹).

The model was run on a daily time step using CRU temperature and number of rainy days in a month. Daily temperature values were created from monthly temperature data by simple spline interpolation. The influence of rainfall is simulated by increasing larval mortality as a function of accumulated days with no rain to represent the combined effects of increased competition and desiccation of breeding sites. Because only the total number of rainy days is provided by the CRU records, we generated daily presence/absence data with a prescribed autocorrelation structure by using a Markov model with two states (rain and no rain) adapted from Caswell (43) and with the frequency of rainy days varying monthly as given by the CRU data. To specify a realistic autocorrelation structure, we used daily rainfall at a local station in Kenya (Hail Research Station, Kericho; latitude, 0.37 S; longitude, 35.27 E) (see Supporting Text and Fig. 7, which is published as supporting information on the PNAS web site, for details on rain simulations). For comparison, the model was also run for this site, Kericho, with both local and simulated rainfall. The transition matrix in the mosquito population model was updated daily according to the prevailing temperature and rainfall conditions.

A comprehensive sensitivity analysis of the mosquito model has been presented elsewhere (18). Here, we explore how changes in key model parameters affect the mean RD in mosquito abundance between original and detrended temperature time series. We chose four parameters: the natural daily survivorship of larvae s, the slope of the linear development rate of larvae as a function of temperature a, the intensity of density dependence d, and the sensitivity of larvae to drought ω. We did not include adult survival in this sensitivity analysis, because for the range of temperatures considered, the function S(τ) is fairly flat. Parameter ranges were established within biologically reasonable limits: s, 0.8–0.99; a, 0.0042–0.0069 (±25% of the experimental measured slope); d, 0.01–0.1; and ω, 0.01–0.1. Values for the four parameters were chosen at random within their range, and the model was run for both the original and detrended temperature time series from the 1980s until the present. At the end of the run (≈10,000 days), the mean was computed for the following measure of RD:

where M_i is the size of the mosquito population under the original temperature time series, and m_i is the size of the mosquito population under the detrended temperature time series, both at time i. The difference at each time is normalized by the average size of the mosquito population over the whole time period. This procedure was repeated 1,000 times for different random choices of parameter combinations. We then examined the effect of each of the parameters on the mean by fitting a linear regression model and determining the significant effects. Based on the results of this analysis, two parameters (the slope of larval development and larval survival) were selected for their higher influence on RD and examined systematically for their effect on this quantity.

SARMA Models (44).

The following three models were considered

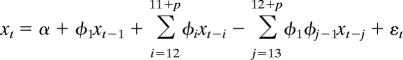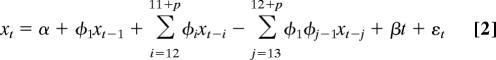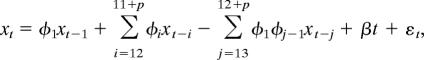where x_t is the temperature at time t, α is the intercept, φ₁x_t−1 represents a first-order AR(1) component, the sum terms represent the seasonal AR components [SAR(p)] for p ≥ 1, β corresponds to the linear trend in time, and ε_t represents the error. The error itself is given by a first-order moving average [MA(1)] process ε_t = θε_t−1 + ω_t, with ω_t independent identically distributed random noise of variance σ_wt², and initial condition

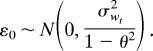The first and third models are nested within the second one. Model, error structure, and maximum number of seasonal lags, p, were chosen by using the Akaike Information Criterion. We do not consider here the model without the intercept and the trend, because the diagnostics resulting from its fit show that it is inappropriate for these data. In particular, the residuals were not independent, exhibiting significant autocorrelation.

Abbreviations

CRU

Climate Research Unit

SSA

Singular Spectrum Analysis

RD

relative difference

AR

autoregressive

SARMA

Seasonal Autoregressive Moving Average