Symmetry-, time-, and temperature-dependent strength of carbon nanotubes

Abstract

Although the strength of carbon nanotubes has been of great interest, their ideal value has remained elusive both experimentally and theoretically. Here, we present a comprehensive analysis of underlying atomic mechanisms and evaluate the yield strain for arbitrary nanotubes at realistic conditions. For this purpose, we combine detailed quantum mechanical computations of failure nucleation and transition-state barriers with the probabilistic approach of the rate theory. The numerical results are then summarized in a concise set of equations for the breaking strain. We reveal a competition between two alternative routes of brittle bond breaking and plastic relaxation, determine the domains of their dominance, and map the nanotube strength as a function of chiral symmetry, tensile test time, and temperature.

The highest strengths of solids are obtained from specimens of utmost uniformity and perfection. Even a single defect can cause drastic loss of strength. Thin solid filaments (whiskers) have long been viewed as material structures that can sustain the greatest mechanical tension (1, 2). Small cross sections permit little room for defects in their bulk, and the only heterogeneity is caused by inevitable presence of the surface and the interfacet edges. Discovery (3) of carbon nanotubes (CNTs) offered, at least in principle, the next level of perfection, when in a cylindrical network all atoms are equivalently tied to the neighbors, and no “weak spot” is apparent. This intrinsic uniformity, together with the known strength of carbon bonds, must lead to extreme resistance to mechanical tension, as has been anticipated all along (4, 5). On the other hand, establishing the quantitative level of breaking strain and identifying the details of atomic-scale rearrangements responsible for initial yield turned out to be elusive both experimentally and theoretically.

In recent years, much progress has been made in elucidating the atomic mechanisms of CNT failure. In experiment, refined loading techniques often based on atomic force microscopy and combined with electron microscopic imaging allowed one to measure the breaking-strain level and observe the overall failure patterns (6–10). The reported experimental values of breaking strain ranged within 2–19% because of variability of the samples and measurement conditions (6–8). In theory, bond rotation [that is a concerted movement of two atoms, known in chemistry as Stone-Wales isomerization (SW) (11)] has been recognized as a key step in mechanical relaxation (12–14). It leads to the lowest energy defect, a cluster of two pentagons and heptagons, 5/7/7/5. In the lattice of hexagons (the nanotube body) it represents a dislocation dipole, which explains its formation under high tension. This particular relaxation step is most favorable thermodynamically, but because of the high barrier of SW (15–17) it requires thermal activation. In contrast, another mechanism recently analyzed (18) needs no thermal activation but occurs at higher tension as a sequence of direct brittle bond-breaking steps, when a series of “lattice-trapped” states (19) can be identified. Further work has also begun (20, 21) in computing how the defects can reduce the CNT strength.

Despite these insights, the questions at what strain an ideal tube begins to yield and which primary atomic rearrangement is actually dominant remained unanswered. In this article, we present a simultaneous study of the two mechanisms, combining molecular dynamics (MD) simulations, careful quantum mechanical evaluation of the energy characteristics for the key configurations, and reaction rate theory (22) for the probability of yield event. This approach allows one to calculate breaking-strain values for nanotubes of different symmetry and diameter at different temperatures and load rates. Such a comprehensive view, inaccessible with direct MD, results in a strength map relating the load level, its duration, temperature, and chirality of the sample. The results of these calculations indicate that both ductile-type bond flip and the brittle bond-breaking mechanisms coexist and either can play the dominant role in failure in a particular test.

Results and Discussion

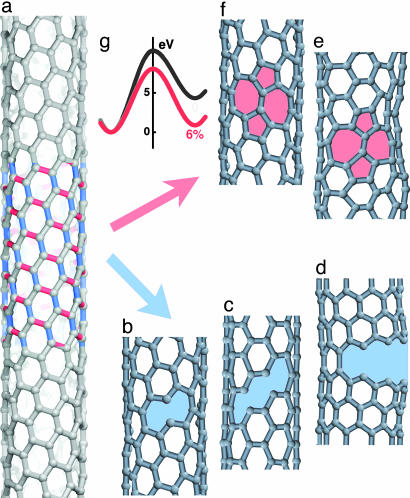
It is important to remember that even for a well defined flawless nanotube the tensile failure process depends considerably on a number of parameters, such as sample type (diameter d and chiral symmetry, i.e., the angle 0° ≤ χ ≤ 30° between the roll-up vector and the zigzag roll-up vector), applied strain ε, test duration t (or similarly, the strain rate dε/dt ≈ ε/t), and temperature T. Searching such a multidimensional parameter space in direct MD is impractical, even with the least taxing classical interatomic force field. However, MD remains a good tool for performing a preliminary hands-off search to identify the primary failure modes, which should then further be explored in detail. We have performed such simulations with quantum [nonorthogonal tight-binding approximation (23)] MD. We specifically considered different lattice temperatures and different applied tension (fixed degree of elongation). Different CNT types were considered with the test duration in subnanosecond range, well shorter than any experimental test. Fig. 1 illustrates, through selected representative configurations, the two main possibilities that emerge in the course of extensive simulations. Under high tension, the load is transferred differently to the bonds according to their orientations relative to the axis (color-coded in Fig. 1a). Further, the type of first lattice transformation depends qualitatively on temperature. At low T, thermal fluctuations appear insignificant and the yield event is purely “mechanical.” In this mode, one of the highly elongated bonds (marked blue in Fig. 1, for this “cold” mechanism) breaks and the crack-like configurations emerge (Fig. 1b). As discussed later, careful minimization with constraint (maintaining the tensile strain) shows (18) these states to be metastable, shallow energy minima, corresponding to the distinguishable n broken bonds (n = 1, 2, and 6 in the examples of Fig. 1 b–d), a nucleating brittle crack.

Fig. 1.

Alternative failure nucleation modes in CNTs. (a) A perfect tube under high strain (here ε = 15%) displays nearly longitudinal bonds (blue) more susceptible to direct breaking at low T, and those in circumferential direction (red) prone to thermally activated SW rotations. (b–d) Intermediate structures emerging in low-temperature simulations with different numbers of broken bonds n, in examples of a chiral tube at n = 1 (b), armchair type at n = 2 (c), and zigzag sample at n = 6 (d). (e) A 5/7/7/5 dislocation dipole emerges through SW isomerization at high T (note fluctuative lattice distortion). (f) SW defect relaxed at T = 0. (g) SW flip becomes thermodynamically favored at high tension but its formation still requires high activation, as computed energy profiles at ε = 0 and 6% illustrate.

In contrast, at high T, lattice fluctuations promote another bond movement (marked red in Fig. 1, for a “hot” mechanism). The bonds nearly transverse to the axial tension undergo a 90° rotation flip into almost longitudinal position (Fig. 1 e and f), thus lowering the energy. This SW rotation creates a dipole of dislocation cores 5/7, as in “plastic” yield (12–14). The formation of a SW defect becomes favorable under tension, but occurs rarely because of its high activation barrier (Fig. 1g).

It is important to further realize that the two primary yield mechanisms observed in MD, brittle crack or dislocation dipole, are in principle concurrent. However, the likelihood of their occurrence varies rather differently with the change of the sample or conditions. It resembles the brittle-ductile mode change in 3D solids, with silicon crystal as an example well explained from first principles (24). The goal of this article is to determine which of these mechanisms apply to the experimental conditions of tensile tests at ambient temperatures, a duration of seconds (instead of picoseconds as in generic MD run) and a CNT length >1 μm. Although some trends could be revealed in our early work (25) and especially in the detailed analysis of classical potential-based MD simulations (26), the force field used there tends to underestimate the activation barriers (15), while it is shown (27) to overestimate the forces at large strain, which essentially excludes possibility of brittle mode. Exploring full range of situations by extensive MD beyond classical force field is not realistic. Instead, we now evaluate each of the mechanisms by combined analytical and computational considerations, and then put the results together in a comprehensive map.

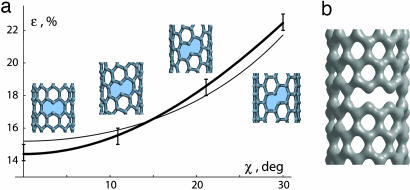
The key feature of the brittle path (sequential direct bond breaking) is that it does not require any thermal agitation. Tests can be performed on a series of CNTs, by applying elongation of different magnitude ε and then optimizing the structures of such prescribed length. In this way the failure strain ε_bb was determined for each tube, namely the upper strain level where the optimization converged (still stable) and the strain above which the tube fell apart. Computations show the diameter d (shell curvature) having small influence on ε_bb whereas the chiral symmetry role is significant. Fig. 2a plots the obtained breaking strain ε_bb (±0.4%) values versus the chiral angle, χ. The value of ε_bb systematically increases from the weakest zigzag type (χ = 0°, where the failing bonds are along the axis) to the strongest armchair type (failing bonds are at angle χ = 30° to the axis). Cauchy-Born rule of homogeneous deformation (1) helps to rationalize such dependence, by relating the gross elastic deformation ε with the individual bond elongation, δl/l = ½ ε [(1 − ν) + (1 + ν) cos 2χ], for the bonds most nearly along the tube axis (blue in Fig. 1a). Here ν ≡ S₁₂/S₁₁ = 0.16 is the Poisson ratio for graphite (1) and l is the equilibrium bond length. If the bond always fails at certain critical elongation (δl/l)_bb, this equation can be solved for ε, to estimate the brittle-breaking strain,

Computed breaking strains follow this dependence well (Fig. 2a, thin line), although the zigzag tubes fail a bit easier and the armchair type appears stronger than Eq. 1 predicts. This deviation can be caused by mutual influence of the adjacent bonds through charge transfer. In zigzag tubes, one bond is stretched distinctly higher than others, whereas in the armchair case, two adjacent bonds undergo identical strain. To formally account for this observed variation, one can add a small modulation into (δl/l)_bb = 1 − A cos 6χ, which yields excellent fit at A = 0.04 (Fig. 2a, thick line) with computer-experiment points. (Adding this correction reflects the fact that the lattice with a basis like graphene lacks inversion symmetry; thus it is not expected to follow Cauchy-Born rule precisely.)

Fig. 2.

Nonthermal failure. (a) Computed breaking strain dependence on chiral angle. At lower points the structures are still stable, whereas the upper strains lead to fracture. Inset configurations (much shorter than the full computed structures) show the breaking-bond orientations. The thin line corresponds to Eq. 1 and reasonably describes the trend, whereas a higher-order extrapolation yields a better fit (thick line). (b) In the vicinity of breaking strain, the lattice trapped states could be identified corresponding to the shallow minima at a different number of broken bonds, as seen in the computed electronic density distribution, here (10,0) tube, n = 2, metastable at ε = 14.5%.

Careful stability analysis for each of the brittle failure tests reveals the existence of intermediate metastable, lattice-trapped states. Each state corresponds to a distinct local minimum with n = 1, 2, 3, etc. bonds broken. Although absent without external tension, these states emerge near the failure point. Performed calculations of electron density distributions make the “missing” bonds apparent, as in the example of n = 2 in Fig. 2b. Important for further discussion, the barriers separating these crack nuclei are very small. A qualitative picture from calculations is that at the high load required to make a one-broken-bond state possible (as a metastable minimum) the barrier for its formation becomes insignificant [e.g., <20 meV for a (10,0) tube (18)]. For this reason, the brittle bond-breaking strains ε_bb are not sensitive to T or t, and as soon as the threshold is surpassed, the sample fails.

An entirely different pattern, also observed in MD simulations, is the dislocation dipole 5/7/7/5. Thermodynamically favorable at relatively low strain [ε = 5–9% depending on tube type (13, 14, 28)], these defects remain kinetically inaccessible because of the large activation barrier, E*. The lattice relaxation can take this route either at an exceedingly long time t or if the elevated temperature facilitates SW bond flip (Fig. 3a). Its probability rate is Nνe^−E*/kT, where ν = kT/h ≈ 10¹³ s⁻¹ is the standard expression from transition-state theory (22) for the frequency of attempts to cross the transition state (if one neglects the vibrational entropy change S* upon activation). Here N is the number of equivalent bonds in the sample, which is typically one-third of all of the bonds. Therefore, SW probability over the test duration t becomes high (≈1) if the barrier is sufficiently reduced by the applied tension to the “demarcation energy” level

It may even occur before brittle failure, at lower strain. What conditions make each of these mechanisms dominate and thus determine the observable strength of the ideal tube? To answer this central question, the energy landscape for the SW rotation should be explored, especially how the activation barrier E*(ε, χ, d) varies with the tension (ε) and among the tubes (χ, d).

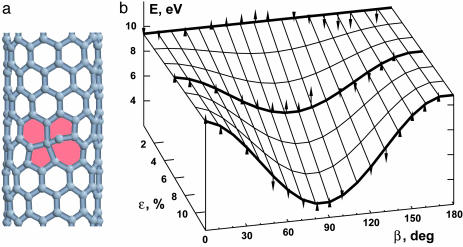
Fig. 3.

Transition state and barriers for SW transformations. (a) Saddle point geometry computed for a counterclockwise bond rotation in a (10,0) tube (the bond is also tilted off plane). (b) Barriers for a number of tubes at different tension (ε = 0, 6%, and 12%) as a function of the angle β between the bond (in its initial position) and the tube axis. Small arrows indicate whether the exact computed barrier is above or below the analytical approximation of Eq. 3, plotted as a surface.

To find this functional form, we combined simple symmetry arguments with the extensive numerical computations for a number of bond rotations in different tubes. First, computed E* values show little dependence on the curvature 1/d, which will be omitted below. Second, changing the strain sign (ε → −ε) affects the barrier height, and therefore there is a nonvanishing linear term. Third, tension inversion leads to an indistinguishable configuration, and thus there must be a 180° period in the angular dependence (i.e., 2χ is the lowest harmonics). Further, to quantify the activation barrier dependence, a number of saddle-point search computations were performed for the nearly equal diameter tubes (10,0), (8,2), (7,4), and (6,6) of chirality χ = 0°, 10.9°, 21.1°, and 30° respectively. For every tube we considered three generic bonds with two flip directions for each bond. It is convenient to refer to a particular bond by its angle β relative to the tube axis (note that χ = min β, among the three bonds, that is 0° and 30° for the zigzag and armchair types). Fig. 3b plots E* for all computed transition states and shows a great deal of regularity. The strain-free E* depends very little on β. However, under applied tension, the barriers linearly increase or decrease, depending on the bond-to-axis angle β, and at a larger strain a pronounced sinusoid develops. All computed barriers can be captured in one analytical form,

plotted as a surface in Fig. 3b, in overall agreement with the large set of computed points. The clockwise SW rotation of a bond initially closest to the circumferential direction, β ∈ [60°, 90°], has the lowest barrier, which still remains significant up to large strains.

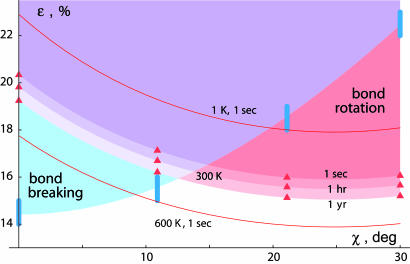
We are now in position to calculate strain for the SW yield, compare it with the brittle threshold of Fig. 2, determine the dominant yield mechanism, and map the strength for different tube types and conditions. For a 1-μm long tube (≈10⁵ atoms, i.e., N ≈ 5 × 10⁴) of given chirality χ (and therefore given angle β), at T = 300 K, one can substitute Eq. 3 into Eq. 2 and solve it to find the strain ε_SW(χ) where dislocation yield becomes probable within a given test time (15). The resulting family of curves (t = 1 s, 1 h, 1 yr in Fig. 4) determines the domain where this hot mechanism is likely to occur. Concurrently, the cold brittle failure comes about, and its critical strain is also plotted. Both mechanisms of failure nucleation display strong dependence on the nanotube symmetry (χ), with the zigzag type being more at risk to brittle failure (18), whereas the plastic yield is more easily induced in the nearly armchair type [note that thermodynamically most favorable SW rotation is in the armchair type (12, 13, 28)]. The effect of temperature is significant for the SW mechanism (as the curves for T = 600 K and 1 K illustrate), but is negligible for the brittle, almost barrierless (18) failure. Test time (or strain rate) naturally determines the cumulative probability of SW yield, and the critical strain for SW yielding lowers with the test duration as shown. Sample size enters Eq. 2 in the same way as time, and its influence is similarly mitigated by the logarithm, causing only insignificant strength reduction for a 10-fold or even 100-fold larger sample [Note that Weibull distribution (1) used commonly for the imperfect macroscopic fibers is based on statistics of flaws and does not apply to nearly ideal crystals considered here.] As the first SW flip occurs at the yield strain, it introduces imperfection that serves as a stress concentrator, generally weakening the CNT, and leading to further failure. If the bonds in the defect vicinity were more resistant to load, then a recurrence of SW all over the lattice would form a pattern similar to pentaheptite (29), an interesting, although unlikely, structural transformation beyond the scope of this study. In contrast to the SW mechanism, brittle failure occurs almost instantaneously when the threshold is reached, with time and temperature playing little roles.

Fig. 4.

Breaking-strain map for nanotubes of different symmetry (χ) at various load durations (t) and thermal conditions (T). The yield mechanism is determined by what borderline is crossed first as the tension is applied from ε = 0 upward. Brittle-bond breaking is marked by the failure intervals (dark blue segments) for specific tube samples and by extrapolated dependence on the chiral angle χ (blue-domain border); it has no perceptible dependence on T or t. Plastic yield through thermally activated bond rotation depends on temperature and test duration, as shown by the strain required to form a defect within the given test time (t = 1 s, 1 h, 1 yr); it was computed for specific tubes (red triangles) and extrapolated to arbitrary tube symmetry (red-level rims) by using Eqs. 2 and 3. Additional thin red lines show the yield strain at very low (T = 1 K) and higher (T = 600 K) for t = 1 s. At very high T (>2,000 K), the yield is no longer limited by activation but is rather controlled by the thermodynamic benefit of SW defects, achieved at ε ≈ 5 [sin (2χ + 30°)]⁻¹% (13).

The general chirality dependence looks in an interesting way complementary for the alternative plastic and brittle mechanisms (with the former dominating for armchair and the latter for zigzag symmetry), and their crossover shifts left or right depending on specific test conditions. Although the exact values of breaking strains could be further refined through more precise quantum-mechanical computations, the map of Fig. 4 summarizes the interdependencies of strain, symmetry, time, and temperature. Note that electron beam radiation, often used for visualization of failure, can facilitate SW flips similarly to very high T, giving the impression of a plastic behavior (9, 10). Plasticity can also be purposefully achieved by electrical current in a strained CNT (30). Inversely, the diameter and chirality change caused by the plastic relaxation can modify electronic properties of the CNT (13, 31). Although the main focus of the present study was ideal, flawless nanotubes, their utility (notably structural applications in the composite materials) requires the addition of functional groups, a derivatization. This chemistry partially disrupts the carbon bond network and should facilitate yield to high tension, thus reducing the intrinsic strength. Details of derivatization effects on the strength value or even change of the dominant mechanism (in the map of Fig. 4) can be explored with an analogous approach but remain beyond the scope of this article. Finally, the presented approach can be applied to other nanotubes, notably boron-nitride (17, 32) and even metal disulphides (33), where an ideal cylindrical lattice can respond to great tension in similar ways.

Methods

In our finite temperature MD simulations, for the force model we used the nonorthogonal, density functional theory (DFT)–based, tight-binding approximation (TBA) (23, 34), with periodic boundary conditions. The tensile strain was typically applied in small increments and the temperature increase was performed in conjunction with the Nose-Hoover thermostat (35). The DFT TBA has proven to be accurate for carbon systems (36), yet it permits sufficiently long MD simulations on systems large enough (≈200 atoms) to detect primary yield events at different conditions (T, ε, t) but within the same model. With a time step of 0.2 fs, the longest runs were 0.1 ns at high temperatures T = 2,000–3,000 K, in search for SW, e.g., in Fig. 1e.

In calculating the energy landscape associated with these processes, for quantitative accuracy we used the semiempirical AM1 (37) method and ab initio DFT with the functional of Perdew, Burke, and Ernzerhof (38) and the double zeta quality 3–21G basis set. Superior to tight-binding approximation, these methods account for the electronic charge density in a self-consistent fashion, thus being effective in providing for the charge transfer. Computations were performed with the Gaussian package (39) where both methods were implemented. Finite tube segments were terminated with hydrogen atoms at the edges.

To obtain the location of saddle points for the SW flips, the synchronous transit-guided quasi-Newton method (40) was used. To impose the external strain, the geometries were optimized under the constraint of fixed distances between pairs of atoms located at opposite ends. This method, applied with both AM1 and DFT, revealed only one transition-state type with a single atom buckled out of the CNT wall [not three possibilities found earlier with a classical force field in the case of a symmetric flat graphene sheet (15)].

All numerical values presented in Figs. 2 and 3, and therefore the curves in Fig. 4, were obtained with AM1. Overall, the accuracy of less expensive AM1 was satisfactory. Computed geometries of interest (SW defects, transition states, lattice trapped cracks) are practically indistinguishable when obtained with AM1 or DFT (in fact, the structures in Figs. 1 d and f and 3a are obtained with DFT computations). Several points verified with DFT show a general increase in SW barriers by <0.4 eV and in the yield strains by <1%, while showing no change in the dependencies.

Abbreviations

CNT

carbon nanotube

SW

Stone-Wales isomerization

MD

molecular dynamics

DFT

density functional theory.

Note Added in Proof.

Recent observations of ductile deformations of bending (30), necking and coalescence (41), and extensive elongation (42) generally support the possibility of plastic yield at elevated temperatures, as discussed above. Although the focus of present analysis was intentionally restricted to the primary yield, the reported experiments show rather rich in situ behaviors beyond the yield point. Remarkable evidence (42) of large plastic stretching at the temperatures near sublimation display distinct features in agreement with early theoretical predictions (12-14, 31): kink nucleation, their spiral movement, and stepwise (quantized) change of diameter in the course of elongation. It has not escaped our notice that other compelling details (42), such as significant loss of mass and longitudinal kink propagation, call for additional theoretical consideration (F. Ding, K. Jiao, M. Wu, and B.I.Y., unpublished work), including high-temperature mechanisms of pseudo-climb and diffusion.