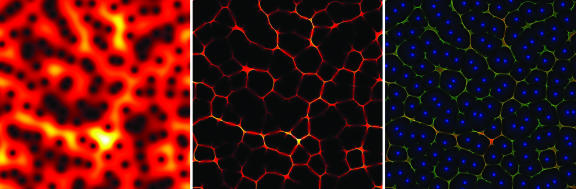
Fig. 2.

Analysis of a discrete white-noise signal, consisting of N independent identically distributed Gaussian random variables. (Left) |χ|, represented by false colors; red and yellow show high values, and black shows zero. The horizontal axis is time and the vertical axis is frequency, as in a musical score. Although the spectrogram of white noise has a constant expectation value, its value on a specific realization fluctuates as shown here. Note the black dots pockmarking the figure; the zeros of χ determine the local structure of the reassignment transformation. (Center) The reassigned spectrogram concentrates in a thin, froth-like structure and is zero (black) elsewhere. (Right) A composite picture showing reassigned distributions and their relationship to the zeros of the STFT; the green channel of the picture shows the reassigned Lebesgue measure, the red channel displays the reassigned sonogram, and the blue channel shows the zeros of the original STFT. Note that both distributions have similar footprints (resulting in yellow lines), with the reassigned histogram tracking the high-intensity regions of the sonogram and form a froth- or Voronoi-like pattern surrounding the zeros of the STFT.