Abstract
No proper statistical test is available for the evaluation of deviation of a single homozygous genotype from Hardy-Weinberg equilibrium (HWE) proportion. We propose a 1-d.f. χ2-test. The power of the proposed test is favorable compared to existing HWE testing procedures. The applications of this test are discussed.
STATISTICAL tests for the overall deviation from Hardy-Weinberg equilibrium (HWE) proportions have been well studied and widely used. These include the traditional χ2-goodness-of-fit (GOF) tests (Li 1955; Elston and Forthofer 1977; Emigh 1980; Smith 1986) and those using the exact approach (Louis and Dempster 1987; Guo and Thompson 1992).
In addition to checking for overall fit to HWE proportions, researchers are interested in learning whether one or several specific genotypes are over- or underrepresented. For example, researchers may suspect a bias in detecting particular genotypes or that selection may be acting to increase or reduce the frequency of a particular genotype. For the deviation of a single heterozygous genotype, Hernández and Weir (1989) suggested a 1-d.f. χ2-test and Chen and Thomson (1999) derived the correct variance of this individual heterozygous genotype test statistic under the null hypothesis. For the evaluation of a single homozygous genotype, however, little work has been done and researchers have been using an unreliable ad hoc 1-d.f. “GOF” test (e.g., Sebetan and Hajar 1997). In this note, we propose an appropriate 1-d.f. χ2-test for this purpose and discuss its properties.
Notation:
Given a random sample of n subjects from a diploid population, let the number of unique alleles be m, with sample allele frequencies pi, i = 1, 2, … , m, and the corresponding population allele frequencies Pi, i = 1, 2, … , m.
Let Xik be the number of subjects with genotype (Aik) in the sample, with sample genotype frequencies pik = Xik/n, i, k = 1, 2, … , m and the corresponding population genotype frequencies Pik. The random vector X = {Xik, i, k = 1, 2, … , m} then follows a multinomial distribution with probability vector P = {Pik, i, k = 1, 2, … m}, and ∑i,kXik = n.
Using notation similar to that of Hernández and Weir (1989), the population Hardy-Weinberg deviation coefficient for a heterozygote, Aik (k ≠ i), is defined as Dik = PiPk − (1/2)Pik, with the corresponding sample deviation coefficient dik = pipk − (1/2)pik. Similarly we define the population deviation coefficient for a homozygote, Aii, as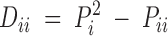 
, with the corresponding sample deviation coefficient 
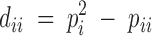. The Dii parameters are bounded by the following condition: −Pi1 − Pi ≤ Dii ≤ P2i.
The derivation of the test statistic:
Given the constraint that pi = pii + (1/2)∑k≠ipik, we have
 |
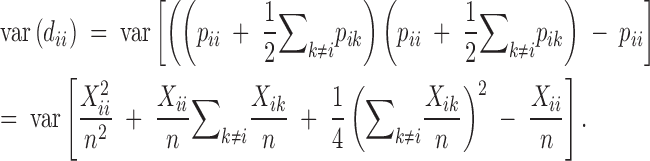Applying Fisher's formula for the variance of a function, T, of multinomial variates, X (Bailey 1961), we have varT ≈ ∑i,k∂T/∂Xik2o · npik − n · ∂T/∂n2o, where the subscript “o” indicates expectation. Therefore,
 |
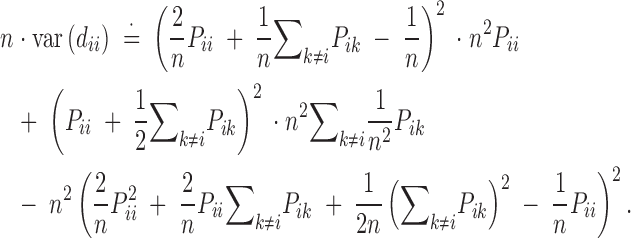Under the H0: Dii = 0, and given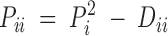 
and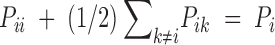 
, we have
 |
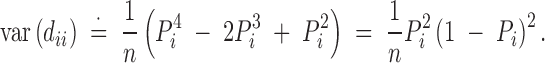The χ2-test statistic can then be calculated using sample allele and genotype frequencies as
 |
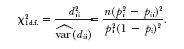This single homozygous genotype test can be easily implemented. A program for this test written in Splus is available upon request from the corresponding author (J.J.C.).
Statistical power of the test:
We compared the statistical power of the single homozygous genotype test with that of three other Hardy-Weinberg testing procedures: the overall χ2-test, the Markov chain Monte Carlo (MCMC) exact test of Guo and Thompson (1992), and the ad hoc 1-d.f. χ2-GOF test. We simulated data for three, four, five, and eight alleles. In each case, we used two different allele frequency distributions, one even and one skewed. For the skewed distribution, we considered two situations: when the allele associated with the specific homozygote of interest (A11) has the highest and the lowest allele frequency.
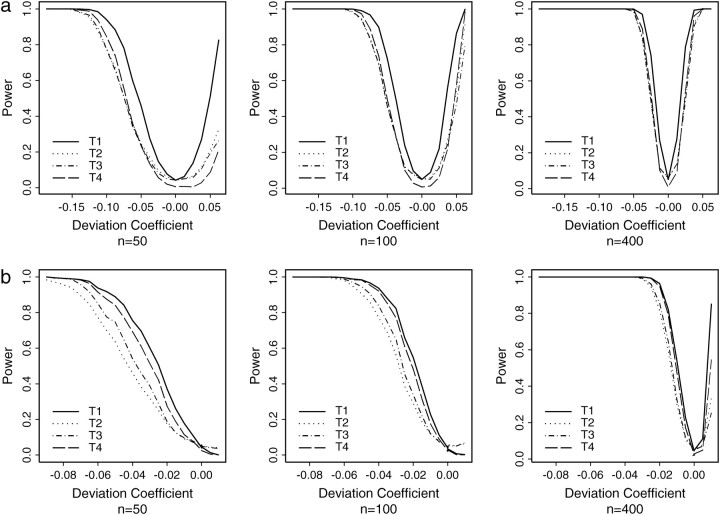
For each scenario, we considered 20 different levels of the deviation coefficient (D11) for the specific homozygotes of interest (A11), ranging from the minimum to the maximum possible values of D11. Given D11, the deviation coefficients of other genotypes, Aik (k ≠ 1, i ≠ 1), of the population were assigned proportionally to the minimum or maximum possible values of the Dik (k ≠ 1, i ≠ 1), constrained by the allele and genotype frequencies. We simulated 1000 samples from each “population” with the specified allele frequency distribution and deviation coefficients. Type I error rates, at D11 = 0, for the four procedures are summarized in Table 1. The power graphs for both an even and a skewed allele frequency distribution with four alleles are presented in Figure 1.
TABLE 1 .
Comparison of type I error rates among four Hardy-Weinberg testing procedures (α = 0.05)
| Sample size |
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 50 |
100 |
200 |
400 |
||||||||||||||
| Setting | Type I error rate (%) | T1 | T2 | T3 | T4 | T1 | T2 | T3 | T4 | T1 | T2 | T3 | T4 | T1 | T2 | T3 | T4 |
| Three alleles | |||||||||||||||||
| Even | (1/3,a1/3, 1/3) | 4.5 | 5.2 | 4.8 | 0.7 | 4.9 | 5.3 | 5.0 | 0.3 | 5.5 | 5.6 | 5.7 | 0.3 | 6.2 | 5.5 | 5.2 | 0.2 |
| Skewed | (0.5,a 0.3, 0.2) | 6.3 | 5.1 | 4.5 | 0.0 | 4.7 | 3.6 | 3.6 | 0.0 | 5.7 | 5.6 | 5.3 | 0.0 | 3.8 | 4.7 | 5.0 | 0.0 |
| (0.2,a 0.3, 0.5) | 4.0 | 6.5 | 5.8 | 1.4 | 3.8 | 4.7 | 4.0 | 0.7 | 4.8 | 4.0 | 3.9 | 1.6 | 5.0 | 4.8 | 4.8 | 1.1 | |
| Four alleles | |||||||||||||||||
| Even | (1/4,a1/4, 1/4, 1/4) | 4.2 | 4.4 | 4.2 | 0.5 | 4.9 | 5.2 | 4.7 | 0.6 | 5.2 | 4.7 | 4.8 | 0.7 | 4.9 | 5.9 | 6.0 | 0.9 |
| Skewed | (0.4,a 0.3, 0.2, 0.1) | 5.0 | 4.3 | 4.2 | 0.1 | 4.8 | 5.4 | 5.4 | 0.3 | 6.1 | 6.1 | 6.1 | 0.1 | 4.2 | 4.4 | 4.5 | 0.2 |
| (0.1a, 0.2, 0.3, 0.4) | 4.6 | 4.9 | 4.8 | 2.5 | 3.4 | 5.8 | 5.1 | 2.8 | 2.3 | 5.1 | 5.1 | 1.5 | 4.8 | 5.2 | 4.9 | 2.7 | |
| Five alleles | |||||||||||||||||
| Even | (1/5,a1/5, 1/5, 1/5, 1/5) | 3.7 | 5.3 | 4.3 | 1.1 | 3.7 | 4.2 | 3.9 | 0.7 | 4.6 | 4.2 | 4.2 | 1.2 | 4.3 | 4.0 | 3.6 | 1.5 |
| Skewed | (0.3,a 0.25, 0.2, 0.15, 0.1) | 4.6 | 4.6 | 4.3 | 0.5 | 5.4 | 5.0 | 4.3 | 0.5 | 5.4 | 5.1 | 4.9 | 0.7 | 5.2 | 5.0 | 4.8 | 0.4 |
| (0.1,a 0.15, 0.2, 0.25, 0.3) | 5.4 | 5.5 | 4.2 | 2.8 | 3.0 | 4.7 | 4.6 | 1.6 | 2.7 | 4.6 | 4.4 | 1.7 | 4.6 | 6.4 | 6.2 | 2.8 | |
| Eight alleles | |||||||||||||||||
| Even | (1/8,a1/8, 1/8, 1/8, 1/8, 1/8, 1/8, 1/8) | 4.8 | 5.1 | 4.6 | 3.4 | 3.6 | 5.1 | 4.3 | 1.9 | 4.7 | 4.3 | 4.6 | 1.6 | 4.5 | 5.9 | 5.7 | 3.2 |
| Skewed | (0.16,a 0.15, 0.14, 0.13, 0.12, 0.11, 0.10, 0.09) |
3.9 | 4.2 | 3.9 | 1.7 | 4.9 | 5.2 | 4.4 | 1.2 | 4.0 | 5.4 | 5.3 | 2.1 | 4.2 | 5.9 | 6.0 | 1.8 |
| (0.09,a 0.10, 0.11, 0.12, 0.13, 0.14, 0.15, 0.16) |
5.1 | 5.5 | 3.6 | 2.2 | 4.0 | 4.4 | 4.2 | 2.9 | 2.7 | 6.1 | 5.0 | 1.9 | 3.6 | 5.6 | 4.9 | 2.2 | |
T1, single homozygous genotype test; T2, Guo-Thompson exact test; T3, overall χ2-test; T4, 1-d.f. “GOF” test.
Homozygote of this allele studied.
Figure 1.—
Power comparison among the four Hardy-Weinberg testing procedures for simulated data: (a) four alleles and an even allele frequency distribution of (1/4, 1/4, 1/4, 1/4), testing the homozyote of a particular allele; (b) four alleles and a skewed allele frequency distribution of (0.4, 0.3, 0.2, 0.1), testing the lowest-frequency allele (T1, single homozygous genotype test; T2, Guo-Thompson exact test; T3, overall χ2-test; T4, 1-d.f. “GOF” test).
The single homozygous genotype test, together with the overall χ2-test and MCMC exact test (Guo-Thompson test), show reasonable type I error rates. The ad hoc 1-d.f. GOF test tends to be conservative, with very low type I error rates.
The statistical power of the single homozygous genotype test to detect homozygous genotype deviations from HWE proportions is superior to the three other tests, across all the test settings studied. Although the range of possible values for the deviation coefficient varies, the overall pattern of the power curves is not affected by the number of alleles or whether the overall allele frequency distribution is even or skewed. Instead, they are directly related to the allele frequency of the homozygote tested and the sample size.
When the frequency of the allele of interest is relatively high, the statistical power is relatively balanced in terms of detecting either homozygote deficiency (D11 > 0) or homozygote excess (D11 < 0) (Figure 1a). The 1-d.f. GOF test shows the lowest power across the spectrum of D11 values studied, while the Guo-Thompson exact test and the overall χ2-test display very similar power, especially when sample sizes are large.
On the other hand, when the frequency of the allele of interest is low, the single homozygous genotype test has power only for the detection of homozygote excess, unless the sample size is very large (Figure 1b). Again, the Guo-Thompson exact test and overall χ2-test show similar power. Both tests have lower power than the 1-d.f. GOF test, which in turn is lower than, but close to, the power of the single homozygous genotype test.
An application:
One of the problems for microsatellite genotyping is extreme preferential amplification (EPA). For microsatellite heterozygotes, the shorter fragment size generally amplifies better than the larger fragment. In extreme cases it can be difficult to distinguish the longer allele from background noise leading to the overrepresentation of homozygotes for the shorter alleles (Demers et al. 1995). Consequently, the nonrandom genotyping errors will affect the subsequent analyses using these genotyping results.
For illustration, we applied the proposed single homozygous genotype test to genotype data for the MogCA microsatellite marker from 47 unrelated individuals of Northern European descent to illustrate the usefulness of the test when EPA is a problem. The subjects studied are the grandparents of 13 CEPH families that have been extensively used in human genetic studies. MogCA is a microsatellite polymorphism located in the extended class I human leukocyte antigen (HLA) region on chromosome six. Nine distinct MogCA alleles were found in this data set. Details of the microsatellite typing can be found in Martin et al. (1998).
Previous experience with this marker along with a significant overall test of HWE proportions suggested possible preferential amplification problems. Single homozygous genotype testing applied to the data revealed highly significant overrepresentation for homozygotes of five of the nine MogCA alleles (MogCA*122, -*132, -*134, -*136, and -*148). It provides valuable information that was not available from the overall test. Individuals were then retyped using a PCR protocol designed to compensate for preferential amplification. After retyping, only one unadjusted homozygote deviation remained marginally significant (for the MogCA*136 allele).
Discussion:
With the increasing amount of genetic data and the fact that the assumption of HWE has been built into many disease models and subsequent genetic data analyses, testing for HWE proportions has become an important quality control step for genetic data. Deviation from the HWE proportions suggests that at least one of the standard underlying assumptions for the test (nonoverlapping generations, large population size with random mating, no mutation, no migration, and no selection) may be violated.
Genotyping error, however, is a primary suspect in any observed deviations from HWE proportions; these may be genotype specific and not necessarily detected in an overall test. If genotyping error is ruled out, other possibilities such as admixture should be investigated. Of more interest in a population genetics setting are situations where heterozygote advantage may have shaped allele and genotype frequency distributions, resulting in a reduced frequency of specific homozygotes, for example, with certain HLA genes. The single homozygous genotype test developed expands our range of options for testing deviations from HWE proportions. The test can be applied to data from any genetic system. It is especially powerful for highly polymorphic loci, e.g., microsatellite loci, and HLA genes in population and disease studies.
Microsatellite polymorphisms are among the most commonly used markers in genetic analyses (Ellegren 2000). Unlike biallelic SNPs, microsatellite polymorphisms tend to be highly polymorphic. While microsatellites provide an abundant and cost-effective source of genetic markers, several aspects of their typing can create various kinds of bias in downstream genetic analyses.
As shown in the application example, the single homozygous genotype test described in this research provides a powerful tool for detecting microsatellite EPA problems. Another closely related microsatellite genotyping problem is allele dropout (Rodriguez et al. 2001), in which a certain allele simply does not amplify irrespective of allele length. This could be caused by the variation in the sequence to which the PCR primers anneal, low concentration, or low quality of template DNA. Allele dropout can also result in an artificial increase of specific homozygous genotypes. Again, these nonrandom genotyping errors will influence the subsequent analyses based on these genotyping results. Problems due to EPA or allele dropout, when detected, can often be alleviated by retyping the microsatellite using a modified PCR reaction. An excess of homozygotes primarily for the shorter alleles and a deficiency of heterozygotes between long and short alleles suggest possible EPA problems and the researcher can manually examine the genotyping traces or retype individuals at the locus using a PCR program designed to reduce the amplification difference between long and short alleles (Rodriguez et al. 2001). To detect and correct potential EPA and allele dropout problems, properly checking HWE proportions becomes crucial, especially when there are excesses of specific homozygous genotypes (Gomes et al. 1999).
In addition to its application to microsatellite genotyping, the proposed single homozygous genotype test is well suited to detect deviations from HWE proportions for other types of highly polymorphic loci. For example, the study of deviation from HWE proportions can be utilized in the detection of selection acting on a polymorphic genetic region, such as the HLA region (e.g., Chen et al. 1999). It can also be applied to patient data to detect genotype-specific effects on disease risk. When an overall test for Hardy-Weinberg is significant, for markers of any type, additional information about the specific genotypes responsible for the deviation can aid either in the detection and resolution of genotyping errors or in the identification of specific genotypes on which selection may be acting.
Acknowledgments
This work was supported by grants AI49213 (G.T. and R.S.) and GM 35326 (G.T. and K.M.) from the National Institutes of Health and DE-FG02-00ER45828 (R.S.) from the U.S. Department of Energy.
References
- Bailey, N. T. J., 1961 Introduction to the Mathematical Theory of Genetic Linkage. Oxford University Press, Oxford.
- Chen, J. J., and G. Thomson, 1999. The variance for the disequilibrium coefficient in the individual Hardy-Weinberg test. Biometrics 55 1269–1272. [DOI] [PubMed] [Google Scholar]
- Chen, J. J., J. A. Hollenbach, E. A. Trachtenberg, J. J. Just, M. Carrington et al., 1999. Hardy-Weinberg testing for HLA class II (DRB1, DQA1, DQB1, and DPB1) loci in 26 human ethnic groups. Tissue Antigens 54 533–542. [DOI] [PubMed] [Google Scholar]
- Demers, D. B., E. T. Curry, M. Egholm and A. C. Sozer, 1995. Enhanced PCR amplification of VNTR locus D1S80 using peptide nucleic acid (PNA). Nucleic Acids Res. 23 3050–3055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellegren, H., 2000. Heterogeneous mutation processes in human microsatellite DNA sequences. Nat. Genet. 24 400–402. [DOI] [PubMed] [Google Scholar]
- Elston, R. C., and R. Forthofer, 1977. Testing for Hardy-Weinberg equilibrium in small samples. Biometrics 33 536–542. [Google Scholar]
- Emigh, T. H., 1980. A comparison of tests for Hardy-Weinberg equilibrium. Biometrics 36 627–642. [PubMed] [Google Scholar]
- Gomes, I., A. Collins, C. Lonjou, N. S. Thomas, J. Wilkinson et al., 1999. Hardy-Weinberg quality control. Ann. Hum. Genet. 63 535–538. [DOI] [PubMed] [Google Scholar]
- Guo, S. W., and E. A. Thompson, 1992. Performing the exact test of Hardy-Weinberg proportion for multiple alleles. Biometrics 48 361–372. [PubMed] [Google Scholar]
- Hernández, J. L., and B. S. Weir, 1989. A disequilibrium coefficient approach to Hardy-Weinberg testing. Biometrics 45 53–70. [PubMed] [Google Scholar]
- Li, C. C., 1955 Population Genetics. University of Chicago Press, Chicago.
- Louis, E. J., and E. R. Dempster, 1987. An exact test for Hardy-Weinberg and multiple alleles. Biometrics 43 805–811. [PubMed] [Google Scholar]
- Martin, M. P., A. Harding, R. Chadwwick, M. Kronick, M. Cullen et al., 1998. Characterization of 12 microsatellite loci of the human MHC in a panel of reference cell lines. Immunogenetics 47(2): 131–138. [DOI] [PubMed] [Google Scholar]
- Rodriguez, S., G. Visedo and C. Zapata, 2001. Detection of errors in dinucleotide repeat typing by nondenaturing electrophoresis. Electrophoresis 22 2656–2664. [DOI] [PubMed] [Google Scholar]
- Sebetan, I. M., and H. A. Hajar, 1997. HLA DQa genotype and allele frequencies in Qatari population. Forensic Sci. Int. 90 11–15. [DOI] [PubMed] [Google Scholar]
- Smith, C. A. B., 1986. Chi-squared tests with small numbers. Ann. Hum. Genet. 50 163–167. [DOI] [PubMed] [Google Scholar]