The structure of scientific collaboration networks

Abstract

The structure of scientific collaboration networks is investigated. Two scientists are considered connected if they have authored a paper together and explicit networks of such connections are constructed by using data drawn from a number of databases, including MEDLINE (biomedical research), the Los Alamos e-Print Archive (physics), and NCSTRL (computer science). I show that these collaboration networks form “small worlds,” in which randomly chosen pairs of scientists are typically separated by only a short path of intermediate acquaintances. I further give results for mean and distribution of numbers of collaborators of authors, demonstrate the presence of clustering in the networks, and highlight a number of apparent differences in the patterns of collaboration between the fields studied.

A social network is a collection of people, each of whom is acquainted with some subset of the others. Such a network can be represented as a set of points (or vertices) denoting people, joined in pairs by lines (or edges) denoting acquaintance. One could, in principle, construct the social network for a company or firm, for a school or university, or for any other community up to and including the entire world.

Social networks have been the subject of both empirical and theoretical study in the social sciences for at least 50 years (1–3), partly because of inherent interest in the patterns of human interaction, but also because their structure has important implications for the spread of information and disease. It is clear, for example, that variation in just the average number of acquaintances that individuals have (also called the average degree of the network) might substantially influence the propagation of a rumor, a fashion, a joke, or this year's flu.

A famous early empirical study of the structure of social networks, conducted by Stanley Milgram (4), asked test subjects, chosen at random from a Nebraska telephone directory, to get a letter to a target subject in Boston, a stockbroker friend of Milgram's. The instructions were that the letters were to be sent to their addressee (the stockbroker) by passing them from person to person, but that they could be passed only to someone whom the passer knew on a first-name basis. Because it was not likely that the initial recipients of the letters were on a first-name basis with a Boston stockbroker, their best strategy was to pass their letter to someone whom they felt was nearer to the stockbroker in some sense, either social or geographical: perhaps someone they knew in the financial industry, or a friend in Massachusetts.

A moderate number of Milgram's letters did eventually reach their destination, and Milgram discovered that the average number of steps taken to get them there was only about six, a result that has since passed into folklore and was immortalized by John Guare in the title of his 1990 play, Six Degrees of Separation (5). Although there were certainly biases present in Milgram's experiment—letters that took a longer path were perhaps more likely to get lost or forgotten, for instance (6)—his result is usually taken as evidence of the “small-world hypothesis,” that most pairs of people in a population can be connected by only a short chain of intermediate acquaintances, even when the size of the population is very large.

Milgram's work, although cleverly conducted and in many ways revealing, does not, however, tell us much about the detailed structure of social networks, data that are crucial to the understanding of information or disease propagation. Many other studies have addressed this problem (discussions can be found in refs. 1–3). Foster et al. (7), Fararo and Sunshine (8), and Moody and White (9), for instance, all conducted studies of friendship networks among middle- or high-school students, Bernard et al. (10) did the same for communities of Utah Mormans, Native Americans, and Micronesian islanders, and there are many other examples to be found in the literature. Surveys or interviews were used to determine friendships.

Although these studies directly probe the structure of the relevant social network, they suffer from two substantial shortcomings that limit their usefulness. First, the studies are labor intensive, and the size of the network that can be mapped is therefore limited—typically to a few tens or hundreds of people. Second, these studies are highly sensitive to subjective bias on the part of interviewees; what is considered to be an “acquaintance” can differ considerably from one person to another. To avoid these issues, a number of researchers have studied networks for which there exist more numerous data and more precise definitions of connectedness. Examples of such networks are the electric power grid (3, 11), the Internet (12, 13), and the pattern of air traffic between airports (14). These networks, however, suffer from a different problem: although they may loosely be said to be social networks in the sense that their structure in some way reflects features of the society that built them, they do not directly measure actual contact between people. Many researchers, of course, are interested in these networks for their own sake, but to the extent that we want to know about human acquaintance patterns, power grids and computer networks are a poor proxy for the real thing.

Perhaps the nearest that studies of this kind have come to looking at a true acquaintance network is in studies of the network of movie actors (11, 14). In this network, which has been thoroughly documented and contains nearly half a million people, two actors are considered connected if they have been credited with appearance in the same film. However, although this is genuinely a network of people, it is far from clear that the appearance of two actors in the same movie implies that they are acquainted in any but the most cursory fashion, or that their acquaintance extends off screen. To draw conclusions about patterns of everyday human interaction from the movies would, it seems certain, be a mistake.

In this paper, I present a study of a genuine network of human acquaintances that is large—containing over a million people—and for which a precise definition of acquaintance is possible. That network is the network of scientific collaboration, as documented in the papers scientists write.

Scientific Collaboration Networks

I study networks of scientists in which two scientists are considered connected if they have coauthored a paper. This seems a reasonable definition of scientific acquaintance: most people who have written a paper together will know one another quite well. It is a moderately stringent definition, since there are many scientists who know one another to some degree but have never collaborated on the writing of a paper. Stringency, however, is not inherently a bad thing. A stringent condition of acquaintance is perfectly acceptable, provided, as in this case, that it can be applied consistently.

I have constructed collaboration graphs for scientists in a variety of fields. The data come from four databases: MEDLINE (which covers published papers on biomedical research), the Los Alamos e-Print Archive (preprints primarily in theoretical physics), SPIRES (published papers and preprints in high-energy physics), and NCSTRL (preprints in computer science). In each case, I have examined papers that appeared in a 5-year window, from 1995 to 1999 inclusive. The sizes of the databases range from 2 million papers for MEDLINE to 13,000 for NCSTRL.

That some of the databases used contain unrefereed preprints should not be regarded negatively. Although unrefereed preprints may be of lower average scientific quality than papers in peer-reviewed journals, as an indicator of social connection, they are every bit as good as their refereed counterparts.

The idea of studying collaboration patterns by using data drawn from the publication record is not new. There is a substantial body of literature in information science dealing with coauthorship patterns (15–19) and cocitation patterns (20–22) (i.e., connections between authors established via the citation of their works in the same literature). However, to our knowledge, no detailed reconstruction of an actual collaboration network has previously been attempted. Indeed, the nearest thing to such a reconstruction comes not from information science at all, but from the mathematics community, within which the concept of the Erdös number has a long history. Paul Erdös was an influential but itinerant Hungarian mathematician, who apparently spent a large portion of his later life living out of a suitcase and writing papers with those of his colleagues willing to give him room and board (23). He published at least 1,401 papers during his life, more than any other mathematician in history, except perhaps Leonhard Euler. The Erdös number measures a mathematician's proximity, in bibliographical terms, to the great man. Those who have published a paper with Erdös have an Erdös number of 1. Those have published with a coauthor of Erdös have an Erdös number of 2, and so on. An exhaustive list exists of all mathematicians with Erdös numbers of 1 and 2 (24).

In addition to distance between authors, there are many other interesting quantities to be measured on collaboration networks, including the number of collaborators of scientists, the numbers of papers they write, and the degree of “clustering,” which is the probability that two of a scientist's collaborators have themselves collaborated. All of these quantities and several others are considered in this paper.

Results

Table 1 gives a summary of some of the results of the analysis of databases described in the previous section. In addition to results for the four complete databases, results are also given for three subject-specific subsets of the Los Alamos Archive, covering astrophysics (denoted astro-ph), condensed matter physics (cond-mat), and theoretical high-energy physics (hep-th). In this section, I highlight some of these results and discuss their implications.

Table 1.

Summary of results of the analysis of seven scientific collaboration networks

	MEDLINE	Los Alamos e-Print Archive				SPIRES	NCSTRL
		Complete	astro-ph	cond-mat	hep-th
Total papers	2,163,923	98,502	22,029	22,016	19,085	66,652	13,169
Total authors	1,520,251	52,909	16,706	16,726	8,361	56,627	11,994
First initial only	1,090,584	45,685	14,303	15,451	7,676	47,445	10,998
Mean papers per  author	6.4 (6)	5.1 (2)	4.8 (2)	3.65 (7)	4.8 (1)	11.6 (5)	2.55 (5)
Mean authors  per paper	3.754 (2)	2.530 (7)	3.35 (2)	2.66 (1)	1.99 (1)	8.96 (18)	2.22 (1)
Collaborators  per author	18.1 (1.3)	9.7 (2)	15.1 (3)	5.86 (9)	3.87 (5)	173 (6)	3.59 (5)
Cutoff zc	5,800 (1,800)	52.9 (4.7)	49.0 (4.3)	15.7 (2.4)	9.4 (1.3)	1,200 (300)	10.7 (1.6)
Exponent τ	2.5 (1)	1.3 (1)	0.91 (10)	1.1 (2)	1.1 (2)	1.03 (7)	1.3 (2)
Size of giant  component	1,395,693	44,337	14,845	13,861	5,835	49,002	6,396
First initial only	1,019,418	39,709	12,874	13,324	5,593	43,089	6,706
As a percentage	92.6 (4)%	85.4 (8)%	89.4 (3)	84.6 (8)%	71.4 (8)%	88.7 (1.1)%	57.2 (1.9)%
Second largest  component	49	18	19	16	24	69	42
Mean distance	4.6 (2)	5.9 (2)	4.66 (7)	6.4 (1)	6.91 (6)	4.0 (1)	9.7 (4)
Maximum distance	24	20	14	18	19	19	31
Clustering coefficient C	0.066 (7)	0.43 (1)	0.414 (6)	0.348 (6)	0.327 (2)	0.726 (8)	0.496 (6)

Numbers in parentheses are standard errors on the least significant figures. 

Number of Authors.

Estimating the true number of distinct authors in a database is complicated by two problems. First, two authors may have the same name. Second, authors may identify themselves in different ways on different papers, e.g., by using first initial only, by using all initials, or by using full name. To estimate the size of the error introduced by these effects, all analyses reported here have been carried out twice. The first time, all initials of each author are used. This will rarely confuse two different authors for the same person (although this will still happen occasionally) but sometimes misidentifies the same person as two different people, thereby overestimating the total number of authors. The second analysis is carried out using only the first initial of each author, which will ensure that different publications by the same author are almost always identified as such, but will with some regularity confuse distinct authors for the same person. Thus these two analyses give upper and lower bounds on the number of authors and also give an indication of the expected precision of many of our other measurements. In Table 1, both estimates of the number of authors for each database are quoted. For most other quantities, only an error estimate based on the separation of the upper and lower bounds is quoted.

Mean Papers per Author and Authors per Paper.

Authors typically wrote about four papers in the 5-year period covered by this study. The average paper had about three authors. Notable exceptions are in theoretical high-energy physics and computer science, in which smaller collaborations are the norm (an average of two people), and the SPIRES high-energy physics database, with an average of nine authors per paper. The reason for this last impressive figure is that the SPIRES database contains data on experimental as well as theoretical work. High-energy experimental collaborations can run to hundreds or thousands of people, the largest author list in the SPIRES database giving the names of a remarkable 1,681 authors on a single paper.

Number of Collaborators.

The striking difference in collaboration patterns in high-energy physics is highlighted further by the results for the average number of collaborators of an author. This is the average total number of people with whom a scientist collaborated during the period of study—the average degree, in the graph theorist's language. For purely theoretical databases, such as the hep-th subset of the Los Alamos Archive (covering high-energy physics theory) and NCSTRL (computer science), this number is low, on the order of four. For partly or wholly experimental databases [condensed matter physics and astrophysics at Los Alamos and MEDLINE (biomedicine)], the degree is significantly higher, as high as 18 for MEDLINE. But high-energy experiment easily takes the prize, with an average of 173 collaborators per author.

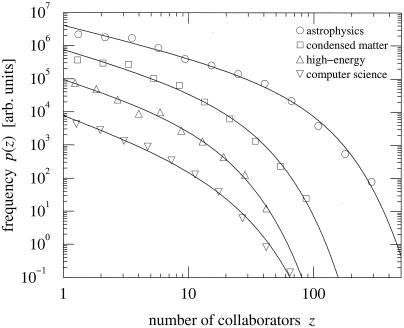
There is more to the story of numbers of collaborators, however. In Fig. 1, histograms of the numbers of collaborators of scientists in four of the smaller databases are shown. There has been a significant amount of recent discussion of this distribution for a variety of networks in the literature. A number of authors (12, 13) have pointed out that if one makes a similar plot for the number of connections (or “links”) z to or from sites on the World Wide Web, the resulting distribution closely follows a power law: P(z)≈z^−τ, where τ is a constant exponent with (in that case) a value of about 2.5. Barabási and Albert have suggested (25) that a similar power-law result may apply to all or at least most other networks of interest, including social networks. Others have presented a variety of evidence to the contrary (14). My data do not follow a power-law form perfectly. If they did, the curves in Fig. 2 would be straight lines on the logarithmic scales used. However, these data are well fitted by a power-law form with an exponential cutoff:

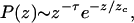1

where τ and z_c are constants. Fits to this form are shown as the solid lines in Fig. 2. In each case, the fit has an R² of better than 0.99 and P values for both power-law and exponential terms of less than 10⁻³ (except for the “all-initials” version of the MEDLINE network, for which the exponential term has P = 0.17, indicating that this distribution is moderately well fit by a pure power-law form).

Figure 1.

Histograms of the number of collaborators of scientists in four of the databases studied here. The solid lines are least-squares fits to Eq. 1.

Figure 2.

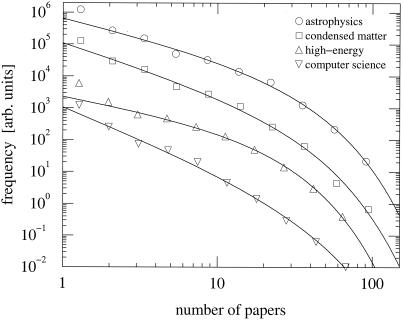
Histograms of the number of papers written by scientists in four of the databases. As with Fig. 1, the solid lines are least-squares fits to Eq. 2.

This form is commonly seen in physical systems and suggests an underlying degree distribution that follows a power law, but with some imposed constraint that places a limit on the maximum value of z. One possible explanation of this cutoff in the present case is that it arises as a result of the finite (5-year) window of data used. If this were the case, we would expect the cutoff to increase with increasing window size. But even in the (impractical) limit of infinite window size, a cutoff would still be imposed by the finite working lifetime of a professional scientist (about 40 years).

The values of τ and z_c are given in the table for each database. The value of the cutoff size, z_c, varies considerably. For the mostly theoretical condensed matter, high-energy theory, and computer science databases, it takes small values on the order of 10, indicating that theorists rarely had more than this many collaborators during the 5-year period. In other cases, such as SPIRES and MEDLINE, it takes much larger values. In the case of SPIRES, this is probably again because of the presence of very large experimental collaborations in the data. MEDLINE is more interesting. There are few very large collaborations in the MEDLINE database, and yet there are a small number of individuals with very large numbers of collaborators. How does this arise? One possibility is that it is the result of the practice in the biomedical research community of laboratory directors signing their name to all (or most) papers emerging from their laboratories. One can well imagine that, with some individuals directing very large laboratories, this could generate authors with a very high apparent number of collaborators. [It is possible that a similar mechanism is at work in the SPIRES data also.] This hypothesis could be checked by verifying whether the individuals with the largest numbers of collaborators are indeed lab directors or principal investigators and might make an interesting topic for further study.

The exponent τ of the power-law distribution is also interesting. We note that in all of the “hard sciences,” this exponent takes values close to 1. In the MEDLINE (biomedicine) database, however, its value is 2.5, similar to that noted for the World Wide Web. The value τ = 2 forms a dividing line between two fundamentally different behaviors of the network. For τ < 2, the average properties of the network are dominated by the few individuals who have a large number of collaborators, whereas networks with τ > 2 are dominated by the “little people”—those with few collaborators. Thus, one finds that in biomedical research, highly connected individuals do not determine the average characteristics of their field, despite their names appearing on a lot of papers. In physics and computer science, on the other hand, it appears that such individuals do determine these characteristics.

In Fig. 2, histograms are shown of the number of papers that authors have written in the same four databases. As the figure shows, the distribution of papers follows a similar form to the distribution of collaborators. The solid lines are again fits to Eq. 1 and again match the data well in all cases. This form may be regarded as a generalization of the well-known Lotka law of scientific productivity, which states that the distribution of numbers of papers written should follow a power law (16, 26). The clear exponential cutoff seen in the distribution is again presumably a result of the finite time window used in this study. It would be interesting to test this hypothesis by varying the window size, although a thorough test may have to wait until more years of data are available; most of the databases studied here have not been in existence long enough to give good statistics on this point. The SPIRES database, which has been in existence for more than a quarter of a century, is an exception and might make an interesting case study (27).

The Giant Component.

In all social networks, there is the possibility of a percolation transition (28). In networks with very small numbers of connections between individuals, all individuals belong only to small islands of collaboration or communication. As the total number of connections increases, however, there comes a point at which a giant component forms—a large group of individuals who are all connected to one another by paths of intermediate acquaintances. It appears that all of the databases considered here are connected in this sense. Measuring the size of groups of connected authors in each database, we find (see Table 1) that in most of the databases, the largest such group occupies around 80 or 90% of all authors: almost everyone in the community is connected to almost everyone else by some path (probably many paths) of intermediate coauthors. In high-energy theory and computer science, the fraction is smaller but still more than half the total size of the network. (These two databases may, it appears, give a less complete picture of their respective fields than the others, because of the existence of competing databases with overlapping coverage. The small size of the giant component may in part be attributable to this.)

I have also calculated the size of the second-largest group of connected authors for each database. In each case, this group is far smaller than the largest. This is a characteristic signature of networks that are well inside the percolating regime. In other words, it appears that scientific collaboration networks are not on the borderline of connectedness—they are very highly connected and in no immediate danger of fragmentation. This is a good thing. Science would probably not work at all if scientific communities were not densely interconnected.

Average Degrees of Separation.

I have calculated exhaustively the minimum distance, in terms of numbers of links in the network, between all pairs of scientists in our databases for whom a connection exists. I find that the typical distance between a pair of scientists is about six; there are six degrees of separation in science, just as there are in the larger world of human acquaintance. Even in very large communities, such as the biomedical research community documented by MEDLINE, it takes an average of only about six steps to reach a randomly chosen scientist from any other, of the more than one million who have published. We conjecture that this has a profound effect on the way the scientific community operates. Despite the importance of written communication in science as a document and archive of work carried out, and of scientific conferences as a broadcast medium for summary results, it is probably safe to say that the majority of scientific communication still takes place by private conversation. The existence of a large giant component, as discussed in the previous section, allows news of important discoveries and scientific information to reach most members of the network via such private conversations, and clearly information can circulate far faster in a world where the typical separation of two scientists is six than it can in one where it is a thousand or a million.

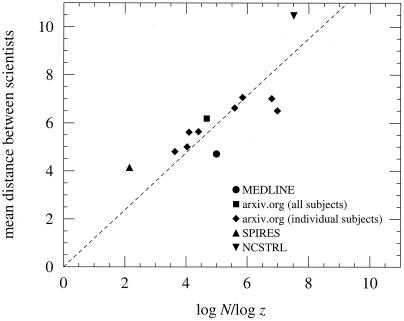
The variation of average vertex–vertex distances from one database to another also shows interesting behavior. The simplest model of a social network is the random graph—a network in which people are connected to one another uniformly at random (29). For a given number N of scientists with a given mean number z of collaborators, the average vertex–vertex distance on a random graph varies as the logarithm of N according to log N/log z. Social networks are measurably different from random graphs (3), but the random graph nonetheless provides a useful benchmark against which to compare them. Watts and Strogatz (11) defined a social network as being “small” if typical distances were comparable to those on a random graph. This implies that such networks should also have typical distances that grow roughly logarithmically in N, and indeed some authors (e.g., ref. 14) have used this logarithmic growth as the defining criterion for a “small world.” In Fig. 3, the average distance between all pairs of scientists for each of the networks studied here is shown, including separate calculations for eight subject divisions of the Los Alamos Archive. In total, there are 12 points, which have been plotted against log N/log z using the appropriate values of N and z from Table 1. As the figure shows, there is a strong correlation (R² = 0.83) between the measured distances and the expected log N behavior, indicating that distances do indeed vary logarithmically with the number of scientists in a community. As far as I am aware, this is the first empirical demonstration of logarithmic variation with network size for any real social network.

Figure 3.

Average distance between pairs of scientists in the various communities, plotted against the average distance on a random graph of the same size and average coordination number. The dotted line is the best fit to the data that also passes through the origin.

Also quoted in Table 1 are figures for the maximum separation of pairs of scientists in each database, which tells us the greatest distance we will ever have to go to connect two people. This quantity is often referred to as the diameter of the network. For all of the networks examined here, it is on the order of 20; there is a chain of at most about 20 acquaintances connecting any two scientists. (This result, of course, excludes pairs of scientists who are not connected at all, as will often be the case for the 10 or 20% who fall outside the giant component.)

Clustering.

Real social networks have another important property that is absent from many network models. Real networks are clustered, meaning they possess local communities in which a higher than average number of people know one another. A laboratory or university department might form such a community in science, as might the set of researchers who work in a particular subfield. One way of probing for the existence of such clustering in network data is to measure the fraction of “transitive triples” in a network (1), also called the clustering coefficient C (11), which for a collaboration graph is the average fraction of pairs of a person's collaborators who have also collaborated with one another. Mathematically,

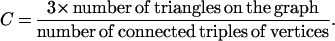2

Here a “triangle” is a trio of authors, each of whom is connected to both of the others, and a “connected triple” is a single author connected to two others. C = 1 for a fully connected graph and for a random graph, tends to zero as 1/N as the graph becomes large.

In Table 1, values of C are given for each of the networks studied here, and we can see that there is a very strong clustering effect in the scientific community: two scientists typically have a 30% or greater probability of collaborating if both have collaborated with a third scientist. A number of explanations of this result are possible. To some extent, it is certainly the result of the appearance of papers with three or more authors: such papers clearly contain trios of scientists who have all collaborated with one another. However, the values measured here cannot be entirely accounted for in this way (30) and indicate also that scientists either introduce their collaborators to one another, thereby engendering new collaborations, or perhaps that institutions bring sets of collaborators together to form a variety of new collaborations. Processes such as these have been discussed extensively in the social networks literature, in the context of structural balance within networks (1).

The MEDLINE database is interesting in that it possesses a much lower value of the clustering coefficient than the “hard science” databases. This appears to indicate that it is significantly less common in biological research for scientists to broker new collaborations between their acquaintances than it is in physics or computer science. This could again be a result of the “top-down” organization of laboratories under laboratory directors, which tends to produce “tree-like” collaboration networks, with many branches but few short loops. Such tree-like networks are known to possess low clustering coefficients.

Conclusions

The collaboration networks of scientists in biology and medicine, various subdisciplines of physics, and computer science have been analyzed, by using author attributions from papers or preprints appearing in those areas over a 5-year period from 1995 to 1999. We find a number of interesting properties of these networks. In all cases, scientific communities seem to constitute a “small world,” in which the average distance between scientists via a line of intermediate collaborators varies logarithmically with the size of the relevant community. Typically, we find that only about five or six steps are necessary to get from one randomly chosen scientist in a community to another. It is conjectured that this smallness is a crucial feature of a functional scientific community.

We also find that the networks are highly clustered, meaning that two scientists are much more likely to have collaborated if they have a third common collaborator than are two scientists chosen at random from the community. This may indicate that the process of scientists introducing their collaborators to one another is an important one in the development of scientific communities.

We have studied the distributions of both the number of collaborators of scientists and the numbers of papers they write. In both cases, we find these distributions are well fit by power-law forms with an exponential cutoff. This cutoff may be caused by the finite time window used in the study.

We find a number of significant statistical differences between different scientific communities. Some of these are obvious: experimental high-energy physics, for example, which is famous for the staggering size of its collaborations, has a vastly higher average number of collaborators per author than any other field examined. Other differences are less obvious, however. Biomedical research, for example, shows a much lower degree of clustering than any of the other fields examined. In other words, it is less common in biomedicine for two scientists to start a collaboration if they have another collaborator in common. Biomedicine is also the only field in which the exponent of the distribution of numbers of collaborators is greater than 2, implying that the average properties of the collaboration network are dominated by the many people with few collaborators, rather than, as in other fields, by the few people with many.

The work reported in this paper represents, inevitably, only a first look at the collaboration networks described. Many theoretical measures have been discussed elsewhere, in addition to the distances and clustering studied here, which reflect socially important structure in such networks. I hope that academic collaboration networks will prove a reliable and copious source of data for testing theories about such measures, as well as being interesting in their own right, especially to ourselves, the scientists whom they describe.