Energetics and Dynamics of Constrained Actin Filament Bundling

Abstract

The formation of filopodia-like bundles from a dendritic actin network has been observed to occur in vitro as a result of branching induced by Arp2/3 complex. We study both the energetics and dynamics of actin filament bundling in such a network to evaluate their relative importance in bundle formation processes. Our model considers two semiflexible actin filaments fixed at one end and free at the other, described using a normal-mode approximation. This model is studied by both Brownian dynamics and free-energy minimization methods. Remarkably, even short filaments can bundle at separations comparable to their lengths. In the dynamic simulations, we evaluate the time required for the filaments to interact and bind, and examine the dependence of this bundling time on the filament length, the distance between the filament bases, and the cross-linking energy. In most cases, bundling occurs in a second or less. Beyond a certain critical distance, we find that the bundling time increases very rapidly with increasing interfilament separation and/or decreasing filament length. For most of the cases we have studied, the energetics results for this critical distance are similar to those obtained from dynamics simulations run for 10 s, suggesting that beyond this timescale, energetics, rather than kinetic constraints, determine whether or not bundling occurs. Over a broad range of conditions, we find that the times required for bundling from a network are compatible with experimental observations.

INTRODUCTION

Actin is one of the most important proteins in eukaryotic cells. Monomeric or G-actin polymerizes to form actin filaments, or F-actin, and these filaments are involved in a wide array of cellular processes. One of the key cellular processes that is strongly actin-dependent is cell motility (1). Cells move by the extension of protrusions such as lamellipodia and filopodia caused by the polymerization of actin filaments. Lamellipodia are broad protrusions in which F-actin forms a dendritic network at the leading edge of the cell. The polymerization and depolymerization of this F-actin network are controlled by Arp2/3 complex, ADF/cofilin, capping protein, and other actin-associated proteins (2–7). In contrast, filopodia are long, fingerlike protrusions supported by actin bundles (8–11). The relative importance and differing functions of filopodia and lamellipodia in cell motility are a matter of debate within the cell biology community, but our focus in this article is the formation of bundles such as those found within filopodia.

Actin bundles are formed through cross-linking by actin bundling proteins that include fascin, α-actinin, filamin, and fimbrin (12). Although this large family of proteins are similar in function, their expression and occurrence in different organisms and tissues are quite varied. Fascin is one of the more broadly occurring bundling proteins (13–15), and has been identified in humans, mice, sea urchins, flies, and frogs (16–19). Within these organisms, it has also been demonstrated that fascins are expressed in a wide range of tissues (20,21). All fascins have two actin-binding sites that enable the cross-linking of filaments, and this bundling activity is regulated by phosphorylation (22).

The detailed structure of actin bundles can vary significantly (23). In Drosophila bristles, the long actin bundles are formed by overlapping short filaments with the protein forked, cross-linking the short filaments together (8). In Drosophila nurse cells, cytoplasmic actin bundles are formed using two actin cross-linking proteins, quail (a villin homolog) followed by fascin, where the bundles form a cage around the nucleus (18,24). In the membrane of absorptive epithelial cells, highly regular, fingerlike bundles are formed to increase the area of the apical plasma membrane (25). Fingerlike bundles, which can transduce the mechanical-electrical signals caused by sound and motion, are also found on the apical surfaces of hair cells in the inner ear (26).

Bundles formed by the reorganization of a dendritic network have recently been observed by light and electron microscopy in melanoma cells (27) and in a biomimetic system (28). In the cell study, the filopodial bundles came from the reorganization of the lamellipodial dendritic network. The filaments elongated and subsequently associated with each other at their barbed ends so that they formed cone-shaped structures, which were called Λ-precursors. GFP-vasodilator-stimulated phosphoprotein, an early marker of bundling, was associated with the Λ-precursors. The binding of fascin near the barbed ends of Λ-precursors led to bundle formation. The biomimetic study used beads coated with Arp2/3 complex in cytoplasmic extracts. Two distinct types of actin filament organization were found: comet tails or clouds displaying a dendritic array of actin filaments resulting from Arp2/3 complex, and stars with filament bundles radiating from the bead. The fascin concentration was high in the bundles, while the Arp2/3 complex and capping protein concentrations were low. Transitions between bundled and dendritic organization were caused by depletion and subsequent addition of capping protein. Both the bundled and dendritic structures were found to require Arp2/3 complex, suggesting that the bundle arose from reorganization of the dendritic network.

Based on these experiments, a model describing this reorganization was proposed, namely that “bundles are formed from a preexisting dendritic network by barbed-end elongation of actin filaments and their subsequent cross-linking into bundles” (28). To ascertain the viability of this model, it is necessary to evaluate the dynamics of filament bundling. Previous models of filament dynamics have typically regarded short filaments as rods (29,30). However, bundle formation from a network requires filament bending, and therefore the filaments must be treated as semiflexible. The inclusion of flexibility renders treatment of the dynamics considerably more complex. In this article, we develop a practical methodology for studying the dynamics and energetics of semiflexible filaments, and use it to evaluate the viability of bundle nucleation from a dendritic network and the relative importance of energetics and dynamics in determining bundle formation.

METHODS

To simulate the bundling process, we consider a simple system of two filaments of length L, each having one end fixed and the other end free. As shown in Fig. 1, these two filaments are anchored perpendicular to a rigid substrate corresponding to the network, with a separation d at their bases. We consider the cross-linker in our model to be fascin, but the formalism should apply to all filament cross-linkers. The x,y displacement vector of each filament at height z and time t is 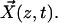There are two distinct regimes within our bundling simulations. At large separation, the filaments move only under the bending force and random thermal forces. At close contact, fascins can attach and create an attractive interaction force. The number of fascins will determine the interaction strength, which will determine the stability of a bundle. Before the bundle reaches a stable state, the filaments may detach, and it may take several cycles of attachment and detachment to form a stable bundle.

FIGURE 1.

Schematic of the bundle formation model. Both filaments have perpendicular incidence at the bottom, d is distance between the filament bases and L is total filament length. X(z) is horizontal displacement of filament at position z. The circles between the filaments represent the cross-linking proteins.

To study the dynamics and energetics of filaments and bundles, it is natural to use the bead-spring model, which treats monomers in a filament as beads and the interaction between adjacent two monomers as a stiff spring (31–33). Such a model has strong physical appeal, but the strong interactions between adjacent monomers in a filament require a very small time step and this eventually renders this model computationally impractical for timescales corresponding to the bundling experiments. For this reason, we will instead use a normal mode approach, which uses fewer variables and allows for a larger time step than the bead-spring model. Hydrodynamic interactions can be important for the dynamics of objects in viscous solutions. However, Dhont and Briels (34,35), and Tao et al. (36), have shown that they are negligible for long, rigid rods. In our study, we treat filaments much shorter than the persistence length, and therefore it is also legitimate here to ignore the hydrodynamic interactions.

Normal mode description

Our approach is to reduce the complex motion of the filaments into a sum of a small number of normal modes. Normal-mode descriptions have been used previously in describing actin filament dynamics (see for example, (37)). However, they have not, to our knowledge, been applied to our geometry of filaments fixed at their bases. We begin with the familiar equation of motion for transverse vibrations of an undamped rod (with length L) under the assumption that the transverse vibrations are much smaller than the length (38):

(1)

Here, X→ is the horizontal displacement in the (x,y) plane, ρ is the density of the rod, s is its cross-sectional area, E is its Young's modulus, and I is the bending moment, so that EI = l_pk_BT is the bending modulus, where l_p = 10 μm is the persistence length of F-actin (39–43). In the simulations described below, the transverse fluctuations are smaller than the filament length, but still large enough that an approximate evaluation of nonlinear corrections to Eq. 1 is required to test the accuracy of our findings. The correction method and the accuracy test are described below in Results.

Replacing the inertia term in Eq. 1 with the drag term and random force suitable for Brownian dynamics, and including interaction forces, we obtain

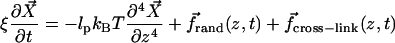(2)

Here ξ = ξ_mon/a = k_BT/D_mona is the friction coefficient per unit length, ξ_mon is the friction coefficient per monomer, a = 27 Å is the filament length per monomer, D_mon = 4 × 10⁹ Ų/s is the in vitro monomer diffusion constant, 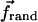is the random thermal force per unit length, and is the interaction force per unit length induced by cross-linkers. Our value of D is taken toward the lower end of the range of measured values (44,45). It is generally believed that in vivo values of D are approximately an order-of-magnitude smaller than the in vitro values. This would lead to an increase of the bundling time inversely proportional to the decrease in D.

Equation 2 can be described by a complete set of normal-mode solutions, X_N(z). In this notation the time-dependent displacement vector in the x,y plane can be written as

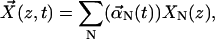(3)

where 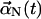is the time-dependent part and X_N(z) is the position-dependent part. To obtain the X_N(z), we note that by definition they satisfy the equation

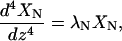(4)

with the boundary conditions X_N(0) = 0, dX_N/dz|₀ = 0, and d²X_N/dz²|_L = 0. The solutions of Eq. 4 are

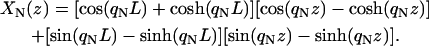(5)

The values of q_N are determined by the condition cos(q_NL) cosh(q_NL) + 1 = 0, which follows from the boundary conditions at L. The resulting values of q_N for the first four modes are: q₁ = 1.875/L, q₂ = 4.694/L, q₃ = 7.855/L, and q₄ = 10.990/L. Although any normalization of the X_N could be used if appropriate factors are included in the 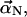we choose the normalization of Eq. 5 (i.e., a prefactor of unity before the cosine factors) because it gives the simplest calculations. Fig. 2 shows the thermal average displacement of the first four normal modes for a filament with length 1 μm. As is typical for eigenvalue equations such ours, each increase of 1 in N adds another mode to the displacement profile. The displacements decrease very rapidly with increasing N. Even though our filament profiles are fully three-dimensional, the subunits move only in the plane perpendicular to the filament orientation. The type of model used here will be accurate if the X-displacements are sufficiently small, and if enough normal modes are included. The extent to which these criteria are satisfied is discussed below.

FIGURE 2.

Thermal root-mean-square displacement of the first four normal modes for a filament of length 1 μm.

Dynamics

Our equation of motion for 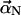has a deterministic component from the filament stiffness and the filament-filament interactions, and a random component from thermal forces. The equation of motion obtained from Eq. 2 for a very small time step Δt is

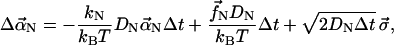(6)

where the first term comes from the elastic restoring force, the second term comes from the interfilament interactions, and the third term comes from the random forces (see Appendix). Here each component of 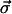has a normal distribution, 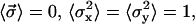where

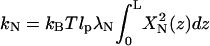(7)

is the effective spring constant for normal mode N, and

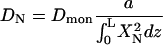(8)

is the corresponding diffusion constant. In the second term in Eq. 6,

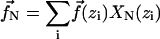(9)

is the component of interfilament force acting on the N^th normal mode, and is the force due to interfilament forces at position z_i, where the cross-linker attaches.

In the absence of interfilament interactions, the time dependence of the N^th mode coefficient vector 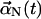is the same as that of a particle in a harmonic potential well. One could simulate the motion of each mode using Eq. 6 to obtain the motion of the filament, as a sum of several modes. However, this procedure requires too short a time step to be practical, and for this reason we instead use a Green's function method with a variable time step. If the normal-mode coefficient has value at time t, the Green's function gives the probability density that the normal-mode coefficient has value at time t + Δt. The Green's function is (14)

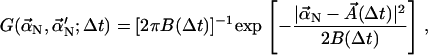(10)

where

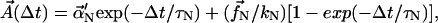(11)

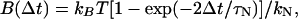(12)

and

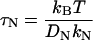(13)

is the relaxation time for the N^th normal mode. Equations 11 and 12 are obtained from the results and respectively (46). The bending energy for each normal mode is

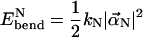(14)

and the total bending energy is

(15)

From the Green's function, we have enough information to calculate the updated value of each normal-mode coefficient as

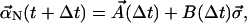(16)

where, as above, each component of 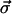has a normal distribution with variance 1. This Green's function approach allows the use of much larger time steps because it is exact for zero or constant force.

Cross-linking energy

The attractive interaction between the filaments is assumed to result from a cross-linking protein such as fascin. The interaction acts only between a subset of the filament subunits corresponding to the cross-linker binding sites. Its distance dependence can be approximated (47) as

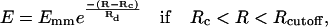(17)

where E_mm < 0 is the minimum value of the potential, R is the distance between the two subunits, R_c is the contact distance (the closest allowed distance), R_cutoff is the cutoff distance, and R_d is the decay length. The potential is zero if R > R_cutoff and infinity if R < R_c. For simplicity, and because the interaction between F-actin and fascin has a significant electrostatic component, we choose a similar functional form here. To make the potential smooth at the contact distance, we use a slightly modified interaction, which includes separate attractive and repulsive parts:

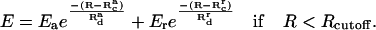(18)

The force calculated from this energy function is included in the simulations via the 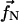coefficient in A(Δt), given above in Eq. 10. As for the binding sites, since the actin filament has a periodicity of 13 monomers, the minimum spacing between two adjacent fascins in a bundle should also be 13 monomers, or ∼35 nm (26). We use this value for the spacing between subunits that interact. Then the total cross-linking energy is

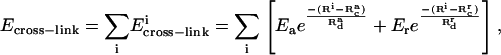(19)

where Rⁱ is the intersubunit separation at the i^th binding site. We did not consider the effect of varying the cross-linker concentration in our model. In our calculations the cross-linker will attach immediately when two filaments are close enough, so that in effect we are assuming a saturating concentration of cross-linker.

Simulation procedure

Equilibrium energetics

The equilibrium energetics describes the state reached after the two filaments have moved for an infinitely long time. The total free energy of the bundled state relative to the unbundled state is ΔF_tot = ΔE_bend + E_cross-link – TΔS, where ΔS = −[13.2 + 3 ln(L/1 μm)]k_B is the difference in the filament configurational entropy (see Appendix), the bending energy ΔE_bend is given by Eq. (15), and E_cross-link is given by Eq. 19. The value ΔF_tot is negative if the bundled state is preferred. Since ΔF_tot includes several competing contributions, there are many local minima in the bundling process. To navigate this complex free energy surface we use a combination of Monte Carlo and steepest-descent methods, based on ΔF_tot. We choose a range of initial values for the normal-mode coefficients so that there are between two and seven cross-linking points (fascins) between the filaments. At first, we use a Monte Carlo approach to scan roughly for the global minimum. For each step, we calculate the new values of the normal-mode coefficients using where each component of 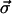has a normal distribution with variance 1, 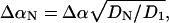and Δα = 0.02 Å. Then we choose a random number from a uniform distribution on [0, 1]. We accept the update if the random number is smaller than 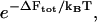where T = 300 K, and reject it otherwise. We update and record the normal-mode coefficients each time the free energy is lowered, and stop the Monte Carlo run when the free energy is not lowered for 10⁹ steps. Finally, we use these Monte Carlo optimized normal-mode coefficients as initial coefficients for the steepest-descent approach. Here we update the normal-mode coefficients using just the deterministic part of Eq. 6. We use a fictitious time step of Δt = Δt₀/(n + 1), where n is the number of cross-links and 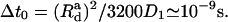This gives a typical spatial step of 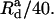We consider the system to have reached equilibrium if the free energy change between two adjacent steps is smaller than 10⁻⁸ k_BT. Because ΔS is independent of d, and ΔE_bend increases with d for fixed L, ΔF_tot will do so also. On the other hand, it is negative for very small d. Therefore there will be a maximum critical distance d_c for bundling, at which ΔF_tot = 0, for a given L. If the filament distance exceeds d_c, no stable bundle can be formed. To estimate how long it will take to form a stable bundle for a given filament length and distance, we need to simulate the dynamics of bundling, as discussed below.

Dynamics

Our dynamics simulations are based on the stochastic position updates given by Eq. 16 at a temperature of T = 300 K. The initial conformation of the filament is selected by taking random points on a thermal distribution for each normal mode. During the simulation, the bundle will be formed and broken several times until enough fascins attach to form a stable bundle with ΔF_tot < 0. We define the bundling time as the point at which ΔF_tot first becomes negative. For most values of the parameters, we run the simulation 100 times, which gives a statistical error of ∼10% in the bundling time. For values of L and d near the bundling threshold, the runs are much more computationally demanding, and here we have used fewer runs. The smallest number of runs used was five, which would lead to an error of ∼50% in the bundling time. However, this is in a range where the bundling time is varying very rapidly as a function of d and L, so the effect of the error on the critical values of d and L is still small.

Parameter justification

An important consideration in our model is the number of normal modes that we use. To choose this number, we simulated and compared the mean times for a 1-μm filament to reach a boundary 0.25 μm away, employing between two and eight normal modes. We found that four normal modes was sufficient (resulting in an error of <1%) and used this number for all subsequent simulations.

For the cross-linking potential parameters (Eq. 18), we take 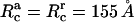and R_cutoff = 180 Å, as in Yu and Carlsson (47). We take 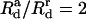as is commonly done for Morse potentials of the type we are using. By fitting the potential to that in Yu and Carlsson (47), which had a decay length of 7 Å, we obtain Å and 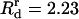Å. Values of E_a and E_r were calculated by fixing the minimum to be at r = R_c and the minimum value of the energy to be E₀, where E₀ = k_BT ln K_d and K_d is the dissociation constant. The K_d values of cross-linking proteins, such as fascin and α-actinin (22,48,49), range from 0.1 μM to 6.7 μM. These correspond to E₀ in the range −15 k_BT to −10 k_BT. To expand the applicability of our model and include a wider range of cross-linkers, we will consider the two different values −15 k_BT and −7.5 k_BT for E₀.

Our Green's function formalism allows the use of a variable time step. If the two filaments are far away from each other, there is no cross-linking interaction and we can use a large time step on the order of 10⁻⁷ s. If, however, the two filaments are close to each other, we need to monitor for cross-linking and therefore use a smaller time step. If there is cross-linking, we choose a time step which is determined by the number of cross-linking sites we found, since stronger interaction forces require smaller time steps. We allow the maximum displacement from the thermal random force, bending force, and cross-linking force to be at most 10% of the decay length of the interaction. This gives, for example, a time step of ∼10⁻¹⁰ s for a 0.6-μm filament with two cross-linking points.

The Green's function formalism and normal mode analysis significantly improve the simulation efficiency. For bead-spring models, the strong interactions between adjacent monomers limit the time step to ∼10⁻¹² s. In addition, the CPU time per time step is much larger. Altogether, the Green's function and normal mode analysis accelerate the computation by a factor of 10³–10⁷. One could envision coarse-graining the bead-spring model to obtain a block model, where groups of subunits move as single entities. However, in this case the size of these groups would be limited to 13 subunits, the repeat unit which contains a single fascin binding site. This improvement still would not achieve the efficiency of the normal-mode approach.

RESULTS

All of our calculations were performed using two representative values for the cross-linking energy, E₀ = −7.5 k_BT and E₀ = −15 k_BT. Fig. 3 shows the mean bundling time and first contact time as functions of d, for two filament lengths. The first contact time is defined as the first time when the center-to-center distance between the filaments at any of the possible attachment positions is less than R_cutoff, so that a cross-linking interaction occurs. For E₀ = −7.5 k_BT, the bundling time is close to the first contact time for short distances, but is much larger than the first contact time for large distances. This means that for short distances d, the filaments contact and then form bundles quickly—the initial bundle does not dissociate. For long distances, the metastable bundle will be broken and reformed many times before a stable bundle forms. As Fig. 3 shows, larger values of d increase the time required to form a stable bundle; smaller values of L have the same effect (not shown). The bundling time increases very abruptly with d. This occurs not only because the first contact time varies sharply with d, but also because for larger d, it takes longer to adjust the filament shape to allow more fascins to attach. For E₀ = −15 k_BT, the bundling time is always close to the first contact time in our range of L and d. This means that the interaction is so strong that once two filaments are held together by a cross-linker, they will stay together long enough for the second crosslinker to attach and form a stable bundle. We find that the time between the first cross-linker attachment and the second cross-linker attachment is very short compared to the first contact time.

FIGURE 3.

Bundling time for E₀ = −7.5 k_BT (open triangles) and E₀ = −15 k_BT (open circles), and first contact time (open squares) for 0.3-μm filament. Solid symbols are same quantities for 0.6-μm filament.

Using the Monte Carlo simulations and steepest-descent method, we have obtained the lowest free energy for a bundle with given length L and distance d between the two filament bases. The resulting critical distance for a given filament length is shown as the squares in Fig. 4 a. As we expected, the critical distances increase with the filament length, and the increase is somewhat superlinear.

FIGURE 4.

(a) Critical distances and (b) corrected critical distances as a function of filament length from energetics (squares) and dynamics (circles). The cutoff time for the dynamic simulations is 10 s. Open symbols are for E₀ = −15 k_BT and solid symbols are for E₀ = −7.5 k_BT.

In the dynamics simulations, we have calculated a time-dependent bundling probability by using a fixed ending time of 10 s. If the probability is larger than 50%, we consider the bundle to be formed within this time. Then we have a dynamic critical distance for a given filament length, which is indicated by the circles in Fig. 4 a. It is below the energetics line since the latter corresponds to the dynamics at infinite time. The shape of the dynamics line is similar to that of the energetics line, and the two are very close for d ≤ 0.6 μm. Thus for times greater than 10 s, energetics, rather than kinetic constraints, determines whether or not bundling occurs.

We have checked the errors in E_bend resulting from our approximations, by comparing the normal-mode model to a bead-spring model having the same filament profile. We find that E_bend is overestimated by 10–20% for most values of d < d_c. At d_c, E_bend is 40% overestimated for L = 0.6 μm and 60% overestimated for L = 1.0 μm. Since E_bend ∝ d², the fractional error in d_c is roughly half of that in E_bend, i.e., the E_bend error causes an ∼20% underestimate in d_c for L = 0.6 μm and a 30% underestimate for L = 1.0 μm. The main reason for the overestimate of E_bend is that our method ignores nonlinear corrections to Eq. 15. We have evaluated an approximation to these corrections using a simple continuum elasticity model for two filaments with parallel tips. The formula for E_bend in this model corresponding to Eq. 15 is whose minimum value is E_bend = (3l_p d²/2L³)k_BT (see Appendix). The exact result is 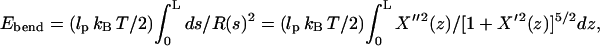since 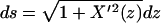and 1/R(s)² = X″²(z)/[1 + X′²(z)]³. We expand 1/[(1 + X′²(z))^5/2] for small X′ and keep the first term containing X′(z). This gives E_bend = (1 – 9d²/28L²)(3l_pd²/2L³)k_BT, so the fractional correction is 9d²/28L². We have compared this correction with the error of the normal-mode model relative to the bead-spring model and find they are close enough that the maximum difference in the bending energy is ∼10%. We use this result to correct the critical distance as follows: 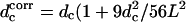). The corrected critical distance is shown in Fig. 4 b. The correction does not qualitatively change our results.

Fig. 5 shows snapshots of a dynamic simulation around the critical distance with E₀ = −7.5 k_BT (see Supplementary Material for videos). Before a stable bundle forms, two filaments will collide several times and form a metastable bundle, which may dissociate. When enough cross-linkers are added between the filaments and the filaments reach a profile with low bending energy, a stable bundle is formed. For long filaments (Fig. 5 a), several cross-linking points are required for a stable bundle; for short filaments (Fig. 5 b), two crosslinking points are sufficient. As Fig. 5 b shows, the first contact (or cross-linker attachment) usually occurs at the tips of the filaments, and resembles the Λ-precursors observed in experiments (47). Then the second contact occurs, and the filaments zip up as progressively more cross-linking proteins bind.

FIGURE 5.

Snapshots of filament profiles for (a) E₀ = −7.5 k_BT, L = 0.9 μm, and d = 0.45 μm; and (b) E₀ = −7.5 k_BT, L = 0.3 μm, and d = 0.125 μm.

DISCUSSION

The calculations above (Fig. 3) have shown that, except for a narrow range of distances and filament lengths, bundling times are well within the range of typical experimental timescales. The calculated bundling times are obviously dependent on our choice of the diffusion coefficient for actin and would increase by roughly a factor of 10 if we used the in vivo value for D; this would, however, still be within the experimental bounds. Thus filament cross-linking from a network is a viable route for formation of actin bundles. If one could establish how actin-binding proteins control the filament length and distance, one could connect the bundling time with the concentrations of these proteins and also obtain a phase diagram for bundling in terms of these proteins. The concentrations of capping protein, Arp2/3 complex, fascin or other cross-linking proteins, and actin itself, can affect the filament length and distance between filaments. Capping protein will reduce the filament length L if the actin concentration is fixed (4,50,51); intuitively, one would expect that L ∝ 1/k_cap, where k_cap is the capping rate. Increasing the actin concentration will increase the filament length, and it will also reduce the branch spacing because the branching rate increases (52). Arp2/3 complex can affect both the interfilament distance and the filament length. It enhances branching, which decreases the filament distance. On the other hand, it decreases the free-actin concentration by stimulating polymerization, which shortens the filament length (53,54). If such relationships could be made quantitative, we could obtain the bundling time versus capping protein concentration and Arp2/3 complex concentration, and the critical Arp2/3 complex concentration for bundling versus capping protein concentration.

At present, such quantitative relationships are not available, but we can make some qualitative observations. If we fix the Arp2/3 complex protein concentration, the bundling time will increase with decreasing actin concentration and increasing capping protein concentration because of their effects on filament length and branch spacing. When d ≪ d_c, the bundling time will vary smoothly since L and d are far from their critical values. When d ∼ d_c, the increase will be more abrupt because of the sharp dependence on d seen in Fig. 3. The concentration of fascin or other cross-linking proteins will also affect the bundling time and critical distance for a given filament length. Larger concentration or stronger interactions will enhance bundling and give a larger critical distance for a given filament length, until the crosslinking protein reaches saturation. Given all these considerations, we would expect a phase diagram qualitatively similar to that given in Fig. 6. All of the predictions outlined above are experimentally testable.

FIGURE 6.

Schematic of the phase diagram of network versus bundled structures in terms of fascin and capping protein concentrations.

Fig. 4 shows that the critical distances obtained from equilibrium energetics and dynamics are reasonably close for short filaments. This suggests that our cutoff time 10 s is greater than the characteristic bundling time for the range of L and d considered here. The close agreement of the equilibrium and dynamics results is important, since it implies that future calculations of bundling using more detailed filament models and interaction potentials can be performed using equilibrium total-energy calculations, which are faster than dynamic simulations. For longer filaments, the difference between the equilibrium and dynamics results grows with increasing d. We also see that the filaments can bundle with d/L ∼1 even though L ≪ l_p. Although one would expect such behavior for flexible filaments, it is somewhat counterintuitive in the semiflexible case, such as we have here. In addition, the strong binding from the fascin creates forces much stronger than the thermal forces. The value of d_c/L increases with increasing L, in agreement with elasticity-theory-based calculations (see Appendix).

Fig. 4 also shows that both the energetics and dynamics curves are fairly straight for short filaments. The upwards curvature seen for longer filaments is greater in the equilibrium calculations. In our simulation results, we find that the curvature is connected to the number of fascins attached, with greater curvature corresponding to more attached fascins. The bundle shown in Fig. 5 a has five fascins attached, and the filament tips are parallel to each other. The bundle in Fig. 5 b has only two fascins attached, and the filament tips are not parallel. For bundling geometries of this second type, the angle between two filaments is almost constant. As the spacing between the two fascins is 13 × 27 Å = 351 Å, and the center-to-center distance between two filaments where fascins attach is 155 Å, we determine this angle to be ∼52°. The two types of profiles shown in Fig. 5 have very different bending energies. Simple elastic calculations (see Appendix) predict that the dependence of the critical distance on length is linear for only two fascins attached as in Fig. 5 b (filaments tips not parallel), and curved upwards if there are more than two fascins attached as in Fig. 5 a (filaments tips parallel). This prediction is consistent with our energetics and dynamics results. For d = d_c with E₀ = −15 k_BT, there are only two fascins attached in all dynamics simulations, and in the equilibrium simulations for L ≤ 0.7 μm; for L > 0.7 μm, more than two fascins are attached. For both the energetics and dynamics simulations with E₀ = −7.5 k_BT, there are only two fascins if L ≤ 0.5 μm and more than two fascins if L > 0.5 μm. For d < d_c, the number of fascins required for a stable bundle is generally less than that required at d_c; for very small distances, the required number may be one. The number of fascins increases with increasing d for a given filament length L.

So far we have only discussed bundles formed by two filaments with parallel bases. From electron microscopy data it appears that filaments usually come from different mother-filaments, although it is possible that the daughter-filament and mother-filament at a branch point could form a bundle. An elasticity-theory-based calculation (see Appendix) shows that the total free energy of bundling is 4 tan²(70°/2)l_pk_BT/L_f + E_cross-link – TΔS, where L_f is the free filament length (see Fig. 7). This gives critical filament lengths for bundling of ∼0.4 μm for E₀ = −15 k_BT and 0.6 μm for E₀ = −7.5 k_BT. Thus if the spacing between two adjacent branching filaments exceeds 0.4–0.6 μm, the daughter filament and mother filament can form a bundle (see Fig. 7). Considering that the width of the lamellipodium is 1–2 μm, this suggests that mother-daughter filament bundling could act as a source of bundle nucleation. Further, for filament networks that contain long filaments and have a large spacing between branches, bundling from branch points may be important compared to other avenues.

FIGURE 7.

Schematic of bundling from an Arp2/3 complex branch point where the angle between the mother filament and daughter filament is 70°. The value L_b is the length of the cross-linked parts of the filaments; L_f is the length of the free parts of filaments. L = L_b + L_f is the total filament length, and X is the horizontal displacement of the filament at position z.

In our treatment of the nucleation phase of bundle formation, we have assumed that the critical nucleus consists of a pair of filaments. It is likely that once a stable two-filament bundle forms, other filaments will quickly form stable attachments to this bundle, because the added filaments can have favorable interactions with both of the bundled filaments. But it is possible that the critical nucleus consists of three or more filaments, and that this nucleus can form for L- and d-values where a two-filament nucleus is unstable. For E₀ = −15 k_BT, this is unlikely, because the bundling time is close to the first contact time, and two-filament contacts will occur before three-filament contacts. However, for E₀ = −7.5 k_BT, the possibility of a higher-order critical nucleus must be considered. The effect of this would be to place d_c somewhere between the values for E₀ = −7.5 k_BT and E₀ = −15 k_BT.

In summary, our simulations of constrained actin filament dynamics have shown that spontaneous cross-linking from a network geometry is a plausible route to bundle formation. Our results are compatible with existing experimental data and make predictions that could be tested by in vitro studies of bundling as a function of actin filament length and/or spacing. The key challenge in performing such studies would be precise control of the length and geometry of the actin filaments, which may be aided by the incorporation of new techniques from the nanoscience community.

APPENDIX

Dynamics equation

To obtain the dynamics equation for we first ignore the random thermal force and the cross-linking force in Eq. 2. Substitution of Eq. 3 into Eq. 2 gives

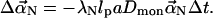(A1)

Since the elastic restoring force is proportional to 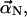we can regard each mode as a particle in an harmonic potential well. We rewrite Eq. A1 in the form 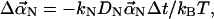where k_N is a spring constant, and D_N is the diffusion constant. Noting that the bending energy for each mode is

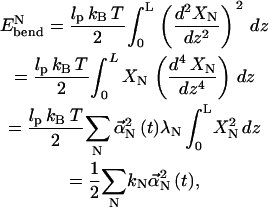we obtain 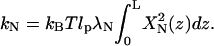Comparing the two different forms of the dynamics equation for each mode, we obtain 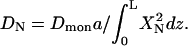If the cross-linking force in the x direction at position z is f(z), then cross-linking force on each mode in this direction is Since 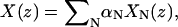the force on each mode along X direction is f_N = f(z)X_N(z). The y forces are treated in the same way. If there is more than one cross-linking site, the force on each mode is 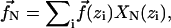where z_i is the position of the i^th cross-linking site. Combining all these terms gives the deterministic part of Eq. 6.

Entropy of bundling

We denote the entropy difference between free and bundled states ΔS. Since the filament tips have the same height (in our approximation) before and after bundling, ΔS = k_B ln(A₂/A₁) where A₁ and A₂ are the available areas of motion for the filament tips before and after bundling. After bundling, the main motion of each filament is around the fascin. The size of fascin is ∼165 Å × 72 Å × 117 Å (PDB 1DFC), and the difference between the cutoff distance of the cross-linking potential and the contact distance of the cross-linking potential is ∼25 Å. If the bundle is formed, the average thermal displacement of each filament should be much less than the potential width of 25 Å. We thus use 10 Å as the average thermal displacement of each filament. So the area of motion for each filament tip after bundling is ∼π × (10²/2) Ų. 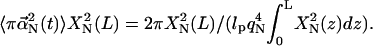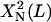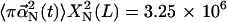The area of motion for each filament tip before bundling is approximately the same as the average area of motion of the first normal mode, We note that is independent of L and is proportional to L³; furthermore, our calculations show that Ų for length 1 μm. We thus have ΔS = [ln((π × 10²/2)/(2π × 3.25 × 10⁶)) – 3 ln(L/1μm)]k_B = −[13.2 + 3 ln(L/1 μm)]k_B, for any length L.

Elasticity-based calculation of bending energy

The bending energy for a filament with persistence length l_p and length L is if X(z) is not too large. Energy minimization to obtain the equilibrium filament profile followed by a straightforward integration by parts gives d⁴X/dz⁴ = 0. So the filament profile with the lowest bending energy will have the form X = c₀ + c₁z + c₂z² + c₃z³.

• Case 1. For a filament with its base fixed to be perpendicular to the substrate and the other end displaced by d/2 (half the distance to the other filament), the boundary conditions are: X(0) = 0, X′(0) = 0, X(L) = d/2. These imply that c₀ = c₁ = 0 and c₃ = (d/2)/L³ – c₂/L. Then the bending energy is 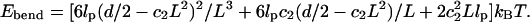From dE_bend/dc₂ = 0, we have the lowest bending energy: E_bend = (3l_pd²/8L³)k_BT.

• Case 2. If both of the filament's ends are fixed to be perpendicular to the (x,y) plane (similar to Fig. 5 a), and have relative displacement d/2, the boundary conditions X(0) = 0, X′(0) = 0, X(L) = d/2 and X′(L) = 0, give E_bend = (3l_pd²/2L³)k_BT.

• Case 3. If a filament's base is fixed to be perpendicular to the substrate and the other end has an angle β relative to the vertical, the boundary conditions are: X(0) = 0, X′(0) = 0, X(L) = d/2, X′(L) = tan β. Then E_bend = (3l_pd²/2L³ – 3l_pd tan β/L² + 2l_p tan² β/L)k_BT.

For a given filament length, we can calculate the critical distance d_c, which gives zero bundling free energy, for different types of bundling profiles (see Fig. 5). The bundling free energy is E_bend + E_cross-link – TΔS, where E_cross-link = nE₀, n is the number of cross-linkers, and E₀ is the binding energy per fascin. We obtain the dependence of d_c on L by taking E_cross-link and ΔS to be independent of L, since E_crosslink is determined mainly by the tip geometry and ΔS depends only weakly on L. Because ΔF_tot = 0 at the transition, this is equivalent to keeping E_bend fixed in calculating the L-dependence of d_c. If there is only one cross-linker, the filament tip's orientation has no constraints. Then we can calculate the bending energy using Case 1. If there are two cross-linkers, so that the angle between the two filaments is constant, we calculate the bending energy using Case 3. We cannot obtain a simple analytic solution for d_c in terms of L in this case, but a simple numerical solution gives a dependence that is close to linear in L. If there are more than two cross-linkers, the two filament tips are parallel to each other, and we use Case 2. In this case, d_c ∝ L^3/2.

Bundling from branch points

For bundling from branch points (Fig. 7), the boundary conditions are X(0) = 0, X′(0) = tan(70°/2), X(L_f) = 0, and X′(L_f) = 0, where L_f is the free filament length. From these boundary conditions we can obtain the value of the coefficients c₀ – c₃ above, and then E_bend. The value E_bend for each filament is 2 tan²(70°/2)l_pk_BT/L_f (from Case 3 above). Then the total free energy difference is ΔF_tot = 4 tan²(70°/2)l_pk_BT/L_f + E_cross-link – TΔS. The critical filament length L_c makes ΔF_tot = 0. We obtain L_c for each value of n and choose the n that gives the smallest L_c. For E₀ = −7.5 k_BT, 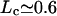μm, and for E₀ = −15 k_BT, 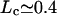μm.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.