Figure 4.

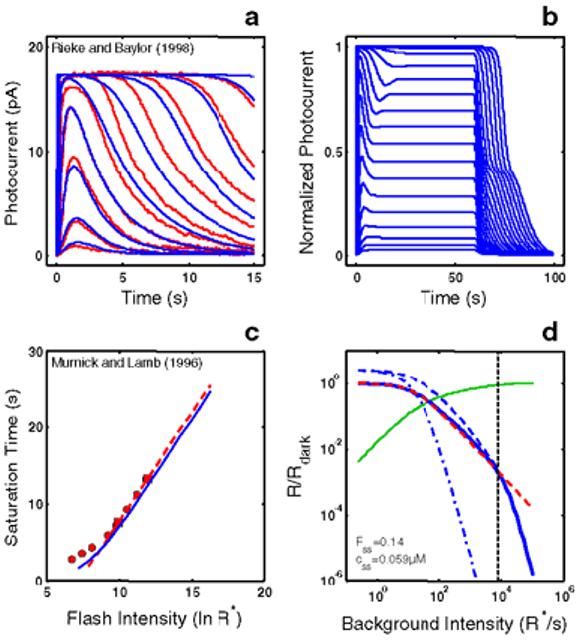
RecRK model accounts for Empirical Response Suite I with τ_E rate-limiting. A : The RecRK model (with τ_E rate-limiting) was optimized to both the Murnick & Lamb saturated two-flash data and to four sub-saturating flash responses from toad rods (four smallest responses). The model is able to provide a reasonable account of the 4 sub-saturating responses as well as responses to 5 higher intensities (to which the model was not optimized). B : Model step responses reproduce the “nose” at step onset and the two-phase response at step offset. C : The model T_sat versus ln(I) function (blue solid curve) reproduces the same slope as the Murnick & Lamb data (∼2.8 s/ln unit; red data and dashed line as in Figure 1B). Finally, the model generates a substantial range of Weber's law LA flash sensitivity (∼3 log units; solid blue curve, panel D ). For each of a series of background adaptation levels (I_b), model LA flash sensitivity was defined as the amplitude of the response to a flash of fixed criterion intensity divided by the intensity of the criterion flash. The criterion was the flash intensity eliciting a DA flash response amplitude that was 10% of the full range of circulating current. The dashed red curve is the Weber-Fechner relation from Figure 1D, shifted horizontally to fit the model output below a “cutoff” background intensity (cutoff I_b), marked by a dotted vertical cursor, above which the model was judged to deviate from Weber's law. The cutoff I_b was defined as the highest I_b at which the value of the model deviated from the best-fit Weber-Fechner curve by a criterion amount (0.05 log units). The Weber-Fechner curve was fit (least-squares) to the model over all I_b values up to and including the highest I_b where the model slope was still >= −1. The model slope was estimated by fitting a line to a moving window of 3 adjacent model points (sampling every 2^0.25 R*/s, or 0.075 log units). Note that the model LA flash sensitivity obeys Weber's law over a significant range (cutoff I_b = 8000 R* s⁻¹. At the cutoff I_b, 14% of the model DA circulating current (F_ss) remains, as indicated by the intersection of the vertical cursor line with the green solid curve. The latter plots the fraction that the steady-state current is saturated (i.e., 1 - F_ss(I_b)), where F_ssis the steady-state circulating current defined to be 1.0 in the dark, and zero when all channels are closed. Also, at the cutoff I_b, the steady-state internal Ca⁺⁺level (c_ss in inset) has dropped by a factor of 5.1, from a dark value of 0.3 μM to 0.059 μM. Also shown is the LA flash sensitivity of the model under two types of simulated Ca⁺⁺ clamp conditions: (1) LA flash sensitivity with Ca⁺⁺ clamped at its dark value (Ca⁺⁺_dark clamp; blue dash-dot curve). Ca⁺⁺feedback is fully disabled over the entire dynamic range, with only static saturation contributing to flash desensitization. Ca⁺⁺ was fixed at its dark value in the model, and I_b was adjusted to achieve the same steady-state current as in the unclamped case, ensuring that the steady-state currents were at the same level in relation to static saturation (i.e., cGMP-gated channel). Differences in flash sensitivity then can be ascribed to the differing states of Ca⁺⁺ in the unclamped and clamped cases. The Ca⁺⁺ clamp analysis equates steady-state current levels (F_ss), but does not equate internal Ca⁺⁺ levels at the time of presentation of the flash. This is achieved in a second analysis: (2) LA flash sensitivity with Ca⁺⁺ clamped at the new steady-state level reached in response to each I_b(Ca_ss⁺⁺ clamp; blue dashed curve). This approach equates the F_ss (and hence equates the effect of channel saturation), and equates Ca⁺⁺ at the time of the flash. Thus, in comparing the unclamped and the Ca_ss⁺⁺-clamped flash sensitivity, the LA flash response in each case is affected equally by saturation and by the steady-state level of Ca⁺⁺-mediated gain. The only additional factor shaping the LA flash response in the unclamped case is the dynamic Ca⁺⁺-mediated gain change evoked by the flash. Note that at high I_b (I_b> cutoff I_b), the unclamped model flash sensitivity falls more steeply than a Weber's law slope of −1, and eventually follows a steep function that parallels the high - I_b behavior of both Ca⁺⁺ clamped curves. In fact, all 3 curves asymptote to a slope of -(n_cg + 1), which is predicted by the instantaneous compressive saturation of the cGMP-gated channels [30].