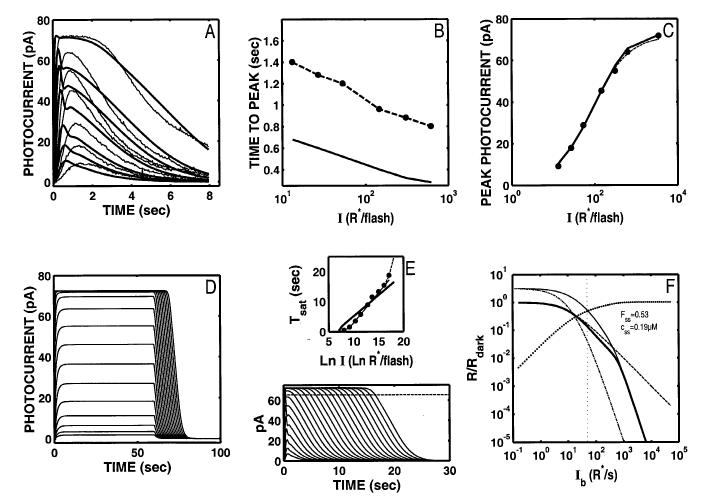
Fig. 2.

The S/R suite is shown for the Nikonov et al. (1998) model using the parameter values that fit the dim-flash response from their rod a (control response in Ringer’s). Parameters are given in Table 2. Model output is shown as solid lines and curves. Data from Fig. 1 are shown by data points and dashed lines and curves. (A) The fit to the Ref data set is poor (relLSQerr = 0.0226), and neither the growth of T_pk nor R_pk with flash I (B,C) match the voltage-clamped Ref data. Note that the model generates an aberrant “nose” at the peak of the flash response (A). This feature is more pronounced at higher intensities. (D) The model step responses are missing the features at step onset and offset (compare with Fig. 1D). (E) The slope of the T_sat function is shallower than the most frequently reported slope (2 s/ln unit). (F) Model LA flash sensitivity (thick, solid curve). The model LA flash sensitivity was defined as the amplitude of the response to a flash of fixed (criterion) intensity in the presence of a background adaptation, divided by the amplitude of the criterion flash presented in the absence of a background. The criterion used was a flash eliciting a DA flash response amplitude that was 10% of the full range of circulating current. The dashed curve is the Weber-Fechner relation from Fig. 1 F, shifted horizontally to fit the model output below a “cutoff” I_b (indicated by the dotted vertical cursor), above which the model was judged to deviate from Weber’s law (see text for details). The I_1/2 for the Weber-Fechner curve is 9.85 R^* s^-1. With the Nikonov et al. dim-flash, suction electrode parameters, the model LA flash sensitivity does not obey Weber’s law over any significant range (cutoff I_b = ∼49 R^* s^-1). At the cutoff I_b, 53% of the model DA circulating current remains, as indicated by the intersection of the vertical cursor line with a curve plotting the fraction that the steady-state current that is saturated (i.e. 1 - F_ss(I_b), shown as solid dots). Here, F_ss is the steady-state circulating current defined to be 1.0 in the dark, and zero when all channels are closed. Also, at the cutoff I_b, the steady-state internal Ca²⁺ level (c_ss in inset) has dropped by slightly more than a factor of 2, from a dark value of 0.385 μM to 0.19 μM. Also shown is the LA flash sensitivity of the model under two types of simulated Ca²⁺-clamp conditions: (1) L A flash sensitivity with Ca²⁺ clamped at its dark value (${\mathrm{Ca}}_{dark}^{2+}$-clamp; dash-dot curve). Ca²⁺ feedback is fully disabled over the entire dynamic range, with only static saturation contributing to flash desensitization. Ca²⁺ was fixed at its dark value in the model, and I_b was adjusted to achieve the same steady-state current (F_ss) responses as in the unclamped case, ensuring that the steady-state currents were placed at the same level in relation to static saturation (i.e. cGMP-gated channel). Differences in flash sensitivity then can be ascribed to the differing states of Ca²⁺ in the unclamped and clamped cases. The ${\mathrm{Ca}}_{dark}^{2+}$-clamp analysis equated steady-state current levels (F_ss), but did not equate internal Ca²⁺ levels at the time of presentation of the flash. This was achieved in the second analysis: (2) L A flash sensitivity with Ca²⁺ clamped at the new steady-state level reached in response to each I_b (${\mathrm{Ca}}_{SS}^{2+}$ clamp; thin solid curve). This approach equated the F_ss (and hence equated the effect of channel saturation), and equated Ca²⁺ at the time of the flash. Thus, in comparing the unclamped and the ${\mathrm{Ca}}_{SS}^{2+}$-clamped flash sensitivity, the flash response is affected equally by saturation and by the steady-state level of Ca²⁺-mediated gain. The only additional factor shaping the LA flash response in the unclamped case is the dynamic Ca²⁺-mediated gain evoked by the flash. Note that at high I_b (I_b > cutoff I_b), the unclamped model flash sensitivity falls more steeply than a Weber’s law slope of -1, and eventually follows a steep function that parallels the high-I_b behavior of both Ca²⁺-clamped curves. In fact, all three curves asymptote to a slope of -(n_cg + 1), which is predicted by the instantaneous compressive saturation of the cGMP-gated channels (Matthews et al., 1990).