Generation of Focused Electric Field Patterns at Dielectric Surfaces

Abstract

We here report on a concept for creating well-defined electric field gradients between the boundaries of capillary electrode (a capillary of a nonconducting material equipped with an interior metal electrode) outlets, and dielectric surfaces. By keeping a capillary electrode opening close to a boundary between a conducting solution and a nonconducting medium, a high electric field can be created close to the interface by field focusing effects. By varying the inner and outer diameters of the capillary, the span of electric field strengths and the field gradient obtained can be controlled, and by varying the slit height between the capillary rim and the surface, or the applied current, the average field strength and gradient can be varied. Field focusing effects and generation of electric field patterns were analyzed using finite element method simulations. We experimentally verified the method by electroporation of a fluorescent dye (fluorescein diphosphate) into adherent, monolayered cells (PC-12 and WSS-1) and obtained a pattern of fluorescent cells corresponding to the focused electric field.

Electromanipulation, i.e., the use of electric fields to manipulate or affect materials or objects, are used in several areas. Examples include breakdown of dielectrics,^1,2 molecular rearrangement,³ electric trapping,^4–6 induction of electron transfer,⁷ electrophoresis,⁸ dielectrophoresis,^9,10 and different forms of surface patterning.¹¹

In many applications, a spatially selective exposure is desired, and electric fields that are highly localized compared to the working length scale must be used. Such fields can be created by the use of electrodes that are small compared to the working length scale¹² or by the use of materials of different conductivities to focus an electric field. In the areas of analytical chemistry and biotechnology, electrolyte-filled capillaries,¹³ glass pipets (patch-clamp pipets),^14,15 and microfabricated channels/orifices¹⁶ have previously been used for electromanipulation of biological materials, such as tissues, cells, and organelles.

Here, we present a new, simple method to create focused electric field gradients and patterns at dielectric surfaces, i.e., at interfaces between a conducting solution and a nonconducting medium, such as glass, polystyrene plates, or a nonconducting fluid. We demonstrate the method by using homemade plastic capillary electrodes consisting of a capillary equipped with an interior metal electrode. By positioning the outlet of the capillary near a glass surface in the conducting solution, and by applying an electric current between the inside metal electrode and an outside ground electrode, local electric field intensification is created under the rim of the capillary. The narrow slit between the capillary rim and the surface forces the current and field lines to converge when passing out to the bulk volume, and a local, focused field pattern is obtained. The extension of the focused field, the field strength, and the gradient of the field can be chosen by changing the capillary inner diameter (i.d.) and outer diameter (o.d.), slit height or average current density. The appearance of the field was simulated with the finite element method (FEM) program Femlab (Comsol, Stockholm, Sweden). The simulations are scalable and can be used for dimensions of cylindrical structures other than the capillary electrodes used here. Previously, the electric field outside capillary electrode outlets has been approximated with the analytical solution for a field outside a conducting disk in an isolated plane.¹³ This model does not account for the presence of proximal dielectric surfaces. However, such surfaces are often present in experimental work with, for example, biological cells and other materials, and changes the field appearance qualitatively. Knowledge of the distribution of the electric field outside capillary electrodes is valuable in applications where it is actively utilized but also when it can interfere with processes. Examples are electric potential induction in electrochemical detection of solutes¹⁷ or when using biological units such as cells for detection, at electrolyte-filled capillary endings.¹⁸

To experimentally verify the generation of electric field patterns, we used monolayered cells as biosensors and performed spatially selective electroporation. A fluorescent dye and a local electric field pattern were delivered to the cells via the capillary electrode, and a corresponding pattern of electromanipulated cells having internalized the dye was created in the monolayer. When exposing a cell to an electric field, a membrane potential being proportional to the electric field strength is induced.¹⁹ To obtain electroporation, i.e., pore formation in the cell membrane, the induced potential must reach a critical threshold value.²⁰ On the other hand, the induced potential must not be too large, as the pore formation then becomes irreversible and causes cell death.²¹ Further, the induced transmembrane voltage induced at certain field strengths depends on both cell shape and cell size.²⁰ To make sure that cells are electroporated but not killed, methods to measure pore formation during electroporation have been proposed.^16,22 Using the herein proposed setup with the inherent electric field gradients, such controls are not needed. Due to the electric field gradient, the system is less sensitive to variations in the cell population or between cell batches, as well as to deviations in the positioning of the capillary. Cells at some distance from the center of the capillary will experience the optimal field and be successfully electroporated.

MATERIALS AND METHODS

Finite Element Method Simulations

To elucidate the electric field at capillary electrode outlets and the field focusing obtained upon lowering a capillary electrode close to a dielectric surface, we performed FEM simulations with the commercial finite element method program Femlab. The simulations were performed for two different capillary electrodes (i.d. = 400 μm, o.d. = 800 μm and i.d. = 400 μm, o.d. = 3000 μm) and for two different slit heights (s = 400 μm and s = 50 μm). To make the simulations less memory demanding, only one-quarter of the lower end of the capillary electrode and the cell bath was simulated. An illustrative example of a modeling geometry is shown in Figure 2C. Besides capillary dimensions and slit heights, the only difference between simulations was that a larger bath (r_bath = 3000 μm instead of r_bath = 2000 μm) was used for the thick-walled capillary.

Figure 2.

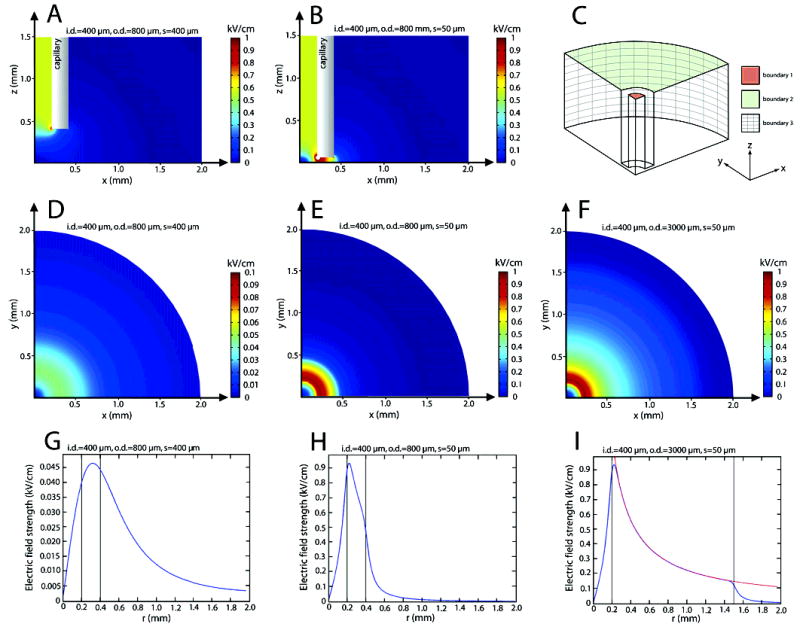
FEM simulations of the distribution of electric field under the rim of the capillary electrode. (A) and (B) show cross sections of a capillary electrode (i.d. = 400 μm, o.d. = 800 μm) kept 400 (A) and 50 μm (B) above a nonconducting surface. In (C), the geometry used for a FEM simulation of the electric field is shown. To make the simulations less memory demanding, symmetry was utilized and only one-quarter of the lower end of the capillary and its surrounding simulated. (D)-(F) show the electric field 3 μm above the bottom surface (z = 3 μm) for the following capillary electrodes: (D) i.d. = 400 μm, o.d. = 800 μm, and slit height s = 400 μm; (E) i.d. = 400 μm, o.d. = 800 μm, and slit height s = 50 μm; (F) i.d. = 400 μm, o.d. = 3000 μm, and slit height s = 50 μm. Note that the scale in (D) is different from the scales in (E) and (F). (G–I) Plots of how the electric field strength varies with r (r = (x² + y²)^1/2) for three different capillary electrodes: (G) i.d. = 400 μm, o.d. = 800 μm, and slit height s = 400 μm; (H) i.d. = 400 μm, o.d. = 800 μm, slit height s = 50 μm; (I) i.d. = 400 μm, o.d. = 3000 μm, slit height s = 50 μm. Note that (G) has a different scale than (H) and (I). The black lines mark the inner and outer diameters of the capillary electrodes. As can be seen, the field declines fast outside a capillary electrode when its rim is held close to the bottom surface. Note the similarity in the field distribution for r < 400 μm in (H) and (I). Assuming no current flow in the z direction under the rim of a capillary, the total current passing at any height above the surface is constant for all radii. Thus, |E|·r = K, where K is a constant that can be decided by any valid combination of E and r. This also implies that the electric field should decrease proportional to K/r as r is increased. By readout from (I), K could be decided to 0.91 for the used settings. The red line in (I) is the curve |E| = 0.91/r, and as can be seen, it follows the simulated field profile almost perfect under the rim of the capillary.

The equation ∇·(σ ∇V) = 0, where σ is the conductivity and V the potential was solved. The conductivity was set to 3.5 mS/cm. At boundary 1 (see Figure 2C), the inward current density normal to the boundary surface, was set to 20 000 A/m² (−n·J = J_n, where n is the normal to the boundary, J the current density and J_n the normal component of the current density). This corresponds to a total current of 2.5 mA flowing through the capillary electrode. On boundaries 2 and 3 (see Figure 2C) the potential was set to zero (V = 0). On all other boundaries, electric insulation/symmetry (−n·J = 0) was used. The simulations are valid under the assumption that the conductivity is constant and that current contributions due to buildup of ion concentration gradients are negligible.

Electroporation

Adherent PC-12 cells and WSS-1 cells were grown for 2–3 days on glass-bottomed cell dishes (WillCo Wells BV, The Netherlands) according to standard procedures, at 37 °C in a humidified 5% CO₂, 95% air atmosphere. Prior to experiment, culture medium was replaced by a low-conductivity electroporation buffer. Cell dishes were transferred to an inverted microscope (Leica DMIRB, Wetzlar, Germany).

The capillary electrodes, 15–20 mm long, were either composed of the cut lower parts of ordinary polypropylene micropipet tips or of homemade cylinders of Delrin modified with an internal electrode (2–3 mm of thin platinum wire) positioned at the capillary inlet. The capillary electrode was filled with 100 μM fluorescein diphosphate diluted in low-conductivity buffer. The cell bathing medium was grounded with a platinum wire positioned ~1 cm from the capillary electrode.

The capillary electrode was vertically positioned at a height of 50 μm above the bottom of the cell dish with a high-graduation micromanipulator (Narishige, MWH-3, Tokyo, Japan). Electroporation was performed by applying 30 sequential 100-ms current square pulses with maximum amplitude of 2.5–3 mA and 100 ms resting time between, using a dc high-voltage power supply (model ECM 830, BTX, Holliston, MA). Pulsing was thus performed during a total time period of 6 s. We chose to apply current pulses instead of voltage pulses as the electric field in the slit region is decided by the local resistance and the current density. Applying voltage pulses is equally plausible, assuming that the total resistance of the system is known. The resistances between the metal electrode inside the capillary and the outside ground electrode were in these setups 60–70 kΩ, which means that the applied voltages were 150–210 V. The experimental setup is shown in Figure 1. To remove excess uncaptured dye after electroporation experiments, cells were washed with fresh electroporation buffer before images were recorded. All experiments were performed at room temperature. Readout was performed after the experiment using conventional fluorescence microscopy (Leica I3 filter cube, 10× or 5× objectives). Images were recorded using a digital CCD camera (Hamamatsu, Kista, Sweden). Control experiments were performed by exposing cells to a continuous 10 μL/min flow of FDP-containing electrolyte for 30 s, having the capillary electrode positioned and loaded as described above, but without applying any current.

Figure 1.

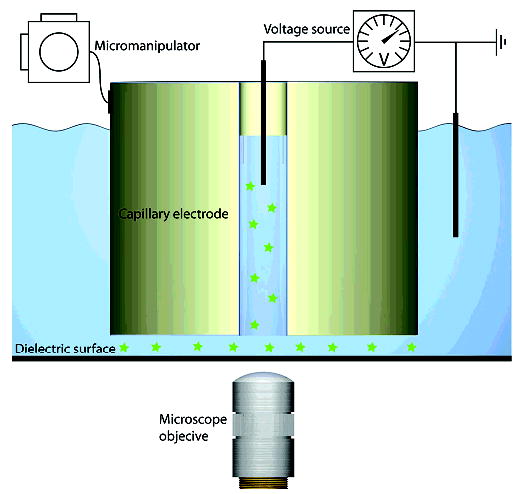
Schematic of the setup used for focused field pattern generation. A capillary electrode is filled with conducting medium and positioned close to the dielectric surface by using a micromanipulator. A current is applied over the electrode inside the capillary and a ground electrode placed in the bath. An electric field will then be obtained inside and outside the capillary electrode. If the distance between the rim of the capillary and the dielectric bottom of the cell bath is small enough, the electric field will be intensified under the rim. As the electric field is applied, compounds in the electrolyte are fed to the slit volume through electrophoresis.

Chemicals

Fluorescein Diphosphate (FDP) was purchased from Molecular Probes (Leiden, The Netherlands). Low-conductivity (3.5 mS/cm at 25 °C) isoosmolar electroporation buffer was purchased from Eppendorf AG (Hamburg, Germany).

RESULT AND DISCUSSION

The experimental setup for generation of focused electric fields at dielectric surfaces is schematically described in Figure 1. The capillary electrode is positioned near a glass surface at a distance of 50–400 μm, using a micromanipulator. Agent-containing solutions can be delivered through the capillary electrode, either by electrophoresis or by pressure-driven flow, and the electric field patterns are generated when current is applied.

Simulations

Figure 2A shows a FEM simulation of the created electric field for a capillary electrode of the following dimensions: i.d. 400 μm and o.d. 800 μm, positioned 400 μm above a nonconducting surface. As can be seen, the field is strongest inside the capillary and declines rapidly with distance from its opening. At this slit height, the focusing effect is very small. At the dielectric surface, a smoothly varying field, with a magnitude of only a fraction of the field inside the capillary electrode, is obtained (Figure 2D). The field, at the dielectric surface, becomes zero along the centerline axis of the capillary (bottom left corner, Figure 2D), has its maximum strength under the rim of the capillary, and declines slowly as the outer radius of it is passed. A circle-shaped pattern of focused electric field is thus generated. This should be compared with setups where no dielectric surface is present. In this instance, with the same distance from the orifice, the field instead has it maximum along the capillary centerline where, in our case, it is zero.^13,23

By lowering the capillary electrode closer to the surface, not only the magnitude of the field but also the distribution of the field is changed. This is the result from further forced focusing of field lines and current paths through the narrowed slit between the cut end of the capillary wall and the bottom surface. As the outer edge of the capillary is reached, the current is again allowed to spread in three dimensions and the field declines abruptly. Panels B, E, and H in Figure 2 show the electric field distribution obtained when the capillary orifice is lowered to a distance of 50 μm above the surface. Besides higher field strengths, a smaller slit height also gives a field that increases and declines in a more distinct manner, as is illustrated in Figure 2D,E and Figure 2G,H.

If higher or lower field strengths are desired, the applied current or slit height is just changed correspondingly. The simulations are valid under the assumptions that the conductivity is unchanged and constant within the bulk solution and that current contributions due to buildup of ion concentration gradients are negligible. As long as this applies, the simulations are scalable to hold for different applied currents as well as different dimensions. A change in applied current by a factor x, changes the electric field strengths given in the figures by the same factor. Note that Joule heating is always present to some degree in this type of system, which for sufficiently high and long current pulses alters the local conductivity and thus the electric field distribution. This is not further discussed in this note as the degree of conductivity change depends on details of the chosen experimental conditions, such as the length of the current pulse, the heat capacitivities of present solutions/materials, the efficiency of thermal diffusion in the setup, and the temperature-conductivity relation for the conductive solution.

By varying the wall thickness of the capillary electrode, the surface area experiencing increased field strength can be controlled. In Figure 2F and I, simulations of a thick-walled capillary electrode are shown. The i.d. is the same as in (D) and (E), but the o.d. is set to 3000 μm instead of 800 μm. The slit height is the same as in Figure 2E, i.e., 50 μm. Neglecting edge effects, the electric field strength in the slit decreases proportionally to 1/r as the radius increases. This can be understood by noticing that there is no flow of current in the z direction, which shows that the product of the magnitude of the electric field E and the radius r, must be constant for reasons of geometry. That this holds close to the surface is shown by the red curve (1/r), in Figure 2I. Knowing the simple relation governing the decline of the field under the rim of the capillary, the inner and outer diameters can be chosen to give a desired span of field strengths merely by studying a 1/r curve. For example, if the desired electric field should be two times higher for a radius corresponding to the inner rim of the pipet than at the outer rim (i.e., E_i/E_o = 2), a capillary electrode where the outer diameter is two times the inner diameter (i.e., r_o/r_i = 2) should be chosen. Further, a small inner diameter gives a steeper field decline, as seen in Figure 2I.

Electroporation Experiments

To experimentally evaluate the method of field focusing, we positioned a capillary electrode 50 μm above a nonconducting surface covered with adherent cells, cultured for 2–3 days. The experimental setup is shown in Figure 1, except for the monolayer of cells covering the surface. The capillary electrode was filled with a low-conducting electrolyte supplemented with a fluorescent dye, FDP. FDP is almost nonfluorescent until it is digested to fluorescein by phosphatases in the cytoplasm of cells.

To achieve electropohoretic delivery of FDP (with four negative charges) to the cells upon pulse application, the polarity of the pulses in the electroporation experiments were reversed compared to those used in the simulations. The electrophoretic velocity of a molecule v_ep is described by v_ep = μ_ep·E, where μ_ep is the electrophoretic mobility and E the electric field. The electrophoretic mobility μ_ep is given by μ_ep = q/6πηr_g, where q is the molecular charge, η the viscosity, and r_g the radius of gyration. For positively charged compounds, a polarity of the pulses as used in the simulations would give the right electrophoretic migration direction, and for uncharged substances, gravitation or pressure-driven flow can be used. Although electroosmosis contributes to the transport, it has a reduced importance, due to the dimensions of the capillary electrode and the short pulse duration.²⁴ Upon pulse application, pores are formed in cells experiencing the focused electric field, i.e. cells situated under the capillary wall, and FDP is internalized to the cytoplasm, Figure 3. The area of the focused electric field, and thus, the electroporated area, is decided by the wall thickness of the capillary electrode. This is clearly illustrated in Figure 3A and B, showing fluorescence micrographs of patterns of electroporated cells. The pictures are from two experiments being identical with the exception of a larger capillary outer diameter in B, compared to A (o.d. = 800 μm in A and o.d. = 3000 μm in B). In B, the electroporated area extends further than could be viewed with our microscope set up. Note that the areas of electroporated cells follows the dimensions of the capillaries as predicted by FEM simulations. The outlet of the capillary electrode used for the experiment in B is shown in Figure 3C.

Figure 3.

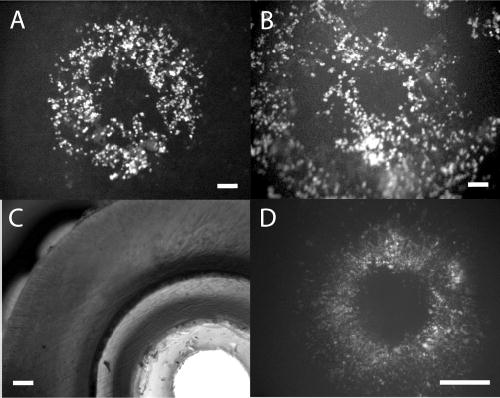
Electroporation of adherent cells by electric field focusing. (A) shows a fluorescence micrograph of monolayered PC-12 cells electroporated with fluorescein diphosphate by a capillary electrode of i.d. 400 μm and o.d. 800 μm. The ring shape occurs when the field lines converge under the capillary wall, leaving an area of low field strength at the centerline extension of the capillary. The scale bar is 100 μm. In (B) the o.d. was changed to 3000 μm. When the o.d. is increased, the area that experiences the focused field is extended, and a larger ring pattern of electroporated cells is obtained. Here the area of electroporated cells continues outside the figure, which was limited by the field of vision of the microscope. The scale bar is 100 μm. (C) The tip of the capillary electrode used in (B). The scale bar is 100 μm. (D) shows electroporation in a confluent layer of WSS-1 cells with a capillary electrode of i.d. 1000 μm and o.d. 2500 μm. In this experiment, a gradient in degree of electroporation, corresponding to the decline of field strength for increasing r, is clearly noticeable. The scale bar is 500 μm.

Increasing the inner diameter of the capillary yields a correspondingly larger nonelectroporated middle area, as shown in Figure 3D. In this experiment, WSS-1 cells are used, that are typically small, 5–10 μm in diameter, very extended, and grow very close together. As detectors of electric fields, they thus give a higher resolution compared to PC-12 cells, which are larger and grow less dense. So, in this experiment, it is clearly noticeable that we have a field gradient under the rim of the capillary. The fluorescence intensity is higher under the inner rim of the capillary, because more cells have become electroporated. Under the outer rim, fewer cells are electroporated, and fluorescence therefore seems weaker and more scattered.

The transfer of current from the platinum wires, serving as electrodes, to the solution takes place through electrochemical reactions at the electrode surfaces. These reactions produce gas as well as affect the ion concentration close to the electrodes and possibly, if ions are not found in excess, the ion concentration in the bulk solution. A large gas production might affect the electrical contact between the metal electrode and the solution, and a buildup of concentration gradients in the simulated region of the setup would result in diffusion-driven currents, which is not included in the simulations. These issues are not a concern for the present setup and the used experimental protocols, but should be considered if the total amount of current over time is increased much, if the ion concentration lowered, or if the bulk solution volume close to the electrodes is dramatically downscaled. However, as the appearance of the metal electrodes and the region close to them is not of other importance to the field focusing region, such a problem in the end concentrates to a mere design issue.

In the simulations, the grounding of the solution surrounding the capillary electrode was performed in an axisymmetrical manner, while in the experimental setup, it was accomplished with a platinum wire positioned some centimeters from the capillary. Due to the negligibly small voltage drop close to the ground electrode, the resulting deviations in field distribution in the simulated area are far smaller than the resolution in the simulations. This was verified in control simulations not included in the paper. That the exact position and features of the ground electrode are of minor importance is further indicated by the symmetrical appearance of the electroporated area. (see Figure 3).

CONCLUSIONS

We have described a simple method to produce well-defined, focused electric field patterns along nonconducting surfaces. The method was illustrated in the field of electroporation. The experimental results agreed well with field distributions predicted from FEM simulations. As proposed previously, when using hollow structures for electroporation, the cell-loading agents can be applied to the cells from inside the capillary electrode. Such local delivery is advantageous in reducing the amount of cell-loading agent.²⁵ This note has focused on creation of electric field patterns and was illustrated experimentally in the field of electroporation; however, we suggest using these principles of field intensification for other types of electromanipulation. Mounting the capillary electrode on, for example, a micromanipulator, it can be moved up and around either to stamp/electroporate distinct areas through switching on/off the electric field and moving the capillary electrode, or the capillary electrode can be used as a pencil for writing in a similar manner as in SPM surface patterning techniques.¹¹ Possible applications are dielectrophoretic trapping, electrophoretic extraction/ejection of molecules, and bleaching of fluorescence spots in microarray formats and surface modifications. Since the scaling of the length dimension in the equations describing the electric field distribution does not affect the field pattern, the simulations are scalable, and the concept applicable for larger, as well as smaller structures. Decreasing the dimension, the limit is set by practical issues such as fabrication and limits in positioning the structure sufficiently close to the surface. Further, the principle of field intensification in small spaces above nonconducting surfaces can be used for types of geometries other than hollow cylinders. For example, using a capillary divided in two half-moon formed channels by a separating wall, i.e., a so-called theta capillary, and applying a potential difference between the channels, a current will pass under the separating wall, and a corresponding string of an intensified field can be created. This is a suitable structure to use if field gradients within the high-field area are not desired.

For electroporation of cells, the inherent field gradients guarantee that some cells will be exposed to optimal conditions, which makes the method especially suitable for applications where a presearch for optimal pulse protocols is not possible.