Skip to main content
. Author manuscript; available in PMC: 2006 Jun 23.
Published in final edited form as: Curr Opin Struct Biol. 2005 Oct;15(5):586–592. doi: 10.1016/j.sbi.2005.08.007

Figure 1.

Figure 1

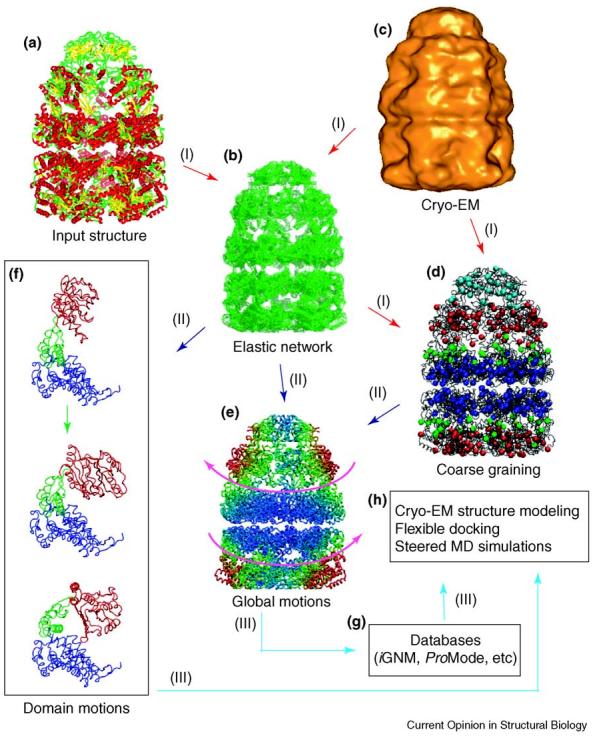
Overview of various methodologies and applications to the GroEL–GroES complex of EN models. The EN model (b) requires an initial input structure, typically an atomic-resolution structure such as in (a), colored according to secondary structure elements. As noted in the text, a lower-resolution structure, such as a cryo-EM map (c), can also be used as input for constructing an EN model. In order to process supramolecular assemblies, further coarse graining (d) is adopted. A low-resolution EN model in which only every 20th residue is used to define the nodes is shown. Once the EN model is constructed, various motions are calculable by NMA, ranging from the level of the entire molecule to domains and individual residues. (e) The global motions computed for the GroEL–GroES complex (PDB code 1gru) [68], revealing a counter-rotation of the GroES-bound (trans) ring with respect to the lower (cis) ring (as shown by the magenta arrows). The structure has been colored by increasing mobility from blue to red, showing that the mobility increases with increasing distance from the interface between the cis–trans rings and from the cylindrical axis of symmetry. (f) The motions of the individual subunits, each composed of three domains (apical, red; intermediate, green; equatorial, blue), obtained from analysis of the EN model. The top diagram shows the ATP-bound form of a subunit in the trans ring and the lowest diagram is its unliganded counterpart in the cis ring. Applying the deformations from the first (slowest) mode calculated by NMA to the trans ring monomer produces the middle structure, demonstrating the intrinsic (structure-encoded) ability of the subunit to reconfigure into the closed form assumed in the cis ring. This is consistent with successive interchange of the subunit conformations between the two forms upon binding of the cap to either ring and cap dissociation during the chaperonin cycle. From these calculations, (g) databases of global motions have been constructed, and (h) several important additional applications of these motions and deformations have been indicated.