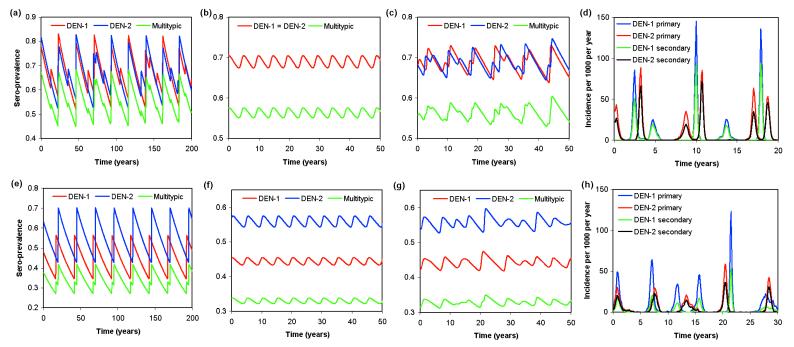
Figure 2.

(a–c) Sero-prevalence time series for system with R₀₁ = R₀₂ = 2, σ = 100/yr, 1/μ = 50 yr, φ₁ = φ₂ = 2.5. (a) Deterministic model, with λ₀ = 0. Note that the dynamics are chaotic with a quasi-period of about 25 yr. A symmetry-breaking bifurcation has given rise to partially nonsynchronized oscillations of the two strains. (b) Deterministic model with λ₀ = 10⁻⁶. The background force of infection eliminates large-amplitude limit cycle or chaotic attractors, simplifying the dynamics and restoring exact synchronization of the oscillations of both strains. (c) Stochastic model with λ₀ = 10⁻⁶. The dynamics show the “ghost” of the deterministic chaotic attractor from a modifying the simple limit cycles dynamics of b. (d) As in c but showing infection incidence. (e–h) As in a–d, but with φ₁ = 0.75 and φ₂ = 1.5. Dynamical trends are similar to the pure ADE case, but average prevalences now differ and the limit cycles of the two strains are never now in phase.