Abstract
Identifying regions of the human genome that have been targets of positive selection will provide important insights into recent human evolutionary history and may facilitate the search for complex disease genes. However, the confounding effects of population demographic history and selection on patterns of genetic variation complicate inferences of selection when a small number of loci are studied. To this end, identifying outlier loci from empirical genome-wide distributions of genetic variation is a promising strategy to detect targets of selection. Here, we evaluate the power and efficiency of a simple outlier approach and describe a genome-wide scan for positive selection using a dense catalog of 1.58 million SNPs that were genotyped in three human populations. In total, we analyzed 14,589 genes, 385 of which possess patterns of genetic variation consistent with the hypothesis of positive selection. Furthermore, several extended genomic regions were found, spanning >500 kb, that contained multiple contiguous candidate selection genes. More generally, these data provide important practical insights into the limits of outlier approaches in genome-wide scans for selection, provide strong candidate selection genes to study in greater detail, and may have important implications for disease related research.
The continuing development of large-scale catalogs of genetic variation (Hinds et al. 2005; The International HapMap Consortium 2005) has stimulated increased interest in finding targets of positive selection, which acts to increase the frequency of advantageous alleles in a population (Carlson et al. 2005; Voight et al. 2006; Wang et al. 2006). Identifying regions of the human genome that have been targets of positive selection will provide important insights into recent human evolutionary history (Tishkoff et al. 2001; Hamblin et al. 2002; Sabeti et al. 2002; Akey et al. 2004; Bersaglieri et al. 2004; Thompson et al. 2004). In addition, as several previously identified genes with signatures of positive have been implicated in both Mendelian and complex diseases (Akey et al. 2002, 2004; Fullerton et al. 2002; Bamshad and Wooding 2003; Clark et al. 2003; Bustamante et al. 2005; Nielsen et al. 2005), finding additional genes that have been targets of positive selection may significantly impact disease related research.
The traditional paradigm for identifying genes subject to adaptive evolution has been to study a small number of loci that one hypothesizes a priori to have been under selection. However, an inherent limitation to single locus approaches is that population demographic history confounds inferences of natural selection because both processes can have similar effects on the distribution of genetic variation (Przeworski et al. 2000; Andolfatto 2001; Nielsen 2001). For example, both positive selection and increases in population size lead to an excess of low-frequency alleles in a population relative to what is expected under a standard neutral model. Therefore, rejection of the standard neutral model usually cannot be interpreted as unambiguous evidence for selection.
The recently described genome-wide catalogs of human genetic variation (Hinds et al. 2005; The International HapMap Consortium 2005), however, provide the necessary resources to move beyond single locus studies and efficiently scan the entire genome for loci that have been targets of positive selection. Genome-wide approaches provide the opportunity to begin to disentangle the effects of demography and selection. Specifically, population demographic history is a genome-wide force that affects patterns of variation at all loci in a genome in a similar manner, whereas natural selection acts upon specific loci (Cavalli-Sforza 1966; Lewontin and Krakauer 1973). Therefore, by sampling a large number of loci throughout the genome, empirical distributions of test statistics can be constructed and genes subject to locus-specific forces, such as natural selection, can be identified as outlier loci.
Although identifying outlier loci is a promising and intuitively simple approach for detecting candidate selection genes in genome-wide data sets, the efficiency of this strategy has not been rigorously evaluated. Furthermore, ascertainment bias is pervasive in many large-scale polymorphism studies (Clark et al. 2005), where single nucleotide polymorphisms (SNPs) were initially discovered in a limited number of chromosomes and subsequently genotyped in a larger sample set. Here we describe a simulation study to evaluate the performance of a simple outlier approach in ascertained data sets based on a commonly used statistic of the site frequency spectrum. We demonstrate that outlier approaches are likely to result in an enriched set of genes that have been targets of positive selection and that when levels of ascertainment bias are modest, reliable inferences of candidate selection genes can be made. Furthermore, we performed a genome-wide scan for positive selection in three human populations using a dense catalog of SNPs. In total, we analyzed 14,589 genes distributed across all autosomal chromosomes and identified 385 genes that possess patterns of genetic variation consistent with the hypothesis of positive selection. In addition, we identified several dramatic examples of selective sweeps that span >500 kb.
Results
Efficiency of a simple outlier approach in data sets with and without ascertainment bias
Positive selection is expected to result in a skew of the site frequency spectrum toward an excess of low frequency alleles relative to neutral expectations. A popular statistic to measure such skews is Tajima’s D (Tajima 1989), and significantly negative values indicate patterns of genetic variation that are consistent with either positive selection or demographic perturbations such as population expansions. One issue that arises in applying Tajima’s D to the dense catalogs of genetic variation that have been developed in humans (Hinds et al. 2005; The International HapMap Consortium 2005) is that it was originally developed for sequence and not genotype data. In general, the SNPs used in these genotyping studies were initially identified in a limited number of chromosomes (a “discovery” panel) and subsequently genotyped in a larger set of individuals (Hinds et al. 2005; The International HapMap Consortium 2005). The SNP discovery process results in an important ascertainment bias, which leads to an excess of intermediate frequency alleles in a sample, biasing Tajima’s D upwards.
Thus, it would be difficult to make inferences about the statistical significance of Tajima’s D for a single gene when only genotype data are available. However, we hypothesized that by analyzing the distribution of Tajima’s D (denoted as TDGen when applied to genotype data) across thousands of loci, candidate selection genes could potentially be identified as outliers in the extreme negative tails of the empirical distribution of TDGen. Intuitively, however, the ability to make meaningful inferences of the site frequency from TDGen, and hence identify candidate selection genes, will critically depend on the magnitude of ascertainment bias.
To test this hypothesis and to identify scenarios that are conducive to applying Tajima’s D to genotype data, we performed coalescent simulations to mimic a small-scale genome-wide analysis in data sets with and without ascertainment bias. Specifically, we simulated 1000 data sets consisting of 1000 unlinked loci with varying fractions of neutral and positively selected loci. For each locus, we calculated TDGen for varying levels of ascertainment bias by first “discovering” SNPs in ND randomly selected chromosomes (ND = 2, 4, 8, 12, 24). Discovered SNPs were then “genotyped” in a separate panel of NT chromosomes (NT = 48; see Methods), and the resulting genotypes were used to calculate TDGen. Complete ascertainment (i.e., full sequence data) was modeled by calculating Tajima’s D from all NT = 48 chromosomes. Finally, for each value of ND, we constructed an empirical distribution of TDGen and asked how many selected genes were found in either the top 1% or 5% negative tail of the empirical distribution. As a measure of efficiency, we summarized the simulation results by the positive predictive value (PPV), which is defined as the proportion of outlier loci that have been targets of selection. For example, a 1% threshold results in 10 outliers. If four of these loci correspond to selected loci, then the PPV is 0.40.
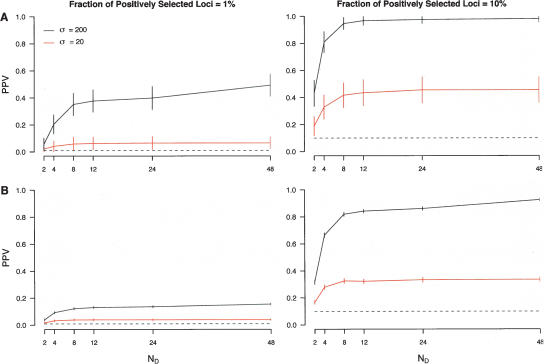
Figure 1 summarizes the simulation results and highlights several important points. First, in general, the simple outlier approach considered here does indeed result in an enriched set of genes that have been targets of selection. However, false discovery rates (FDRs) can be large and the efficiency depends on a number of parameters such as the magnitude of selection, the fraction of loci in a genome that have been targets of selection, and thresholds used to define candidate selection genes (Fig. 1). For example, even in models of complete ascertainment (corresponding to ND = 48 in Fig. 1), the PPV can be as low as 0.03 when selection is weak and the fraction of all loci in the genome subject to selection is small.
Figure 1.
Performance of a simple outlier approach in ascertained data. Patterns of polymorphism were simulated for 1000 unlinked loci consisting of varying fractions of neutral and positively selected loci (indicated at the top of each column). For each locus, 72 chromosomes were simulated and divided into discovery (24) and sample panels (48). SNP discovery was then performed by randomly selecting ND chromosomes from the discovery panel, which were then “genotyped” in the sample set, and the resulting genotypes used to calculate TDGen. The x-axis denotes the values of ND considered. Note that ND = 48 corresponds to complete ascertainment (i.e., complete sequence data). The y-axis denotes the positive predictive value (PPV) when using a threshold of either the first (A) or fifth (B) percentiles of the empirical distribution of TDGen. Horizontal dashed lines equal the expected PPV based on randomly sampling either 10 (1% threshold) or 50 (5% threshold) loci. Vertical bars indicate 95% confidence intervals. Black and red lines denote simulation results in which the scaled population selection coefficient, σ = 2Nes, for positively selected loci was 200 or 20, respectively.
Second, meaningful inferences of the site frequency spectrum can be made from genotype data when levels of ascertainment bias are not too severe (Fig. 1). However, as the number of chromosomes used for SNP discovery decreases, ascertainment bias becomes more of a barrier to accurately identifying positively selected loci using tests of the site frequency spectrum. In the extreme case when SNPs are discovered in ND = 2 chromosomes, the PPV can be substantially less compared to the PPV in unascertained data (Fig. 1), and therefore, the approach considered here would be inadvisable.
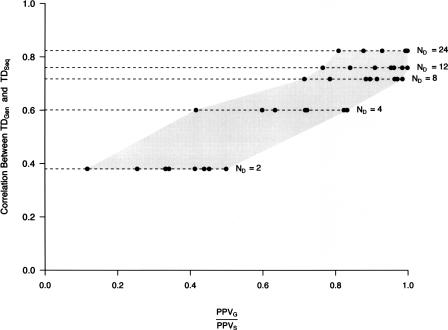
To provide practical information on whether a particular data set is or is not suitable for the outlier approach considered above, we compared the correlation between Tajima’s D derived from complete sequence (TDSeq) and genotype (TDGen) data as a function of the ratio of PPV in genotype (PPVG) to sequence data (PPVS). The ratio, (PPVG/PPVS), provides a measure of how well the results of an outlier approach in ascertained data recapitulate what would be found in data sets free of ascertainment bias. Figure 2 summarizes the results for ascertained data sets corresponding to ND = 2, 4, 8, 12, and 24. As expected, the correlation between TDSeq and TDGen increases as the number of chromosomes used for SNP discovery increases. Furthermore, when the correlation between TDSeq and TDGen increases, (PPVG/PPVS) also increases. In other words, as the number of chromosomes used for SNP discovery increases, the results of ascertained data sets approach that of complete sequence data. For example, the correlation between TDSeq and TDGen when ND = 12 is 0.79, and (PPVG/PPVS) ranges from ∼0.76–0.98 across different parameter combinations (see Fig. 2). Therefore, the correlation between TDSeq and TDGen provides a useful guide as to how suitable a particular data set is for tests based on the site frequency spectrum.
Figure 2.
The correlation between TDSeq and TDGen predicts the performance of a simple outlier approach in ascertained data sets. The correlation, r, between Tajima’s D derived from complete sequence (TDSeq) and genotype (TDGen) data was calculated from the data sets described in Figure 1. ND denotes the number of chromosomes used for SNP discovery. Discovered SNPs were then genotyped in the sample panel and used to calculate TDGen (see Fig. 1 legend). For each value of ND, there are eight points, which correspond to all combinations of simulation parameters: σ (20 and 200), fraction of positively selected loci (1% and 10%), and threshold used in defining candidate selection genes (1% and 5%). Note that for each value of ND the correlation between TDSeq and TDGen for the eight different parameter combinations differed by <1%, and thus for presentation purposes, the average correlation is shown. The gray shaded area helps to demark the range of (PPVG/PPVS) values for each value of ND and simulation parameters.
Evaluating levels of ascertainment bias in the Perlegen data set
Several large-scale polymorphism studies have recently been described in humans. Here, we evaluate levels of ascertainment bias in the Perlegen data set (Hinds et al. 2005), which consists of genotypes for ∼1.58 million SNPs that were genotyped in 71 individuals from three populations: 23 African Americans (AA), 24 Han Chinese (CHN), and 24 European Americans (EA). Perlegen SNPs were discovered by array-based resequencing of 20–50 chromosomes (Hinds et al. 2005) in a multi-ethnic panel, and are thus likely biased toward intermediate frequency alleles (see also Clark et al. 2005). To determine if the simple outlier approach described above is applicable to the Perlegen data set, we compared values of Tajima’s D for genes that overlapped with the SeattleSNPs project (http://pga.gs.washington.edu/), which is exhaustively resequencing a large number of immune and inflammatory related genes in 24 AAs and 23 EAs. This comparison is particularly informative because the SeattleSNPs and Perlegen data were derived from nearly the same set of EA and AA individuals (see Methods). We restricted our analysis of the SeattleSNPs data to a subset of 132 genes that were rigorously analyzed for signatures of selection as described in Akey et al. (2004). A significant correlation exists between TDGen and TDSeq in both populations (EA: r = 0.78, P < 10−16; AA: r = 0.56, P < 10−10) (Supplemental Fig. S1). The magnitude of the observed correlation, particularly in the EA sample, implies that the Perlegen data is suitable for identifying candidate selection genes based on the empirical distribution of TDGen.
Genome-wide analysis of the site frequency spectrum
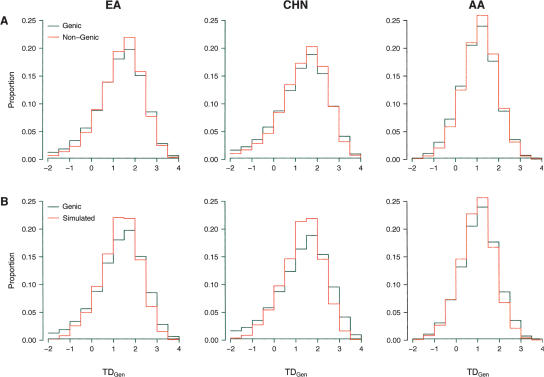
We pursed a gene-centric genome-wide scan for positive selection by identifying all Perlegen autosomal SNPs that mapped to genic regions (SNPs located within 2 kb of all known or predicted genes defined by NCBI’s build 35.1 annotation). For each sample, we calculated TDGen for all genes that contained five or more SNPs. In total, 14,589 genes possessed at least five SNPs in one or more samples, and the median number of SNPs per gene was 18, 16, and 17 for AA, CHN, and EA samples, respectively. As expected, the average TDGen in all three samples was positive (1.302, 1.335, and 1.057 for EA, CHN, and AA samples, respectively) (Fig. 3), which likely reflects the ascertainment bias introduced through the SNP discovery process. Despite the skew toward positive values, a small proportion of genes also possess sharply negative values of TDGen (Fig. 3), which is particularly interesting given the bias toward high frequency alleles in this data set.
Figure 3.
Comparing the observed distribution of TDGen to neutral expectations. The observed distribution of TDGen in genic regions compared to that observed for nongenic regions (A) and coalescent simulations (B) incorporating demographic perturbations and ascertainment bias. In modeling ascertainment bias, we considered the full range of discovery chromosomes from ND = 2 to NT, where NT = 48, 48, and 46 for the EA, CHN, and AA samples, respectively. Shown here are the simulated distributions that most closely match the observed distributions in each sample (ND = 11, 8, and 5 for the EA, CHN, and AA samples, respectively). The full details of the simulations are described in the Methods.
To determine how unusual the observed distributions of TDGen are relative to neutral expectations, two complimentary approaches were pursued. First, we compared the distribution of TDGen between genic and nongenic regions. Nongenic regions were chosen to approximate the number of SNPs found in the genic regions and allowed for linkage disequilibrium between loci (see Methods). Thus, the sampling of nongenic regions was done to approximate the complex correlation structure of the observed data. In all three samples, the distribution of TDGen was significantly different from one another (KS test, P < 10−5) and genic regions possessed more negative values of TDGen compared with nongenic regions, although the differences were less extreme in the AA sample (Fig. 3A).
Second, we performed extensive coalescent simulations that incorporated ascertainment bias under hierarchical models of SNP discovery (Akey et al. 2003; Nielsen et al. 2004). Specifically, for each sample we compared the observed and simulated distributions of TDGen under various models of ascertainment bias, where SNPs were initially discovered in ND chromosomes and subsequently genotyped in NT chromosomes (NT equals the sample size of the population under consideration). Given the uncertainty in how many chromosomes each SNP was discovered in, we considered all possible values of ND ranging from two to NT. Simulations were performed under simple models of population demographic history using parameter values that were estimated from sequence data in related populations (for a complete description of the simulations, see Methods) (Pluzhnikov et al. 2002; Akey et al. 2004).
Figure 3B shows a subset of the simulation results in each sample for the values of ND that most closely matched the observed distribution of TDGen. The complete simulation results for all values of ND are shown in Supplemental Figures S2–S4. As expected, ascertainment bias decreases as the number of chromosomes used for SNP discovery increases, which shifts the simulated distribution of TDGen toward more negative values (Supplemental Figs. S2–S4). In all samples, the proportion of genes with sharply negative values of TDGen is larger compared with the simulated data, although the differences are less pronounced in the AA sample (Fig. 3B). These results are robust to more complicated models of SNP ascertainment and alternative demographic models (data not shown). Thus, the simulations demonstrate that over a broad range of models, sharply negative values of TDGen are unusual relative to neutral expectations given the bias toward high frequency alleles in this data set. It is important to note that the coalescent simulations are obvious simplifications of human demographic history, and it is possible that more realistic models would recapitulate the observed distribution of TDGen more closely. Nonetheless, the results are consistent with the comparison of genic and nongenic loci, which does not invoke tenuous assumptions about human demographic history and models of SNP discovery.
Identifying candidate selection genes
We defined candidate selection genes as those that occur in the first percentile of the empirical distribution of TDGen in each sample. In total, 385 genes meet this criterion in one or more sample (141, 130, and 135 candidate selection genes in the AA, CHN, and EA samples, respectively) (Supplemental Table S1). The nongenic and simulated distributions of TDGen (Fig. 3) suggest that this threshold results in an enriched set of genes subject to positive selection for each sample. For example, based on the nongenic distribution of TDGen, the probability of observing 141, 130, and 135 genes in the AA, CHN, and EA samples with a TDGen ≤ Ti (where Ti is the value of TDGen corresponding to the first percentile in the ith sample) is 5.20 × 10−8, 3.4 × 10−6, and 1.34 × 10−13, respectively (binomial test). Interestingly, the median length of outlier genes versus nonoutlier genes is 29.6 kb versus 35.1 kb, which although small in magnitude is statistically significant (P = 0.0001, Wilcoxon rank sum test).
Furthermore, to obtain an empirical sense of the false-positive and -negative rates for the candidate selection genes, we compared our results to genes that overlap with the SeattleSNPs project for the EA and AA samples. Specifically, Akey et al. (2004) identified five genes (KEL, EPHB6, TRPV5, TRPV6, and DCN) with strong signatures of selection in the EA sample, three of which (TRPV5, TRPV6, and DCN) were identified in the present analysis (Supplemental Fig. S1). In the AA sample, two genes that were identified as candidate selection genes were not deemed significant in Akey et al. (2004; Supplemental Fig. S1). These results suggest that either the false-positive rate is higher in the AA sample or the results of Akey et al. (2004) were overly conservative.
An important and interesting question regarding positive selection in humans is to what extent signatures of selection are shared across populations. To address this issue, we compared the overlap in candidate selection genes among the AA, CHN, and EA samples. Following the method of Voight et al. (2006), we define a shared signature of selection as a gene that is located in the top 1% of the empirical distribution of TDGen for one sample and the top 5% for the other sample(s). Of the 213 candidate selection genes that possess data in all populations, 41% overlap between two or more samples (Supplemental Fig. S5). Thus, while our data are consistent with an accumulating number of studies reporting geographically restricted patterns of selection in humans (Stephens et al. 1998; Rana et al. 1999; Hollox et al. 2001; Tishkoff et al. 2001; Akey et al. 2002, 2004; Fullerton et al. 2002; Hamblin et al. 2002; Rockman et al. 2003; Nakajima et al. 2004; Thompson et al. 2004; Zhou et al. 2004; Carlson et al. 2005; Voight et al. 2006), many selective events are likely shared across populations.
Genomic clustering of candidate selection genes
In analyzing the distribution of TDGen across the genome (Supplemental Fig. S6), we noticed that candidate selection genes frequently occurred in clusters (defined as two or more contiguous candidate selection genes). In total, there were 30 unique clusters (14 in the EA sample, 12 in the CHN sample, seven in the AA sample, and three shared between two or more samples). These clusters encompass 81 genes, and thus 21% of all candidate selection genes are found in clusters. One potential explanation for clustering of candidate selection genes is genetic hitchhiking (i.e., the effect of positive selection on linked neutral variation) (Maynard Smith and Haigh 1974). The distance over which the signature of selection extends is a function of the strength of selection and local rates of recombination (Kaplan et al. 1989). Therefore, positive selection will leave a larger “footprint” in regions of low recombination. Supplemental Figure S6 qualitatively suggests that clusters of candidate selection genes tend to occur in regions of low recombination. Indeed, the average cM/Mb ratio in clusters of candidate selection genes is significantly lower compared with candidate selection genes not found in clusters (0.81 and 1.12 cM/Mb, respectively; Wilcoxon rank sum test, P = 0.018).
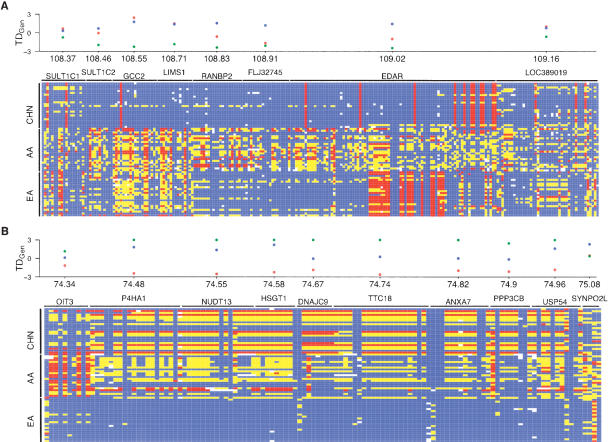
Several clusters were identified that possess striking signatures of recent selective sweeps over extended genomic regions. Figure 4 shows patterns of polymorphism across the two largest clusters. In the first region (Fig. 4A), a strong signature of positive selection was identified in the CHN sample, which spans >600 kb and includes six genes. Although our current analysis precludes definitive inferences about which gene or genes have been the target or targets of selection, EDAR is a particularly interesting candidate, as it possesses strong levels of population structure. Specifically, the average FST across all EDAR SNPs is 0.42, and 11 are >0.80 (data not shown), which is considerably higher than the well-documented genome wide average of 0.10–0.15 (Bowcock et al. 1991; Akey et al. 2002; Rosenberg et al. 2002; Shriver et al. 2004). Interestingly, several genes in the EA sample, including EDAR, also possess sharply negative values of TDGen.
Figure 4.
Strong signatures of positive selection that extend over large genomic regions. Patterns of polymorphism from the two largest clusters of candidate selection genes are shown in A and B. The regions shown in A and B are located on chromosomes 2 and 10, respectively. The signature of selection extends for >500 kb in both regions. In each panel, a graphical representation of genotypes is shown for the AA, CHN, and EA samples. Rows correspond to individuals and columns denote SNPs. For each SNP, blue, yellow, and red boxes indicate whether the individual is homozygous for the common allele, heterozygous, or homozygous for the rare allele, respectively. White boxes indicate missing data. Horizontal black bars denote the location of each gene. The distribution of TDGen for each gene is shown above the graphical representation of genotypes and the chromosomal position in Mb is shown on the x-axis (not drawn to scale). Blue, green, and red circles denote AA, CHN, and EA samples, respectively. Genes located immediately upstream and downstream of the region where patterns of polymorphism begin to approach neutrality are also shown, which helps to demark the signature of selection. Note that in A, the gene MGC10701 (Entrez gene symbol) (located between GCC2 and LIMS1) does not have genotype data available in all three samples and is not included in the figure. Similarly, in B the genes MRPS16 (located between DNAJC9 and TTC18) and ZMYND17 (located between ANXA7 and PPP3CB) are not shown, as they do not contain genotype data in all three samples. For both regions, an excess of low frequency alleles is also observed between genes (data not shown).
In the second region (Fig. 4B), a strong signature of positive selection was found in the EA sample that spans >500 kb and includes eight genes. Strikingly, variation in the EA sample has been almost completely eliminated across much of this region. Given the consistent reduction in EA polymorphism throughout the entire region, it is difficult to speculate about the potential target or targets of selection based on the available data.
Sequence analysis of candidate selection genes
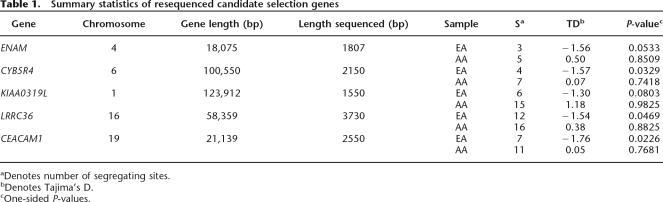
To begin to test our predictions of positive selection by more direct approaches, we selected five EA and/or CHN candidate selection genes for resequencing (Table 1). Approximately 2 kb was sequenced in each of these genes in 23 EA and 24 AA samples. All five genes were concordant with our analysis of the Perlegen data and had negative values of Tajima’s D (indicating an excess of low frequency alleles) in the EA sample and positive values in the AA sample (Table 1). The statistical significance of Tajima’s D for each gene was determined by 104 coalescent simulations assuming no recombination, conditional on the observed sample size, number of segregating sites, and demographic history using parameter values described in Akey et al. (2004). In the EA sample, the P-values of CEACAM1, LRRC36, and CYB5R4 were significant at P < 0.05 and ENAM and KIAA0319L approached statistical significance (P = 0.0533 and 0.0803). All five genes had P-values >0.10 in the AA sample. Thus, the resequencing data further support the hypothesis that the set of candidate selection genes are enriched for loci that have been subject to positive selection, although additional sequencing needs to be performed to explore the evolutionary history of these loci in greater detail.
Table 1.
Summary statistics of resequenced candidate selection genes
aDenotes number of segregating sites.
bDenotes Tajima’s D.
cOne-sided P-values.
Discussion
Outlier approaches, in which candidate selection genes are identified in the extreme tails of empirical distributions, have become a widely used strategy in genome-wide scans for selection (Akey et al. 2002; Payseur et al. 2002; Kayser et al. 2003; Storz et al. 2004; Voight et al. 2006; Wang et al. 2006). However, to our knowledge, there have been no systematic studies evaluating the performance of simple outlier approaches. To this end, we performed coalescent simulations to determine the efficiency of this study design in data sets with and without ascertainment bias. In general, we found that the simple outlier approach considered here results in an enriched set of genes that have been targets of positive selection, and meaningful inferences of the site frequency spectrum can be made from dense catalogs of genotype data when levels of ascertainment are not too severe. However, FDRs, even in completely ascertained data, can be high (Fig. 1) depending upon parameters such as the strength of selection and the fraction of all loci that have been subject to selection. Unfortunately, these parameters are generally not known and are difficult to estimate. In this regard, the utility of simple outlier approaches may seem questionable. However, if the goal of a study is to identify a restricted set of candidate selection genes to study in more detail, then our data suggest that an outlier approach is a reasonable study design as long as one accepts that a substantial proportion of candidates may be false positives.
In critically evaluating these results, it is important to note several caveats. For example, the simulations are obvious simplifications of real genomes and did not take into account variation in rates of mutation, recombination, and selection coefficients across loci, nor did they consider demographic perturbations that real populations have likely experienced. These factors are expected to increase variance and further complicate simple outlier approaches. In principle, identifying outliers conditional on mutation and recombination rates should result in more accurate inferences, although how to do this in practice warrants further investigation. In addition, we only studied one particular statistic of the site frequency spectrum, and other statistics may be more powerful. However, there is no escaping the fact that evolutionary processes are inherently stochastic and extreme outlier values arise under neutrality. Therefore, we anticipate that our general findings will extend to additional test statistics, particularly ones based on the site frequency spectrum.
Our genome-wide scan for positive selection in the Perlegen data (Hinds et al. 2005) identified 385 candidate selection genes that were outliers in the empirical distribution of TDGen. Extensive coalescent simulations and comparisons to the distribution of TDGen in nongenic regions suggests that the threshold used in defining candidate selection genes results in an enriched set of loci that have been subject to positive selection. However, it is important to note that our simulation results on the efficiency of outlier approaches demonstrate that considerable caution needs to be exercised when interpreting outlier loci as targets of positive selection as the FDR can be high (Fig. 1). The simulated and nongenic distributions of TDGen allow a rough estimate of the FDR to be made for the set of candidate selection genes in each sample. The FDR estimated from the simulations in the EA, CHN, and AA data is 0.14, 0.16, and 0.53, respectively. Based on the nongenic data, the estimated FDR in the EA, CHN, and AA data is 0.50, 0.61, and 0.60, respectively. The simulation-based estimates of the FDR are likely a lower bound as they are predicated upon simple models of human demographic history. Conversely, the nongenic-based estimates of the FDR are likely an upper bound as they assume positive selection does not occur in regions outside of genes, which is clearly a conservative assumption (see Carlson et al. 2005; Voight et al. 2006; Wang et al. 2006). Note that the FDR in the AA sample is generally larger compared with the EA and CHN samples (particularly for the simulation-based estimates), which is consistent with the comparisons to the SeattleSNPs data (Supplemental Fig. S1) and may be due to stronger ascertainment bias and/or admixture obscuring signatures of positive selection. Nonetheless, we believe that the considerable overlap of candidate selection genes across samples (Supplemental Fig. S5) and with other genome-wide analyses (see below) engenders confidence in our predictions. However, it is important to confirm these results on independent data with analyses that test different predictions of neutrality, functionally characterize suspected targets of selection, and ultimately correlate adaptive genetic variation with phenotypic variation.
A number of genome-wide scans for positive selection have recently been performed on the Perlegen and HapMap data (Carlson et al. 2005; The International HapMap Consortium 2005; Voight et al. 2006; Wang et al. 2006), which provide an important opportunity to compare results across studies. For example, in a complimentary study, Carlson et al. (2005) performed a sliding window analysis of Tajima’s D across the genome in the Perlegen data to find signatures of selection that extend over large genomic regions (≥300 kb). One or more of the candidate selection genes found in our analysis maps within 14 out of 16, 19 out of 22, and six out of seven of the EA, CHN, and AA regions, respectively, are described in Carlson et al. (2005) (note that some regions described in Carlson et al. did not contain any known or predicted genes and were omitted in these comparisons). In addition, Voight et al. (2006) developed a novel LD-based statistic (|iHS|) to detect recent positive selection and applied this test to the HapMap data. Approximately 20%, 15%, and 9% of the EA, CHN, and AA candidate selection genes are in the fifth percentile of gene-based |iHS| scores. Interestingly, if we ask how many of our candidate selection genes are within 100 kb of loci in the top fifth percentile of gene-based |iHS| scores, the overlap increases to 32%, 38%, and 27% in the EA, CHN, and AA samples, respectively. Thus, we identify many of the same genomic regions as Voight et al. (2006), although the specific genes predicted to be targets of selection varies. Moreover, Wang et al. (2006) also developed a novel LD-based test of positive selection and applied it to the Perlegen and HapMap data. Approximately 18%, 22%, and 8% of the EA, CHN, and AA candidate selection genes overlap with the genes reported as significant in Wang et al. (2006). Again, if we define an overlapping result as mapping within 100 kb of a significant gene from Wang et al. (2006) the concordance increases to 44%, 44%, and 32% for the EA, CHN, and AA candidate selection genes. Finally, five out of the 26 autosomal genes with highly differentiated nonsynonymous SNPs described in Table 9 of The International HapMap Consortium (2005) are among our candidate selection genes (EDAR, SLC30A9, HERC1, RTTN, and CEACAM1).
Although there is considerable overlap between our results and previously described genome-wide scans for positive selection, we also find evidence for selection in genes not implicated in the above-described studies. This is to be expected for a number of reasons. For example, our simulations suggest that the FDR of outlier approaches is likely to be high (Fig. 1). Furthermore, tests of neutrality generally have low statistical power. In addition, the statistical tests used in each study are likely recovering selective events from different time periods and for different stages of the selective sweep. For instance, the LD-based statistic of Voight et al. (2006) is most suitable for identifying recent, incomplete, and/or ongoing selective sweeps. Conversely, tests based on the site frequency spectrum likely have higher power to identify sweeps where the advantageous allele is approaching fixation or completed sweeps in which new mutations are occurring on selected haplotypes. As just one illustrative example, one of our strongest signatures of selection in the EA sample spans a large genomic region that includes the genes TRPV5 and TRPV6. We and others have previously shown that this region is subject to positive selection (Akey et al. 2004; Stajich and Hahn 2005). Voight et al. (2006) found no evidence for selection at TRPV5 and TRPV6 in Europeans (although this region was significant in East Asians), which can be attributed to the fact that most SNPs in this region exist as low frequency alleles and as such are “invisible” to LD-based tests that require common polymorphisms. Thus, our results complement the previously described genome-wide scans for selection.
Finally, several investigators have posited that complex disease genes may be enriched for signatures of selection (Sharma 1998; Bamshad and Wooding 2003; Akey et al. 2004), which can be regarded as an extension of the thrifty gene hypothesis proposed by Neel to explain the high prevalence of type II diabetes (Neel 1962). If this is in general true, then the genes that we have found to possess evidence of selection may be strong candidate disease genes. Furthermore, through the effects of genetic hitchhiking, which we have found several dramatic examples of, positive selection may also influence patterns of genetic variation in neutrally evolving complex disease genes. Thus, a more complete understanding of how, where, and why positive selection has acted on the human genome may facilitate the design and interpretation of disease mapping studies.
Methods
Data
Perlegen SNP genotypes (Hinds et al. 2005) were downloaded from http://genome.perlegen.com/browser/download.html, and all autosomal SNPs were retained for further analysis. These data were annotated based on NCBI’s build 35 and had rs numbers assigned according to dbSNP build 123. Therefore, we mapped all Perlegen SNPs onto dbSNP build 125. This resulted in a change of dbSNP rs identifiers for 14,608 SNPs. In addition, 1361 SNPs were discarded because they could not be uniquely mapped to the human genome. The filtered set of SNPs was mapped to known or predicted genes and pseudogenes according to NCBI build 35.1. We retained psuedogenes in the analysis because they may be in linkage disequilibrium with adjacent targets of positive selection, functional pseudogenes have been described (Jeffs et al. 1994; Hirotsune et al. 2003; Yano et al. 2004), and we wanted to increase the fraction of the genome surveyed. Recombination rates, expressed as cM/Mb, based on the deCode genetic map (Kong et al. 2002) were downloaded from http://genome.ucsc.edu/.
Data analysis
The site frequency spectrum for each gene and for each sample was assessed with the statistic Tajima's D (Tajima 1989). When applied to genotype data, we denote Tajima’s D by TDGen. To obtain the empirical distribution of TDGen for nongenic regions, we drew sets of Perlegen SNPs that mapped outside of known or predicted genes. Specifically, the length and number of SNPs for each sampled nongenic region were chosen to approximate that observed for genic regions. The number of nongenic regions sampled in each population was 12,269, 11,800, and 12,896 for the EA, CHN, and AA samples, respectively. The average TDGen for the nongenic regions in all three samples was positive and similar to the average TDGen for genic regions (1.30, 1.33, and 1.10 for EA, CHN, and AA samples, respectively).
Coalescent simulations
Coalescent simulations of positive selection (for the data presented in Figs. 1, 2) were performed with the program SelSim (Spencer and Coop 2004) assuming a stochastic trajectory of the advantageous mutation. We considered a model of an incomplete selective sweep, where the frequency of the advantageous allele has reached a population frequency of 90%. Additional parameters of the simulations were the magnitude of selection defined by the scaled population selection coefficient (σ = 2Nes = 20, 200), the population mutation rate (θ = 4Neμ = 10), and the population recombination rate (ρ = 4Ner = 10). In these formulas Ne denotes the effective population size, s the selective advantage of the beneficial mutation per copy per generation, μ the mutation rate per site per generation, and r the recombination rate per site per generation. Assuming an effective population size of 104 and a recombination rate between base pairs of 10−8/generation, this corresponds to an ∼25 kb region. For each simulation, replicate 72 chromosomes were simulated and partitioned into discovery (n = 24) and sample (n = 48) panels. SNP discovery was then performed by randomly selecting ND = 2, 4, 8, 12, 24 chromosomes from the discovery panel, which were then genotyped in the sample set, and the resulting genotypes were used to calculate TDGen. To compare these results to that expected assuming no ascertainment bias, we also calculated TDSeq from the complete set of haplotypes in the sample panel.
To determine how unusual the observed distributions of TDGen were relative to neutral expectations, we performed coalescent simulations with the program ms (Hudson 2002; obtained from R. Hudson's Web site [http://home.uchicago.edu/~rhudson1/source.html]) that incorporated mutation, recombination, population demographic history, and various models of SNP ascertainment. Specifically, for each sample we compared the empirical distribution of TDGen to the simulated distribution of TDGen conditional on the observed number of genes (NGene), gene lengths (L), segregating sites (S), and number of chromosomes (nT). The parameters of the simulation include θ = 4NeμL, ρ = 4NerL, demographic history, and SNP ascertainment. To model the uncertainty in local rates of recombination and mutation, in each coalescent replicate we sampled r and μ from a γ(2, 0.5 × 10−8) and γ(2, 10−8) distribution, respectively (Pluzhnikov et al. 2002; Akey et al. 2004). Note that the expected values of these distributions equals the genome-wide averages of r and μ, although they do not fully take into account the potentially large heterogeneity in recombination and mutation rates across the genome.
The demographic models used for the EA and AA samples are described in Akey et al. (2004). These models are particularly relevant because they were estimated from exhaustive resequencing data of 132 genes in nearly the same set of EA and AA individuals as was used in the Perlegen study. Specifically, of the 24 EA individuals in the Perlegen study, 23 overlap with SeattleSNPs. Similarly, of the 24 AA individuals used in the Perlegen study, 22 overlap with SeattleSNPs. Akey et al. (2004) performed extensive studies over a broad range of demographic models for each population and found that a bottleneck and exponential expansion was most consistent with the observed EA and AA data, respectively. The bottleneck parameters in the EA sample were nearly identical to those inferred by Reich et al. (2001) based on patterns of linkage disequilibrium. For the CHN sample, we also assumed a bottleneck model using the same parameter values as in the EA sample because the observed distributions of TDGen were nearly identical in both samples (Fig. 1). In addition, Pluzhnikov et al. (2002) found that Han Chinese populations are consistent with a bottleneck model based on sequence data from 10 noncoding loci.
SNP ascertainment was performed as described above by first simulating NT chromosomes, where NT = 48, 48, and 46 for EA, CHN, and AA samples, respectively. Next SNPs were discovered in ND randomly selected haplotypes from the NT chromosomes. Values of ND considered were ND = [2, . . . , NT]. Complete ascertainment occurs when NT = ND. Finally, the discovered SNPs were genotyped in the NT chromosomes and TDGen was calculated. For each sample and for each ND, this process was repeated NGene times, where NGene = 13,517, 12,963, and 14,349 for the EA, CHN, and AA samples, respectively. Simulation replicates that resulted in less than five discovered SNPs were discarded, as was done with the observed data, and the simulation was repeated. This SNP discovery strategy recapitulates the hierarchical nature of identifying SNPs in a small discovery panel and subsequently genotyping these ascertained markers in a larger sample. Note, however, that it does not take into account the possibility of identifying SNPs in one particular population and genotyping them in additional populations.
Sequencing
Human DNA samples were obtained from the Coriell Institute (Camden, NJ). We analyzed DNA from 24 AAs from the Human Variation Panel, African-American Panel of 50 (HD50AA) and DNA from 23 EAs derived from various CEPH pedigrees. Sequencing was performed by standard PCR-based automated sequencing using Applied Biosystem’s Big Dye terminator chemistry on an ABI 3100 or ABI 3700 (Applied Biosystems). PCR and sequencing primers were designed with custom PERL scripts by using the program PRIMER3 (Rozen and Skaletsky 2000) and are available upon request.
Acknowledgments
We thank Dayna Akey, James Ronald, Chris Carlson, Deborah Nickerson, and three anonymous reviewers for their thoughtful comments related to this work and Perlegen Biosciences for making their data publicly available. We also thank Robert Moyzis and Jonathan Pritchard for help in accessing their data and thoughtful discussions. J.M.A. is supported by research starter grants from the UW Division of Nutritional Sciences and the NSF (DEB-0512279), J.L.K. by NIH Genome Training Grant, and W.J.S. by NIH grant HD42563.
Footnotes
[Supplemental material is available online at www.genome.org.]
Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.5157306
References
- Akey J.M., Zhang G., Zhang K., Jin L., Shriver M.D., Zhang G., Zhang K., Jin L., Shriver M.D., Zhang K., Jin L., Shriver M.D., Jin L., Shriver M.D., Shriver M.D. Interrogating a high-density SNP map for signatures of natural selection. Genome Res. 2002;12:1805–1814. doi: 10.1101/gr.631202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akey J.M., Zhang K., Xiong M., Jin L., Zhang K., Xiong M., Jin L., Xiong M., Jin L., Jin L. The effect of single nucleotide polymorphism identification strategies on estimates of linkage disequilibrium. Mol. Biol. Evol. 2003;20:232–242. doi: 10.1093/molbev/msg032. [DOI] [PubMed] [Google Scholar]
- Akey J.M., Eberle M.A., Rieder M.J., Carlson C.S., Shriver M.D., Nickerson D.A., Kruglyak L., Eberle M.A., Rieder M.J., Carlson C.S., Shriver M.D., Nickerson D.A., Kruglyak L., Rieder M.J., Carlson C.S., Shriver M.D., Nickerson D.A., Kruglyak L., Carlson C.S., Shriver M.D., Nickerson D.A., Kruglyak L., Shriver M.D., Nickerson D.A., Kruglyak L., Nickerson D.A., Kruglyak L., Kruglyak L. Population history and natural selection shape patterns of genetic variation in 132 genes. PLoS Biol. 2004;2:e286. doi: 10.1371/journal.pbio.0020286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andolfatto P. Adaptive hitchhiking effects on genome variability. Curr. Opin. Genet. Dev. 2001;11:635–641. doi: 10.1016/s0959-437x(00)00246-x. [DOI] [PubMed] [Google Scholar]
- Bamshad M., Wooding S.P., Wooding S.P. Signatures of natural selection in the human genome. Nat. Rev. Genet. 2003;4:99–111. doi: 10.1038/nrg999. [DOI] [PubMed] [Google Scholar]
- Bersaglieri T., Sabeti P.C., Patterson N., Vanderploeg T., Schaffner S.F., Drake J.A., Rhodes M., Reich D.E., Hirschhorn J.N., Sabeti P.C., Patterson N., Vanderploeg T., Schaffner S.F., Drake J.A., Rhodes M., Reich D.E., Hirschhorn J.N., Patterson N., Vanderploeg T., Schaffner S.F., Drake J.A., Rhodes M., Reich D.E., Hirschhorn J.N., Vanderploeg T., Schaffner S.F., Drake J.A., Rhodes M., Reich D.E., Hirschhorn J.N., Schaffner S.F., Drake J.A., Rhodes M., Reich D.E., Hirschhorn J.N., Drake J.A., Rhodes M., Reich D.E., Hirschhorn J.N., Rhodes M., Reich D.E., Hirschhorn J.N., Reich D.E., Hirschhorn J.N., Hirschhorn J.N. Genetic signatures of strong recent positive selection at the lactase gene. Am. J. Hum. Genet. 2004;74:1111–1120. doi: 10.1086/421051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowcock A.M., Kidd J.R., Mountain J.L., Hebert J.M., Carotenuto L., Kidd K.K., Cavalli-Sforza L.L., Kidd J.R., Mountain J.L., Hebert J.M., Carotenuto L., Kidd K.K., Cavalli-Sforza L.L., Mountain J.L., Hebert J.M., Carotenuto L., Kidd K.K., Cavalli-Sforza L.L., Hebert J.M., Carotenuto L., Kidd K.K., Cavalli-Sforza L.L., Carotenuto L., Kidd K.K., Cavalli-Sforza L.L., Kidd K.K., Cavalli-Sforza L.L., Cavalli-Sforza L.L. Drift, admixture, and selection in human evolution: A study with DNA polymorphisms. Proc. Natl. Acad. Sci. 1991;88:839–843. doi: 10.1073/pnas.88.3.839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bustamante C.D., Fledel-Alon A., Williamson S., Nielsen R., Hubisz M.T., Glanowski S., Tanenbaum D.M., White T.J., Sninsky J.J., Hernandez R.D., Fledel-Alon A., Williamson S., Nielsen R., Hubisz M.T., Glanowski S., Tanenbaum D.M., White T.J., Sninsky J.J., Hernandez R.D., Williamson S., Nielsen R., Hubisz M.T., Glanowski S., Tanenbaum D.M., White T.J., Sninsky J.J., Hernandez R.D., Nielsen R., Hubisz M.T., Glanowski S., Tanenbaum D.M., White T.J., Sninsky J.J., Hernandez R.D., Hubisz M.T., Glanowski S., Tanenbaum D.M., White T.J., Sninsky J.J., Hernandez R.D., Glanowski S., Tanenbaum D.M., White T.J., Sninsky J.J., Hernandez R.D., Tanenbaum D.M., White T.J., Sninsky J.J., Hernandez R.D., White T.J., Sninsky J.J., Hernandez R.D., Sninsky J.J., Hernandez R.D., Hernandez R.D., et al. Natural selection on protein-coding genes in the human genome. Nature. 2005;437:1153–1157. doi: 10.1038/nature04240. [DOI] [PubMed] [Google Scholar]
- Carlson C.S., Thomas D.J., Eberle M.A., Swanson J.E., Livingston R.J., Rieder M.J., Nickerson D.A., Thomas D.J., Eberle M.A., Swanson J.E., Livingston R.J., Rieder M.J., Nickerson D.A., Eberle M.A., Swanson J.E., Livingston R.J., Rieder M.J., Nickerson D.A., Swanson J.E., Livingston R.J., Rieder M.J., Nickerson D.A., Livingston R.J., Rieder M.J., Nickerson D.A., Rieder M.J., Nickerson D.A., Nickerson D.A. Genomic regions exhibiting positive selection identified from dense genotype data. Genome Res. 2005;15:1553–1565. doi: 10.1101/gr.4326505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavalli-Sforza L.L. Population structure and human evolution. Proc. R. Soc. Lond. B. 1966;164:362–379. doi: 10.1098/rspb.1966.0038. [DOI] [PubMed] [Google Scholar]
- Clark A.G., Glanowski S., Nielsen R., Thomas P.D., Kejariwal A., Todd M.A., Tanenbaum D.M., Civello D., Lu F., Murphy B., Glanowski S., Nielsen R., Thomas P.D., Kejariwal A., Todd M.A., Tanenbaum D.M., Civello D., Lu F., Murphy B., Nielsen R., Thomas P.D., Kejariwal A., Todd M.A., Tanenbaum D.M., Civello D., Lu F., Murphy B., Thomas P.D., Kejariwal A., Todd M.A., Tanenbaum D.M., Civello D., Lu F., Murphy B., Kejariwal A., Todd M.A., Tanenbaum D.M., Civello D., Lu F., Murphy B., Todd M.A., Tanenbaum D.M., Civello D., Lu F., Murphy B., Tanenbaum D.M., Civello D., Lu F., Murphy B., Civello D., Lu F., Murphy B., Lu F., Murphy B., Murphy B., et al. Inferring nonneutral evolution from human-chimp-mouse orthologous gene trios. Science. 2003;302:1960–1963. doi: 10.1126/science.1088821. [DOI] [PubMed] [Google Scholar]
- Clark A.G., Hubisz M.J., Bustamante C.D., Williamson S.H., Nielsen R., Hubisz M.J., Bustamante C.D., Williamson S.H., Nielsen R., Bustamante C.D., Williamson S.H., Nielsen R., Williamson S.H., Nielsen R., Nielsen R. Ascertainment bias in studies of human genome-wide polymorphism. Genome Res. 2005;15:1496–1502. doi: 10.1101/gr.4107905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fullerton S.M., Bartoszewicz A., Ybazeta G., Horikawa Y., Bell G.I., Kidd K.K., Cox N.J., Hudson R.R., Di Rienzo A., Bartoszewicz A., Ybazeta G., Horikawa Y., Bell G.I., Kidd K.K., Cox N.J., Hudson R.R., Di Rienzo A., Ybazeta G., Horikawa Y., Bell G.I., Kidd K.K., Cox N.J., Hudson R.R., Di Rienzo A., Horikawa Y., Bell G.I., Kidd K.K., Cox N.J., Hudson R.R., Di Rienzo A., Bell G.I., Kidd K.K., Cox N.J., Hudson R.R., Di Rienzo A., Kidd K.K., Cox N.J., Hudson R.R., Di Rienzo A., Cox N.J., Hudson R.R., Di Rienzo A., Hudson R.R., Di Rienzo A., Di Rienzo A. Geographic and haplotype structure of candidate type 2 diabetes susceptibility variants at the calpain-10 locus. Am. J. Hum. Genet. 2002;70:1096–1106. doi: 10.1086/339930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamblin M.T., Thompson E.E., Di Rienzo A., Thompson E.E., Di Rienzo A., Di Rienzo A. Complex signatures of natural selection at the Duffy blood group locus. Am. J. Hum. Genet. 2002;70:369–383. doi: 10.1086/338628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinds D.A., Stuve L.L., Nilsen G.B., Halperin E., Eskin E., Ballinger D.G., Frazer K.A., Cox D.R., Stuve L.L., Nilsen G.B., Halperin E., Eskin E., Ballinger D.G., Frazer K.A., Cox D.R., Nilsen G.B., Halperin E., Eskin E., Ballinger D.G., Frazer K.A., Cox D.R., Halperin E., Eskin E., Ballinger D.G., Frazer K.A., Cox D.R., Eskin E., Ballinger D.G., Frazer K.A., Cox D.R., Ballinger D.G., Frazer K.A., Cox D.R., Frazer K.A., Cox D.R., Cox D.R. Whole-genome patterns of common DNA variation in three human populations. Science. 2005;307:1072–1079. doi: 10.1126/science.1105436. [DOI] [PubMed] [Google Scholar]
- Hirotsune S., Yoshida N., Chen A., Garrett L., Sugiyama F., Takahashi S., Yagami K., Wynshaw-Boris A., Yoshiki A., Yoshida N., Chen A., Garrett L., Sugiyama F., Takahashi S., Yagami K., Wynshaw-Boris A., Yoshiki A., Chen A., Garrett L., Sugiyama F., Takahashi S., Yagami K., Wynshaw-Boris A., Yoshiki A., Garrett L., Sugiyama F., Takahashi S., Yagami K., Wynshaw-Boris A., Yoshiki A., Sugiyama F., Takahashi S., Yagami K., Wynshaw-Boris A., Yoshiki A., Takahashi S., Yagami K., Wynshaw-Boris A., Yoshiki A., Yagami K., Wynshaw-Boris A., Yoshiki A., Wynshaw-Boris A., Yoshiki A., Yoshiki A. An expressed pseudogene regulates the messenger-RNA stability of its homologous coding gene. Nature. 2003;423:91–96. doi: 10.1038/nature01535. [DOI] [PubMed] [Google Scholar]
- Hollox E.J., Poulter M., Zvarik M., Ferak V., Krause A., Jenkins T., Saha N., Kozlov A.I., Swallow D.M., Poulter M., Zvarik M., Ferak V., Krause A., Jenkins T., Saha N., Kozlov A.I., Swallow D.M., Zvarik M., Ferak V., Krause A., Jenkins T., Saha N., Kozlov A.I., Swallow D.M., Ferak V., Krause A., Jenkins T., Saha N., Kozlov A.I., Swallow D.M., Krause A., Jenkins T., Saha N., Kozlov A.I., Swallow D.M., Jenkins T., Saha N., Kozlov A.I., Swallow D.M., Saha N., Kozlov A.I., Swallow D.M., Kozlov A.I., Swallow D.M., Swallow D.M. Lactase haplotype diversity in the Old World. Am. J. Hum. Genet. 2001;68:160–172. doi: 10.1086/316924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson R.R. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics. 2002;18:337–338. doi: 10.1093/bioinformatics/18.2.337. [DOI] [PubMed] [Google Scholar]
- The International HapMap Consortium A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffs P.S., Holmes E.C., Ashburner M., Holmes E.C., Ashburner M., Ashburner M. The molecular evolution of the alcohol dehydrogenase and alcohol dehydrogenase-related genes in the Drosophila melanogaster species subgroup. Mol. Biol. Evol. 1994;11:287–304. doi: 10.1093/oxfordjournals.molbev.a040110. [DOI] [PubMed] [Google Scholar]
- Kaplan N.L., Hudson R.R., Langley C.H., Hudson R.R., Langley C.H., Langley C.H. The “hitchhiking effect” revisited. Genetics. 1989;123:887–899. doi: 10.1093/genetics/123.4.887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kayser M., Brauer S., Stoneking M., Brauer S., Stoneking M., Stoneking M. A genome scan to detect candidate regions influenced by local natural selection in human populations. Mol. Biol. Evol. 2003;20:893–900. doi: 10.1093/molbev/msg092. [DOI] [PubMed] [Google Scholar]
- Kong A., Gudbjartsson D.F., Sainz J., Jonsdottir G.M., Gudjonsson S.A., Richardsson B., Sigurdardottir S., Barnard J., Hallbeck B., Masson G., Gudbjartsson D.F., Sainz J., Jonsdottir G.M., Gudjonsson S.A., Richardsson B., Sigurdardottir S., Barnard J., Hallbeck B., Masson G., Sainz J., Jonsdottir G.M., Gudjonsson S.A., Richardsson B., Sigurdardottir S., Barnard J., Hallbeck B., Masson G., Jonsdottir G.M., Gudjonsson S.A., Richardsson B., Sigurdardottir S., Barnard J., Hallbeck B., Masson G., Gudjonsson S.A., Richardsson B., Sigurdardottir S., Barnard J., Hallbeck B., Masson G., Richardsson B., Sigurdardottir S., Barnard J., Hallbeck B., Masson G., Sigurdardottir S., Barnard J., Hallbeck B., Masson G., Barnard J., Hallbeck B., Masson G., Hallbeck B., Masson G., Masson G., et al. A high-resolution recombination map of the human genome. Nat. Genet. 2002;31:241–247. doi: 10.1038/ng917. [DOI] [PubMed] [Google Scholar]
- Lewontin R.C., Krakauer J., Krakauer J. Distribution of gene frequency as a test of the theory of the selective neutrality of polymorphisms. Genetics. 1973;74:175–195. doi: 10.1093/genetics/74.1.175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard Smith J., Haigh J., Haigh J. The hitch-hiking effect of a favourable Ωgene. Genet. Res. 1974;23:23–35. [PubMed] [Google Scholar]
- Nakajima T., Wooding S., Sakagami T., Emi M., Tokunaga K., Tamiya G., Ishigami T., Umemura S., Munkhbat B., Jin F., Wooding S., Sakagami T., Emi M., Tokunaga K., Tamiya G., Ishigami T., Umemura S., Munkhbat B., Jin F., Sakagami T., Emi M., Tokunaga K., Tamiya G., Ishigami T., Umemura S., Munkhbat B., Jin F., Emi M., Tokunaga K., Tamiya G., Ishigami T., Umemura S., Munkhbat B., Jin F., Tokunaga K., Tamiya G., Ishigami T., Umemura S., Munkhbat B., Jin F., Tamiya G., Ishigami T., Umemura S., Munkhbat B., Jin F., Ishigami T., Umemura S., Munkhbat B., Jin F., Umemura S., Munkhbat B., Jin F., Munkhbat B., Jin F., Jin F., et al. Natural selection and population history in the human angiotensinogen gene (AGT): 736 complete AGT sequences in chromosomes from around the world. Am. J. Hum. Genet. 2004;74:898–916. doi: 10.1086/420793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neel J.V. Diabetes mellitus: A “thrifty” genotype rendered detrimental by “progress”? Am. J. Hum. Genet. 1962;14:353–362. [PMC free article] [PubMed] [Google Scholar]
- Nielsen R. Statistical tests of selective neutrality in the age of genomics. Heredity. 2001;86:641–647. doi: 10.1046/j.1365-2540.2001.00895.x. [DOI] [PubMed] [Google Scholar]
- Nielsen R., Hubisz M.J., Clark A.G., Hubisz M.J., Clark A.G., Clark A.G. Reconstituting the frequency spectrum of ascertained single-nucleotide polymorphism data. Genetics. 2004;168:2373–2382. doi: 10.1534/genetics.104.031039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R., Bustamante C., Clark A.G., Glanowski S., Sackton T.B., Hubisz M.J., Fledel-Alon A., Tanenbaum D.M., Civello D., White T.J., Bustamante C., Clark A.G., Glanowski S., Sackton T.B., Hubisz M.J., Fledel-Alon A., Tanenbaum D.M., Civello D., White T.J., Clark A.G., Glanowski S., Sackton T.B., Hubisz M.J., Fledel-Alon A., Tanenbaum D.M., Civello D., White T.J., Glanowski S., Sackton T.B., Hubisz M.J., Fledel-Alon A., Tanenbaum D.M., Civello D., White T.J., Sackton T.B., Hubisz M.J., Fledel-Alon A., Tanenbaum D.M., Civello D., White T.J., Hubisz M.J., Fledel-Alon A., Tanenbaum D.M., Civello D., White T.J., Fledel-Alon A., Tanenbaum D.M., Civello D., White T.J., Tanenbaum D.M., Civello D., White T.J., Civello D., White T.J., White T.J., et al. A scan for positively selected genes in the genomes of humans and chimpanzees. PLoS Biol. 2005;3:e170. doi: 10.1371/journal.pbio.0030170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payseur B.A., Cutter A.D., Nachman M.W., Cutter A.D., Nachman M.W., Nachman M.W. Searching for evidence of positive selection in the human genome using patterns of microsatellite variability. Mol. Biol. Evol. 2002;19:1143–1153. doi: 10.1093/oxfordjournals.molbev.a004172. [DOI] [PubMed] [Google Scholar]
- Pluzhnikov A., Di Rienzo A., Hudson R.R., Di Rienzo A., Hudson R.R., Hudson R.R. Inferences about human demography based on multilocus analyses of noncoding sequences. Genetics. 2002;161:1209–1218. doi: 10.1093/genetics/161.3.1209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Przeworski M., Hudson R.R., Di Rienzo A., Hudson R.R., Di Rienzo A., Di Rienzo A. Adjusting the focus on human variation. Trends Genet. 2000;16:296–302. doi: 10.1016/s0168-9525(00)02030-8. [DOI] [PubMed] [Google Scholar]
- Rana B.K., Hewett-Emmett D., Jin L., Chang B.H., Sambuughin N., Lin M., Watkins S., Bamshad M., Jorde L.B., Ramsay M., Hewett-Emmett D., Jin L., Chang B.H., Sambuughin N., Lin M., Watkins S., Bamshad M., Jorde L.B., Ramsay M., Jin L., Chang B.H., Sambuughin N., Lin M., Watkins S., Bamshad M., Jorde L.B., Ramsay M., Chang B.H., Sambuughin N., Lin M., Watkins S., Bamshad M., Jorde L.B., Ramsay M., Sambuughin N., Lin M., Watkins S., Bamshad M., Jorde L.B., Ramsay M., Lin M., Watkins S., Bamshad M., Jorde L.B., Ramsay M., Watkins S., Bamshad M., Jorde L.B., Ramsay M., Bamshad M., Jorde L.B., Ramsay M., Jorde L.B., Ramsay M., Ramsay M., et al. High polymorphism at the human melanocortin 1 receptor locus. Genetics. 1999;151:1547–1557. doi: 10.1093/genetics/151.4.1547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich D.E., Cargill M., Bolk S., Ireland J., Sabeti P.C., Richter D.J., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Cargill M., Bolk S., Ireland J., Sabeti P.C., Richter D.J., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Bolk S., Ireland J., Sabeti P.C., Richter D.J., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Ireland J., Sabeti P.C., Richter D.J., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Sabeti P.C., Richter D.J., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Richter D.J., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Kouyoumjian R., Farhadian S.F., Ward R., Farhadian S.F., Ward R., Ward R., et al. Linkage disequilibrium in the human genome. Nature. 2001;411:199–204. doi: 10.1038/35075590. [DOI] [PubMed] [Google Scholar]
- Rockman M.V., Hahn M.W., Soranzo N., Goldstein D.B., Wray G.A., Hahn M.W., Soranzo N., Goldstein D.B., Wray G.A., Soranzo N., Goldstein D.B., Wray G.A., Goldstein D.B., Wray G.A., Wray G.A. Positive selection on a human-specific transcription factor binding site regulating IL4 expression. Curr. Biol. 2003;13:2118–2123. doi: 10.1016/j.cub.2003.11.025. [DOI] [PubMed] [Google Scholar]
- Rosenberg N.A., Pritchard J.K., Weber J.L., Cann H.M., Kidd K.K., Zhivotovsky L.A., Feldman M.W., Pritchard J.K., Weber J.L., Cann H.M., Kidd K.K., Zhivotovsky L.A., Feldman M.W., Weber J.L., Cann H.M., Kidd K.K., Zhivotovsky L.A., Feldman M.W., Cann H.M., Kidd K.K., Zhivotovsky L.A., Feldman M.W., Kidd K.K., Zhivotovsky L.A., Feldman M.W., Zhivotovsky L.A., Feldman M.W., Feldman M.W. Genetic structure of human populations. Science. 2002;298:2381–2385. doi: 10.1126/science.1078311. [DOI] [PubMed] [Google Scholar]
- Rozen S., Skaletsky H., Skaletsky H. Primer3 on the WWW for general users and for biologist programmers. Methods Mol. Biol. 2000;132:365–386. doi: 10.1385/1-59259-192-2:365. [DOI] [PubMed] [Google Scholar]
- Sabeti P.C., Reich D.E., Higgins J.M., Levine H.Z., Richter D.J., Schaffner S.F., Gabriel S.B., Platko J.V., Patterson N.J., McDonald G.J., Reich D.E., Higgins J.M., Levine H.Z., Richter D.J., Schaffner S.F., Gabriel S.B., Platko J.V., Patterson N.J., McDonald G.J., Higgins J.M., Levine H.Z., Richter D.J., Schaffner S.F., Gabriel S.B., Platko J.V., Patterson N.J., McDonald G.J., Levine H.Z., Richter D.J., Schaffner S.F., Gabriel S.B., Platko J.V., Patterson N.J., McDonald G.J., Richter D.J., Schaffner S.F., Gabriel S.B., Platko J.V., Patterson N.J., McDonald G.J., Schaffner S.F., Gabriel S.B., Platko J.V., Patterson N.J., McDonald G.J., Gabriel S.B., Platko J.V., Patterson N.J., McDonald G.J., Platko J.V., Patterson N.J., McDonald G.J., Patterson N.J., McDonald G.J., McDonald G.J., et al. Detecting recent positive selection in the human genome from haplotype structure. Nature. 2002;419:832–837. doi: 10.1038/nature01140. [DOI] [PubMed] [Google Scholar]
- Sharma A.M. The thrifty-genotype hypothesis and its implications for the study of complex genetic disorders in man. J. Mol. Med. 1998;76:568–571. doi: 10.1007/s001090050251. [DOI] [PubMed] [Google Scholar]
- Shriver M.D., Kennedy G.C., Parra E.J., Lawson H.A., Sonpar V., Huang J., Akey J.M., Jones K.W., Kennedy G.C., Parra E.J., Lawson H.A., Sonpar V., Huang J., Akey J.M., Jones K.W., Parra E.J., Lawson H.A., Sonpar V., Huang J., Akey J.M., Jones K.W., Lawson H.A., Sonpar V., Huang J., Akey J.M., Jones K.W., Sonpar V., Huang J., Akey J.M., Jones K.W., Huang J., Akey J.M., Jones K.W., Akey J.M., Jones K.W., Jones K.W. The genomic distribution of population substructure in four populations using 8,525 autosomal SNPs. Hum. Genomics. 2004;1:274–286. doi: 10.1186/1479-7364-1-4-274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer C.C., Coop G., Coop G. SelSim: a program to simulate population genetic data with natural selection and recombination. Bioinformatics. 2004;20:3673–3675. doi: 10.1093/bioinformatics/bth417. [DOI] [PubMed] [Google Scholar]
- Stajich J.E., Hahn M.W., Hahn M.W. Disentangling the effects of demography and selection in human history. Mol. Biol. Evol. 2005;22:63–73. doi: 10.1093/molbev/msh252. [DOI] [PubMed] [Google Scholar]
- Stephens J.C., Reich D.E., Goldstein D.B., Shin H.D., Smith M.W., Carrington M., Winkler C., Huttley G.A., Allikmets R., Schriml L., Reich D.E., Goldstein D.B., Shin H.D., Smith M.W., Carrington M., Winkler C., Huttley G.A., Allikmets R., Schriml L., Goldstein D.B., Shin H.D., Smith M.W., Carrington M., Winkler C., Huttley G.A., Allikmets R., Schriml L., Shin H.D., Smith M.W., Carrington M., Winkler C., Huttley G.A., Allikmets R., Schriml L., Smith M.W., Carrington M., Winkler C., Huttley G.A., Allikmets R., Schriml L., Carrington M., Winkler C., Huttley G.A., Allikmets R., Schriml L., Winkler C., Huttley G.A., Allikmets R., Schriml L., Huttley G.A., Allikmets R., Schriml L., Allikmets R., Schriml L., Schriml L., et al. Dating the origin of the CCR5-Δ32 AIDS-resistance allele by the coalescence of haplotypes. Am. J. Hum. Genet. 1998;62:1507–1515. doi: 10.1086/301867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storz J.F., Payseur B.A., Nachman M.W., Payseur B.A., Nachman M.W., Nachman M.W. Genome scans of DNA variability in humans reveal evidence for selective sweeps outside of Africa. Mol. Biol. Evol. 2004;21:1800–1811. doi: 10.1093/molbev/msh192. [DOI] [PubMed] [Google Scholar]
- Tajima F. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics. 1989;123:585–595. doi: 10.1093/genetics/123.3.585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson E.E., Kuttab-Boulos H., Witonsky D., Yang L., Roe B.A., Di Rienzo A., Kuttab-Boulos H., Witonsky D., Yang L., Roe B.A., Di Rienzo A., Witonsky D., Yang L., Roe B.A., Di Rienzo A., Yang L., Roe B.A., Di Rienzo A., Roe B.A., Di Rienzo A., Di Rienzo A. CYP3A variation and the evolution of salt-sensitivity variants. Am. J. Hum. Genet. 2004;75:1059–1069. doi: 10.1086/426406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tishkoff S.A., Varkonyi R., Cahinhinan N., Abbes S., Argyropoulos G., Destro-Bisol G., Drousiotou A., Dangerfield B., Lefranc G., Loiselet J., Varkonyi R., Cahinhinan N., Abbes S., Argyropoulos G., Destro-Bisol G., Drousiotou A., Dangerfield B., Lefranc G., Loiselet J., Cahinhinan N., Abbes S., Argyropoulos G., Destro-Bisol G., Drousiotou A., Dangerfield B., Lefranc G., Loiselet J., Abbes S., Argyropoulos G., Destro-Bisol G., Drousiotou A., Dangerfield B., Lefranc G., Loiselet J., Argyropoulos G., Destro-Bisol G., Drousiotou A., Dangerfield B., Lefranc G., Loiselet J., Destro-Bisol G., Drousiotou A., Dangerfield B., Lefranc G., Loiselet J., Drousiotou A., Dangerfield B., Lefranc G., Loiselet J., Dangerfield B., Lefranc G., Loiselet J., Lefranc G., Loiselet J., Loiselet J., et al. Haplotype diversity and linkage disequilibrium at human G6PD: Recent origin of alleles that confer malarial resistance. Science. 2001;293:455–462. doi: 10.1126/science.1061573. [DOI] [PubMed] [Google Scholar]
- Voight B.F., Kudaravalli S., Wen X., Pritchard J.K., Kudaravalli S., Wen X., Pritchard J.K., Wen X., Pritchard J.K., Pritchard J.K. A map of recent positive selection in the human genome. PLoS Biol. 2006;4:e72. doi: 10.1371/journal.pbio.0040072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang E.T., Kodama G., Baldi P., Moyzis R.K., Kodama G., Baldi P., Moyzis R.K., Baldi P., Moyzis R.K., Moyzis R.K. Global landscape of recent inferred Darwinian selection for Homo sapiens. Proc. Natl. Acad. Sci. 2006;103:135–140. doi: 10.1073/pnas.0509691102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yano Y., Saito R., Yoshida N., Yoshiki A., Wynshaw-Boris A., Tomita M., Hirotsune S., Saito R., Yoshida N., Yoshiki A., Wynshaw-Boris A., Tomita M., Hirotsune S., Yoshida N., Yoshiki A., Wynshaw-Boris A., Tomita M., Hirotsune S., Yoshiki A., Wynshaw-Boris A., Tomita M., Hirotsune S., Wynshaw-Boris A., Tomita M., Hirotsune S., Tomita M., Hirotsune S., Hirotsune S. A new role for expressed pseudogenes as ncRNA: Regulation of mRNA stability of its homologous coding gene. J. Mol. Med. 2004;82:414–422. doi: 10.1007/s00109-004-0550-3. [DOI] [PubMed] [Google Scholar]
- Zhou G., Zhai Y., Dong X., Zhang X., He F., Zhou K., Zhu Y., Wei H., Yao Z., Zhong S., Zhai Y., Dong X., Zhang X., He F., Zhou K., Zhu Y., Wei H., Yao Z., Zhong S., Dong X., Zhang X., He F., Zhou K., Zhu Y., Wei H., Yao Z., Zhong S., Zhang X., He F., Zhou K., Zhu Y., Wei H., Yao Z., Zhong S., He F., Zhou K., Zhu Y., Wei H., Yao Z., Zhong S., Zhou K., Zhu Y., Wei H., Yao Z., Zhong S., Zhu Y., Wei H., Yao Z., Zhong S., Wei H., Yao Z., Zhong S., Yao Z., Zhong S., Zhong S., et al. Haplotype structure and evidence for positive selection at the human IL13 locus. Mol. Biol. Evol. 2004;21:29–35. doi: 10.1093/molbev/msg231. [DOI] [PubMed] [Google Scholar]