The Hitchhiking Effect of an Autosomal Meiotic Drive Gene

Abstract

Transmission-ratio distortion is a departure from a 1:1 segregation of alleles in the gametes of a heterozygous individual. The so-called driving allele is strongly selected regardless of its effect on the fitness of the carrying individual. It may then have an important impact on neutral polymorphism due to the genetic hitchhiking effect. We study this hitchhiking effect in the case of true meiotic drive in autosomes and show that it is more dependent on the recombination rate than in the classical case of a gene positively selected at the organism level.

TRANSMISSION-RATIO distortion (TRD) is a violation of Mendel's law of heredity that favors one of the alleles of a heterozygous individual, either during or after meiosis. It has long been mentioned as “segregation distortion” or “meiotic drive”; however, these terms refer to particular cases of TRD and therefore lack generality. TRD is one of the best known examples in which a selfish genetic element (also known as an ultra-selfish gene) can increase in frequency and eventually become fixed in the population regardless of its phenotypic effect, because its own fitness is partly uncoupled from that of the “host” individual (Hurst and Werren 2001). Therefore, several authors suggested that TRD systems could have a dramatic impact on linked neutral polymorphism (Buckler et al. 1999; Lewontin 1999) due to the hitchhiking effect (Maynard Smith and Haigh 1974). This has been confirmed empirically in a few cases, in particular for the segregation distorter (SD) system of Drosophila melanogaster (Palopoli and Wu 1996) and more recently for sex chromosome drive of D. simulans by Derome et al. (2004), who showed that the sex-ratio drive had induced a strong selective sweep in populations where the distorter was in high frequency. But, to our knowledge, the theoretical properties of the hitchhiking by a TRD-causing element have never been compared to the properties of the “classical” hitchhiking by a mutation positively selected at the individual level, as described by Maynard Smith and Haigh (1974) and Barton (2000). This comparison is the aim of this article.

Here, we focused on TRD due to autosomal genes. The case of sex chromosome drive might differ, because the inherent bias in sex ratio can cause cycling dynamics (Jaenike 2001; Hall 2004) and because there is no recombination between sex chromosomes in the heterogametic sex (where distortion occurs). We consider mechanisms where the fitness cost for the individual is likely to be negligible as compared to the advantage of distortion, thus allowing fixation of the driving element (see discussion). Hence, we chose to stick to the case of true meiotic drive, i.e., to a TRD that is caused by nonrandom segregation of chromosomes or chromatids during meiosis and not by destruction or inactivation of gametes after meiosis.

We considered the fates of two biallelic loci (A | a and B | b) with recombination rate r between them. At the first locus, allele A causes true meiotic drive. The segregation index k gives the probability that A is found in the gametes of an A/a individual (k = 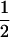in the absence of drive). We considered that the drive locus had no direct effect on the fitness of the carrying individual. The second locus B is neutral and has Mendelian segregation.

For the sake of demonstration, let us first consider the case study where distortion takes place in the whole population (no sex difference). Let x₁, x₂, x₃, and x₄ be the frequencies of genotypes AB, Ab, aB, and ab, respectively, at a given generation in the adult population. The monolocus frequencies are p, q, u, and v, for A, a, B, and b, respectively. Table 1 gives the frequencies of adult genotypes in the next generation (after random association of gametes) and the proportion of gametic haplotypes produced by each adult. Linkage disequilibrium is defined as D = x₁x₄ − x₂x₃. Using Table 1, the change in allelic frequencies at the drive locus is

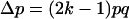(1)

and at the neutral gene

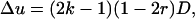(2)

which gives

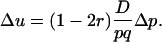(3)

TABLE 1.

Frequencies of adult genotypes after random mating and proportions of haplotypes in their gametes

		Adult genotype
AB/AB	AB/Ab	AB/aB	AB/ab	Ab/Ab	Ab/aB	Ab/ab	aB/aB	aB/ab	ab/ab
	Frequency:		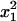2x1x2	2x1x3	2x1x4		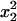2x2x3	2x2x4		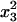2x3x4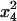
AB	1		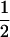k	k(1 − r)	0	kr	0	0	0	0
Ab	0		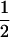0	kr	1	k(1 − r)	k	0	0	0
aB	0	0	1 − k	(1 − k)r	0	(1 − k)(1 − r)	0	1		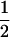0
ab		0	0	0	(1 − k)(1 − r)	0	(1 − k)r	1 − k	0		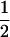1

Expression (1) is the classical result for TRD without fitness cost for the individual (Hartl and Clark 1989). The strength of selection for the distorter allele is quantified by the term (2k − 1), which equals one for complete distortion and zero for normal segregation.

The change in frequency at the neutral locus, 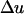, should be compared to the change induced in the classical hitchhiking case. If A* was a gene under positive selection at the individual level, so that the fitnesses were 1, 1 + s/2, and 1 + s, for genotypes a*a*, a*A*, and A*A*, respectively, the changes in allelic frequencies in one generation would be at the selected locus

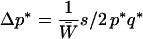(4)

and at the neutral locus

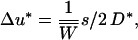(5)

which gives

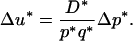(6)

By comparing Equations 3 and 6, it appears that in the case of a segregation distorter gene, there is a supplementary (1 − 2r) factor, which is specific to this kind of selection.

It is important to note that the (1 − 2r) term in (3) has nothing to do with the dynamics of linkage disequilibrium D. There is no r term in Equation 6, so the hitchhiking effect for classical diploid selection in one generation does not depend on r, but only on 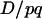. This latter term is equal to the difference of neutral allelic frequencies between the selected and counter-selected backgrounds (Barton 2000). Conversely, the hitchhiking effect in one generation in the case of segregation distortion does depend on both 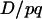and r. So, assuming that D = D*, p = p*, and Δp = Δp*, one would get

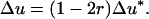(7)

Thus, everything else being equal, hitchhiking due to TRD is (1 − 2r) times weaker than classical hitchhiking.

In addition, for both cases of selection the dynamics of 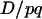from one generation to the next do depend on r. In the classical case, it is multiplied by (1 − r) at each generation of random mating if the selective coefficient s is small (Thomson 1977), which is why the final hitchhiking effect (when A is fixed) normally decreases with r. In the segregation distortion case, denoting with primes the values in the next generation, we get

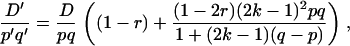(8)

which approximates as

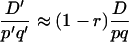(9)

for small values of (2k − 1), so the dynamics of 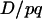have the same dependency on r as in the classical case.

We can now calculate the expected overall change in allelic frequencies at the neutral locus due to hitchhiking after the distorter allele is fixed in the population. We use the method of Barton (2000), which assumes that the selected mutation appears in a single copy in the population and thus is initially in complete linkage disequilibrium with its neutral background (considered to be allele B). Simply applying this method after extending it to the case of segregation distortion, we get

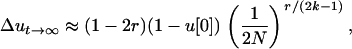(10)

where u[0] is the initial frequency of the neutral allele with which A appears. Again this exhibits a supplementary (1 − 2r) factor compared to the classical case (Barton 2000). Note that in practice the intensity of selection for the drive is likely to be much higher than the intensity of classical positive selection, so the overall hitchhiking of drive might be stronger than that of classical positive selection, except for large r. In particular, hitchhiking due to drive is always null on other chromosomes regardless of linkage disequilibrium, while classical hitchhiking is not. The approximation in Equation 10 is normally intended for small values of (2k − 1) and r, but it fits well the values computed by recursion of Equations 1 and 2 for a wider range of parameters (results not shown).

We now turn to a more realistic model in which transmission ratio is distorted in one sex only. The gametic frequencies are defined as before, except that an additional subscript refers to sexual origin (m or f for frequency in male or female gametes, respectively). Note that, as we deal with a factor that is not sex linked, the sex ratio remains constant over time. Moreover, as we neglect stochastic sampling, adult genotypes have the same frequencies within both sexes. We now define frequencies without subscripts as the mean between frequencies in male and female gametes. Indeed, if a given genotype has frequencies 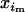and 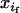in male and female gametes, its frequency in adults after random mating is x_i = ( 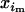+ 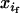)/2. More generally, the latter holds as long as the genotype studied does not affect the probability of mating. Similarly, D_m and D_f denote the linkage disequilibria in male and female gametes, respectively, whereas D is the linkage disequilibrium calculated from mean genotype frequencies. The frequencies of adult genotypes after random mating are ( 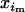× 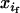) for double homozygotes and ( 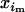× 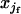+ 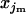× 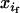) for i ≠ j. The segregation coefficients are the same as in Table 1, except that k = 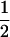in one of the two sexes. The change in allelic frequencies at the neutral locus in one generation becomes

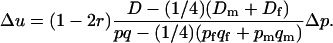(11)

The result is essentially the same as in the previous case, keeping the (1 − 2r) factor showing more dependency on recombination than in the classical case. In the rest of the equation, D (resp., pq) is replaced by the difference between its value in the whole population and the average of its within-sex values. Note that the 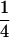factor does not depend on the sex ratio, but is simply due to diploidy.

Our results show that a meiotic drive gene has a specific effect on surrounding neutral polymorphism, which decreases more rapidly with the recombination rate than in the classical case of a gene positively selected at the organism level. This is due to the particular status of meiotic drive, owing to its place in the life cycle: it is similar to a haploid selection, but it is also dependent on characteristics of the diploid population. This particularity was emphasized by Sober and Lewontin (1982), who considered meiotic drive as one of the rare real cases of genic selection in diploids.

Note that our work does not apply to male TRD in dipterans (such as the SD system), which is somehow exceptional in that there is no recombination in the sex for which distortion occurs. Most of the described systems of this kind are maintained polymorphic in populations, and hence they do not fit our model.

The overall effect of meiotic drive elements on genomewide neutral polymorphism is of course dependent on their abundance and fixation probability, which is difficult to evaluate. There is a common opinion that most TRD systems are maintained polymorphic in natural populations. Nevertheless, several authors recently suggested that this opinion may result from a major observational bias. Indeed, only TRD systems that remain polymorphic are detected, because the driver allele does not necessarily have an otherwise phenotypic effect, and any autosomal drive effect stops after the driver allele is fixed in the population (Hurst and Werren 2001; Taylor and Ingvarsson 2003).

Postmeiotic TRD systems rely essentially on partial destruction or inactivation of gametes produced in excess (and thus are mostly restricted to males). Thus, they are often associated with a cost on viability or fertility, and so they are likely to remain polymorphic in natural populations (Charlesworth and Hartl 1978; Lyttle 1991). This could explain why the best-studied systems, such as SD in fruit flies (Sandler et al. 1959) and the mouse t-haplotype (Silver 1985), are postmeiotic TRD systems (see Lyttle 1991 for an extensive review).

In contrast, true meiotic drive elements profit from an asymmetry in the process of meiosis, such as it exists for females in many taxa, where only one meiosis product becomes an egg, and the other products degenerate into polar bodies (Pardo-Manuel de Villena and Sapienza 2001b). Hence, in true meiotic drive there is no gamete destruction, so there need not be any fertility cost (Malik 2005). The viability cost can also often be ruled out, as true meiotic drive relies on properties of the chromatin rather than on a particular coding sequence (Rhoades and Vilkomerson 1942). Hence, there is no main theoretical argument for true meiotic drive elements to remain polymorphic. Actually, Pardo-Manuel de Villena and Sapienza (2001b) stressed that the conditions required for true meiotic drive to occur are far from restrictive, and there is an increasing amount of empirical support for the importance of female meiotic drive in a wide variety of taxa, including mammals and angiosperms (see Pardo-Manuel de Villena and Sapienza 2001c, Wu et al. 2005, Fishman and Willis 2005, and Malik 2005 for recent evidence and comments or Dawe and Hiatt 2004 and Pardo-Manuel de Villena and Sapienza 2001b for reviews). Recent works using a verbal model (the “centromere drive”) even proposed that the observed rapid evolution of centromeres could be explained by recurrent meiotic drives (Henikoff and Malik 2002; Malik and Henikoff 2002; Dawe and Hiatt 2004; Malik 2005). If so, recurrent fixation of meiotic drive factors may be all but an anecdotic molecular evolutionary process (Buckler et al. 1999; Pardo-Manuel de Villena and Sapienza 2001a; Malik and Henikoff 2002; Dawe and Hiatt 2004).

Many cases of meiotic drive have been shown to occur in crosses between diverged populations (Jenczewski et al. 1997; Hall and Willis 2005; Orr and Irving 2005), and several authors suggested that meiotic drive intensity may increase with the divergence between crossing populations (Jenczewski et al. 1997; Hall and Willis 2005). If so, the level of neutral polymorphism and the linkage disequilibrium should be high in the mixed population when the drive starts, and therefore the induced hitchhiking effect should be strong. Nevertheless, this effect will be more altered by recombination than in the case of selection at the individual level.