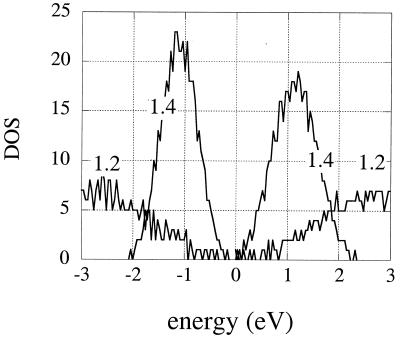
Figure 2.

The density of states for externally adding (positive energy) or removing an electron from the array, computed for a hexagonal lattice of seven sites at two different compressions, as shown. There is a 5% fluctuation in the size and another 5% fluctuation in packing. Coulombic effects are included at the Parr–Pariser–Pople level (I = 0.3 eV). This density of states is determined from the tunneling current in an STM experiment (7, 12), and the energy scale is shown in eV to conform to the experimental plots. For D/2R = 1.2, the dots are strongly coupled (cf. Fig. 1), the wave function is delocalized, the lattice is “conducting,” and the density of states (DOS) is symmetric with respect to electrons and holes. At a somewhat wider separation, shown is D/2R = 1.4, the wave function is localized (cf. Fig. 3), and the density of states is asymmetric. The symmetry of the DOS for a conducting lattice and the appearance of an asymmetric DOS for an expanded lattice are as seen in the experiments (7, 12). For even higher values of D/2R, the Hückel level computation is not reliable because the charging energy I becomes comparable with the dot–dot coupling. When D/2R is larger and the Coulomb blocking plays a more important role, the asymmetry is higher. This is understandable because the finite charging energy means that adding an electron is energetically not the mirror image of removing one, and it takes less energy to remove an electron.