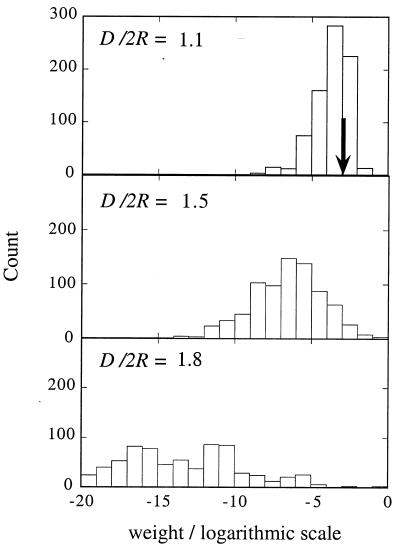
Figure 5.

A histogram of the weight, logarithmic scale, of the electronic ground state of the Hubbard Hamiltonian on the states of the noninteracting dots. Computed for a hexagonal array of seven sites, which has 784 states (ten percent wide-size distribution). The results are shown for the three electronic phases, delocalized, domain localized, and site localized, which can be successively accessed by expanding the lattice. The typical value of the weight is 1/(number of effectively participating states), and in the three regimes, this number is quite different. The value 1/784 is shown as a solid arrow in Top as it is a typical weight for the delocalized state, when all states are equally participating. The domain-localized state can be viewed as a linear combination of states of the noninteraction dots, with the number of states that contribute significantly substantially lower than the total number but somewhat larger than unity. A few weights are, therefore, large (right end of the abscicca), and most other weights are smaller than 1/784. The site-localized state can have a uniform charge distribution or a nonuniform one (see Fig. 4), but it is essentially a single state of the Hamiltonian of the noninteraction dots. One state has a weight of near unity, and all other weights are negligible.