Figure 4.

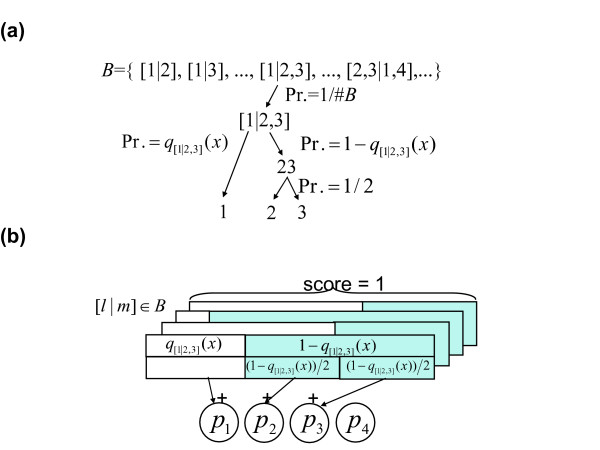
a) The probabilistic decision process of the multi-class predictor, for an example classification problem of four classes: 1, 2, 3 and 4. Firstly, one of the binary classifiers in a set B is selected with uniform probability 1#B, where #B is the number of binary targets in B. Secondly, class subset 1 or 2,3 is selected with probability q_[1|23](x) or 1 - q_[1|23](x), respectively. Thirdly, class 2 or 3 is selected with a probability of 1/2. Accordingly, one of the classes is selected with a certain probability. b) Calculation of class probability by SHS. For a binary classifier [l|m] in B and an input x which is a member of classes in l or m, we define q_[l|m](x) as an estimated probability where x is a member of class(es) in l, and the complement probability 1 - q_[l|m](x) where x is a member of class(es) in m. For example, q_[1|23](x) and 1 - q_[1|23](x) indicate the probability that x belongs to the class 1, and that x belongs to the class 2 or 3 provided that x belongs to the class 1, 2 or 3. In the SHS procedure, the probabilistic outputs by the multiple classifiers are shared and integrated by multiple classes, leading to the estimated class membership probabilities: p₁,p₂,p₃ and p₄. When l and/or m are set of multiple classes, the corresponding probabilistic outputs are shared equally to each of the members. For example, q_[1|23](x) is added to p₁, 1 - q_[1|23](x) is shared equally and added to p₂ and p₃, q_[1|234](x) is added to p₁, 1 - q_[1|234](x) is shared equally and added to p₂, p₃ and p₄, and so on for all members of B. Consequently, we obtain an estimation of multiple class probabilities p₁,p₂, p₃ and p₄ by normalizing them so that the summation p₁, p₂, p₃ and p₄ would be one.