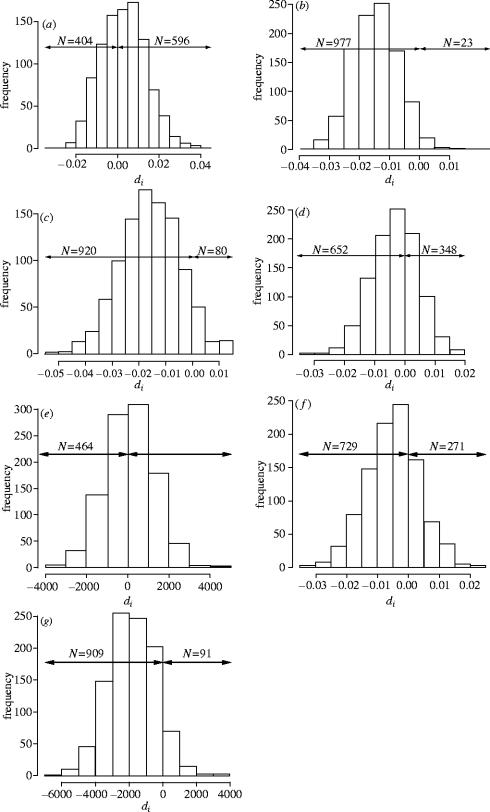
Figure 2.

Distribution of d_i for each test. d_i values are expected to be significantly greater than zero under the female-biased dispersal hypothesis. For each graph, the number of d_i values greater and lower than zero are indicated (N). (a) Genetic differentiation a_r at the local scale, $d_i={\overline{a}}_{\text{r}}{(f)}_i-{\overline{a}}_{\text{r}}{(m)}_i$; (b) genetic relatedness r_w at the local scale, $d_i={\overline{r}}_{\text{w}}{(m)}_i-{\overline{r}}_{\text{w}}{(f)}_i$; (c) genetic differentiation a_r at the regional scale, $d_i={\overline{a}}_{\text{r}}{(m)}_i-{\overline{a}}_{\text{r}}{(f)}_i$; (d) genetic relatedness r_w at the regional scale, $d_i={\overline{r}}_{\text{w}}{(f)}_i-{\overline{r}}_{\text{w}}{(m)}_i$; (e) geographic distances, $d_i=\overline{g}{(m)}_i-\overline{g}{(f)}_i$; (f) absolute residuals of the regression genetic distance/ln(geographic distance), $d_i=\overline{s}{(m)}_i-\overline{s}{(f)}_i$; (g) geographic distances of related individuals, $d_i=\overline{g}\text{rel}{(f)}_i-\overline{g}\text{rel}{(m)}_i$. ${\overline{a}}_{\text{r}}{(m)}_i$ and ${\overline{a}}_{\text{r}}{(f)}_i$ are the mean genetic differentiations a_r for males and females, respectively, for the ith resampling set; ${\overline{r}}_{\text{w}}{(m)}_i$ and ${\overline{r}}_{\text{w}}{(f)}_i$ are the mean genetic relatedness r_w for males and females respectively, for the ith resampling set; $\overline{g}{(m)}_i$ and $\overline{g}{(f)}_i$ are the mean geographic distances for males and females respectively, for the ith resampling set; $\overline{s}{(m)}_i$ and $\overline{s}{(f)}_i$ are the mean absolute values of the residuals from the regression of genetic differentiation on ln(geographic distance) for males and females respectively, for the ith resampling set; $\overline{g}\text{rel}{(m)}_i$ and $\overline{g}\text{rel}{(f)}_i$ are the mean geographic distances of related individuals for males and females, respectively.