Nanoscale Dielectrophoretic Spectroscopy of Individual Immobilized Mammalian Blood Cells

Abstract

Dielectrophoretic force microscopy (DEPFM) and spectroscopy have been performed on individual intact surface-immobilized mammalian red blood cells. Dielectrophoretic force spectra were obtained in situ in ∼125 ms and could be acquired over a region comparable in dimension to the effective diameter of a scanning probe microscopy tip. Good agreement was observed between the measured dielectrophoretic spectra and predictions using a single-shell cell model. In addition to allowing for highly localized dielectric characterization, DEPFM provided a simple means for noncontact imaging of mammalian blood cells under aqueous conditions. These studies demonstrate the feasibility of using DEPFM to monitor localized changes in membrane capacitance in real time with high spatial resolution on immobilized cells, complementing previous studies of mobile whole cells and cell suspensions.

INTRODUCTION

Dielectrophoresis (DEP) generally describes the mobility of a polarizable particle in a nonuniform electric field (1). For a particle in a vacuum, dielectrophoretic forces result in attraction of the particle toward the region of higher field gradient. For a particle suspended in a medium, the net effect of DEP can be either attractive or repulsive toward the regions of higher field gradient depending on the polarizability of the particle relative to the medium in which it resides. Because of this competition, the magnitude and sign of the force exerted on a particle depend sensitively on the frequency-dependent dielectric permittivities of the solution and the particle as well as the gradient of the squared electric field. The frequency-dependent properties of DEP have made it a useful tool in the characterization (2–6) and separation (7–9) of cells. To cite just one recent example, DEP has been used to identify and separate cancerous and healthy cells from the elevated membrane capacitance of cancerous cells (8,9).

Virtually all previous DEP studies of biological systems have been performed using fixed electrodes and mobile particles in which DEP forces were used to manipulate and measure whole particles (2–4,8–16). However, these previous techniques required mobile particles in suspensions and only yielded the average DEP properties of the whole cell or many cells (i.e., did not possess subcellular characterization capabilities). The requirement that the particles be suspended also precludes direct DEP characterization of intact tissues. In this work, the measurement configuration is reversed relative to typical dielectrophoretic analysis methods. The particles themselves are immobile, and the force on a mobile electrode is measured. Unlike direct current (DC) and quasi-DC (i.e., at or below the resonance frequency of the cantilever) scanning probe methods (17–19) for characterizing local electrical properties, dielectrophoretic force microscopy (DEPFM) depends sensitively on the alternating current (AC) frequency, allowing for dielectrophoretic spectroscopy measurements with high spatial resolution.

The dielectric properties of erythrocyte membranes are of particular interest due to the involvement of red blood cell membranes in a number of diseases such as sickle cell anemia (20), spherocytosis (21), and malaria (13). In a malarial parasitization of an erythrocyte, changes in the protein composition of the cell membrane cause a detectable difference in the dielectric properties of the cells (8,22). Previous work has shown that red blood cells had greater membrane conductivity in the radio frequency range when they have been infected with a malaria parasite (22). Additionally, the membranes of red blood cells are of key importance in erythrocyte function due to the oxygen transport duties of the cell. The most abundant protein in the red blood cell membrane is the band three protein, also known as AE1 (23), which transports bicarbonate into and out of the red blood cell. Current methods for the analysis of living blood include antibody testing (24), fluorescence-based optical microscopy, (25) and measurement of blood cell sedimentation time (26). High resolution analysis of blood cells has been performed with freeze fracture atomic force microscopy (27) and electron microscopy (23). However, real time analysis with those methods is not yet possible. Optical methods of analysis have been limited by the diffraction limit of light (28). Furthermore, these methods generally do not yield information directly related to the membrane activity (e.g., membrane capacitance, charge mobility, etc.).

The goal of this work is to investigate structurally stable immobilized erythrocyte cells by the combination of DEP with the feedback mechanism of an atomic force microscope (AFM) and further develop a theoretical model for an AFM coupled with DEP forces. The dielectric properties of the blood cell can be tested, and the information gained can be used to perform noncontact in situ imaging of the erythrocyte cell.

THEORY

The average dielectrophoretic force acting upon a homogenous particle in solution is given to be (1,29)

(1)

In Eq. 1, F is the time averaged force, ν_part is the volume of the particle, ω is the frequency of the applied waveform, ɛ_s is the dielectric constant of the solution, E is the electric field, and K is the frequency-dependent Clausius-Mossotti factor. DEPFM is influenced by the frequency of the applied waveform and the tip-sample distance.

Frequency dependence of DEPFM

When a time-varying electric field is used, K can be approximated (29) by the following expression for a spherical cell with an intracellular permittivity of ɛ_c.

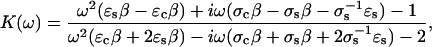(2)

where β = C_m (cell radius)/(σ_sσ_c), in which C_m is the capacitance of the cellular membrane per unit of surface area, σ_s is the conductivity of the solution surrounding the cell, and σ_c is the conductivity within the cell. The real part of K is limited to between −0.5 and 1.0.

Distance dependence of DEPFM

The image contrast in DEPFM can be interpreted using a damped driven oscillator model for describing the cantilever motion in the presence of a distance-dependent DEP force (30). Attractive and repulsive forces between the oscillating tip and the substrate lead to changes in amplitude and phase between the driving forces and the mechanical oscillation of the cantilever (30,31). For a cantilever initially oscillating on resonance, a DEP force will result in a damping in the cantilever amplitude and an increase in apparent height for both attractive and repulsive interactions. The corresponding phase change can be evaluated from expressions derived from magnetic force microscopy to describe the phase of oscillation in the presence of a spatially varying force (32):

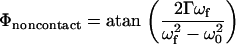(3)

In Eq. 3, ω_f is the resonance frequency of the in the presence of a perturbative force, ω₀ is the resonance frequency of the cantilever without the applied force, and Γ is the damping coefficient of the cantilever (related to the quality factor). The resonant frequency ω_f can be approximated by the following equation (33):

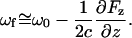(4)

The term F_z describes the vertical component of the force along the surface normal (z) in the direction of the tip. From Eqs. 3 and 4, an attractive force scaling inversely with distance from the surface is predicted to yield a negative phase shift.

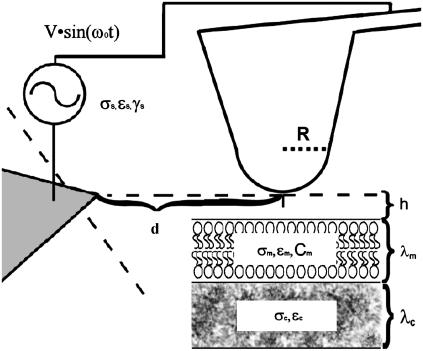
The distance dependence of the DEP force influences many of the key experimental parameters that contribute to image contrast in DEPFM. In this study, a planar counterelectrode was positioned perpendicular to the z axis of the AFM tip as seen in Fig. 1, in which R is the radius of curvature of the tip. The voltage difference across and distance between the nadir of the tip and the counterelectrode are V and d. The configuration used here differs significantly from that utilized in previous DEPFM studies, in which a grounded conducting substrate with a thin insulating overlayer served as the counterelectrode to an electrically charged tip (30,31). This configuration has the advantage of minimizing long-range attractive forces along the axis of cantilever motion resulting from capacitive charging of the tip. Although theoretical models for describing this previous configuration are well established (30,34–37), fewer predictive models are available for describing the configuration used in this study. An approximate solution designed to recover the distance dependence of DEP for a tip adjacent to a dielectric medium is described below.

FIGURE 1.

Diagram of the tip-sample geometry used to generate a dielectrophoretic force on the sample; R is the radius of curvature (∼35 nm), d is the distance between the AFM tip and the counterelectrode, σ is conductivity, h is the height of the AFM tip over the membrane, C is the capacitance, ɛ is the permittivity, γ is the viscosity, and λ is the thickness of a given medium, with the subscripts m, c, and s referring to membrane, cytosol, and solution, respectively. The distance to the counterelectrode (25–100 μm) from the AFM tip is ∼25–100 μm.

The magnitude of the electric field in any direction near the nadir of the tip, approximated by a sphere in vacuum, is given to be (38)

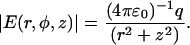(5)

The origin (r, z = 0) is the center of the sphere defined by the radius of curvature (∼35 nm), q is the total charge on an equivalent point at the center of the sphere, and ɛ₀ is dielectric permittivity of a vacuum. Only the force components directed along the z axis were used for AFM feedback. In a homogeneous medium with a dielectric constant of ɛ_s, the gradient of the electric field squared along the z axis is given to be

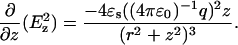(6)

For a low conductivity medium, to a first order approximation, the distance dependence of the force acting on the tip can be estimated by an integration of the attractive and repulsive forces of each volume element. This approximation neglects to include local perturbations to the electric field from the adjacent volume elements (which may be substantial) but can still be reasonably expected to recover qualitative trends of DEP in dielectric systems. The interaction between the tip and each differential volume element (dν_part) of the surrounding medium where the force contribution from each element is given to be

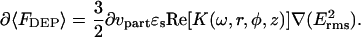(7)

From Eq. 7, the average DEP force for the system shown in Fig. 1 can be approximated to be

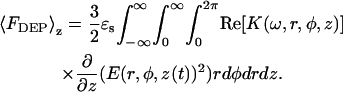(8)

The integration in Eq. 8 is performed over a semiinfinite bulk suspension medium, a thin insulating membranous slab (thickness = λ_m), and a semiinfinite bulk cytosolic slab (thickness = λ_m). A time average over the electric field is also implied. Assuming that coupling effects between adjacent materials are minimal, the total dielectrophoretic force can be written as

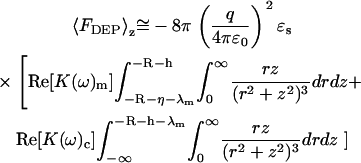(9)

In Eq. 9, h is the height of the tip over the membrane (i.e., the distance along the z axis between the minimum of the tip and the top of the membrane). A uniform dielectric constant is assumed within each medium, yielding a Clausius-Mossotti factor dependent only on frequency. The integration from (−R −h) ≤ z < ∞ for the aqueous medium is omitted, as the Clausius-Mossotti factor is zero. Integration yields the following approximate expression for the distance dependence of the dielectrophoretic force:

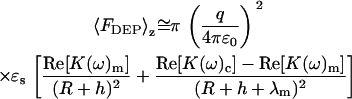(10)

In the limit of λ_m ≪ R, h, Eq. 10 simplifies to the following approximate form.

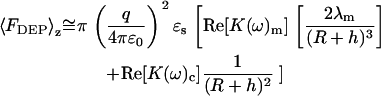(11)

Depending on R, h, and the Clausius-Mossotti factors K(ω) _m and K(ω)_c from Eq. 2, the distance dependence of the dielectrophoretic force is predicted to range from 1/h³ to 1/h. For small tip-sample separations (i.e., h ≪ R), the distance dependence of the DEP force is predicted to scale with ∼1/h for both contributions in Eq. 11 whereas for distances approaching or exceeding the radius of curvature, a distance dependence ranging from 1/h² and 1/h³ is predicted.

Explicit force calculations

A summation of the gradient of the electric field squared acting upon the cell was performed using a Maxwell 3D Field Simulator (Ansoft, Pittsburgh, PA) to estimate the magnitude and distance dependence of the dielectrophoretic force acting upon the tip in the current measurement configuration. Calculations were performed for a 5-nm-thick membrane with a dielectric constant of 5 ɛ₀ and a conductivity of 0.3 mS/m (2,4,39), a cell cytoplasm 200-nm thick with a dielectric constant of 70 ɛ₀, and a conductivity of 360 mS/m (4,5,39). The surrounding solution was assumed to have a dielectric constant of 81 ɛ₀ and a conductivity of 10 mS/m (4,5,8).

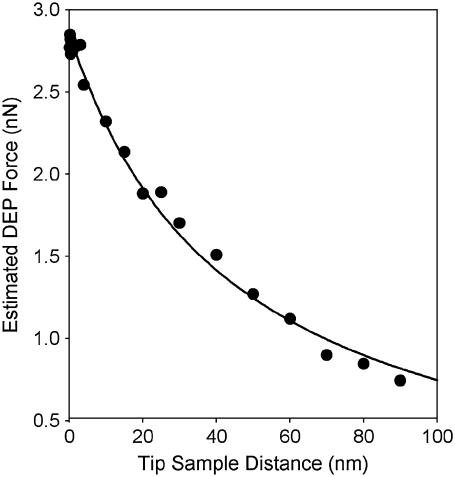
The AFM tip was modeled by two spheres of radii 35 nm and 100 nm stacked upon each other with a cone connecting the midsections of the two spheres for a total height of 330 nm. The cell membrane and cytoplasm were approximated with stacked cylinders 1 μm in diameter. The counterelectrode was represented by a sphere of radius 1 μm at a distance of 20 μm orthogonal to the z axis of the tip. A voltage difference of 10 V was applied between the tip and the counterelectrode. Using these parameters, the dielectrophoretic force acting upon the tip was predicted to be on the order of a few nN and to scale with 1/h (Fig. 2). These calculations are in good agreement with the distance dependence predicted by the approximate analytical model and are in good quantitative agreement with the forces routinely detected by atomic force microscopy (40).

FIGURE 2.

The magnitude of the DEP at various tip-sample distances obtained directly from finite element analysis calculations for a DC electric field is compared to the trend predicted from Eqs. 1 and 2 (λ_m = 5 nm, ɛ_m = 5, σ_m = 0.3 mS/m, λ_c = 200 nm, ɛ_c = 70, σ_c = 360 mS/m, ɛ_s = 81, σ_s = 10 mS/m, V = 10 V, and D = 20 μm). The conical AFM tip was modeled by two stacked spheres of radius 35 nm and 100 nm with a cone connecting the midsection of the two spheres. The fit to the data points indicated that the force acting upon the surface relative to the tip-sample distance could be approximated as 137 nN nm/(z + R) − 0.2 nN.

METHODS

A Dimension 3100 AFM (Veeco, Santa Barbra, CA) with a fluid mount was used for all imaging. Electrically conductive Pt- and Ti-coated AFM tips (μmasch, Portland, OR) with a spring constant of ∼1 nN/nm and a resonant frequency of 6–8 kHz in solution were used. All imaging was performed using tapping mode in which the cantilever was oscillated near its resonance frequency. The fluid cell of the Dimension 3100 microscope was modified so that an electric potential could be applied directly to the AFM tip. A more detailed description of the instrument can be found in previous publications (30,31). Both height and phase images were acquired.

The following procedure was used to circumvent complications associated with long-range capacitive electrostatic attraction between the cantilever and the counterelectrode (19,34,35). Each glass slide used as a substrate had a planar silver electrode constructed on it by spin coating a layer of silver colloid liquid (Ted Pella, Redding, CA, 0.02–0.05 Ω per square at a 25-μm coating thickness). Once the silver layer had cured, a sharp electrode (radius of curvature <10 μm) was created by mechanical etching. The planar silver electrode on the glass slide was connected to ground, and electrical potentials were applied to the AFM tip. In this manner, the long-range electrostatic forces between the cantilever and the counterelectrode were all orthogonal to the imaging z axis of the instrument. Before imaging, the electrical resistance between the AFM tip and the counterelectrode was measured to insure that electrical shorts had not occurred.

Erythrocyte cells were imaged while submerged in sucrose solution. Fixed sheep blood cells (Sigma Aldrich, St. Louis, MO) were attached to a glass surface that had been coated with a thin layer of polyethylenimine (PEI) (Sigma Aldrich, M_w= 1300 Da). The cells were allowed to sediment for 10 min to ensure attachment to the surface. The unattached cells were removed by washing the surface with an aqueous 8% by mass sucrose solution, consistent with previous protocols (8–10,13,41,42). A low ionic strength sucrose solution was used to minimize Joule heating while maintaining a level of tonicity similar to that of plasma to maintain blood cell integrity. The electrical resistance between the tip and the counterelectrode was typically measured to be between 1 MΩ and 3 MΩ.

To verify the integrity of the erythrocyte cells after washing, pearl chaining experiments (i.e., bunching of adjacent cells along the field lines from induced dipole-induced dipole interactions) were performed by the application of a 50-kHz 20-V_pp potential between the AFM tip and the counterelectrode. Erythrocyte cells with ruptured membranes would not be expected to exhibit strong pearl chaining, as their intracellular permittivity would be similar to that of the surrounding solution (7,12). Observations were made with a 10× magnification objective optical microscope integrated into a Dimension 3100 AFM (Fig. 1 of the Supporting Information).

The instrument response to changes in force was characterized through voltage-dependent studies at a fixed frequency (1.5 MHz). The tip responses (measured by the differences in apparent height and phase) were tested by varying the peak to peak voltage. The potential was modulated every 6 ms between 0 V_pp, and a test voltage swept from 0 V_pp to 20 V_pp.

Dielectric spectra were acquired both on and off erythrocyte cells. The reported spectra were generated by monitoring changes in the amplitude and phase of oscillation of the cantilever as the frequency of the waveform applied to the AFM tip was increased from 50 kHz to 1950 kHz 20 V_pp. For each line scan of the AFM tip, four complete frequency sweeps of the applied waveform were performed. The total time of a raster scan was ∼1 s (∼1/2 s for the trace, and ∼1/2 s for the retrace), such that a complete frequency sweep of the applied waveform was done roughly every 125 ms. The start of the frequency sweeps was synchronized with the start of the raster pattern to facilitate signal averaging along the slow-scan axis. As the frequency of the applied waveform test frequency was increased from 50 kHz to 1950 kHz, the waveform was modulated between 50 kHz and the test frequency at a rate ∼10 times faster than the frequency sweep. The modulation allowed for the creation of a baseline value to help mitigate the effects of 1/f noise. Using this approach, 1024 dielectric spectra were obtained in each complete raster scan. The average dielectric spectra were normalized to the maximum and minimum phase angles to correct for subtle drift in the amplitude of the cantilever response for multiple measurements of multiple cells.

There is evidence that cells and cell membranes can be damaged by prolonged exposure to intense electric fields, either by electroporation (43–45) or by peroxide generation at the cellular membrane due to lipid peroxidation. Previous studies of erythrocyte suspensions (46) in AC electric fields have suggested that there may be peroxide generation at the cellular membrane due to lipid peroxidation (47) when high voltages (>5 V) are applied to the electrode at AC frequencies of <10 kHz. If such a process were occurring, it would be expected that the surface of the cell would become modified over time. As part of the experiments that were done, the same erythrocyte was imaged for over an hour without a noticeable change in nanoscale surface structure.

Dielectrophoretic imaging was performed by the application of a fixed frequency (20 V_pp 1.5 MHz) to the AFM tip while the microscope was completing a raster scan. As in previous studies, dielectrophoretic forces were only applied on alternating raster scans along the slow-scan axis to separate contributions from changes in topography from changes in DEP force (30,31). Power spectral density analysis was performed on the images of erythrocytes that were acquired in both the presence and absence of AC electric fields.

RESULTS AND DISCUSSION

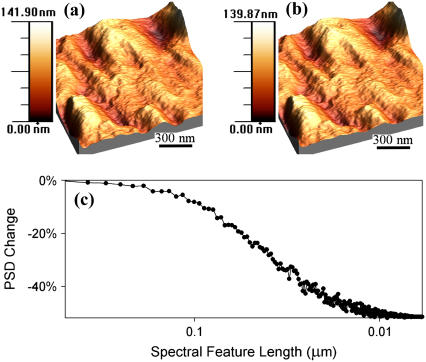
To assess the capabilities of DEPFM for local dielectric characterization of cells and tissues, it is important to first determine the degree to which the measurements themselves perturb the system under study. Images of a 1.5 μm × 1.5 μm region of a fixed red blood cell (sheep) are shown in Fig. 3, acquired both in the absence (a) and presence (b) of an AC (1.5-MHz 20-V_pp) electric field. The images were constructed with 512 raster scan lines of an AFM, with the DEP being applied on alternating lines. The lateral separation of the lines in which DEP was applied was <4 nm. The erythrocytes exhibited shapes consistent with previous measurements of cells strongly bound to surfaces (48,49). Cursory inspection did not reveal significant qualitative differences between the two images. In both cases, there were features that spanned the length of the image with a typical width of ∼200 nm.

FIGURE 3.

Topographic image of a blood cell (a), the corresponding measured topography in the presence of a DEP force (b) (20 V_pp, 1.5 MHz), and the difference in power spectral density (PSD) for the two images (c). The horizontal plane of the image is 1.5 μm × 1.5 μm and the vertical ranges of both images were 140 nm. The high-resolution images of blood cells acquired in (a) and (b) were qualitatively similar, but significant loss in PSD in the high spatial frequency regime was observed in topographic images of erythrocytes acquired in the presence versus absence of an AC electric field.

The nanoscale structural features observed in the high-resolution topographs of the red blood cells are likely due to the cell cytoskeleton. By utilizing a surrounding solution that was not carefully isotonically matched with the interior of the erythrocyte, an osmotic pressure was exerted on the cell. It is reasonable to expect the osmotic pressure to slightly deform the red blood cells, revealing the submembrane structure of the cell. The features that were observed in both images were approximately five times the length of a typical actin filament as measured by AFM (50) but similar in size to features observed by previous groups that were conjectured to be conglomerations of actin/spectin fibers resulting from changes in the structure or size of the cell (51–53).

Quantitative analysis of the two images shown in Fig. 3, A and B, can be made by examining the differences in power spectral density of the images (30). Fig. 3 C shows the difference in the spectral power of an erythrocyte topograph measured with and without an applied DEP force. The spectral powers corresponding to spatial wavelengths > ∼50 nm were similar in the two images, but significant loss in the short-wavelength components was observed upon application of the DEP forces. A decrease in spectral information at small length scales is indicative of an increase in the effective radius of curvature for the tip, consistent with noncontact imaging (30). In addition to minimizing surface deformation and damage, noncontact imaging of relatively soft cells and tissues also minimized short-range chemical adhesion forces between the tip and the extracellular matrix, as described in previous work (30).

The loss of high spatial frequencies in the DEPFM image should not necessarily be interpreted as a loss in spatial resolution. The relationship between the changes in spatial resolution and the actual displacement of the cantilever from the cell surface depends on many factors, including the aspect ratio of the surface being imaged, the effective radius of the tip, the relative strength of the field-induced DEP force as a function of position, and the ambient noise (35,36). For example, single atom resolution can be routinely observed in samples with low aspect ratios using tips with typical radii of curvature of ∼20 nm (54). By comparison with electrostatic force microscopy, the maximum resolution of electrostatic force microscopy is predicted to be ∼ 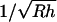, corresponding to independent determination of the electrical charges of two regions separated by ∼5 nm for a 25-nm tip radius 1 nm from the surface (55). Direct relationships between the loss of high spatial frequencies in DEPFM and the corresponding changes in spatial resolution should be made cautiously.

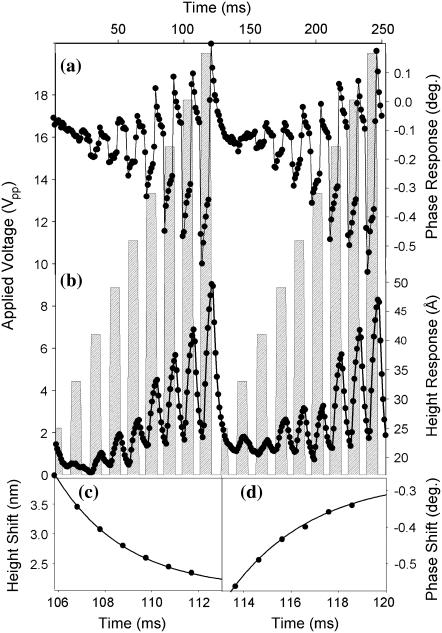
Before acquiring and interpreting dielectric spectra, the instrument response was characterized through voltage-dependent studies at a fixed frequency (1.5 MHz), shown in Fig. 4. Differences in apparent height and phase are presented as functions of the peak to peak voltage (averaged over 250 continuous waveform amplitude sweeps). The measured differences in amplitude (Fig. 2 of the Supporting Information) and phase of the cantilever scaled quadratically with the amplitude of the applied waveform, consistent with previous measurements (1,29).

FIGURE 4.

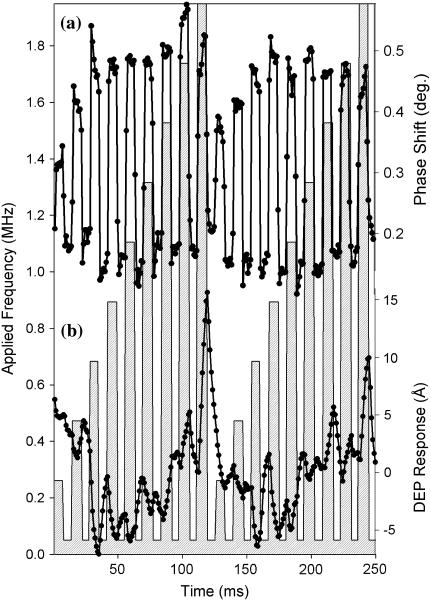
The instrument response to a change in DEP force was assessed by application of a 1.5-MHz waveform at varying amplitudes. The experimental DEP phase (a) and height (b) responses are shown as solid circles, connected by straight lines. The peak to peak voltage of the applied waveform is indicated by the crosshatched bar chart. One complete modulated voltage ramp was performed in 125 ms. Representative exponential fits of the time-dependent change in apparent height (c) and phase (d) yielded time constants of 2.7 ms and 3.1 ms, respectively.

Interestingly, the initial maximum response in phase occurred significantly faster than the change in apparent height. Fitting a representative decay section (106–112 ms) to single exponentials yielded similar time constants of ∼3 ms (2.8 ms and 3.1 ms for the amplitude and phase responses, respectively) as seen in Fig. 4, C and D. Several possible explanations for this trend were considered.

Similar time dependences in polarization-induced forces have been reported by Salmeron from localized time-dependent surface charging associated with ion motion (56). However, for an AC field of 1.5 MHz used in the measurements shown in Fig. 4, no average net increase or decrease of surface charge from ion mobility would be expected over a millisecond timescale.

A more likely explanation is that the decays observed in height and phase in Fig. 4 are a consequence of the finite response time of the instrument, either through a fundamental limitation of the cantilever mechanical motion or through the electronic limitations directing feedback. Based on previous work by Butt and co-workers, the limiting mechanical response time of the tips that were used in these studies can be estimated to be < ∼0.5 ms, and therefore was likely not responsible for the observed decays (57). Based on previous studies of fast scanning methods done in contact mode, the decay observed may be caused by the response time of the feedback loop used to transduce changes in apparent height (58). The minimal response time of a differential feedback scheme optimized for fast scanning of a Veeco Nanoscope IIIa AFM controller was reported in previous work to be ∼1 ms (58), which is comparable to the measured values of ∼3 ms. Therefore, the ∼3-ms components in the amplitude and phase response are attributed to the timescale for implementation of height changes associated with the maintenance of instrument feedback (with concomitant changes in phase). The fast component (i.e., faster than the sampling time of ∼0.5 ms) of the measured cantilever phase response to changes in DEP force in Fig. 4 A likely arose from the fundamental limits of mechanical cantilever motion (i.e., <∼0.5 ms).

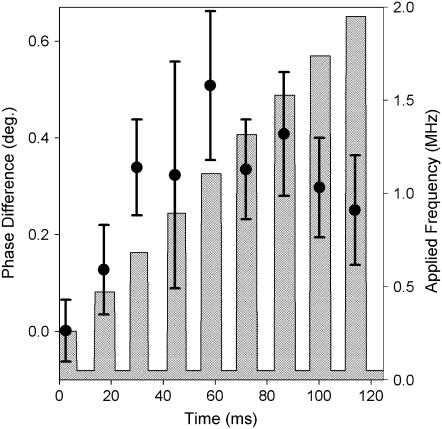
The measured changes in apparent height and phase on an erythrocyte in response to varying the frequency of a 20-V_pp applied waveform are presented in Fig. 5. The figure contains the average changes in apparent height and phase from ∼250 frequency sweeps. The crosshatched bar chart illustrates the frequency of the applied waveform, with a baseline reference frequency of 50 kHz. An increasingly positive phase shift was observed between the reference and the test waveforms, reaching a plateau of ∼0.4° at ∼850 kHz. Clear trends in the height response to the varying applied waveform were less obvious, suggesting a subtle decrease in apparent height at low test frequencies (<∼1.3 MHz) switching to relative increases at higher frequencies. Whereas the phase response is a direct measure of the change in cantilever motion, the changes in apparent height are recorded as the difference in the z-position of the piezo to maintain constant amplitude of cantilever oscillation. As a consequence, the height data are more complicated to directly relate back to the DEP spectra because the absolute z-position of the tip was also changing throughout the measurement due to topographic changes.

FIGURE 5.

Frequency-dependent DEP of a single erythrocyte in water, in which the frequency of a 20-V_pp applied waveform was modulated between a reference frequency of 50 kHz and a test frequency varied from 250 kHz to 1950 kHz (indicated by the vertical bars). The measured phase (a) and height (b) responses are shown as solid circles connected by straight lines (averages of ∼250 measurements).

The frequency modulation spectrum of the erythrocytes shown in Fig. 5 also exhibits some evidence of the exponential decays described in Fig. 4. In both the voltage and frequency modulation experiments, the changes in the apparent height occurred on comparable timescales (∼3 ms). However, the time-dependent changes in phase were much less pronounced in the frequency modulation experiments. The differences in the phase measurements acquired for voltage versus frequency modulation can be accounted for by noting the differences in tip-sample separations in the two cases. A ∼5-nm change was observed in the voltage modulation spectra, and the maximum tip-sample separation was ∼1 nm in the frequency studies. If the decay of the phase response was a result of the AFM increasing the tip-sample separation then it is reasonable to suggest that significant phase decays would only accompany large changes in the tip-sample distance. The large difference in the phase decay with changes of only a few nanometers in the tip-sample separation provides further evidence that the DEP forces probe highly localized interactions at the cellular membrane.

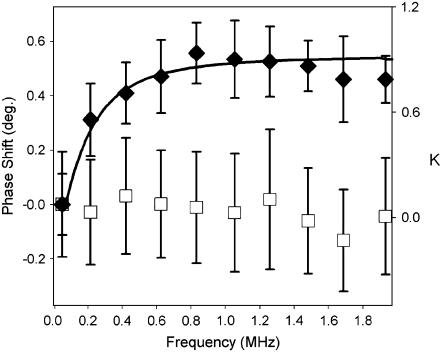
DEP spectra can be generated from the differences in phase (or height) acquired as a function of the AC frequency. A single-scan DEP spectrum of an erythrocyte is shown in Fig. 6 and was generated from the phase differences between the test and reference frequencies as depicted in Fig. 5. The complete single-scan spectrum was acquired in only 125 ms. By comparison, traditional methods for DEP spectral acquisition, in which the motion of a particle is used to transduce the interaction, often require several minutes for reliable detection at a single AC frequency (59). The average of ∼30 dielectrophoretic force spectra acquired over three different erythrocytes is shown in Fig. 7, along with the blank measurements acquired on the PEI-coated substrate. The spectra were generated from the frequency-dependent phase shifts, as shown in Fig. 5 A. The changes in phase were fit to the expected DEP forces for a cell modeled as a uniform sphere with a thin outer membrane (Eqs. 1 and 2). The model for DEP response yielded a membrane capacitance of the erythrocyte of 3.0 μF/cm² (assuming literature values of σ_c = 336 mS/m, ɛ_c = 60ɛ₀, σ_s = 10 mS/m, ɛ_s = 81ɛ₀) (2,4,5). The values for the average membrane capacitance obtained by DEPFM are in excellent agreement with capacitance measurements made by previous groups of 2.98 μF/cm² of erythrocytes in whole blood diluted with sucrose solution (60).

FIGURE 6.

A single-scan frequency-dependent dielectric spectrum of an erythrocyte in solution acquired in 125 ms. A 20-V_pp applied waveform was modulated between a reference frequency of 50 kHz, and a test frequency varied from 250 kHz to 1950 kHz (indicated by the vertical bars), as illustrated in Fig. 5. The DEP spectrum is shown as the difference in phase shift relative to the 50-kHz reference frequency. Error bars represent the standard deviation of approximately seven points at each frequency, consistent with the data shown in Fig. 5.

FIGURE 7.

Average dielectrophoretic spectra of erythrocytes in water (solid triangles), measured by changes in phase. Reference DEP spectra of the bare PEI-coated glass substrate (open squares) are also shown for comparison. Error bars represent 1 standard deviation for N = 3 cells and N = 30 measurements of the bare substrate. The error bars indicate the variation in DEP spectra across different erythrocyte cells. The solid line represents a fit of the DEP spectrum to Eq. 2 with a membrane capacitance of 3.0 μF/cm² (CM indicated the real part of the Clausius-Mossotti factor). For the fit, it was assumed that ɛ_c = 60, σ_c = 366 mS/m, ɛ_s = 81, and σ_s = 10 mS/m, consistent with previous models for thin-shelled mammalian cells (2,4,5). DEP spectra were normalized before averaging to correct for systematic drift between measurements.

CONCLUSIONS

In vitro dielectrophoretic spectroscopy of intact mammalian blood cells has been performed by DEPFM. Individual spectra were obtained in as little as 125 ms and could be acquired over a region comparable in dimension to the effective diameter of the AFM tip. Good agreement was observed between DEP spectra obtained from multiple cells and predictions using a single-shell model for predicting DEP forces. Assuming appropriate values for the intracellular and extracellular permittivities and conductivities, the membrane capacitance was calculated to be 3.0 μF/cm², which is in excellent agreement with values obtained from previous bulk measurements of cell assemblies. These studies demonstrate the feasibility of using DEPFM to characterize localized membrane capacitance in real time with high spatial resolution on immobilized cells and tissues. Such capabilities suggest new opportunities to monitor dynamic changes in cellular electrophysiology in single cells and in cell assemblies induced by external chemical or physical perturbation as a function of position and/or time.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.