Figure 2.

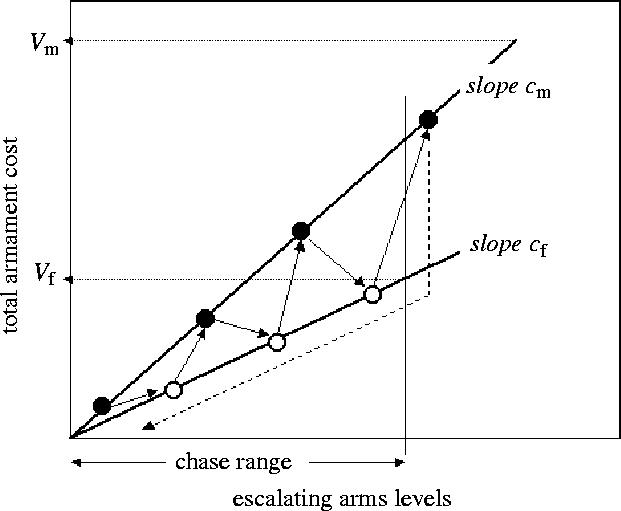
The evolutionary chase in the sexual arms race model (Parker 1979). Total arms costs are plotted against arms levels for the two sexes: at a given point on the x-axis, the total arms for each sex are exactly balanced so that the chances of winning the conflict are random, otherwise the sex with the higher arms level wins. In this example, the value of winning for females (V_f) is lower than that for males (V_m), and the slope of the total costs with escalating arms levels is lower for females (slope c_f) than for males (slope c_m). If females start at a low arms level, males can win by a slightly greater level, which females can then outbid, and so on. As arms levels escalate, females would first reach the point where their total arms costs equal their value of winning: males can still outbid them and achieve a positive payoff. At this point females do better to reduce their arms to zero, which allows males also to reduce to a very low level. The cycle then begins again.