Modelling biological complexity: a physical scientist's perspective

Abstract

We discuss the modern approaches of complexity and self-organization to understanding dynamical systems and how these concepts can inform current interest in systems biology. From the perspective of a physical scientist, it is especially interesting to examine how the differing weights given to philosophies of science in the physical and biological sciences impact the application of the study of complexity. We briefly describe how the dynamics of the heart and circadian rhythms, canonical examples of systems biology, are modelled by sets of nonlinear coupled differential equations, which have to be solved numerically. A major difficulty with this approach is that all the parameters within these equations are not usually known. Coupled models that include biomolecular detail could help solve this problem. Coupling models across large ranges of length- and time-scales is central to describing complex systems and therefore to biology. Such coupling may be performed in at least two different ways, which we refer to as hierarchical and hybrid multiscale modelling. While limited progress has been made in the former case, the latter is only beginning to be addressed systematically. These modelling methods are expected to bring numerous benefits to biology, for example, the properties of a system could be studied over a wider range of length- and time-scales, a key aim of systems biology. Multiscale models couple behaviour at the molecular biological level to that at the cellular level, thereby providing a route for calculating many unknown parameters as well as investigating the effects at, for example, the cellular level, of small changes at the biomolecular level, such as a genetic mutation or the presence of a drug. The modelling and simulation of biomolecular systems is itself very computationally intensive; we describe a recently developed hybrid continuum-molecular model, HybridMD, and its associated molecular insertion algorithm, which point the way towards the integration of molecular and more coarse-grained representations of matter.

The scope of such integrative approaches to complex systems research is circumscribed by the computational resources available. Computational grids should provide a step jump in the scale of these resources; we describe the tools that RealityGrid, a major UK e-Science project, has developed together with our experience of deploying complex models on nascent grids. We also discuss the prospects for mathematical approaches to reducing the dimensionality of complex networks in the search for universal systems-level properties, illustrating our approach with a description of the origin of life according to the RNA world view.

Life is not some sort of essence added to a physico-chemical system but neither can it simply be described in ordinary physico-chemical terms. It is an emergent property which manifests itself when physico-chemical systems are organized in particular ways. John Habgood (1994)

1. Introduction

The recent 50th anniversary of the discovery of the structure of DNA serves as a reminder of the power of reducing a system to its smallest possible components and then studying them. In a mere half-century, there has been an enormous growth in both molecular biology and genetics, the Human Genome Project being but one of many fruits (The International Human Genome Mapping Consortium 2001; Venter et al. 2001). We now understand the molecular basis of inheritance and how the symptoms of certain diseases are caused by changes in the action of one or more proteins owing to mutations in the genes encoded by the DNA itself. Yet, although reductionism is powerful, its scope is also limited. This is widely recognized in the study of complex systems whose properties are greater than the sum of their constituent parts. In this article, we review the application to biology of the concept of complexity, a modern approach to addressing integration in the sciences and engineering.

Complexity is the study of the behaviour of large collections of simple, interacting units, endowed with the potential to evolve with time (Coveney & Highfield 1996). Reductionism has given us a deep understanding of these simple units, whether they are atoms, proteins or cells, but it is equally important to study how these units interact. As the writer Alvin Toffler so succinctly described, ‘One of the most highly developed skills in contemporary Western civilization is dissection: the split-up of problems into their smallest possible components. We are good at it. So good, we often forget to put the pieces together again’ (Toffler 1984). Fortunately, a more integrative view has begun to establish itself in both the physical and biological sciences over the past 30 years or so (Kohl et al. 2000; Coveney 2003b).

A certain mutuality between, and order of application of, reductionism and complexity (‘put[ting] the pieces back together again’) is implied; we can only use an approach based on complexity if we first understand the simple units whose interactions we shall model. This is usually described as an integrative approach. We emphasize that we are not arguing against reductionism, rather that it is now time to more closely embrace the integrative approach (and therefore the concept of complexity) in all areas of science, engineering and medicine.

The recent growth of interest in systems biology reflects the increasing importance that integrative approaches are being accorded in the biological sciences. Systems biology ‘…does not investigate individual genes or proteins one at a time, as has been the highly successful mode of biology for the past 30 years. Rather, it investigates the behaviour and relationships of all of the elements in a particular biological system while it is functioning. These data can then be integrated, graphically displayed, and ultimately modeled computationally’ (Ideker et al. 2001). A recent article examines the concept of complexity within the physical sciences (Coveney 2003b). Clearly, there is a significant overlap between the approaches now being taken in the physical and biological sciences.

The purpose of the present paper is to examine complexity and systems biology from the perspective of a physical scientist. The article is structured as follows. In §2, we shall introduce some key concepts before investigating in §3 what we mean by ‘modelling’ in more detail. Although we can often describe biological systems using differential equations, we illustrate how it is usually difficult to determine all the required parameters and then to solve the set of equations. Two examples from the biological sciences (heart dynamics and circadian rhythms) are presented in §4. In §5 we describe several modern approaches drawn from the physical sciences that reproduce aspects of the flow of complex fluids. These models serve to illustrate certain similarities and differences between the approaches taken in the biological and physical sciences. Given the importance of molecular biology, the modelling of biomolecular systems is of central interest to biology; we describe in §6 some of the problems faced and how coupled or hybrid multiscale models may both alleviate these and allow the calculation of parameters necessary for the construction and study of cellular multiscale models. All of these approaches require large amounts of computational power. In §7, we discuss the potential of computational grids and the progress made to date in developing them into usable and powerful tools for all forms of computational science including computational systems biology. Finally, a theoretical method for contracting large-dimensional sets of differential equations, of the type arising in descriptions of biological networks, is described in §8, followed by its application to an investigation of the possible origin of the RNA world.

2. Integrating across length- and time-scales

The biological sciences are subdivided into a large number of fields, each of which is typically concerned with studying behaviour over a small range of length-scales—for example, molecular biology, cell biology, physiology and zoology. These fields form a rich, natural hierarchy of description and, in common with the other sciences, there is a central and unifying need to connect behaviours on different time- and length-scales, thereby integrating the different disciplines. For example, the aim of the Physiome Project (Hunter & Borg 2003), an ambitious systems biology programme, is ‘the quantitative description of the functioning organism in normal and pathophysiological states’ (Bassingthwaighte 2000). This requires the vertical integration of many biological disciplines from pathology and physiology to cellular and molecular biology. To achieve this goal, models operating at different length-scales need to be integrated into a whole that can, for example, correlate a disease symptom with genetic mutations. This is clearly an immensely challenging and open-ended research programme, which is generally regarded as being more difficult than the Human Genome Project (Kohl et al. 2000). The paradigmatic, and hitherto most successful, example of this type of project is the study of the electrophysiological behaviour of the mammalian heart (Kohl et al. 2000; Noble 2002), which we shall discuss in more detail in §4.

Fracture mechanics provides an excellent example from the physical (in this case, Earth) sciences where one has to deal with everything from the breaking of chemical bonds at a fracture tip to the propagation of macroscopic fractures (Abraham et al. 2002). The flow of complex fluids is another notoriously difficult problem to model given the inherent inhomogeneities within the system and the large range of length- and time-scales over which phenomena are observed. In §5, we describe several recent mesoscopic models that are able to reproduce such physical phenomena. Perhaps the widest separation between characteristic length-scales is the explanation of the anisotropies in the temperature of the cosmic microwave background in terms of fluctuations in the density of the primordial soup of particles (Hu 1997). The wide range of length-scales that all these phenomena and systems inhabit requires us to embrace the concept of complexity and to use integrative multiscale approaches.

2.1 Self-organization and emergence

An approach based on complexity provides a means to integrate across length- and time-scales by studying the emergence of larger scale phenomena from the interaction of units at smaller length-scales. Such complex phenomena are often self-organizing: ‘Self-organisation is the spontaneous emergence of non-equilibrium structural organisation on a macroscopic level, due to the collective interactions between a larger number of (usually simple) microscopic objects’ (Coveney & Highfield 1996). Such structural organization may be spatial, temporal or spatio-temporal in nature and is an emergent property. A system is required to be both dissipative and nonlinear for it to exhibit self-organization. Most organisms meet these criteria, as they are non-equilibrium dynamical systems and avoid equilibrium (i.e. death) through the relentless ingestion and dissipation of energy by their metabolism.

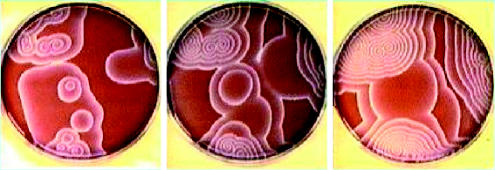
Reaction–diffusion equations are nonlinear, dissipative mathematical models (Murray 1993) that were first studied by Alan Turing (1952). They can describe many interesting complex phenomena from animal coat patterns to the behaviour of chemical oscillators, for example, the Belousov–Zhabotinsky reaction (see figure 1). They are systems of partial differential equations (PDEs) of the form

$$\frac{\partial \mathit{u}}{\partial t}=K{\mathrm{\nabla }}^2\mathit{u}+\mathit{F}(\mathit{u}),$$ (2.1)

where K is the diagonal matrix of non-negative definite constant diffusion coefficients and the vector quantity u(x, t) describes the spatio-temporal behaviour of a set of dependent variables, such as the concentration of chemicals, which themselves are interacting according to generally nonlinear rate processes F(u). Turing recognized that these simple systems of equations could describe morphogenesis, the process controlling shape, structure and function in living beings.

Figure 1.

Three separate snapshots of the spatial evolution of the Belousov–Zhabotinsky reaction.

Perhaps unsurprisingly, many biological systems can be well described by sets of differential equations. However, studying mathematical models, such as reaction–diffusion equations, is frequently difficult as the nonlinearities usually prevent us from applying straightforward analytical mathematical tools (Zwillinger 1997). There are, as always, several ways of proceeding which we shall discuss in §3.3, but before doing so, let us define what we mean by a model itself.

3. What do we mean by a scientific ‘model’?

A model is an abstraction of reality with which we can make predictions that may be tested by experiment. A model may be simple, for example, the logistic equation describing how a population of bacteria grows (Murray 1993), or as complicated as the Physiome Project aims to be. A mathematical model makes predictions, whereas statistical models enable us to draw statistical inferences about the probable properties of a system.

3.1 Deductive and inductive models

When building a model, one must choose between two fundamentally different philosophies of science, as espoused by Popper and Bacon (Chalmers 1994). If the prediction is necessarily true given that the model is also true, then it is said to be a Popperian (deductive or falsifiable) model. Alternatively, if the prediction is statistically inferred from observations, then the model is Baconian (inductive).

Deductive models contain a mathematical description (e.g. the reaction–diffusion equations) that makes predictions about reality. If these predictions do not agree with experiment, then the validity of the entire model may be questioned. This approach dominates the physical sciences, and hence physical scientists are inclined to adopt its methods and assumptions unquestioningly. However, it is illuminating to consider the Baconian philosophy as both philosophies are widely used in the biological sciences.

An inductive model uses a statistical method to infer from a set of observations a prediction whose success is measured by its comparison to previously unseen data. There is a natural shift from using inductive to deductive models as our theoretical understanding improves. However, it is important to recognize that some systems may not yield to an adequate theoretical description; even if they do, then extracting predictions from the associated deductive model may be intractable. Therefore, we can expect to have to rely on inductive models in some areas of science for some time to come.

The use of both deductive and inductive models in the biological sciences is partly attributable to the more complicated nature of biological systems. It is also a result of the rapid adoption of automation by experimental biologists, which has led to the vast and ever-expanding production of biological data. High-throughput experimentation has revolutionized several biological disciplines; consider the impact of microarrays on the genetic sciences (Lander 1999) and of the development of combinatorial chemistry on the search for and discovery of new drugs in the pharmaceutical industry. While equally intractable problems exist within the physical sciences, for example, discovering high-temperature superconductors, equivalent approaches are being developed more slowly (Evans et al. 2001). The more equal footing of Popperian and Baconian approaches within the biological sciences can lead to tension between their respective practitioners. From a practical, (not to say utilitarian) point of view, both approaches are required to advance our current understanding of biological systems.

3.2 Multiscale modelling

Just as one cannot perform a single experiment that simultaneously investigates all the length-scales of a biological system, one cannot generally expect to produce a single model that spans all the length- and time-scales of interest. A conceptually simple solution is to construct a chain of models such that the output of one model is the input of another. One can apply this approach in two broadly different ways.

In a hierarchical multiscale approach, the model at the shortest length-scale is run to completion before its results are passed to the model describing the next level. ‘Effective theories’ can be used to bridge the gap between these different scales, and one can therefore arrange for a suitable matching of parameters at different levels. However, if there is significant feedback—that is, if changes at the larger length-scale affect behaviour at the smaller length-scale—then this approach is no longer valid and we must use a hybrid or coupled multiscale approach where schemes are constructed with the physics, chemistry or biology dynamically coupled across the length- and time-scales involved. Computationally, it is simple to envisage many nested models forming a single multiscale model in a manner similar to a set of Russian matryoshka dolls. However, care must be taken to minimize the error introduced by each model, as errors will be compounded. For example, fluctuations in a particulate region must be correctly transferred to a continuum region within a multiscale model, and vice versa (Delgado-Buscalioni et al. 2005).

Hierarchical modelling is usually associated with deductive approaches, although following the dynamics of a protein whose structure has been predicted using homology modelling is an example of combining both inductive and deductive approaches in a simple hierarchical approach (Giordanetto et al. in press). Although the concept is simple, it is generally very difficult to construct a computational multiscale model; yet such models have huge potential to describe biological systems. The Physiome Project has adopted a hierarchical multiscale approach (Bassingthwaighte 2000; Hunter & Borg 2003), which, as the component models exchange information infrequently, simplifies enormously the problem of constructing the interface between models. Consequently, the view persists that the main challenge in multiscale modelling is standardizing the format of the information exchanged between models using, for example, the Systems Biology Markup Language (sbml.org), an application of eXtensible Markup Language (XML). An alternative approach is exemplified by Finkelstein et al. (2004) who present a metamodel that stretches beyond simply model exchange and which emphasizes the key role of abstraction in multiscale modelling. In our opinion, the main challenge is the scientific one of dynamically coupling the models involved.

In §4, we shall briefly describe the progress made in modelling a specific organ—the mammalian heart—and how the existing models could form part of a larger multiscale model. The nascent development of multiscale modelling for the study of biomolecular systems is discussed in §6.

3.3 Models of biological systems

Many biological systems can be described well by deductive models, often as a scheme of coupled nonlinear differential equations, congruent with our earlier definitions of both systems biology and complexity. Metabolic networks or signal transduction pathways provide canonical examples of biochemical systems that can be described using differential equations.

Sets of coupled, nonlinear ordinary differential equations (ODEs) or PDEs cannot usually be solved analytically, although there are cases where solutions exist or approximations can be made (e.g. Zwillinger 1997). In some specific cases, it is possible to systematically contract the set of equations to produce a simpler description that retains some universal features of the dynamics. A specific example of this, as applied to the evolution of self-replicating RNA sequences, is discussed in §8. If, as is often the case, both these approaches fail, then one must numerically solve the equations and is therefore required to know large numbers of (e.g. rate) coefficients that enter the equations as free parameters. Whereas some advocates of systems biology believe that given sufficient automation and other resources, it will eventually be possible to determine all these parameters, others are more sceptical. Assuming unknown parameters continue to exist, one empirical option is to ‘tune’ them to reproduce biologically reasonable behaviour, although such an ad hoc procedure is clearly unsatisfactory. A further option is to calculate the unknown parameters using another model. Depending on the degree of integration between the two models, this approach furnishes an illustration of either hierarchical or hybrid multiscale modelling.

4. Two examples from the biological sciences: heart dynamics and circadian clocks

The electromechanical behaviour of the heart (Kohl et al. 2000; Noble 2002) has been successfully modelled using differential equations. This has been, and remains, a particularly rich vein for systems biology. Studying organs whose behaviour is more directly driven by chemical processes, for example, the liver (Finkelstein et al. 2004), is more complicated than the heart and is consequently at an earlier stage. A further example is the development of systems biology models to study the growth of tumour cells (Alarcón et al. 2004).

The size and behaviour of the system, the mammalian heart, defines one set of length- and time-scales and the choice of the subunit, the cardiac myocytes, defines a second, smaller and shorter, set of length- and time-scales. Creating and simulating a sufficiently detailed model of the individual cells and their interactions (in terms of ion fluxes) allows the scientist to both reproduce the behaviour of the organ and to connect the heart's behaviour to that of its individual cells. The UK Engineering and Physical Sciences Research Council (EPSRC) funded e-Science pilot project called ‘Integrative Biology’ (www.integrativebiology.ac.uk), in which one of us is a co-investigator, is attempting to build much of the software and hardware infrastructure to support such research worldwide (Gavaghan et al. in press).

Extending this connection down to the behaviour of the ion channels (modelled with atomistic detail) is a significant challenge, but one that can be expected to bring large benefits (Hunter & Borg 2003). To illustrate this, compare modelling the dynamics of a heart and a Formula One racing car. The dynamics of each system can be described by differential equations but, crucially, the rhythmic behaviour of the heart varies significantly with tiny changes at the molecular level, for example, a genetic mutation in a key protein or the absence or presence of one or more molecules (including drugs). There is no analogue for this sophisticated dependency in a Formula One car. Some progress can be made without a hybrid multiscale model by inferring changes in the cellular behaviour through the examination of the effect of genetic mutations on a single ion channel (Hunter & Borg 2003), a crude form of hierarchical modelling. To properly integrate biomolecular detail into the existing electromechanical models of the heart will, however, require a hybrid multiscale approach.

Establishing direct connections between individual protein–protein interactions and cardiovascular dynamics is necessary to investigate the effects of different genetic mutations on the behaviour of the organ (Noble 2002). Additionally, as drugs are designed at the molecular level, this connection would enable the effect—intended or otherwise—of the drug to be understood at the level of the whole organ. This in turn would open up the possibility of in silico screening of drug candidates; furthermore, connecting heart dynamics down to the molecular level would put the cellular model on a more solid footing, because it should permit the calculation of unknown rate coefficients within membrane-based electrophysiological models.

A new project funded by the UK's Biotechnology and Biological Sciences Research Council (BBSRC), called ‘Integrative Biological Simulation’, in which one of us (P.V.C.) is a co-investigator, aims to investigate the behaviour of monotopic enzymes through the use of multiscale models to couple coarse-grained, atomistic and even electronic structure models. Unlike transmembrane proteins, monotopic enzymes are bound to only one side of cellular membranes. The comparative lack of experimental data (the structures of only a few monotopic enzymes are known), their novel association with cellular membranes and the importance of their enzymatic functions ensures that this class of proteins is interesting to study. Perhaps the best-known monotopic enzyme is prostaglandin H2 synthase, often referred to as ‘COX’ (Picot et al. 1994). This protein is inhibited by non-steroidal anti-inflammatory drugs (NSAIDs), such as aspirin and ibuprofen (Garavito & Mulichak 2003). Designing new NSAIDs with diminished side effects remains an important goal for the pharmaceutical industry.

Slower than the beating of the heart, circadian clocks oscillate with periods close to 24 h and allow organisms to adapt their behaviour to a changing environment (Goldbeter 2002). A complicated network of interacting proteins, RNA and genes produces these oscillations and the experimental picture of these networks, while incomplete, is steadily improving.

Much progress has been achieved in understanding circadian clocks by describing them as systems of nonlinear ODEs. These have become progressively more complicated as additional experimental data has become available (Goldbeter 2002; Leloup & Goldbeter 2003). A recent study by Rand et al. (2004) suggests that such networks must be complex enough to ensure that the system has the flexibility to simultaneously satisfy several different requirements, for example, compensating for changes in environment such as pH or temperature. The nonlinearities enter through molecular feedback mechanisms. Negative feedback, usually in the form of a protein inhibiting the expression of its gene, has been shown to be necessary to reproduce oscillations and although positive feedback is also often encountered, recent computational studies have shown that it is not essential (Becker-Weimann et al. 2004).

Few of the existing circadian models contain experimentally determined parameters; the values of the parameters are usually tuned to fit the observed behaviour (Rand et al. 2004). Despite this, theoretical models have been able to predict birhythmicity, a previously unobserved dynamical phenomenon (Goldbeter 2002). Birhythmicity results from the occurrence of two stable limit cycles separated by an unstable cycle. In addition, the disruption (or otherwise) of the mouse circadian clock by the mutation of key genes has been reconciled with existing models (Becker-Weimann et al. 2004). There is also speculation about possible links between genetic mutations and known circadian clinical conditions (Goldbeter 2002; Leloup & Goldbeter 2003).

The existing models are often described as ‘molecular’ (Rand et al. 2004), yet they coarse-grain the action of each enzyme's catalytic processes to a single rate constant. In common with whole-organ heart models, there would be a large benefit in coupling the existing models to true atomistic models of the individual biomolecular components. This would allow both the calculation of unknown model parameters and the investigation of the effects of genetic mutation. This would simultaneously give the existing theoretical models more credibility and allow the investigation of the possibly non-intuitive effects of more subtle genetic changes. The construction of such hybrid multiscale models will be discussed in §6.

5. A pedagogical example from the physical sciences: complex fluids

As a basis for comparison and to illustrate the concepts introduced thus far, consider the modelling of complex fluids, a ‘simpler’ case from the physical sciences. Complex fluids are fluids in which processes occur on a range of different length- and time-scales. Paradigmatic cases include binary immiscible fluids and surfactant-containing fluids (Coveney 2003a). In the past 15 years or so, a radically new way of studying fluid dynamics has emerged in keeping with our definition of complexity. Rather than using conventional numerical methods such as a continuum fluid dynamics (CFD) algorithm to solve macroscopic PDEs, the approach is predicated upon determining the fluid dynamics as an emergent property from the interactions between very simple fluid particles.

5.1 Lattice gas methods

Complete macroscopic hydrodynamic descriptions of complex fluids are often not known and, indeed, may not even exist. Therefore, a macroscopic approach in the form of continuum PDEs (essentially the Navier–Stokes equations with constitutive equations shoehorned in) are of doubtful validity. One might turn instead to a microscopic approach such as classical molecular dynamics (MD; see §6) but it is not yet possible to simulate bulk fluid over macroscopic time-intervals (at least seconds) using such techniques. Instead, we adopt a mesoscopic approach where the fluid behaviour emerges from the evolution of the simple rules that define the model. The basic elements of the two-dimensional model are simple to explain, yet their emergent behaviour is equivalent to that described by hydrodynamic equations for incompressible flows (i.e. the Navier–Stokes equations) when averaged over sufficiently large regions of space and long periods of time (Frish et al. 1986; Wolfram 1986).

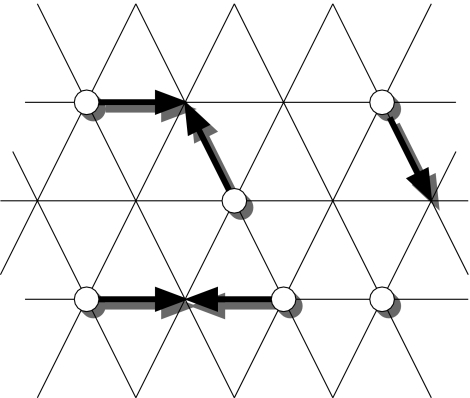
The fluid is represented by mesoscopic particles propagating and colliding on a regular lattice (figure 2). In this model, both space and time are discrete and therefore this is a kind of cellular automaton. The geometry of the lattice is chosen to guarantee isotropy of flow and in two dimensions, a triangular lattice is sufficient. In three dimensions, the geometry of the lattice is rather more complicated (a projected four-dimensional hypercube). The particles are Boolean, i.e. they can only be present or absent from a given velocity vector at a lattice site, as is the dynamics. In terms of the atomic theory of matter, it is not clear what a single mesoscopic particle of fluid represents; they are simply chosen to give the correct macroscopic fluid behaviour with each tick of the automaton clock. The mesoscopic particles propagate by a single lattice spacing at each tick and then collide conserving mass and momentum. It is these collision laws that are ultimately responsible for the correct hydrodynamic behaviour. The particles are propagated again and the entire process repeats leading to physically realistic, incompressible, single-phase flow on the macroscopic scale (i.e. for lengths and times much larger than the intrinsic lattice space and time-scales).

Figure 2.

Simple two-dimensional lattice gas dynamics.

Lattice gas models provide excellent examples of our earlier definition of complexity. The collision rules ensure that these systems are irreversible and nonlinear leading to the emergence of complex, self-organizing phenomena. Multicomponent fluids provide particularly clear examples of these, for example, in the separation of two immiscible phases. The lattice gas automaton connects the descriptions of the particles at a shorter length-scale to emergent behaviour at a longer length-scale. Finally, although the rules of the model are simple to understand, a computer is required to perform the simulations, to visualize and analyse the results and to store the data. In two dimensions, this can be a workstation, but in three dimensions, one generally requires a parallel computer in order to perform any serious investigation.

As indicated above, lattice gas models have been extended to mixtures of two immiscible fluids, with (ternary fluid) or without (binary fluid) an amphiphile. A binary model was first introduced by Rothman & Keller (1988) by adapting ideas from electrostatics. Mesoscopic particles from different species are assigned different colour ‘charges’ (conventionally blue for water and red for oil). An order parameter is defined at each lattice site, as the difference in the colour densities of the two fluids. Phase separation is achieved by choosing a post-collisional order parameter flux for which its work against the colour field, a vector field defined by the order parameter at surrounding lattice sites, is minimized, or preferentially selected by some kind of Monte Carlo procedure. This model reproduces spinodal decomposition (the separation of immiscible fluids) and has been further extended to include surfactants (Boghosian et al. 1996).

Lattice gas models describe the flow of complex fluids well; they give the correct hydrodynamics, immiscibility, interfacial and self-assembly behaviours for low Reynolds numbers (Love et al. 2001; Love & Coveney 2002). They are comparatively simple to understand and implement and, given the Boolean nature of the rules employed, are computationally unconditionally stable, which is a very attractive feature as far as their numerical simulation is concerned. The discrete nature of the mesoscopic particles also leads to significant fluctuations, which are vital to model certain physical phenomena but can sometimes make it difficult to observe standard hydrodynamic phenomena without extensive ensemble averaging (Chen et al. 2000).

5.2 Lattice-Boltzmann methods

Lattice-Boltzmann models are rather more recent (Succi 2001) and overcome many of the problems listed above that afflict lattice gases. The lattice particles are discarded and each velocity at each lattice site is instead populated with a single-particle probability distribution function, which relaxes towards a tailored, predefined Maxwellian equilibrium state. As with their lattice gas progenitors, these models conserve mass and momentum throughout, but they are susceptible to machine-precision errors resulting from their use of floating-point arithmetic. There are no fluctuations, unlike the lattice gas case, and the models are algorithmically much simpler to implement. However, they are not unconditionally stable owing to the lack in general of an ‘H-theorem’ guaranteeing the existence of a Lyapunov function H (the H-function is the negative of Boltzmann's entropy), which evolves in a monotonically increasing manner to its minimum at equilibrium (Boltzmann 1886; Coveney & Highfield 1991). Notwithstanding their drawbacks, lattice-Boltzmann schemes are widely used and several exist for the study of multicomponent and amphiphilic fluids.

Entropic lattice-Boltzmann models by contrast do not have an arbitrary equilibrium distribution function towards which the single-particle distribution functions relax. Instead, an entropy (or H-) function is defined, which, by construction, can only increase in magnitude as the model evolves. For incompressible flow, it has been shown that requiring the models to be Galilean invariant essentially fixes the H-function (Boghosian et al. 2003). Such models are unconditionally stable and permit the fluid viscosity to assume vanishingly small values—which is of considerable value in studying turbulence, still a grand challenge problem in classical physics.

Both lattice gas and lattice-Boltzmann models are very different to the more conventional networks of nonlinear coupled differential equations used to describe the behaviour of the heart and circadian rhythms in §4. However, both approaches rely on simple units (mesoscopic particles of fluid or cells or proteins and other molecules) interacting to reproduce the behaviour of interest. The simplicity of the lattice-Boltzmann and lattice gas models indicates that fluid dynamics primarily emerges from the interactions between the units rather than from the properties of the units themselves. In biological systems, the units (e.g. proteins) tend to be intrinsically very complicated and, consequently, such alluringly simple theoretical models cannot easily be constructed while retaining the interest of bona fide biologists. We will discuss reasons for this in the context of biomolecular modelling in §6.

6. Biomolecular modelling and computational systems biology

Understanding and predicting the properties and behaviour of biomolecules (e.g. proteins and nucleic acids) is an important and highly active area of research in molecular biology, biochemistry and chemical biology. Beyond investigating many important biological phenomena (e.g. antibiotic drug resistance), models of biomolecular systems are expected to form part of (hierarchical or hybrid) multiscale approaches with the advantages already discussed. Within this discipline, hybrid multiscale models already exist that combine quantum and classical mechanics (QM/MM) to study, for example, enzymatic reactions (Leach 2001), but these are rather ad hoc at present.

Biomolecular models are usually atomistic and based on classical MD, because the degree to which it is possible to coarse-grain a biomolecular system (while retaining a good representation of biological behaviour) is limited. Ab initio MD is out of the question owing to the computational cost. Even classical molecular models require enormous quantities of computational power, although a hybrid multiscale approach may mitigate this to some degree by only applying an atomistic description to those parts of a biomolecular system where it is necessary.

In this section, we shall first briefly consider the tension between practitioners of deductive and inductive modelling before discussing why an atomistic description must be retained. Finally, we shall examine a more detailed example of a hybrid multiscale model, HybridMD, particularly the algorithm that maintains the interface between the two descriptions. The general same principle is applicable throughout systems biology and may, as alluded to earlier, form one layer within a true hybrid matryoshka multiscale model for the study of, for example, the electromechanical behaviour of the mammalian heart.

The tension between Popperian and Baconian approaches within the biological sciences is most keenly felt in the domain of biomolecular modelling, especially in the highly competitive field concerned with protein structure prediction, for example, the critical assessment of techniques for protein structure prediction experiments (http://predictioncenter.llnl.gov/). This is a shame because, although comparisons are often made (e.g. Schonbrun et al. 2002), it is plainly nonsensical to compare protein structure predictions made by bioinformatics (an inductive approach) with ensembles of structures produced by MD (a deductive approach), because the former usually yields a static snapshot of the protein's structure typically frozen at 100 K, whereas the latter gives a dynamic view of the protein's structure at physiological temperatures. Instead, we should recognize that these approaches are complementary.

The free energy change between an initial disordered state and the final structure of a protein (the process known as folding) is typically very small, of the order of a few hydrogen bonds (5–15 kcal mol⁻¹; Dobson et al. 1998). This is the result of the similar magnitudes of the enthalpic and entropic components of folding. This delicate balance has frustrated all attempts to coarse-grain the description of a protein beyond classical MD, an approach that computes the forces acting on each atom using a force field, such as Charmm or Amber (Pearlman et al. 1995; MacKerell et al. 1998). The time-step by which the integrator can be advanced is constrained to only a few femtoseconds by the fastest oscillation within the system (Leach 2001; Frenkel & Smit 2002). This places most phenomena out of the reach of classical MD, although in the last 10 years, improvements in the treatment of electrostatics and the development of scalable parallel codes has begun to bring significant improvements. Nonetheless, a solvated system comprising a single major histocompatibility complex protein, an epitope (a short peptide) and a T-cell receptor protein contains around 100 000 atoms and requires tens of thousands of central processing unit (CPU) hours on a supercomputer to simulate 10 ns of dynamics (see the studies by Wan et al. 2004, 2005). The study of biomolecular systems using classical MD clearly necessitates the use of high-performance computing (HPC), and this has been recognized by the development of a new generation of fast, scalable MD codes, for example, GROMACS (Berendsen et al. 1995) and NAMD (Kalé 1999). NAMD has been recently awarded a Gold Star award at HPCx, a UK supercomputer, for its ability to scale well up to 1024 processors when simulating sufficiently large systems.

Even a comparatively complicated biomolecular system of the kind described above is around 65% water and therefore not only is the majority of the computational effort spent computing forces between water molecules, but the finite size of the system can also introduce unphysical effects. Consequently, modelling the bulk of the water using a simpler, continuum-based description while retaining an atomistic description (such as classical MD) for the protein and surrounding water would remove the finite size effects and reduce the computational overhead considerably. This is a hybrid multiscale model and the main challenge is constructing the interface between the continuum and molecular domains. Water must be able to flow from one region to the other; however, it is not immediately obvious how to transmute a flux from the continuum region into the molecular domain and also conserve mass, momentum and energy. Developing efficient particle insertion algorithms is an active area of research of direct relevance to this approach (see Delgado-Buscalioni & Coveney 2003b and references therein). We shall briefly describe one such algorithm, USHER, as developed by Delgado-Buscalioni & Coveney (2003a,b), its inclusion in a simple model, HybridMD, and its application to a simple system (Barsky et al. 2004).

Consider a basic model of the behaviour of DNA tethered to a wall in shear flow (Doyle et al. 2000). The DNA is represented by a simple polymer composed of beads, the last of which is tethered to a wall (also composed of beads) and solvated by a van der Waals liquid up to a certain height. Above this interface, the liquid is represented by a continuum regime, the solvent is sheared in a direction parallel to the wall by applying a shear boundary condition in the continuum regime and the dynamics followed using a CFD solver. An equivalent, but entirely particulate, MD simulation is also performed for comparison purposes.

The flow of mass, momentum and energy fluxes across the interface requires the insertion of particles and the alteration of flows in the particulate and continuum regions respectively. USHER handles the more difficult of these two cases; that of inserting particles into dense fluids at a site where the potential energy takes exactly the desired value. It does so not by explicitly searching for cavities within the solvent but rather by a combination of (i) randomly selecting a starting site and (ii) applying a steepest descent algorithm whose displacement step is dynamically adapted according to the local topology of the energy landscape. For more detail, the reader is referred to the study by Delgado-Buscalioni & Coveney (2003b).

The HybridMD model reproduces the behaviour of the MD model but the computational cost of the insertion procedure is only 6% of that of the MD algorithm (Barsky et al. 2004). This is an encouraging result and we look forward to applications of this and similar methods to biomolecular systems. Indeed, the USHER algorithm has recently been extended to handle the insertion of polar molecules (notably water) into dense liquids (De Fabritiis et al. 2004). Water is particularly challenging because of its propensity to form extensive hydrogen bonded networks with its neighbours, including proteins (Levy & Onuchic 2004). This substantially reduces the number of insertion sites with low potential energy compared to, for example, a simple van der Waals liquid. Treating water correctly is an essential step in the simulation of biological systems using hybrid models of this kind as well as providing a route to the modelling and simulation of open systems. We emphasize that a simple increase in the speed of simulations and the removal of finite size effects are not the only advantages, but are merely the first benefits to be displayed.

A further challenge is the development of new or existing algorithms to be used within a hybrid model. The ability to replace one CFD solver by another, or perhaps a different algorithm entirely, as well as to ‘plug and play’ a variety of different MD codes is necessary to make such hybrid multiscale codes widely applicable and attractive to large numbers of scientists (Delgado-Buscalioni et al. in press; Mayes et al. in press). This, in addition to the running the different component codes on different computers for efficiency reasons, will be discussed in the §7.

7. Grid computing

An integrative approach to studying biological systems, especially if biomolecular detail is included, requires extensive computational resources of all forms for calculation, visualization and data storage. The (potentially multiscale) models that comprise such an approach are usually deductive in nature, but an inductive modelling approach (such as that taken by bioinformatics) also requires substantial computational resources to process, store and retrieve the vast quantities of genomic and other kinds of data that are accumulated. The growth of computational systems biology has often been constrained by a lack of adequate computational resources; the advent of computational grids offers one method of addressing this problem. For more information on computational grids, see the reviews by Foster & Kesselman (1999), Foster et al. (2001), Berman et al. (2003), Foster & Kessleman (2003), Taylor (2004) and the URLs printed later in this section. Additionally, a set of papers discussing in more detail many of the concepts introduced within this section can be found in a forthcoming publication, Scientific grid computing (Coveney in press).

The concept of a ‘computational grid’ has been mentioned in passing and its potential has been alluded to, so we should now define what it is. Grid computing is distributed computing performed transparently across multiple administrative domains; transparency implies that there is minimal complexity for the user. Here, computing refers to any form of digital activity, not just numerical computation.

The term ‘computational grid’ was coined in analogy with the electricity grid that seamlessly supplies electrical power to our homes, offices and industry (Vyssotsky et al. 1965; Foster & Kesselman 1999). When we switch a kettle on to make a cup of tea, we do not know, nor do we need to know, the source of the electricity that is heating the water—we just plug our appliances into the power sockets and pay the bills. The vision for a computational grid is similar; it would securely, seamlessly and transparently supply us with computational resources (number crunching, visualization, database access, data storage, etc.) on demand. All we would have to do is pay the bill and hence computing would have become a commodity. This would represent a genuine paradigm shift in both how we use computers to further scientific knowledge and, indeed as humans, how we collaborate. Properly fulfilled, the vision of grid computing would benefit all of science and society (Coveney 2003b) but, as we shall discuss later, we are currently still some distance from realizing this goal.

Data sources, in the form of instruments, may also be attached to a computational grid. Indeed, it is the approaching commissioning of the Large Hadron Collider in 2007—and the required analysis and storage of the petabytes of data that it will generate—that has provided much of the initial impetus for the development of this technology. The size and scale of this project, however, is also a risk to the successful development of grid computing as too much focus on the needs of experimental high-energy physics (particularly its more or less exclusive emphasis on running a large number of independent jobs each on single CPUs of loosely coupled compute clusters—so-called ‘task-farming’) might inhibit the needs of other forms of grid computing being properly addressed.

There has been a growth in the number of research projects that aim both to develop the infrastructure necessary for computational grids and to solve scientific problems by deploying models on them, particularly within the current 5 year UK e-Science programme (2001–06). We note that many UK e-Science projects are Baconian in nature and are therefore primarily concerned with data processing and inferential models (Berman et al. 2003). This distortion presents a second risk to the balanced development of grid computing. It is vital for scientists to be involved at an early stage in the development of grid infrastructure in order to convey their requirements to the computer scientists and software engineers developing computational grids.

7.1 Computational steering and grid-based workflows

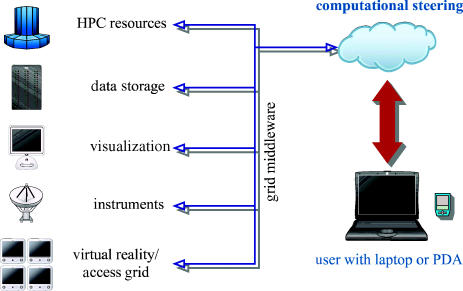
P.V.C. is the principal investigator on a major UK e-Science project called ‘RealityGrid’ (www.realitygrid.org), which is concerned with pioneering the performance of real computational science on grids. RealityGrid (figure 3) has developed and continues to develop tools to allow the seamless and transparent deployment of a variety of condensed matter models on computational grids from physics and chemistry to materials and biology.

Figure 3.

A schematic of the UK e-Science RealityGrid program demonstrating the different computational resources used and the centrality of computational steering.

A central tool developed by RealityGrid is the steering library, an application programming interface (API) available for download (Pickles et al. in press). Once a scientific application has been interfaced with the RealityGrid steering library API, the scientist is able to monitor and interact with the simulation (i.e. to steer it) in a wide variety of ways. All communication is carried out via a central registry and therefore, in principle, the scientist does not have to know where the simulation is running. Several existing scientific codes have already been interfaced with the steering library (Pickles et al. in press), including a lattice-Boltzmann code (Harting et al. 2004) and NAMD (Kalé 1999), one of our chosen classical MD production codes, with the aim of significantly extending our capacity to do computational science using HPC.

Applying the concept of computational steering (Chin et al. 2003) along with the real-time visualization of a simulation allows one or more computational scientists to interact with a simulation or set of simulations to ensure that the maximum understanding is gained using the minimum of computational resource and elapsed wallclock time. Consider the current process of using a high-performance computer. Here, the computational scientist prepares a set of input files and therefore must make important decisions about various aspects of the simulation before run-time, for example, how long it will run for. These files are then submitted to a specific high-performance computer where the code to be used has been previously compiled and a job is submitted to the batch queue. There is little or no interaction with the simulation while it progresses. The scientist then recovers the data output by the simulation, analyses it and, if he or she is lucky, there may be some interesting data. Computational steering aims to recast this process by allowing the scientist to interact in near real time with many simulations as they progress. Monitoring the separation of two immiscible fluids and adjusting a coupling parameter to achieve the desired behaviour is one example (Harting et al. 2004).

The steering library further allows simulations to take checkpoints and for those checkpoints to be moved onto another computer, perhaps with a different architecture, and then used to start a new simulation. This important feature is called malleable checkpointing (Mayes et al. in press) and allows scientists to clone or spawn simulations to, for example, explore several different parameter values before back-tracking to the checkpoint and proceeding with the chosen value. The ability of simulations to take checkpoints also allows more complicated grid workflows to be constructed. At the very least, steering and checkpointing can prevent computational cycles being wasted by needless simulation. Used judiciously, it can lead to new science that would have been impractical using the old ‘fire-and-forget’ mode of working.

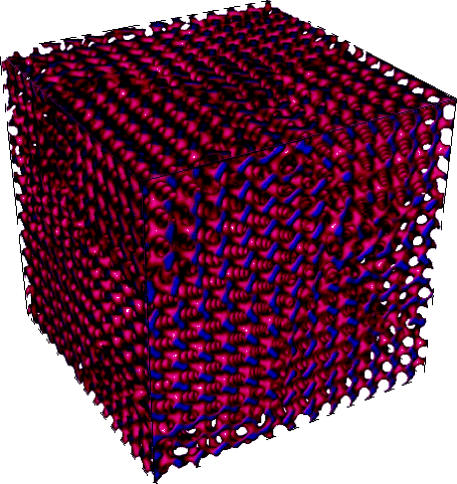
RealityGrid has run two successful large-scale computational projects federating the US and UK computational grids that made extensive use of steering. The first, TeraGyroid, investigated an exotic cubic liquid crystalline amphiphilic fluid mesophase, the beautiful gyroid phase; see figure 4 (González-Segredo & Coveney 2004a,b). Interestingly, some scientists believe that the endoplasmic reticulum is gyroidal in structure (Landh 1995). During the TeraGyroid Project, we ran the largest set of lattice-Boltzmann simulations to date using our home-grown LB3D code within a study of defect dynamics. The work tied together more than 6000 processors and 17 teraflops of computing at six different facilities on two continents, including high-end visualization machines, by federating the US TeraGrid with the UK's supercomputing facilities at HPCx and CSAR and a visualization engine at UCL.

Figure 4.

A gyroid phase displaying defect dynamics (as modelled by a three-dimensional lattice-Boltzmann code).

This project won the HPC Challenge Award for most data-intensive application at Supercomputing 2003 in Phoenix, Arizona, USA and an integrated data and information management award at the International Supercomputing Conference in Heidelberg, Germany, 2004. For more information, the reader is referred to papers by Harting et al. (2003), Chin et al. (2004), Pickles et al. (2004), Blake et al. (in press) and Haines et al. (in press).

A more recent project undertaken by Fowler et al. (2004) aimed to calculate a difference in binding affinities between two peptides and an Src SH2 protein domain in under 48 h during the course of the 2004 UK e-Science All Hands Meeting at the University of Nottingham. The calculation of such quantities is of vital importance, both academically and to the pharmaceutical industry, because a successful computation can yield significant insight into how a drug candidate binds to its target. The technique, thermodynamic integration (Pearlman & Rao 1999; Leach 2001), is well established, but its widespread adoption is hampered by its extreme complexity and very high compute intensity (Chipot & Pearlman 2002). As part of this project, the MD code NAMD was interfaced with the RealityGrid steering library. This allowed the launching, control, spawning and steering of the many classical MD simulations required to compute a single difference in binding affinities. This process is referred to as steered thermodynamic integration using molecular dynamics; for more details see Fowler et al. (in press).

7.2 Towards a general coupling framework for hybrid multiscale models

As mentioned in §3.2, another RealityGrid research activity is the development of a coupling framework that manages both the coupling of codes (e.g. CFD and MD) and their subsequent deployment on a range of computer architectures, from single workstations (where each model must execute in sequence) to parallel computers and computational grids. A bespoke version of the HybridMD model discussed earlier is being developed, which should be deployable in this flexible fashion (Delgado-Buscalioni et al. in press). Within this framework, XML-based metadata must be included to describe the individual models being coupled, their composition within the coupled system and their deployment on specific resources. Consequently, this metadata has a different and more complicated function to that of the Systems Biology Markup Language.

A ‘bespoke framework generator’ produces the appropriate control and communication code enabling the model to be coupled in the specified manner. Several benefits are apparent, including (i) individual models can be composed into the coupled system using composition metadata with no change to the model code and (ii) code can be generated to run a particular coupled model on a specified architecture (e.g. personal digital assistant PDA, desktop, parallel machine or a computational grid) simply by changing the metadata. This approach to coupled models is at a very early stage of development; we ourselves are looking at other frameworks that may be more flexible (Coveney et al. 2004).

For the computers involved to interface with one another and with the RealityGrid bespoke job control software, some kind of ‘middleware’ has to be adopted. Globus (www.globus.org) is the current de facto middleware and, as such, is installed on most of the resources that claim to be ‘grid-enabled’—the US Teragrid (www.teragrid.org), the UK National Grid Service (www.ngs.ac.uk) and the European grid produced by the Enabling Grids for E-SciencE programme (Gagliardi et al. (in press; egee-intranet.web.cern.ch). Globus is not on its own a complete solution (Chin & Coveney 2004), and RealityGrid also uses the Perl grid middleware packages OGSI:Lite and WSRF:Lite (based on two different grid specifications) to provide essential additional services required for any scientific application (McKeown 2004).

7.3 The present state of computational grids

It would be misleading to give the impression that today's computational grids are well developed and easy to use. In fact, it is extremely difficult to set up such grid projects as they require both extensive support by dedicated software engineers and for all concerned to climb a steep learning curve (Chin et al. 2004). This current lack of usability has several sources: (i) there is lack of a common API for core functionalities (e.g. file transfer) usable across distinct grid applications and domains. Consequently, the application developer (who most often is also the end-user scientist) is left with no option but to hard code domain specific, grid-level calls into the given application; (ii) heterogeneous software stacks make grid-application portability a nightmare; (iii) there is a high barrier for getting security certificates accepted beyond the issuing domain; (iv) scheduling and job launching resources and policies are frequently non-uniform and incompatible and (v) as we have highlighted extensively (Chin & Coveney 2004; Coveney et al. 2004), much existing grid middleware is difficult to use and is detrimental to most scientific research, in flagrant violation of the stipulated goal of grid computing which is meant to be ‘transparent’ for users.

Notwithstanding the current problems for users of grid computing, we believe that, if present efforts are sustained—for example through the efforts of the UK's Open Middleware Infrastructure Institute (www.omii.ac.uk), albeit with more attention being paid to users' needs—grid computing should become of significant value to many computational scientists, including those working in computational systems biology, in the next 3–5 years.

8. Complex biological networks, universality and the origin of the RNA world

Biochemical pathways and networks are, in their full glory, of immense complexity and correspond mathematically to very high-dimensional sets of coupled nonlinear ordinary or PDEs; the reader is referred back to the discussion of models of circadian rhythms in §4 for an example. These equations contain a very large number of parameters, which must generally be determined empirically. Typically, they are rate coefficients for various molecular processes. From a theoretical standpoint, it would be very helpful if one could demonstrate that certain quantitative macroscopic behaviours were insensitive to the details of many of the individual coefficients; that is, that it would not be necessary to know all these parameters. We have shown this to be the case for certain complex kinetic schemes based on the Becker–Döring model for stepwise polymerization/depolymerization as shown below

$$C_r+C_1\rightleftharpoons C_{r+1}.$$ (8.1)

More generally, they represent a wide range of nucleation and growth systems (Coveney & Wattis 1999; Wattis & Coveney 2001a,b). For the Becker–Döring process given in equation (8.1), we can write down the kinetic equations for the formation of RNA sequences

$${\dot{c}}_r=J_{r-1}-J_r,r=2,3\dots ,$$ (8.2)

$${\dot{c}}_1=-J_1-\sum _{r=1}^{\infty }{J}_r,$$ (8.3)

$$J_r:=a_r{a}_r{c}_1-b_{r+1}{c}_{r+1}.$$ (8.4)

Here, c_r is an RNA sequence of length r with the dots representing the time derivatives. J_r represents the flux of sequences growing by a single monomer from sequence c_r to c_r+1 and a_r is the forward rate coefficient from equation (8.1) and b_r+1 the backward rate coefficient. Equations (8.2)–(8.4) are an infinite set of coupled nonlinear ODEs; to solve the equations, we need to know two times an infinite number of rate coefficients. It is possible to systematically coarse-grain these equations by a renormalization group transformation to a set of low-dimensional (two- or three-dimensional) nonlinear ODEs whose dynamics can be solved by standard phase–plane methods. The nub of the method is that the renormalization group analysis of the infinite set of nonlinear ODEs shows that the dynamics, at the macroscopic level, subdivides into only a few ‘universality classes’, and hence it is not necessary to know all the microscopic rate coefficients to determine the long-time (asymptotic) dynamics (Coveney & Wattis 1999; Wattis & Coveney 2001a,b). Theoretical approaches along these lines would allow the precise determination of the rate coefficients, or properties of rate coefficients, of complex biochemical networks that need to be measured in order to predict the asymptotic behaviour of a biological system.

As an illustration of the power of such a contraction procedure, consider the evolution of RNA sequences of differing lengths from an initial mixture of RNA monomers. Unlike proteins and DNA, an RNA molecule can both store genetic information and catalyse chemical reactions, as shown by Altman and Cech who won the 1989 Nobel Prize in chemistry (Zubay 2000). The hypothesis that RNA sequences spontaneously evolved from a Darwinian primordial soup to produce the earliest forms of life on Earth is known as the RNA world view (Zubay 2000). How life originally evolved can therefore be divided into two questions: (i) Where did the RNA world come from? and (ii) How did this RNA world evolve into the current molecular biology dogma that DNA makes RNA makes protein? The study by Wattis & Coveney (1999) concentrates on the first question, which may itself be further subdivided: How did RNA ‘monomers’ of the correct chirality arise (Wattis & Coveney in press) and how did they interact to produce a rich RNA-polymer based system?

Given that the maximum possible sequence length of RNA polymers is unbounded, the set of Becker–Döring (nonlinear ordinary differential) equations that describe the origin and evolution of the RNA polymers is infinite. This set of equations is coarse-grained, as described above by considering only monomers, short chains and long chains and the resultant low-dimensional set of equations reproduces the desired behaviours (Wattis & Coveney 1999). Hydrolysis prevents the formation of RNA polymer sequences of infinite length while still permitting the accumulation of longer RNA polymers. The same study by Wattis & Coveney (1999) demonstrated that viable concentrations of RNA chains of sufficient length will form after sufficient time if the appropriate catalytic and hydrolysis mechanisms are present. This is a clear illustration of the utility of a complexity-led approach, which, in this case, is predominantly analytical.

9. Conclusion

Like the physical sciences, the biological sciences are recognizing the need to embrace the integrationist approach and therefore the concept of complexity. This is most clearly seen in the rapid growth of systems biology, which typically describes systems such as the dynamics of the heart or circadian rhythms using nonlinear coupled differential equations. Although sometimes described as molecular, such models do not explicitly include atomistic detail permitting the modelling of the dynamics of individual biomolecules (e.g. ion channels). To do so would allow the calculation of unknown coefficients within the existing differential equation-based models and excitingly would permit the study of how minute changes at the biomolecular level influence, for example, the electrophysiological properties of the heart. Such changes include genetic mutations, or the presence or absence of small molecules such as drugs.

Combining both models would yield a multiscale model and would be a first step towards connecting behaviours at different length- and time-scales, thereby integrating different biological disciplines. Although there is discussion of multiscale models in, for example, the Physiome Project, these are hierarchical and consequently avoid many of the problems by limiting the communication between the component models. To include atomistic detail will probably require the construction of true hybrid, coupled multiscale models. These are far more complicated to build, primarily owing to the problem of dynamically interfacing the two algorithms. HybridMD (and its attendant particle insertion algorithm USHER) is an example of an embryonic hybrid model that could be further incorporated within the conventional systems biology models with the advantages already discussed.

Biological systems are intricate and complicated. This is apparent in how biomolecular models cannot be coarse-grained in the same gross way that lattice gas and lattice-Boltzmann models have been. At the same time, the biological sciences differ fundamentally from the physical sciences today in their more balanced use of both deductive and inductive approaches to modelling. We must ensure that ideological differences do not prevent practitioners of these different approaches working together to produce new science.

Theory can provide a means of analysing and simplifying a set of coupled nonlinear differential equations, as shown by the renormalization method for contracting sets of Becker–Döring equations. The application of this method to the evolution of RNA polymers was briefly described and we hope and expect that theoretical developments along these lines continue.

Finally, many of these modelling techniques require growing amounts of computational resource. If their potential is realized, then computational grids will provide a deluge of computational resource and will enable us, as computational scientists, to exploit these resources in more imaginative ways than is currently possible. For example, the different components of a multiscale model could be deployed on different computers in different geographical locations although, as scientists, we would be blissfully oblivious to this. Within the UK e-Science project, RealityGrid, we have already taken important steps to change the manner in which we run simulations through the use of advanced forms of computational steering.

The improvements in theory, techniques and the quantity of computational resource becoming available make us optimistic that significant progress can be made in applying integrationist approaches in biology, thereby promoting a deeper understanding of the exquisite organization and complexity of life itself.