Skip to main content
NCBI home page
Journal of the Royal Society Interface logoLink to Journal of the Royal Society Interface
. 2005 May 10;2(3):159–167. doi: 10.1098/rsif.2005.0035

Age-dependent residual tensile strains are present in the dura mater of rats

James H Henderson 1,2,†, Randall P Nacamuli 3, Betty Zhao 1, Michael T Longaker 3, Dennis R Carter 1,2
PMCID: PMC1629075  PMID: 16849176

Abstract

The objectives of this study were to determine whether residual tensile strains exist in the dura mater of mammals in vivo, and whether the strains are age-dependent. We made incisions in the parietal dura mater of immature and mature rats, and measured the retraction of the dura mater from each incision. We then used a finite-element model to calculate the strain present in the parietal dura mater of each rat. We found that age-dependent residual tensile strains are present in the dura mater of rats. The mean average residual strain of the immature rats was significantly larger than that of the mature rats (4.96±1.54% (s.d.) versus 0.39±0.13%, p<0.0001), with the mean strain calculated in the mature rats of the order of the minimum measurement that could be made using our experimental approach. In addition, in the immature rats mean residual strain in the longitudinal direction was significantly larger than mean residual strain in the transverse direction (6.11±3.62% versus 3.82±2.64%, p=0.0218). Our findings show that age-dependent residual tensile strains exist in the dura mater of rats. We speculate that these strains may reflect the rate and direction of cranial growth and may also influence cranial healing.

Keywords: calvarial healing, mechanobiology, cranial growth and development, growth-generated strain, prestress

1. Introduction

Both the human cranium and the rat cranium grow rapidly during early postnatal development, as approximately 90% of intracranial volume growth has occurred by two years of age in humans and by two months of age in rats (Abbott et al. 2000; Fong et al. 2003; Henderson et al. 2004b). Growth during development can generate residual strains and stresses (or prestresses) in connected tissues that grow at different rates (Henderson & Carter 2002). Residual strains and stresses are the strains and stresses that remain in a tissue or organ after all external loads have been removed (Gregersen et al. 2000).

Residual strains and stresses have previously been found in the tissues of a number of organ systems, including the cardiovascular system (Vaishnav & Vossoughi 1983; Fung 1984; Han & Fung 1996; Vaishnav & Vossoughi 1987), the gastrointestinal tract (Gregersen et al. 2000) and the musculoskeletal system (Bertram et al. 1998; Popowics et al. 2002). It has been proposed that residual strains and stresses may influence not only the biomechanical behaviour of tissues, but also the local cell biology of the tissues (Gregersen et al. 2000). For example, in the duodenum of the gastrointestinal tract, the prestress owing to residual strain may contribute to increased resistance to luminal pressures (Gregersen et al. 2000). In addition, the residual strains may influence local cell biology and thereby influence the height of the mucosal villi (Gregersen et al. 2000). In the perichondrium/periosteum of developing bones, the prestress owing to residual strain may play a structural role in some locations, such as the zygomatic arch (Popowics et al. 2002). In addition, the residual strains may influence the growth of the associated bones (Warrell & Taylor 1979; Bertram et al. 1998; Popowics et al. 2002).

The objectives of this study were to determine whether residual tensile strains are present in the dura mater of mammals in vivo, and whether the residual tensile strains are age-dependent. To achieve these objectives, we harvested the calvariae of immature and mature rats, made incisions in the parietal dura mater and measured the retraction of the dura mater from the incisions. Using a finite-element model, we then calculated the residual tensile strain present in the parietal dura mater of each rat.

2. Methods

2.1 Animals

Time-dated Sprague–Dawley rats were purchased from Charles River, Inc. (Wilmington, MA). All rats were housed in a temperature- and light-controlled environment and provided with food and water ad libitum. All experiments were performed in accordance with Animal Care and Use Guidelines for Stanford University.

2.2 Calvarial harvest and dural incision

A total of 34 immature rats were euthanized via CO2 asphyxiation at the following ages: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24 and 26 postnatal days (n=1–4 rats per age group). An additional seven mature rats were sacrificed between 95 and 105 postnatal days. Calvariae were carefully dissected free (leaving intact the dura mater underlying and attached to the frontal, parietal and occipital bones), and were washed in phosphate-buffered saline (PBS). Great care was taken to maintain the dural attachments at the borders of the parietal bone, specifically the coronal suture (anterior border), sagittal suture (medial border), occipital suture (posterior border) and sphenoparietal suture (lateral border), as these sutural attachments of the dura mater to the cranium maintained the dura mater in a strained state after the calvaria was dissected free of the surrounding tissues.

Surgical incision of the dura mater was performed under a dissecting microscope with the calvariae immersed in PBS. A longitudinal (anterior–posterior) incision was made with a No. 15 blade scalpel in the dura mater over the flattest part of one of the parietal bones (figure 1); the anatomical side of the longitudinal incision was randomized for each rat. A separate transverse (medial–lateral) incision was then made perpendicular to the first incision in the dura mater over the contralateral parietal bone. For each rat, the length of each incision was made in approximate proportion to the size of the cranium. As such, the length of the incisions tended to increase with the age of the rat.

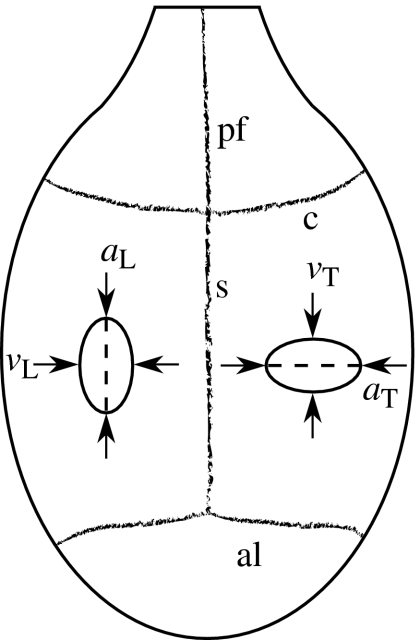
Figure 1.

Figure 1

Open in a new tab

Schematic of the rat cranial vault, showing the approximate location of the longitudinal and transverse incisions. This dorsal view shows the posterior frontal (pf), sagittal (s), coronal (c) and anterior lambdoidal (al) sutures. The anterior–posterior and medial–lateral dashed lines indicate the approximate locations at which the respective longitudinal and transverse incisions were made in the dura mater. The anatomical side of the incisions was randomized for each rat. The solid ovals illustrate how the edges of the incision often retracted, causing the incision to assume an elliptical shape. The length (a) and maximum width (v) of each incision was measured as shown.

Following incision, the dura mater was allowed to relax for 5 min to permit the tissue to reach a new equilibrium state. During incision or the subsequent relaxation period, the edges of the incision often retracted, causing the incision to assume an elliptical shape (figures 1 and 2a). Images of the incisions were then captured at a minimum resolution of 1600×1200 pixels using a Nikon Coolpix 5700 digital camera (Nikon; Melville, NY) attached to the dissecting microscope. Image dimensions were calibrated to a known standard and the length (a) and maximum width (v) of each incision was measured by a single trained operator using ImageJ software (NIH; Bethesda, MD; figures 1 and 2a). For each length or width measured, two independent measurements were made and then averaged. There was a relatively low difference between the two measurements, with an average absolute difference of 5.65% for all immature measurements and 11.96% for all mature measurements.

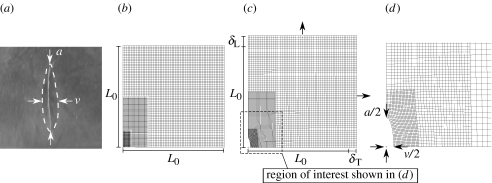
Figure 2.

Figure 2

Open in a new tab

A longitudinal incision in the dura mater of a 2-day-old rat and the finite-element model used to calculate the strains present in the dura mater. (a) Following incision, the length (a) and maximum width (v) of each incision was measured. The dashed line denotes the edge of the incision after being allowed to relax for 5 min. (b) The finite-element model used to calculate retraction of the edges of an incision made in rat dura mater under varying levels of tensile strain. The unstrained model had an initial side length of L0. (c) Longitudinal (δL) and transverse (δT) displacements were applied to the edges of the model to simulate straining of the dura mater in both the longitudinal and transverse directions. (d) For each combination of δL and δT applied to the model, we recorded the half-length (a/2) and the maximum half-width (v/2) of the incision.

2.3 Calculation of residual tensile strain

A two-dimensional, plane stress, linear elastic, finite-element model with two axes of symmetry and nonlinear geometry was created to represent retraction of the edges of an incision made in rat dura mater under varying levels of simulated residual tensile strain (figure 2b). The initial side length of the unstrained model was L0=10 mm. The initial dimensions of the unstrained incision were 0.8333 mm long by 0 mm wide. Longitudinal (δL) and transverse (δT) displacements were applied to the edges of the model to simulate straining of the dura mater in both the longitudinal and transverse directions (figure 2c). The longitudinal (ϵL) and transverse (ϵT) strains applied by these displacements were calculated as ϵL=δL/L0 and ϵT=δT/L0. Analysis of the model was performed for 11 different magnitudes of δL (0–1 mm with increments chosen manually as 0.1 mm), with 11 magnitudes of δT (0 to ∼1 mm with increments chosen automatically during solution by the finite-element program (MSC.Patran, MSC.Software; Santa Ana, CA)) for each magnitude of δL, resulting in an analysis of a total of 121 combinations of δL and δT corresponding to 121 combinations of ϵL and ϵT. The maximum strain applied in either the longitudinal or transverse direction was therefore 10%. For each combination of δL and δT, and the associated ϵL and ϵT, applied to the model, we recorded the half-length (a/2) and the maximum half-width (v/2) of the incision (figure 2d). The assigned elastic modulus of the dura mater was 1 MPa (a parametric analysis showed that increasing or decreasing the elastic modulus by one order of magnitude had a negligible effect on the results; data not shown). The assigned Poisson's ratio of the dura mater was 0.45, based on previous finite-element modelling of human dura mater (Voo et al. 1996). The closed-form Westergaard solution (Westergaard 1939) for the displacement of a through-thickness crack in an infinite plate loaded in biaxial tension was not used for this analysis, as the large displacements observed in the incised dura mater violated the small displacement assumption of the Westergaard solution. To accommodate the large displacements, the finite-element analysis was solved for nonlinear geometry. To verify the finite-element analysis results for small strains, the results were compared with the Westergaard solution results and, as expected, for small displacements, the finite-element results closely matched the Westergaard solution results (data not shown). For example, for a ratio of incision width to incision length (v/a) of 0.03553 mm mm−1, the Westergaard solution (0.976% strain) differed from the finite-element analysis solution (1.000% strain) by only 0.023% strain.

To calculate the residual tensile strains present in the parietal dura mater of each rat, we used the finite-element results to determine the mathematical relationship between the ratio of incision width to incision length (vL/aL) of a longitudinal incision made in dura mater under tensile strains of ϵL and ϵT. The equation describing this relationship was found by fitting a polynomial surface to the 121 values of vL/aL as a function of ϵL and ϵT that were produced by the finite-element analysis. To fit the polynomial surface, first a second-order polynomial was fit to the 11 values of vL/aL for which ϵT=0. Then, 11 first-order polynomials were fit to each set of values of vL/aL corresponding to a constant ϵL. A third-order polynomial was then fit to the slopes of the first-order polynomials. The equation for the polynomial surface was formed by combining the second and third-order polynomials. All polynomial fitting was performed in Excel (Microsoft; Redmond, WA). The polynomial surface closely fit the data: excluding the value of vL/aL produced by the combination of ϵL and ϵT closest to zero, the average absolute error between the value of vL/aL predicted by the polynomial surface and the value of vL/aL produced by the finite-element analysis was 0.29% (for the combination of ϵL and ϵT closest to zero, which was ϵL=0% and ϵT=0.01%, the error between the value of vL/aL=0.0005451 predicted by the polynomial surface and the value of vL/aL=0.0002470 produced by the finite-element analysis was 121%). The resulting equation for the polynomial surface,

vLaL=(−1.3225ϵL2+1.0966ϵL+0.0003)+ϵT(51.243ϵL3−3.5804ϵL3−2.2536ϵL+2.451), (2.1)

allows calculation of vL/aL for known values of ϵL and ϵT. To determine the corresponding equation for the ratio of incision width to incision length (vT/aT) of a transverse incision, we used the symmetry of the finite-element model and exchanged the longitudinal and transverse strain direction, which yielded

vTaT=(−1.3225ϵT2+1.0966ϵT+0.0003)+ϵL(51.243ϵT3−3.5804ϵT2−2.2536ϵT+2.451). (2.2)

The above equations allow calculation of vL/aL and vT/aT for known values of ϵL and ϵT. However, the present study required calculation of ϵL and ϵT from the known values of vL/aL and vT/aT measured in the dura mater of each rat. Therefore, for each rat, we determined the residual longitudinal and transverse tensile strains present in the dura mater from the measured incision dimensions (vL/aL, vT/aT) by simultaneously solving equations (2.1) and (2.2) for the combination of ϵL and ϵT that uniquely satisfied the two dependent equations. The Mathematica (Wolfram; Champaign, IL) software package was used for solution of the dependent equations. We then calculated the average residual strain (ϵAVG) in the dura mater of each rat as ϵAVG=(ϵL+ϵT)/2.

3. Results

We found that residual tensile strains are present in the dura mater of rats. As measured from the images of the incisions, the average longitudinal and transverse incision lengths were 3.24±1.22 mm (s.d.) and 2.95±0.78 mm for the immature rats and 5.31±0.98 and 4.04±0.79 mm for the mature rats. The increase in length of the incisions with the age of the rat resulted from each incision being made in approximate proportion to the size of the cranium. The average longitudinal and transverse incision widths were 0.44±0.17 and 0.55±0.27 mm for the immature rats and 0.05±0.02 and 0.07±0.03 mm for the mature rats.

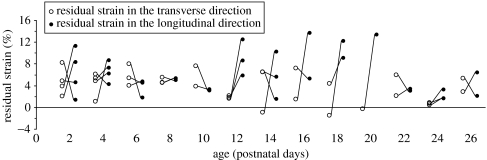
The mean average residual strain in the dura mater of immature rats was significantly larger than the mean average residual strain in the dura mater of mature rats (4.96±1.54% versus 0.39±0.13%, p < 0.0001; figure 3). Both means were significantly different than zero (p<0.0001 for immature rats and p=0.0002 for mature rats). However, the mean strain calculated in the mature rats is of the order of the minimum measurement that could be made (see §4), and indicates that the strains in the mature rats were too small to measure accurately using our experimental approach. Average residual strain (ϵAVG) in the immature rats (postnatal age 2–26 days) exhibited a weak but statistically significant decrease with age (r2=0.1827, p=0.0117; figure 4).

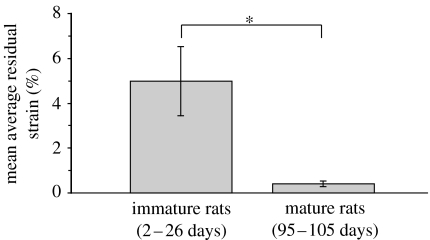
Figure 3.

Figure 3

Open in a new tab

Mean average residual strain in the dura mater of immature rats (postnatal age 2–26 days) versus mean average residual strain in the dura mater of mature rats (postnatal age 95–105 days). The mean average residual strain for immature rats was significantly larger than the mean average residual strain for the mature rats (4.96±1.54% versus 0.39±0.13%, p<0.0001). However, the mean strain calculated in the mature rats is of the order of the minimum measurement that could be made (see §4), and indicates that the strains in the mature rats were too small to measure accurately using our experimental approach.

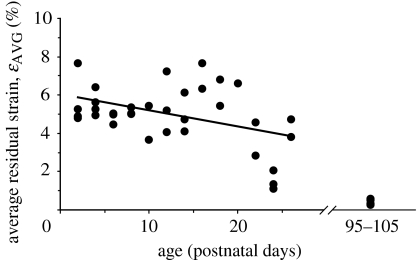
Figure 4.

Figure 4

Open in a new tab

Average residual tensile strain versus age in the dura mater of immature and mature rats. The average residual strain (ϵAVG) in the immature rats (postnatal age 2–26 days) exhibited a weak but statistically significant linear decrease with age (ϵAVG=6.00−0.08×age, r2=0.1827, p=0.0117). There are seven rats in the mature group. The exact age of each mature rat was unknown, but all were between postnatal age 95 and 105 days. Note that there is a discontinuity on the x-axis (age).

When we examined the longitudinal and transverse components of the residual strain of each immature rat, we found that the longitudinal strain (ϵL) showed no dependence with age (p=0.6598) and the transverse strain (ϵT) exhibited a weak but statistically significant decrease with age (r2=0.1536, p=0.0219; figure 5). When the mean longitudinal and transverse strains for the immature rats were compared, we found that mean longitudinal strain was significantly larger than the mean transverse strain (6.11±3.62% versus 3.82±2.64%, p=0.0218), and both means were significantly different than zero (p<0.0001; figure 5). As discussed above, we determined that the residual strains in mature rats were too small to measure accurately using the current technique, and the longitudinal and transverse residual strains of the mature rats were not compared.

Figure 5.

Figure 5

Open in a new tab

Longitudinal and transverse residual strain versus age in the dura mater of immature rats. Longitudinal strain (filled circle, ϵL) showed no dependence with age (p=0.6598), and transverse strain (open circle, ϵT) exhibited a weak but statistically significant decrease with age (ϵT=5.45−0.13×age, r2=0.1536, p=0.0219; regression line not shown). The mean longitudinal residual strain was significantly larger than the mean transverse residual strain (6.11±3.62% versus 3.82±2.64%, p=0.0218). A line connects the longitudinal strain and transverse strain for a given rat.

4. Discussion

The objectives of this study were to determine whether residual tensile strains are present in the dura mater of mammals in vivo, and whether the residual tensile strains are age-dependent. Our findings show that residual tensile strains are present in the dura mater of rats and that the residual tensile strains are age-dependent. We also found that the residual tensile strain in the dura mater of immature rats is on average larger in the longitudinal direction than in the transverse direction.

The main limitation of this study is that the method used to calculate the residual tensile strain present in the dura mater cannot calculate small strains that do not retract the incision edges more than the initial displacement of the edges caused by the width of the incising scalpel blade. The maximum width of the No. 15 blade scalpel used to make the incisions is 0.37 mm, as measured by digital callipers. Therefore, we assume that the blade would create an incision width of up to 0.37 mm, and that incisions measured to have a width of 0.37 mm or less may not reliably indicate the residual tensile strains present in the dura mater of that rat. For the immature rats, both the average longitudinal incision width (0.44±0.17 mm) and average transverse incision width (0.55±0.27 mm) were greater than 0.37 mm. In contrast, for the mature animals, both the average longitudinal incision width (0.05±0.02 mm) and average transverse incision width (0.07±0.03 mm) were substantially smaller than 0.37 mm. Consequently, our analysis may overestimate the strains present in the dura mater of mature rats, and so the analysis cannot determine whether there is no strain or low strain in the dura mater of mature rats. It is also worth noting that the relative error associated with the image-based measurement of incision length and width increased with decreasing magnitude of the dimension being measured. The average error, given as a percentage of the total measurement, associated with a change of one pixel was 0.28 and 1.86% for measurement of length and width of immature incisions, and 0.14 and 10.45% for measurement of length and width of mature incisions.

The study also included a number of assumptions. First, we modelled the rat dura mater as structurally isotropic (uniform material properties in all directions). The results of a study by Hamann et al. (1998) using small-angle light scattering indicated that, in general, adult human cranial dura mater is structurally isotropic for size scales greater than 1 cm2, but with localized regions of highly aligned fibres in the vicinity of the coronal sutures. It is not known whether the size scale for isotropy in immature and mature rat dura mater is proportionally smaller than that in adult humans, or whether there are similarly localized regions of highly aligned fibres in certain regions of the rat dura mater. If the rat dura mater is not isotropic at the location of the incisions used in the current study, and if this anisotropy is on a sufficiently large scale to affect the retraction of the dura mater from the incisions, then the incorrect assumption of isotropy could affect the accuracy of the calculated residual strains. Whether or not there is anisotropy in the rat dura mater, large residual strains must be present in the dura mater of immature rats to account for the large retraction observed. However, anisotropy could (at least partly) account for the finding that residual tensile strain in the longitudinal direction was larger than the residual tensile strain in the transverse direction. Therefore, future work is required to determine whether and to what extent the longitudinal and transverse strains differ. The second assumption was that we modelled the dura mater using a plane stress analysis, which disregarded the slight curvature of the dura mater where the incisions were made. That the length of the incisions was small relative to the curvature of the dura mater at the location of the incisions suggests that this is a reasonable assumption. Third, for modelling purposes, we assumed that the longitudinal and transverse directions are the directions of principal strain in the dura mater. The relatively symmetric retraction of the dura mater perpendicular to the incisions observed during the experiments suggests that this was a reasonable assumption, and that large shear strains were not present along the incisions. Fourth, we assumed that the attachment of the dura mater to the parietal bone did not interfere with opening of the incision and did not vary with age. Although we did not quantitatively measure the strength of the adhesion, the qualitative experience of the surgeon who performed the incisions was that the dura mater of rats is not firmly attached over the flat portion of the parietals, that there were not detectable differences in the strength of adhesion of the immature and mature rat dura mater, and that the immature and mature rat dura mater are equally prone to peel off the flat portion of the parietal in response to manipulation. Fifth, we assigned a Poisson's ratio of 0.45 to the rat dura mater, based on previous finite-element modelling of human dura mater (Voo et al. 1996), and we assumed that the Poisson's ratio did not change with age and that residual strains were the same in the two parietal dura mater samples from each rat. These assumptions could have affected the accuracy of the calculated strains (see appendix). For example, the mean longitudinal strain and mean transverse strain are 6.11±3.62% and 3.82±2.64% for a Poisson's ratio of 0.45 and 9.82±4.11% and 8.12±2.83% for a Poisson's ratio of 0.0. Although the present analysis was based upon the assumptions listed above, we believe that the results are suitably robust to contribute to our understanding of the mechanical environment of the dura mater. In addition, the need for these assumptions highlights the relative scarcity of information on the material properties and mechanical environment of the dura mater.

The finding that, in the dura mater of immature rats, the residual tensile strain in the longitudinal direction is larger than the residual tensile strain in the transverse direction may reflect the fact that the growth of the rat skull favours longitudinal growth during the period of development that we analysed. In a longitudinal radiographic study on the growth of the skull of black-hooded rats, Hughes et al. (1978) found that calvarial length increased more rapidly than calvarial width from before birth to postnatal day 5 and then again from postnatal day 14 to postnatal day 119. We suggest that our finding that, on average, strain in the longitudinal direction is larger than the strain in the transverse direction in immature rats between postnatal days 2 and 26 (6.11±3.62% versus 3.82±2.64%, p=0.0218) is a result of this differential growth. We hypothesize that as the cranium grows more in length than in width, the parietal dura mater, which is tethered to the cranium at the sutures, is strained more in the longitudinal direction than the transverse direction.

Cranial sutures are the primary sites of cranial growth during early postnatal development (Mednick & Washburn 1956; Duterloo & Enlow 1970). It has long been hypothesized that brain growth generates quasi-static tensile strain across the sutures (Herring 1993) and that this quasi-static tension influences the rate of bone deposition and, therefore, growth at the sutures (Enlow 1990). The mean average residual tensile strain that we have measured in the dura mater of immature rats in the present study (4.96±1.54%) is larger by two to three orders of magnitude than the tensile strains resulting from intracranial pressure that we have calculated to exist in the sutures of humans (approximately 0.0021–0.0410% at 1 month of age) and rats (0.0270±0.0190% between 2 and 60 days) (Henderson et al. 2004a). Based on this finding, the mechanosensitivity and osteogenic nature of the dura mater, and the fact that the dura mater is integrated into the fibrous tissue at the sutures, we speculate that the large residual tensile strains present in the dura mater during early postnatal development may promote osteogenic signalling from the dura mater at the site of its attachment to the sutures. If and how such signalling could influence the bone deposition rate of osteoblasts in the sutures, and therefore influence the rate and direction of cranial growth, is unclear.

The adult skeleton possesses amazing regenerative potential, being capable of healing defects and deficiencies via the formation of new bone. However, while immature animals and children under the age of 2 years maintain the capacity to heal large calvarial defects, adult animals and humans are incapable of healing the smallest of injuries (Glaser & Blaine 1940; Sirola 1960; Aalami et al. 2004). This inability of adults to heal calvarial defects secondary to trauma or disease constitutes a significant biomedical burden, as a number of techniques (including grafting of autogenous bone, application of synthetic pastes or scaffolds and insertion of alloplastic materials) must be employed to correct the defects resulting from the nearly 13 000 craniotomies and craniectomies performed annually. The estimated cost of procedures to repair these defects in the US alone was over 400 million in 2001 (Bostrom & Mikos 1997; Steiner et al. 2002). By understanding the molecular, cellular and biomechanical factors that enable immature animals to re-engineer calvarial bone, we may be able to develop clinically applicable strategies with which to repair adult calvarial defects.

Although the discrepancy in calvarial healing between children and adults has been recognized for centuries, it is only relatively recently that investigators have begun to gain insight into the biology underlying the age-dependent phenomena of calvarial regeneration. This knowledge has been gained by studying the contributions of the anatomic components that comprise a healing calvarial defect. These components include the bony edges of the defect, the overlying periosteum, and the underlying dura mater. While all of these structures have been postulated to contribute to or orchestrate the regeneration of calvarial bone in immature animals and children, data from modern in vivo studies suggest that the immature dura mater is the key regulator of calvarial regeneration (Berezowsky 1899; Hobar et al. 1993, 1996; Wang & Glimcher 1999; Mardas et al. 2002). For example, as early as the 1800s, Berezowsky (1899) reported on the inability of rabbit calvarial defects to heal if the dura mater was disturbed. That immature dura mater is required for calvarial healing has perhaps been demonstrated best by Hobar et al. (1993), who demonstrated that critical sized calvarial defects in adult guinea pigs could be rescued and converted to healing defects by the transplantation of immature dura mater. Conversely, transplantation of adult guinea pig dura mater to immature guinea pigs resulted in a loss of regenerative capacity, thus strengthening the theory that immature dura mater is a key mediator of calvarial re-ossification.

Based on this evidence suggesting that the dura mater and its stage of development are critical in ensuring successful calvarial healing, several investigators have examined dura mater in vitro, and have looked for age-related differences in the molecular and cell biology of this tissue. Greenwald et al. (2000a) have demonstrated that immature dura mater from 6-day-old rats is significantly more biologically active in vitro than dura mater from mature (60-day-old) rats, producing greater amounts of protein and/or mRNA for numerous osteogenic factors including FGF-2, TGF-β1, collagen IαI and osteocalcin. In addition, immature dura mater was shown to proliferate at an accelerated rate, and was the only dura mater capable of forming bone nodules in vitro (Greenwald et al. 2000a). Greenwald and colleagues have also demonstrated the presence of greater numbers of alkaline phosphatase-positive cells (an early marker of osteoblast differentiation) in cultured immature dura mater than in cultured mature dura mater (Greenwald et al. 2000b). These data suggest that immature dura mater, but not mature dura mater, may provide both humoral and cellular elements required for calvarial re-ossification.

Noting that the window of calvarial healing competency in humans corresponds roughly with the period of most rapid cranial growth, and that rapid growth of the brain has been hypothesized to produce tensile strain in the calvaria (Herring 1993), Fong et al. (2003) investigated the affect of equibiaxial tensile strain on gene expression in immature rat dura mater in vitro. They demonstrated that application of 10% static equibiaxial tensile strain to cultured non-suture dura mater cells derived from immature rats increased cell proliferation and expression of osteogenic growth factors, including FGF-2.

Our findings show that there are residual tensile strains in the dura mater of immature rats in vivo, and that these strains decrease by maturity. However, it is unclear whether residual strain decreases gradually, as suggested by a weak but statistically significant linear decrease with age (figure 4), or suddenly, as might be suggested by the strain data from the 22, 24 and 26 day rats (figure 4). The average residual tensile strain present in the dura mater of immature rats (postnatal age 2–26 days) was 4.96±1.54%. The study by Fong et al. (2003) showed that application of strains of the same order of magnitude (10% strain) to cultured non-suture dura mater cells derived from immature rats increased cell proliferation and expression of osteogenic growth factors, including FGF-2. In contrast, our findings suggest that there are no strains or low strains in the dura mater of mature rats, as discussed above.

Based on our current findings documenting the presence and decrease with age of residual tensile strain in rat dura mater in vivo, we speculate that large residual tensile strains present in the dura mater during growth may influence local cell biology and facilitate calvarial healing in immature animals, whereas the absence of large strains during maturity may impede healing in adult animals. Although this preliminary measurement of the residual tensile strains present in the dura mater does not provide conclusive evidence that residual tensile strain in dura mater regulates calvarial healing, the overlap between the time periods of calvarial growth, the presence of in vivo strain and the window of competency for calvaria re-ossification suggests that these processes may be intimately linked. It should be noted, however, that experiments such as those by Hobar et al. (1993) indicate that immature guinea pig dura mater remains capable of healing calvarial defects, even when transplanted into adult guinea pigs. This finding suggests that, even if residual tensile strains influence the healing capacity of immature dura mater, the residual tensile strains may not need to be present at the time of healing since they may have already exerted their effects on the differentiation of constituent cells.

Because the endosteal outer layer of the dura mater is analogous to the periosteum of the bony skeleton, it is worth noting that previous investigations have recorded large residual strains in the periostea of a number of bones. During mechanical testing of the periostea from tibiotarsi of 4- to 14-week-old chicks, Bertram and colleagues (1998) allowed samples to retract 10–15% before testing, indicating in vivo residual strains within that range. During testing of the periostea from the mandibular bodies, zygomatic arches and metacarpals of immature pigs, Popowics and colleagues (2002) measured mean in vivo residual strains ranging from 3.1% for the long-axis of the zygomatic arch to 17.2% for the long-axis of the metacarpals. A number of surgical experiments have used circumferential incisions to release periosteal strains in vivo and thereby ‘decompress’ the growth plate of the associated bone (Crilly 1972; Warrell & Taylor 1979). The results of these experiments suggest that growth plate decompression accelerates new bone formation. However, based on the findings of their mechanical testing, Bertram and colleagues (1998) suggest that circumferential incision of periostea cannot have any direct mechanical effect on the cells of the growth plate and must instead result from the release of growth-modulating factors that stimulate the growth plate. There may be similarities between the residual strains present in the dura mater and periosteum, but further work is necessary to determine if, how and to what extent the residual strains in these analogous structures influence bone growth.

In summary, we have shown that residual tensile strains exist in the dura mater of rats and that the strains are age-dependent. In addition, we found that in the dura mater of immature rats tensile strain in the primary direction of cranial growth is larger than the tensile strain in the orthogonal direction. Based on these findings, we speculate that residual tensile strains in the dura mater may influence both cranial healing and cranial growth.

Acknowledgments

The authors thank David M. Barnett for assistance with the strain analysis. This research was supported by the Fannie and John Hertz Foundation (J.H.H.), NIH R01 DE-14526, NIH R01 DE-13194, and the Oak Foundation (M.T.L.), and an ACS Resident Research Scholarship (R.P.N.).

Appendix. Effect of the assigned Poisson's Ratio and the bilateral strain assumption on calculated strains

As mentioned in §4, in our analysis, we assigned a Poisson's ratio of 0.45 to the rat dura mater, based on previous finite-element modelling of human dura mater (Voo et al. 1996), and we assumed that residual strains were the same in the two parietal dura mater samples from each rat. Because we calculated longitudinal and transverse strain (from which average strain was calculated) using a set of dependent equations (equations (2.1) and (2.2)), if the assigned Poisson's ratio or the assumption of the strains being the same was not correct, then the calculated strains would be affected. It was not possible to determine whether the residual strains were the same using the current technique, but it is customary to assume bilateral symmetry in biomechanical experiments.

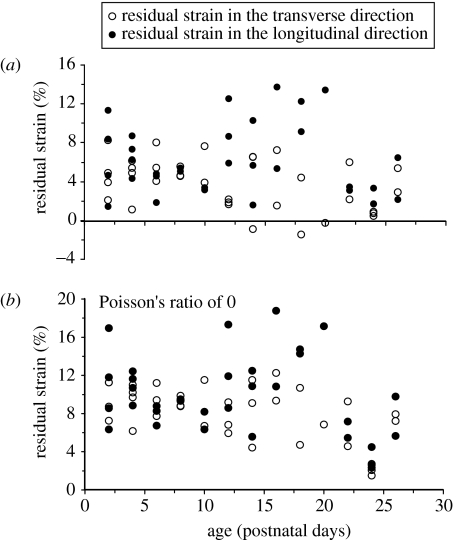
To determine the effect of the assigned Poisson's ratio on the calculated strains, we repeated the finite-element analysis using a Poisson's ratio of 0.0, determined a new set of equations analogous to equations (2.1) and (2.2), and then recalculated the longitudinal, transverse and average strains present in the dura mater of the rats. We found that using a Poisson's ratio of 0 did change the calculated strains, but did not change any of the results we reported from statistically significant to not significant. For example, when we used a Poisson's ratio of 0.45, we had calculated that longitudinal strain (ϵL) showed no dependence with age (p=0.6598), transverse strain (ϵT) decreased with age (p=0.0219), mean longitudinal strain was significantly larger than the mean transverse strain (6.11±3.62% versus 3.82±2.64%, p=0.0218), and both means were significantly different than zero (p<0.0001; figure 5 and redrawn in figure 6a). When we repeated the analysis using a Poisson's ratio of 0, we again calculated that longitudinal strain (ϵL) showed no dependence with age (p=0.1884), transverse strain (ϵT) decreased with age (p=0.0014), mean longitudinal strain was significantly larger than the mean transverse strain (9.82±4.11% versus 8.12±2.83%, p=0.0207), and both means were significantly different than zero (p<0.0001; figure 6b). In addition, for a Poisson's ratio of 0, we again calculated that the mean average residual strain of the immature rats was significantly larger than the mean average residual strain of the mature rats (8.97±2.87% versus 2.28±4.34%, p<0.0001), and the mean strain calculated in the mature rats was again of the order of the minimum measurement that could be made.

Figure 6.

Figure 6

Open in a new tab

Longitudinal (filled circle) and transverse (open circle) residual strain versus age for the immature rats calculated using a Poisson's ratio of (a) 0.45 and (b) 0. Using a Poisson's ratio of 0 did change the calculated strains but did not change any of the results we reported from statistically significant to not significant. Note that the data in (a) are the same as those presented in figure 5.

References

  1. Aalami O.O, et al. Applications of a mouse model of calvarial healing: differences in regenerative abilities of juveniles and adults. Plast. Reconstr. Surg. 2004;114:713–720. doi: 10.1097/01.prs.0000131016.12754.30. [DOI] [PubMed] [Google Scholar]
  2. Abbott A.H, Netherway D.J, Niemann D.B, Clark B, Yamamoto M, Cole J, Hanieh A, Moore M.H, David D.J. CT-determined intracranial volume for a normal population. J. Craniofac. Surg. 2000;11:211–223. doi: 10.1097/00001665-200011030-00002. [DOI] [PubMed] [Google Scholar]
  3. Berezowsky S. Untersuchungen ueber die Bedingungen und Methodik operativer Druckentlastung des Gehirnes. Dtsch. Zschr. Chir. 1899;53:53–125. [Google Scholar]
  4. Bertram J.E, Polevoy Y, Cullinane D.M. Mechanics of avian fibrous periosteum: tensile and adhesion properties during growth. Bone. 1998;22:669–675. doi: 10.1016/s8756-3282(98)00035-0. [DOI] [PubMed] [Google Scholar]
  5. Bostrom R, Mikos A. Tissue engineering of bone. In: Atala A, Mooney D.J, Vacanti J.P, Langer R, editors. Synthetic biodegradable polymer scaffolds. vol. 1. Birkhäuser; Boston: 1997. pp. 215–234. [Google Scholar]
  6. Crilly R.G. Longitudinal overgrowth of chicken radius. J. Anat. 1972;112:11–18. [PMC free article] [PubMed] [Google Scholar]
  7. Duterloo H.S, Enlow D.H. A comparative study of cranial growth in Homo and Macaca. Am. J. Anat. 1970;127:357–368. doi: 10.1002/aja.1001270403. [DOI] [PubMed] [Google Scholar]
  8. Enlow D.H. 3rd edn. Saunders; Philadelphia: 1990. Facial growth. [Google Scholar]
  9. Fong K.D, Warren S.M, Loboa E.G, Henderson J.H, Fang T.D, Cowan C.M, Carter D.R, Longaker M.T. Mechanical strain affects dura mater biological processes: implications for immature calvarial healing. Plast. Reconstr. Surg. 2003;112:1312–1327. doi: 10.1097/01.PRS.0000079860.14734.D6. [DOI] [PubMed] [Google Scholar]
  10. Fung Y.C. Springer; Heidelberg: 1984. Biodynamics: circulation. [Google Scholar]
  11. Glaser M.A, Blaine E.S. Fate of cranial defects secondary to fracture and surgery. Radiology. 1940;34:671–684. [Google Scholar]
  12. Greenwald J.A, et al. Biomolecular mechanisms of calvarial bone induction: immature versus mature dura mater. Plast. Reconstr. Surg. 2000;105:1382–1392. doi: 10.1097/00006534-200004040-00018. [DOI] [PubMed] [Google Scholar]
  13. Greenwald J.A, Mehrara B.J, Spector J.A, Fagenholz P.J, Saadeh P.B, Steinbrech D.S, Gittes G.K, Longaker M.T. Immature versus mature dura mater. II. Differential expression of genes important to calvarial reossification. Plast. Reconstr. Surg. 2000;106:630–638. [PubMed] [Google Scholar]
  14. Gregersen H, Kassab G.S, Fung Y.C. The zero-stress state of the gastrointestinal tract: biomechanical and functional implications. Dig. Dis. Sci. 2000;45:2271–2281. doi: 10.1023/a:1005649520386. [DOI] [PubMed] [Google Scholar]
  15. Hamann M.C, Sacks M.S, Malinin T.I. Quantification of the collagen fibre architecture of human cranial dura mater. J. Anat. 1998;192 (Pt 1):99–106. doi: 10.1046/j.1469-7580.1998.19210099.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Han H.C, Fung Y.C. Direct measurement of transverse residual strains in aorta. Am. J. Physiol. 1996;270:H750–H759. doi: 10.1152/ajpheart.1996.270.2.H750. [DOI] [PubMed] [Google Scholar]
  17. Henderson J.H, Carter D.R. Mechanical induction in limb morphogenesis: the role of growth-generated strains and pressures. Bone. 2002;31:645–653. doi: 10.1016/s8756-3282(02)00911-0. [DOI] [PubMed] [Google Scholar]
  18. Henderson J.H, Chang L.Y, Song H.M, Longaker M.T, Carter D.R. Age-dependent properties and quasi-static strain in the rat sagittal suture. J. Biomech. 2004 doi: 10.1016/j.jbiomech.2004.07.037. doi::10.1016/j.jbiomech.2004.07.037. [DOI] [PubMed] [Google Scholar]
  19. Henderson J.H, Longaker M.T, Carter D.R. Sutural bone deposition rate and strain magnitude during cranial development. Bone. 2004;34:271–280. doi: 10.1016/j.bone.2003.10.007. [DOI] [PubMed] [Google Scholar]
  20. Herring S.W. Epigenetic and functional influences on skull growth. In: Hanken J, Hall B.K, editors. The skull. vol. 1. University of Chicago Press; Chicago: 1993. pp. 153–206. [Google Scholar]
  21. Hobar P.C, Schreiber J.S, McCarthy J.G, Thomas P.A. The role of the dura in cranial bone regeneration in the immature animal. Plast. Reconstr. Surg. 1993;92:405–410. doi: 10.1097/00006534-199309000-00003. [DOI] [PubMed] [Google Scholar]
  22. Hobar P.C, Masson J.A, Wilson R, Zerwekh J. The importance of the dura in craniofacial surgery. Plast. Reconstr. Surg. 1996;98:217–225. doi: 10.1097/00006534-199608000-00003. [DOI] [PubMed] [Google Scholar]
  23. Hughes P.C, Tanner J.M, Williams J.P. A longitudinal radiographic study of the growth of the rat skull. J. Anat. 1978;127:83–91. [PMC free article] [PubMed] [Google Scholar]
  24. Mardas N, Kostopoulos L, Karring T. Bone and suture regeneration in calvarial defects by e-PTFE-membranes and demineralized bone matrix and the impact on calvarial growth: an experimental study in the rat. J. Craniofac. Surg. 2002;13:453–462. doi: 10.1097/00001665-200205000-00017. [DOI] [PubMed] [Google Scholar]
  25. Mednick L.W, Washburn S.L. The role of the sutures in the growth of the braincase of the infant pig. Am. J. Phys. Anthropol. 1956;14:175–191. doi: 10.1002/ajpa.1330140215. [DOI] [PubMed] [Google Scholar]
  26. Popowics T.E, Zhu Z, Herring S.W. Mechanical properties of the periosteum in the pig, Sus scrofa. Arch. Oral Biol. 2002;47:733–741. doi: 10.1016/s0003-9969(02)00065-1. [DOI] [PubMed] [Google Scholar]
  27. Sirola K. Regeneration of defects in the calvaria. Ann. Med. Exp. Biol. Fenn. 1960;38:1–87. [PubMed] [Google Scholar]
  28. Steiner C, Elixhauser A, Schnaier J. The healthcare cost and utilization project: an overview. Eff. Clin. Pract. 2002;5:143–151. [PubMed] [Google Scholar]
  29. Vaishnav R.N, Vossoughi J. Estimation of residual strain in aortic segments. In: Hall C.W, editor. Biomedical engineering II: recent development: proceedings of the Second Southern Biomedical Engineering Conference. vol. 330–333. Pergamon Press; Oxford: 1983. [Google Scholar]
  30. Vaishnav R.N, Vossoughi J. Residual stress and strain in aortic segments. J. Biomech. 1987;20:235–239. doi: 10.1016/0021-9290(87)90290-9. [DOI] [PubMed] [Google Scholar]
  31. Voo K, Kumaresan S, Pintar F.A, Yoganandan N, Sances A., Jr Finite-element models of the human head. Med. Biol. Eng. Comput. 1996;34:375–381. doi: 10.1007/BF02520009. [DOI] [PubMed] [Google Scholar]
  32. Wang J, Glimcher M.J. Characterization of matrix-induced osteogenesis in rat calvarial bone defects. I. Differences in the cellular response to demineralized bone matrix implanted in calvarial defects and in subcutaneous sites. Calcif. Tissue Int. 1999;65:156–165. doi: 10.1007/s002239900676. [DOI] [PubMed] [Google Scholar]
  33. Warrell E, Taylor J.F. The role of periosteal tension in the growth of long bones. J. Anat. 1979;128:179–184. [PMC free article] [PubMed] [Google Scholar]
  34. Westergaard H.M. Bearing pressures and cracks. J. Appl. Mech. 1939;6:A49–A53. [Google Scholar]

Articles from Journal of the Royal Society Interface are provided here courtesy of The Royal Society

RESOURCES