Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2006 Sep 1;91(10):3937–3945. doi: 10.1529/biophysj.106.088534

Dielectrophoresis as a Tool to Characterize and Differentiate Isogenic Mutants of Escherichia coli

M Castellarnau *,†, A Errachid *,†, C Madrid *,‡, A Juárez *,‡, J Samitier *,†
PMCID: PMC1630483  PMID: 16950844

Abstract

In this study we report on an experimental method based on dielectrophoretic analysis to identify changes in four Escherichia coli isogenic strains that differed exclusively in one mutant allele. The dielectrophoretic properties of wild-type cells were compared to those of hns, hha, and hha hns mutant derivatives. The hns and hha genes code respectively for the global regulators Hha and H-NS. The Hha and H-NS proteins modulate gene expression in Escherichia coli and other Gram negative bacteria. Mutations in either hha or hns genes result in a pleiotropic phenotype. A two-shell prolate ellipsoidal model has been used to fit the experimental data, obtained from dielectrophoresis measurements, and to study the differences in the dielectric properties of the bacterial strains. The experimental results show that the mutant genotype can be predicted from the dielectrophoretic analysis of the corresponding cultures, opening the way to the development of microdevices for specific identification. Therefore, this study shows that dielectrophoresis can be a valuable tool to study bacterial populations which, although apparently homogeneous, may present phenotypic variability.

INTRODUCTION

Dielectrophoresis is a phenomenon, first detailed in the early 1950s, which explains the translational motion of noncharged dielectric particles brought about by the application of nonuniform electric fields (1). Depending on the electrode configuration and geometry used to produce the AC electric field, as well as the magnitude and phase variations of the field between the different electrodes, we can define different AC-electrokinetic methods such as common dielectrophoresis (DEP), electrorotation, or traveling-wave dielectrophoresis. Dielectrophoresis has been used to selectively trap, manipulate, and separate particles in liquids (2–5). Dielectrophoretic devices have also been widely used for biological applications, where the effect of dielectrophoretic forces on both eukaryotic and prokaryotic cells has been examined. Examples of applications include differentiation between viable and nonviable cells (2,3,6–8), separation and/or characterization of different types of cells (9–14), and analysis of infected cells (15) or of cells exposed to drugs or toxins (16–18). Dielectrophoresis has also been used to study and manipulate biomolecules such as DNA and proteins (19,20).

To date, dielectrophoresis has not been combined with approaches such as bacterial genetics. Here, we have examined whether dielectrophoresis can be used to distinguish between wild-type bacterial cells and their mutant derivatives with a modified phenotype. As a specific model we have studied the dielectrophoretic properties of wild-type cells from Escherichia coli and mutant derivatives lacking either one or both of the global regulators H-NS and Hha. H-NS and Hha proteins belong to the family of bacterial nucleoid-associated proteins (21,22). Both proteins interact to modulate gene expression, and mutants lacking one, or both, of these regulators show altered levels of different proteins (23–25). So we will first present the phenomenological description of the dielectrophoresis using E. coli bacterial strains and the relation between the main parameters of the dielectric model of these bacteria and the experimental results.

DEP fundamentals

When a dielectric particle is placed under the influence of an applied AC field, a dipole moment is induced within the particle. If the field is inhomogeneous the polarized particle experiences a translational force, known as the dielectrophoretic force (1), whose magnitude and direction depends on the electrical properties of the particle and its surrounding medium. This force also depends on the magnitude and frequency of the applied electric field.

For spherical particles, the time-averaged DEP force is (26)

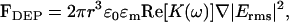graphic file with name M1.gif (1)

where r is the particle radius, ɛ0 is the permittivity of free space, ɛm is the real part of the permittivity of the suspending medium, and Erms is the root mean-square electric field. The factor K(ω) (the Clausius-Mossotti factor) depends on the complex permittivity of both the particle and the medium and is a measure of the effective polarizability of the particle. In the case of spherical particles, this factor is given by

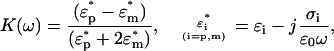graphic file with name M2.gif (2)

where the indices p and m refer to the particle and the medium, respectively. The values ɛ and σ are, respectively, the permittivity and the conductivity of the dielectric, ω is the angular frequency of the applied field (ω = 2πf), and 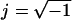Inline graphic. Two different experimental conditions can be established. When Re[K(ω)] > 0, the particles move toward regions where the maximum electric fields occur and the phenomenon is called positive dielectrophoresis (p-DEP). Alternatively, when the particle polarizability is low enough that Re[K(ω)] becomes negative, i.e., Re[K(ω)] < 0, then the particles move toward regions with minimum electric fields. This case is called negative dielectrophoresis (n-DEP). For spherical particles, the interval range of Re[K(ω)] is between −0.5 and 1.

Conventional dielectrophoresis (DEP) experiments consist of visually monitoring the cell response to changes in the frequency of the applied electric field, to determine the crossover frequencies (which correspond to the frequencies where the dielectrophoresis force is null). The values of these crossover frequencies depend on the medium conductivity and on the properties of the dielectric cells. Consequently, this allows cells with different dielectric properties to be compared and identified. The main purpose of this article is to demonstrate that, by using the dielectrophoresis technique, it is possible to distinguish between different mutant bacterial strains, when compared with the wild-type strain. A qualitative explanation of the experimental results is given by considering a dielectric model, which can also be interpreted from a biological point of view. This work could lead to microfluidic DEP separation devices that are able to identify and separate bacterial cells of different strains exhibiting subtle differences.

Dielectric bacterial cell model and dielectrophoresis simulation

One of the earliest models to explain the electrical response of cells was proposed by Hoeber, who demonstrated that the cell could be described as a sphere of highly conducting cytoplasm surrounded by an insulating membrane. Schwan used a combination of the Maxwell and Wagner theories to describe, dielectrically, the dispersion of biological cells suspended in an electrolyte (27). If one considers one sphere contained inside another, this process can be repeated many times to model different cell structures (6,8,28–32). Therefore, multishelled systems, where the cytoplasm is bounded by membranes of finite thickness, are required to model the dielectric response of cells. Each interface, separating the different dielectric layers, introduces a Maxwell-Wagner relaxation process.

Optical and atomic force microscopy images reveal that the E. coli bacteria cells have an ellipsoid shape with a cylindrical section (rod-shaped) as shown in Fig. 1. However, there is no analytical description for rod-shaped systems. Therefore, a prolate ellipsoid-of-revolution multi-shell model has been used to describe the dielectric properties of the bacteria in suspension. A two-shell model consisting of cytoplasm surrounded by a membrane and a cell wall has been adapted (31,32), as shown in the schematic diagram in Fig. 1. The model includes permittivity and conductivity parameters for the suspending medium and for all of the shells that make up the cell. As the polarization factor used in the DEP force definition (Eq. 1), and hence the Clausius-Mossotti factor (Eq. 2), is valid only for spherical particles, it is necessary to modify this factor taking into account the ellipsoidal shape of the cells (26,32,33). This consideration defines the three components for this factor for the three possible axes of polarization that in the case of homogeneous ellipsoids are expressed as

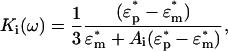graphic file with name M4.gif (3)

where Ai is a component of the depolarization factor along any one of the three axes of the ellipsoid (i = x, y, z). For a prolate spheroid this component, at the direction of its major axis, is given by

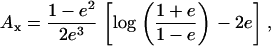graphic file with name M5.gif (4)

where

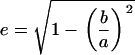graphic file with name M6.gif (5)

is the eccentricity, and a and b are the major and minor axes of the ellipsoid, respectively. Due to the symmetry of the ellipsoid of revolution, the components of the depolarization factor at the two other axes of the prolate ellipsoid (i = y, z) have the same value, given as

graphic file with name M7.gif (6)

FIGURE 1.

FIGURE 1

Open in a new tab

Diagram of the ellipsoid multishell model considered for E. coli cells (left) and an atomic-force microscopy topography image of a single Escherichia coli cell (right). Geometrical parameters considered: a = 3/2 μm; b = a/2 μm; dmem = 8 nm; and dwall = 50 nm (although, in the present cell model, the shells represented by layers between two different surfaces of confocal ellipsoids have nonuniform thickness all over the cell surfaces, the values of dmem and dwall, are approximate to a constant value).

However, when a multishell system is considered, the complexity of the Clausius-Mossotti factor is increased. Huang and co-workers provided a complete analytical expression to calculate this factor for a prolate spheroid with a single shell (31,32), which can be extended to multiple layers. A detailed calculation of the Clausius-Mossotti factor for a two-shell prolate ellipsoid of revolution is given in Appendix A.

The real part of the Clausius-Mossotti factor was modeled with respect to the frequency of the applied field, using Eq. A11. This was completed along the three directions of polarization, at different medium conductivities. For this purpose, the dielectric parameters for E. coli bacterial cells obtained from electrorotation measurements by Mietchen et al. (34) were used. In terms of electrical impedance, and in the simple electrical model, the cell wall and the cytoplasmic membrane are mainly considered as insulating layers, and the cytoplasm as a conductive layer. We can therefore model the cell as a double capacitor in series with a resistor. This means that the cell has a characteristic relaxation time that depends on the dielectric properties of the multishell system, and which determines the frequency threshold at which the system depends on the properties of the cytoplasm or the cell membrane (i.e., the cell wall and cytoplasmic membrane properties).

Fig. 2 A shows that a first crossover frequency (fc1) can be found in the 500 kHz–10 MHz frequency range, for certain medium conductivities (up to 5.5 · 10−2 S · m−1). A second crossover frequency (fc2) is found in the 55–110 MHz frequency range for all the medium conductivities considered in this simulation (i.e., 10−3 S · m−1 to 0.4 S · m−1). As the medium conductivity increases, the values of fc1 and fc2 tend to converge on one another, until a certain conductivity value (∼0.4 S · m−1) is reached where the cells are confined to the n-DEP regime. At high conductivities (beyond 0.15 S · m−1), the value of the real part of the Clausius-Mossotti factor decreases rapidly at frequencies within the p-DEP regime and therefore, under these medium conductivity conditions, the DEP force will be very weak. This will severely hinder the observation of the crossover frequencies.

FIGURE 2.

FIGURE 2

Open in a new tab

(A) Evolution of the real part of the Clausius-Mossotti factor with changes in the medium conductivity (in S · m−1); fc1 and fc2 refer to the crossover frequencies. (B) Sensitivity study of the two-shell model parameters on the real part of the Clausius-Mossotti factor (see text for the definitions of the model parameters). A decrease in the dielectric parameters in each case produces the changes in the modeled plot as indicated by arrows in the different frequency regions.

Fig. 2 B summarizes the influence of each parameter of the two-shell ellipsoidal model used on the evolution of the real part of the Clausius-Mossotti factor. At the low frequency range (1–100 kHz), the main contributions are due to the cytoplasmic membrane conductivity (σmem) and, to a lesser degree, the cell wall conductivity (σwall). When the frequency increases (100 kHz–10 MHz), changes in the real part of the Clausius-Mossotti factor are also related with the cytoplasmic membrane permittivity (ɛmem). Finally, in the high frequency range (10 MHz–1 GHz), the influence of the cytoplasm becomes more important, mainly due to the cytoplasm conductivity (σcyto). However, there is still significant influence from the cytoplasmic membrane and cell wall permittivities (ɛmem and ɛwall).

Therefore, the cell wall and cytoplasmic membrane dielectric parameters can be considered to influence the whole frequency range analyzed, especially at frequencies <10 MHz, whereas the cytoplasm parameters became significant at high frequencies.

MATERIALS AND METHODS

Experimental setup

Complementary pairs of electrodes (in U- and T-configurations), polarized with the aforementioned AC signals, are used to generate the inhomogeneous electric field necessary to produce the DEP forces (Fig. 3) (35,36). The integrated DEP electrode devices have been fabricated on (100)-oriented, 100-mm diameter p-type silicon wafers with a resistivity of 4–40 Ω · cm. The castellated microelectrodes are produced by deposition of 150 nm of Pt onto a 30 nm Ti layer, after which the wafer was diced and cleaned. Typical dimensions of the internal U-shaped area of the DEP microelectrodes are 70 × 70 μm2. Note that the DEP microelectrodes are in contact with the liquid solution, but there are no electrolysis effects because the applied electric field is alternating and of relatively high frequency.

FIGURE 3.

FIGURE 3

Open in a new tab

Optical microscopy image of a pair of electrodes in U- and T-configurations for cell handling by DEP.

To allow the devices to be immersed in a liquid solution during measurements, they were glued to a printed circuit board and electrical connection was made by wire-bonding. The electrical contacts were insulated using an epoxy resin (EPO-TEK No. H70E-2LC, Epoxy Technology, Billerica, MA).

Two function generators (Agilent model No. 33250A for low frequencies or model No. HP8657A for high frequencies; Agilent, Santa Clara, CA) were used to provide AC signals, of 6–10 V peak-to-peak with a variable frequency in the 10 kHz–200 MHz range, necessary to produce the DEP force. Sample conductivity was monitored using a conductivity meter (Corning conductivity meter, model No. 441; Corning, NY), while progressively adding aliquots of NaCl to the sample solution. All the experiments were carried out at room temperature (22–25°C). Finally, cell trapping and release during DEP experiments were observed using a Nikon Eclipse model No. L150 reflectance microscope fitted with a digital camera (Nikon, Tokyo, Japan). Images were recorded using a personal computer with an image acquisition card. The crossover frequencies were determined by optical observation of the cell behavior at the frequency regions where there is a transition from one DEP regime to other (from p-DEP to n-DEP or from n-DEP to p-DEP) until no predominant DEP force was observed (frequency where the DEP forces were null).

Biological samples

The different bacterial strains used in this study are listed in Table 1. The different strains were grown in Luria Bertani medium (10 g/l NaCl, 10 g/l tryptone, 5 g/l yeast extract). Antibiotics were used at the following concentrations: kanamycin (25 μg/ml); ampicillin (50 μg/ml); cloramphenicol (50 μg/ml); and tetracycline (15 μg/ml). Overnight liquid cultures were centrifuged (4000 rpm), washed, and resuspended in distilled water. Samples were then used for the dielectrophoretic studies while progressively increasing the medium conductivity with NaCl.

TABLE 1.

Genotype and phenotype description of the bacterial strains used in this work

Strain Genotype Phenotype Reference
5K F−, hdsR, hdsM, thr, thi, leu, lacZ Wild-type strain (37)
Hha-3 5K hha∷Tn5phoA Hha− mutant (38)
5K hns 5K hns∷ampR H-NS− mutant (25)
Hha-3 hns Hha3 hns∷ampR Double Hha− H-NS− mutant (25)
Open in a new tab

RESULTS AND DISCUSSION

A comparison of the evolution of the crossover frequencies measured at different medium conductivities has been exhaustively determined for the four bacterial suspensions investigated here. As previously stated, the high medium conductivities hinder the observation of the crossover frequency. Therefore, the experimental medium conductivities were restricted into a range where n-DEP and p-DEP regimes were clearly observable. In the conductivity range, between 10−3 S · m−1 and 0.13 S · m−1, two frequency regions where DEP forces are null were observed. The first region, from 10 kHz to 10 MHz, a first DEP crossover frequency is observed (fc1) that is governed by the dielectric parameters of the cell membrane. At higher frequencies, from 10 MHz to 200 MHz, a second DEP crossover frequency (fc2) is seen that mainly depends on the dielectric parameters of the cytoplasm.

The experimental values obtained and their evolutions with the media conductivity have been fitted using the two-layer dielectric model defined in the previous section. All the experiments showed a clear separation between the crossover frequency values for the parental E. coli 5K strain and the different mutant strains, when studying the evolution of the first crossover frequency (fc1) at the low frequency range. All the mutant derivatives showed similar fc1 values (Fig. 4). However, when the high frequency region was examined, differences in the crossover frequency values did not follow the same pattern. Second crossover frequency values (fc2) of the parental E. coli and the hha mutant derivative could not be distinguished. In contrast, fc2 values for the hns mutant and double hha hns mutant were much lower compared with the other two strains (Fig. 4). The hns and double mutant hha hns mutants can be readily differentiated from wild-type cells both at the low and high frequency regions. However, hha mutants can only be distinguished from wild-type cells at the low frequency region.

FIGURE 4.

FIGURE 4

Open in a new tab

Evolution of crossover frequencies, fc1 and fc2, with changes in the medium conductivity (symbols correspond to experimental data; solid lines correspond to the fitted two-layer model; dashed lines correspond to the predicted evolution of the crossover frequencies using the dielectric parameters obtained from each fitting into the model).

The fitting using the two-layered ellipsoidal model for bacteria includes eight dielectric parameters (i.e., six variable, the conductivities and relative permittivities of each of the layers plus the cytoplasm; and two fixed, the conductivity and relative permittivity of the surrounding medium), and four geometric parameters (the width and length of the cytoplasm, the thickness of cytoplasmic membrane, and the thickness of the cell wall). In this context, it would be very difficult to quantitatively pinpoint the change in the dielectric parameters obtained from the fitting of the available experimental data for the different bacterial strains. In our case (isogenic derivatives of the same strain, differing only in one or two mutant alleles), it can be assumed that the four geometric parameters are similar, and thus they can be fixed (a = 3/2 μm, b = a/2, dmem = 8 nm, and dwall = 50 nm). In addition, from the dielectric parameters, the relative permittivity of the surrounding medium can also be considered as constant in the different experiments (ɛm = 80 · ɛ0). Finally, the medium conductivity is a known value taken from the conductivity-meter readings.

The experimental data consists of two sets of crossover frequencies (fc1 and fc2) obtained at different medium conductivities. Using a nonlinear least-squares fit (MatLab, The MathWorks, Natick, MA), the fitting procedure modifies the dielectric parameters of the two-shell model considered (Eq. A11) to try to match the crossover frequencies of the real part of the Clausius-Mossotti factor with the experimental results measured for each strain. The first step was to fit the experimental crossover frequencies obtained from the E. coli 5K strain, which were used to define our reference set of dielectric parameters. Initial values were based on the dielectric parameters obtained by Mietchen et al. (34). Table 2 compares these initial values with those obtained from our fitting procedure. From this comparison it is observed that σcyto, ɛcyto, ɛmem, and ɛwall values adapt fairly well to those given by Mietchen and co-workers, whereas σmem and σwall values were significantly different. Nevertheless, it should be pointed out that different E. coli strains may significantly differ in their cell envelope composition (e.g., through the protein composition of the cytoplasmic membrane or the lipopolysaccharide composition in the outer membrane). Therefore, as the goal of our study is to compare values from strain 5K and the different mutant derivatives, we further consider the different values from our fitting.

TABLE 2.

Comparison of the dielectric parameter values from Mietchen et al. (34) adjustments to electrorotation data for E. coli and the two-shell prolate ellipsoidal model adjusted for E. coli strain 5K (relative variation in brackets)

Source σcyto (S · m−1) σmem (1e-6 S · m−1) σwall (1e-3 S · m−1) ɛcyto/ɛ0 ɛmem/ɛ0 ɛwall/ɛ0
Mietchen et al. 0.50 1 7 50 8 77
E. coli 5K fitting 0.48 (4%) 259 (2.6e4%) 58 (728%) 49.8 (0.4%) 9.8 (22%) 78 (1.3%)
Open in a new tab

Geometrical parameters: a = 3/2 μm; b = a/2 μm; dmem = 8 nm; and dwall = 50 nm. Dielectric medium parameters: ɛm = 80 · ɛ0; and σm the different measured medium conductivity points in the 10−3–0.13 S · m−1 range.

A sensitivity study of the dielectric parameters of the two-shell model was carried out to determine which parameters could be considered as the main variables for the fitting and which ones could be kept fixed when comparing the experimental data for the different strains. For this purpose we varied each parameter of the model to examine whether it produced the observed modifications in the crossover frequencies. Each time we have initialized the fitting with the parameters obtained for our E. coli strain 5K cells. For instance, in Fig. 4, given a medium conductivity of 0.1 S · m−1, the maximum relative differences on the crossover frequencies, comparing the different strains, are 65% and 36% for fc1 and fc2, respectively. Fig. 5 summarizes this study.

FIGURE 5.

FIGURE 5

Open in a new tab

Sensitivity study of the relative variation in the dielectric parameters of the two-shell model. (A–C) fc1; and (D–F) fc2. The evolution of the crossover frequencies or the zeros of the real part of Clausius-Mossotti factor (from Eq. A11) were studied changing each one of the six dielectric parameters from the different layers of the two-shell model (ɛcyto, σcyto, ɛmem, σmem, ɛwall, σwall). Geometrical parameters were fixed to a = 3/2 μm; b = a/2 μm; dmem = 8 nm; and dwall = 50 nm. Only the cases that can produce a change on fc1 or fc2 comparable to the changes observed experimentally are here presented.

The first crossover frequency, fc1, strongly depends on the cytoplasmic membrane parameters (σmem and ɛmem) and to a lesser degree on the cell wall conductivity (σwall), whereas fc2 mainly depends on the cytoplasm conductivity (σcyto). Next, the influence of the cell envelope properties (ɛmem and ɛwall) on fc2 is examined. In Fig. 5 E, we observe that a decrease in ɛmem implies a decrease in fc2, but this change also induces an increase in fc1 (Fig. 5 B) that can only be compensated with an increment in σmem (Fig. 5 A), which is contradictory because the cytoplasmic membrane will become more conductive and insulating at the same time. Therefore, only increases in ɛmem will be considered for the adjustment, and consequently no great influence on fc2 is expected. On the other hand, Fig. 5 F shows that a large change in ɛwall (close to 85%) is needed to achieve the desired change in fc2, but again, if we assume that an increment in the cell wall conductivity is needed to fit fc1 (i.e., the cell wall becomes more conductive), then a decrease in the cell wall permittivity (i.e., the cell wall becomes more insulating) is nonsensical. The rest of the cases, which do not appear in this graph, have null or very little effect on the variation of the crossover frequencies.

Taking these points into consideration, we decided to fix the cytoplasm (ɛcyto) and cell wall (ɛwall) permittivities, and vary the other dielectric parameters of the model (ɛmem, σmem, σwall, and σcyto) to correlate the experimental data from the double and single mutant derivatives. The dielectric parameters were initialized to the values obtained from the fitting to the E. coli 5K strain. The best fitting results for these parameters, which adjust to the experimental data, are shown in Table 3.

TABLE 3.

Results from the two-shell model adjustment for the different bacteria strains compared with the E. coli strain 5K case (relative variation in brackets)

Strain σcyto (S · m−1) σmem (1e-6 S · m−1) σwall (1e-3 S · m−1) ɛmem/ɛ0
E. coli 5K 0.48 259 58 10
Hha-3 hns 0.33 (33%) 441 (70%) 70 (21%) 25 (150%)
Hha-3 0.48 (0%) 498 (92%) 67 (15%) 18 (80%)
5K hns 0.31 (35%) 400 (54%) 89 (53%) 18 (80%)
Open in a new tab

Geometrical parameters: a = 3/2 μm; b = a/2 μm; dmem = 8 nm; and dwall = 50 nm. Dielectric medium parameters: ɛm = 80 · ɛ0; and σm the different measured medium conductivity points in the 10−3–0.13 S · m−1 range.

From this fitting analysis we can conclude that all the mutant derivatives display similar envelope dielectric properties, with higher values than those from the parental 5K strain (see relative variations in Table 3). These results suggest that the cell envelopes of both the single and double mutants are more conductive than those of the E. coli 5K. On the other hand, the different mutant strains do not follow the same behavior with respect to the cytoplasmic conductivity. When compared with the parental 5K strain, the cytoplasmic conductivity of both the hns and double hha hns mutants were significantly lower. In contrast, the value of the hha mutant is similar to that of the 5K strain. The cytoplasms of the double mutant and the single hns mutant are therefore less conductive than the cytoplasm of the E. coli 5K strain and the single hha mutant.

From our previous knowledge of the properties of hha and hns mutants, the above dielectrophoretic data can be interpreted in the following way. The H-NS protein plays a role in modulating bacterial gene expression. Expression of ∼5% of the E. coli genes is affected in hns mutants (39). The Hha protein interacts with the H-NS to modulate gene expression (23,24), but most likely the Hha is required to participate in only a subset of the genes modulated by H-NS. Examples of the genes modulated by both the Hha and H-NS are the toxin α-hemolysin (24,40) and the outer membrane protein OmpA (our unpublished results). Most likely, coregulation by H-NS and Hha of genes encoding for cell envelope proteins, such as OmpA, results in drastic alterations in the cell envelope in both hns and hha cells. Thus, both hha and hns mutants show similar alterations in the dielectric properties of the respective cell envelopes and the double hha hns mutant as well.

With respect to the cytoplasm, it should be considered that H-NS is an abundant protein, ∼20,000 copies/cell (21), whereas Hha is less abundant (41). In addition to modulating gene expression, H-NS plays a role structuring the bacterial nucleoid. Alterations in chromosomal DNA structure that occur in hns might account for the change in the dielectric properties of the cytoplasm. This is not the case for hha mutants. Changes in the dielectric properties of the cytoplasm of the double hha hns mutant will probably be exclusively caused by the hns mutation.

These results show that E. coli 5K, Hha-3, and 5K-hns strains can be identified using dielectrophoretic experiments. Therefore, this experimental technique can be used to develop microfluidic devices to identify small differences in homogeneous bacterial populations. In different pathogenic Gram negative microorganisms, subtle changes in envelope components occur (antigenic or phase variations) (42). It appears interesting to use dielectrophoresis to better characterize and define the antigenic variation processes that occur in some of these pathogens.

CONCLUSIONS

Dielectrophoresis has been used to identify subtle changes in bacteria cell conformation, due to mutations, that affect the global modulators Hha and H-NS. A dielectric model has been adapted to fit the experimental data of the different bacterial strains. The experimental results show that it is possible to identify, and consequently would be possible to separate, the different mutant strains from the wild-type E. coli 5K strain. Moreover, these results allow microfluidic devices to be designed, incorporating dielectrophoretic microelectrodes, which could be able to identify and separate cells from apparently homogeneous populations that nevertheless include bacterial strains exhibiting subtle phenotypic differences.

Acknowledgments

The authors thank Mr. R. Casanella for his previous work on DEP, Mrs. M. C. Jaramillo for assistance in the preparation of samples, and of Dr. C. Mills for comments with respect to this work.

Dr. A. Errachid acknowledges support from the Ramon y Cajal program. Financial support for this work, provided by the Spanish Ministry of Science and Technology under projects No. TIC2001-3569-C02-01/02 and TIC2004-06514, is gratefully acknowledged.

APPENDIX A

Taking the dielectric two-shell model for a bacteria with a prolate ellipsoidal shape, as shown in Fig. 1, the Clausius-Mossotti factor can be defined in three steps by considering the relationship between each of the neighboring layers, using the analytical expressions provided by Huang et al. (31,32). Beginning with the two inner layers (the cytoplasm and the cytoplasmic membrane), the effective dipole factor of these two layers can be defined as

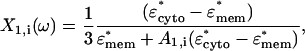graphic file with name M8.gif (A1)

where Ai is the component of the depolarization factor along the three axes of the ellipsoid (i = x, y, z). For a prolate spheroid of revolution, this factor along the direction of its major axis is given by

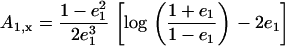graphic file with name M9.gif (A2)

and

graphic file with name M10.gif (A3)

As Ax + Ay +Az = 1, and due to the rotational symmetry of the cell, the other two components of the depolarization factor have the same value and are defined as

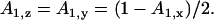graphic file with name M11.gif (A4)

Once the effective dipole moment has been defined for the two inner layers, the influence of the next outer layer is considered and the effective dipole moment for the whole particle is given by

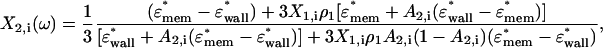graphic file with name M12.gif (A5)

where (i = x, y, z). Again the components of the depolarization factor are defined as in Eq. A2 and Eq. A4 but the eccentricity changes to

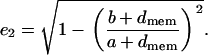graphic file with name M13.gif (A6)

Approximating the thickness of the coating layer as a constant (28), then the volume ratio between these layers is given by

graphic file with name M14.gif (A7)

Finally the Clausius-Mossotti factor can be expressed considering the relationship with the surrounding medium as

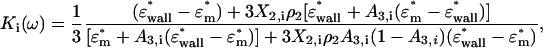graphic file with name M15.gif (A8)

where X2 is defined in Eq. A5 taking into account the relationship with the inner layers of the cell, and A3 and ρ2 are expressed following the same procedure as before. Therefore, on this occasion, the eccentricity is described for the whole cell as

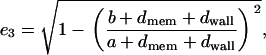graphic file with name M16.gif (A9)

and considering the same assumptions as above, the volume ratio is

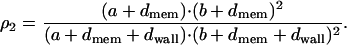graphic file with name M17.gif (A10)

In addition, as the dielectrophoretic force at the crossover frequencies is null, no assumptions of preferential orientation of the cells can be considered, because the cells are randomly oriented (this is not the case under the p-DEP or n-DEP regimes). Therefore, using Eq. A8, the Clausius-Mossotti factor can be calculated along the three axes of polarization of the two-shell prolate spheroid of revolution considered to describe the cells. Finally, the DEP behavior can be described using the average of the real part of the Clausius-Mossotti factor for the three possible axes of polarization:

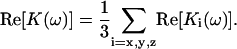graphic file with name M18.gif (A11)

References

  • 1.Pohl. H.A. 1978. Dielectrophoresis. Cambridge University Press, New York.
  • 2.Pohl, H. A., and I. Hawk. 1966. Separation of living and dead cells by dielectrophoresis. Science. 152:647–649. [DOI] [PubMed] [Google Scholar]
  • 3.Mason, B. D., and E. G. Hammond. 1971. Dielectrophoretic separation of living cells. Can. J. Microbiol. 17:879–888. [DOI] [PubMed] [Google Scholar]
  • 4.Fiedler, S., S. G. Shirley, T. Schnelle, and G. Fuhr. 1998. Dielectrophoretic sorting of particles and cells in a microsystem. Anal. Chem. 70:1909–1915. [DOI] [PubMed] [Google Scholar]
  • 5.Morgan, H., M. P. Hughes, and N. G. Green. 1999. Separation of submicron bioparticles by dielectrophoresis. Biophys. J. 77:516–525. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Huang, Y., R. Holzel, R. Pethig, and X.-B. Wang. 1992. Differences in the AC electrodynamics of viable and non-viable yeast cells determined through combined dielectrophoresis and electrorotation studies. Phys. Med. Bid. 37:1499–1517. [DOI] [PubMed] [Google Scholar]
  • 7.Suehiro, J., R. Hamada, D. Noutomi, M. Shutou, and M. Hara. 2003. Selective detection of viable bacteria using dielectrophoretic impedance measurement method. J. Electrostat. 57:157–168. [Google Scholar]
  • 8.Crane, J., and H. Pohl. 1968. A study of living and dead yeast cells using dielectrophoresis. J. Electrochem. Soc. 115:584–586. [Google Scholar]
  • 9.Huang, Y., J. M. Yang, P. J. Hopkins, S. Kassegne, M. Tirado, A. H. Forster, and H. Reese. 2003. Separation of simulants of biological warfare agents from blood by a miniaturized dielectrophoresis device. Biomed. Microdevices. 5:217–225. [Google Scholar]
  • 10.Lapizco-Encinas, B. H., B. A. Simmons, E. B. Cummings, and Y. Fintschenko. 2004. Insulator-based dielectrophoresis for the selective concentration and separation of live bacteria in water. Electrophoresis. 25:1695–1704. [DOI] [PubMed] [Google Scholar]
  • 11.Hu, X., W. M. Arnold, and U. Zimmermann. 1990. Alterations in the electrical properties of T and B lymphocyte membrane induced by mitogenic stimulation: activation monitored by electro-rotation of single cells. Biochim. Biophys. Acta. 1021:191–200. [DOI] [PubMed] [Google Scholar]
  • 12.Becker, F. F., X.-B. Wang, Y. Huang, R. Pethig, J. Vykoukal, and P. R. C. Gascoyne. 1995. Separation of human breast cancer cells from blood by differential dielectric affinity. Proc. Natl. Acad. Sci. USA. 92:860–864. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Huang, Y., X. B. Wang, R. Holzel, F. F. Becker, and P. R. C. Gascoyne. 1995. Electrorotational studies of the cytoplasmic dielectric properties of Friend murine erytholeukaemia cells. Phys. Med. Biol. 40:1789–1806. [DOI] [PubMed] [Google Scholar]
  • 14.Li, H., and R. Bashir. 2002. Dielectrophoretic separation and manipulation of live and heat-treated cells of Listeria on microfabricated devices with interdigitated electrodes. Sens. Act. B. 86:215–221. [Google Scholar]
  • 15.Archer, S., H. Morgan, and F. J. Rixon. 1999. Electrorotation studies of baby hamster kidney fibroblasts infected with Herpes Simplex Virus type 1. Biophys. J. 76:2833–2842. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Johari, J., Y. Hübner, J. C. Hull, J. W. Dale, and M. P. Hughes. 2003. Dielectrophoretic assay of bacterial resistance to antibiotics. Phys. Med. Biol. 48:N193–N198. [DOI] [PubMed] [Google Scholar]
  • 17.Labeed, F. H., H. M. Coley, H. Thomas, and M. P. Hughes. 2003. Assessment of multidrug resistance reversal using dielectrophoresis and flow cytometry. Biophys. J. 85:2028–2034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Ratanachoo, K., P. R. C. Gascoyne, and M. Ruchirawat. 2002. Detection of cellular responses to toxicants by dielectrophoresis. Biochim. Biophys. Acta. 1564:449–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Zheng, L., J. P. Brody, and P. J. Burke. 2004. Electronic manipulation of DNA, proteins, and nanoparticles for potential circuit assembly. Biosens. Bioelectron. 20:606–619. [DOI] [PubMed] [Google Scholar]
  • 20.Hölzel, R., N. Calander, Z. Chiragwandi, M. Willander, and F. F. Bier. 2005. Trapping single molecules by dielectrophoresis. Phys. Rev. Lett. 95:128102. [DOI] [PubMed] [Google Scholar]
  • 21.Carmona, M., C. Balsalobre, F. J. Muñoa, M. Mouriño, Y. Jubete, F. De la Cruz, and A. Juárez. 1993. Escherichia coli hha mutants, DNA supercoiling and expression of haemolysin genes from recombinant plasmid pANN202–312. Mol. Microbiol. 9:1011–1018. [DOI] [PubMed] [Google Scholar]
  • 22.Dorman, C. J. 2004. H-NS: a universal regulator for a dynamic genome. Nat. Rev. Microbiol. 2:391–400. [DOI] [PubMed] [Google Scholar]
  • 23.Nieto, J. M., C. Madrid, A. Prenafeta, E. Miquelay, C. Balsalobre, M. Carrascal, and A. Juárez. 2000. Expression of the hemolysin operon in Escherichia coli is modulated by a nucleoid-protein complex that includes the proteins Hha and H-NS. Mol. Gen. Genet. 263:349–358. [DOI] [PubMed] [Google Scholar]
  • 24.Nieto, J. M., C. Madrid, E. Miquelay, J. L. Parra, S. Rodríguez, and A. Juárez. 2002. Evidence for direct protein-protein interaction between members of the enterobacterial Hha/YmoA and H-NS families of proteins. J. Bacteriol. 184:629–635. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Forns, N., R. C. Baños, C. Balsalobre, A. Juárez, and C. Madrid. 2005. Temperature-dependent conjugative transfer of R27: role of chromosome- and plasmid-encoded Hha and H-NS proteins. J. Bacteriol. 187:3950–3959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Jones, T. B. 1995. Electromechanics of Particles. Cambridge University Press, New York.
  • 27.Schwan, H. P. 1957. Electrical properties of tissue and cell suspension. In Advances in Biological and Medical Physics, Vol. V. J. H. Lawrence and C.A. Tobias, editors. Academic Press, New York. [DOI] [PubMed]
  • 28.Asami, K., T. Hanai, and N. Koizumi. 1980. Dielectric analysis of Escherichia coli suspensions in the light of the theory of interfacial polarization. Biophys. J. 31:215–228. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Asami, K., and T. Yonezawa. 1996. Dielectric behavior of wild-type yeast and vacuole-deficient mutant over a frequency range of 10 kHz to 10 GHz. Biophys. J. 71:2192–2200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Gimsa, J., and D. Wachner. 1999. A polarization model overcoming the geometric restrictions of the Laplace solution for spheroidal cells: obtaining new equations for field-induced forces and transmembrane potential. Biophys. J. 77:1316–1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Huang, J. P., K. W. Yu, J. Lei, and H. Sun. 2002. Spectral representation theory for dielectric behavior of nonspherical cell suspensions. Commun. Theor. Phys. 38:113–120. [Google Scholar]
  • 32.Huang, J. P., K. W. Yu, G. Q. Gu, and M. Karttunen. 2003. Electrorotation in graded colloidal suspensions. Phys. Rev. E. 67:051405. [DOI] [PubMed] [Google Scholar]
  • 33.Zheng, L., J. P. Brody, and P. J. Burke. 2004. Electronic manipulation of DNA, proteins, and nanoparticles for potential circuit assembly. Biosens. Bioelectron. 20:606–619. [DOI] [PubMed] [Google Scholar]
  • 34.Mietchen, D., T. Schnelle, T. Müller, R. Hagedorn, and G. Fuhr. 2002. Automated dielectric single cell spectroscopy—temperature dependence of electrorotation. J. Phys. D. Appl. Phys. 35:1258–1270. [Google Scholar]
  • 35.Castellarnau, M., N. Zine, J. Bausells, C. Madrid, A. Juárez, J. Samitier, and A. Errachid. 2006. Integrated microanalytical system based on electrochemical detection and cell positioning. Mater. Sci. Eng. C. 26:405–410. [Google Scholar]
  • 36.Castellarnau, M., N. Zine, J. Bausells, C. Madrid, A. Juárez, J. Samitier, and A. Errachid. 2006. Integrated cell positioning and cell-based ISFET biosensors. Sens. Act. B. In press.
  • 37.Juárez, A., M. Hartlein, and W. Goebel. 1984. Study of regulation and transport of hemolysin by using fusion of the β-galactosidase gene (lacZ) to hemolysin genes. J. Bacteriol. 160:161–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Godessart, N., F. J. Muñoa, M. Regué, and A. Juárez. 1988. Chromosomal mutations that increase the production of a plasmid-encoded hemolysin in Escherichia coli. J. Gen. Microbiol. 134:2779–2787. [DOI] [PubMed] [Google Scholar]
  • 39.Hommais, F., E. Krin, C. Laurent-Winter, O. Soutourina, A. Malpertuy, J. P. Le Caer, A. Danchin, and P. Bertin. 2001. Large-scale monitoring of pleiotropic regulation of gene expression by the prokaryotic nucleoid-associated protein, H-NS. Mol. Microbiol. 40:20–36. [DOI] [PubMed] [Google Scholar]
  • 40.Madrid, C., J. M. Nieto, S. Paytubí, F. Falconi, C. O. Gualerzi, and A. Juárez. 2002. Temperature- and H-NS-dependent regulation of a plasmid-encoded virulence operon expressing Escherichia coli hemolysin. J. Bacteriol. 184:5058–5066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Mouriño, M., C. Balsalobre, C. Madrid, J. M. Nieto, A. Prenafeta, F. J. Muñoa, and A. Juárez. 1998. Osmolarity modulates the expression of the Hha protein from Escherichia coli. FEMS Microbiol. Lett. 160:225–229. [DOI] [PubMed] [Google Scholar]
  • 42.Finlay, B. B., and G. McFadden. 2006. Anti-immunology: evasion of the host immune system by bacterial and viral pathogens. Cell. 124:767–782. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES