Skip to main content
. 1999 Apr 13;96(8):4420–4425. doi: 10.1073/pnas.96.8.4420

Figure 2.

Figure 2

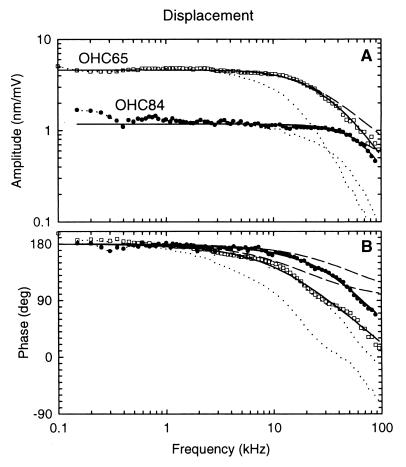
Displacement amplitude (A) and phase (B) of electrically induced length changes of two OHCs (□, OHC65; ●, OHC84) of different length measured under unloaded conditions (Fig. 1A). Displacement amplitudes (x[nm]), corrected for cell length and stimulus voltage (x[nm/mV] = x[nm]/[(1 − q)⋅q⋅USP]) (8), are given in nm/mV. Phase is referred to a depolarizing membrane potential and is positive for contraction; that is, for displacement away from the LDV. The data (symbols) are shown corrected for the measured electrical low-pass filter characteristic of the microchamber, with the OHC attached (dotted lines). Displacement data were fitted by the amplitude and phase responses of a second-order resonant system (full lines), representing the mechanical properties of the cell and extracellular fluid. Amplitude and phase were fitted simultaneously by using a software package in Microsoft Excel 7.0. The shape of the responses is described by only two free parameters: the resonant frequency, fOHC, and the quality factor, Q. Since Q was always less than 1/√2, the high-frequency limit was defined as the frequency, f3dB, at which the amplitude drops by 3 dB from its asymptotic low-frequency value; it was calculated from fOHC and Q by using the formula (f3dB/fOHC)2 = 1 − 0.5Q−2 + ((1 − 0.5Q−2)2 + 1)1/2. For some cases, a time delay (τ) was included as a free parameter in the fit function for the phase response. However, the estimated delay was in the range of the precision of our measurement equipment (<1 μs). For OHC65 (length = 83 μm; qL = 55.6 μm): fOHC = 38 kHz and Q = 0.41, giving f3dB = 18.6 kHz; τ = 0.7 μs. For OHC84 (length = 51 μm; qL = 24 μm): fOHC = 66 kHz and Q = 0.59, giving f3dB = 53.4 kHz; τ = 0.1 μs. For OHC65 and OHC84, the electrical corner frequencies of the microchamber loaded by the cell were 9.5 kHz and 23.3 kHz, respectively. The dashed lines are fits for another type of mechanical system: a first-order low-pass filter containing only stiffness and damping (corner frequency: 20 kHz for OHC65 and 54 kHz for OHC84). The near-perfect fit for a second-order resonant system and the poor fit for a first-order, low-pass filter demonstrate that the high-frequency response is determined not by damping alone, but also by inertia.