Theta oscillations by synaptic excitation in a neocortical circuit model

Abstract

Neocortical theta-band oscillatory activity is associated with cognitive tasks involving learning and memory. This oscillatory activity is proposed to originate from the synchronization of interconnected layer V intrinsic bursting (IB) neurons by recurrent excitation. To test this hypothesis, a sparsely connected spiking circuit model based on empirical data was simulated using Hodgkin–Huxley-type bursting neurons and use-dependent depressing synaptic connections. In response to a heterogeneous tonic current stimulus, the model generated coherent and robust oscillatory activity throughout the theta-band (4–12 Hz). These oscillations were not, however, self-sustaining without a driving current, and not dependent on N-methyl-D-aspartate receptor synaptic currents. At realistic connection strengths, synaptic depression was necessary to avoid instability and expanded the basin of attraction for theta oscillations by controlling the gain of recurrent excitation. These results support the hypothesis that IB neuron networks can generate robust and coherent theta-band oscillations in neocortex.

1. Introduction

A central goal in neuroscience is to understand the origin of various types of brain oscillation and their role in cognitive function (see Başar et al. 2001). Cortical theta-band oscillatory activity (4–8 Hz in humans and 4–12 Hz in rodents), for example, correlates with cognitive tasks involving attention, learning, memory, and planning (see Kahana et al. 2001). While most work has concentrated on the hippocampal origins of theta activity in rodents (see Buzsáki 2002), more recently neocortical theta activity, generated independently from hippocampus (Buzsáki 2002), has been observed during learning and memory tasks in humans (Jensen & Tesche 2002; Caplan et al. 2003; Rizzuto et al. 2003). Therefore, understanding how neocortex generates theta oscillations is essential to discovering its role in these cognitive functions.

Theta oscillations can be experimentally generated within neocortex when excitability is enhanced. First, by facilitating N-methyl-D-aspartate receptor-mediated (NMDA-R) currents field potentials with an initial large, sharp depolarization followed by 4–7 Hz oscillations are evoked or spontaneously generated in layer V of juvenile and adult isolated neocortical brain slices (Silva et al. 1991; Flint & Connors 1996; Flint et al. 1997). Second, by blocking synaptic inhibition (disinhibition) a similar field potential with theta-band oscillations (ca. 10 Hz) originating from layer V is evoked or spontaneously generated either in vivo or in vitro (Castro-Alamancos 2000; Castro-Alamancos & Rigas 2002; Bao & Wu 2003). In the first approach, however, the field potentials are lost when NMDA-R channels are pharmacologically blocked (Silva et al. 1991; Flint & Connors 1996; Flint et al. 1997), whereas in the second approach theta oscillations are lost when α-amino-3-hydroxy-5-methylisoxazole-4-propionate receptor-mediated (AMPA-R) but not when NMDA-R currents are blocked (Castro-Alamancos & Rigas 2002). This suggests that different mechanisms can generate layer V neocortical theta oscillations.

Neocortical theta oscillations are proposed to originate exclusively from the coordinated firing of interconnected excitatory networks of layer V intrinsic bursting (IB) neurons (Chagnac-Amitai & Connors 1989) for the following reasons. First, this common type of pyramidal neuron responds to a constant depolarization with 4–12 Hz rhythmic bursts of multiple action potentials (Connors et al. 1982; Chagnac-Amitai et al. 1990; Mason & Larkman 1990). Second, unlike regular spiking (RS) pyramidal cells, IB cells receive relatively little or no synaptic inhibition (Chagnac-Amitai & Connors 1989; Chagnac-Amitai et al. 1990; Nicoll et al. 1996; Schubert et al. 2001) and the synchronization of IB cells correlates with a strong synaptic excitatory signal most probably from other IB neurons (Chagnac-Amitai & Connors 1989). Third, these pyramidal cells have extensive apical and basal dendritic fields that allow them to integrate excitatory signals from all cortical layers (Schubert et al. 2001) and wide lateral intracortical axon connectivity (Markram et al. 1997) that makes them well-suited to coordinate theta activity within and between neocortical columns. Fourth, the development of IB cell-burst spiking parallels the development of NMDA-R-facilitated theta oscillations (Flint et al. 1997). Finally, recordings from individual cells participating in theta oscillations have IB characteristics (Castro-Alamancos & Rigas 2002). In contrast to this hypothesis, most experimental work stresses the importance of fast synaptic recurrent inhibition in synchronizing pyramidal cell firing (e.g. Cobb et al. 1995).

The aim of this paper was to test this hypothesis of theta wave generation by simulating a realistic spiking model of the layer V IB neuron circuit. A theoretical approach was taken because as yet the IB circuit cannot be isolated from the circuit of layer V RS-type pyramidal cells (Chagnac-Amitai et al. 1990; Mason & Larkman 1990) to test this hypothesis experimentally. Previous theoretical studies have shown under certain conditions non-depressing AMPA-R synaptic excitation can synchronize the spiking activity of realistic Hodgkin–Huxley-type models of non-frequency adapting (Hansel et al. 1995), frequency adapting (Crook et al. 1998) and chattering (high-frequency bursting) type neurons (Aoyagi et al. 2003). For neocortical IB cells, a realistic circuit model employing both non-depressing synaptic excitation and inhibition produced gamma-band oscillatory activity (40–60 Hz) rather than theta activity (Bush & Sejnowski 1996). An excitatory IB network model has been able to generate spontaneous theta oscillations but this used an unrealistic hybrid integrate-and-fire point neuron model that replaced single spikes with stereotyped bursts and did not fit synaptic parameters to empirical data on layer V IB cells (Wilken 2001). Therefore, to make the model as realistic as possible, attention was given to matching the model characteristics of synaptic transmission to that observed from the detailed study of IB–IB cell pairs in vitro including NMDA-R currents and synaptic depression (Markram et al. 1997). The simulation results show that a sparsely connected excitatory model based on these data was capable of generating robust synchronous theta oscillations provided there was a sufficient level of tonic depolarisation and synaptic depression governed recurrent excitation.

2. Material and methods

The network model was constructed to study the isolated dynamic behaviour of sparsely interconnected layer V IB neurons. For this reason the model did not include any other intrinsic or extrinsic sources of innervation to IB neurons including those within layer V such as regular spiking (RS) pyramidal cells or fast spiking (FS) inhibitory interneurons (e.g. Mason & Larkman 1990; Xiang et al. 2001). Without synaptic inhibition, which is in any case weak or absent in IB neurons (Chagnac-Amitai & Connors 1989; Chagnac-Amitai et al. 1990; Nicoll et al. 1996; Schubert et al. 2001), the model set-up equated to the experimental condition of disinhibition, where synaptic inhibition is pharmacologically blocked (Castro-Alamancos 2000; Castro-Alamancos & Rigas 2002; Bao & Wu 2003). The size of the network model was chosen to match empirical estimates from juvenile rat somatosensory cortex data that each IB neuron receives synaptic input from approximately 40 other IB neurons with a mean connection probability of 10% (see Markram et al. 1997). However, to trade off the computational cost of such a large network (i.e. 400 cells and more than 15000 connections) against cellular response variability, networks of 250 IB cells were simulated with synaptic conductance linearly scaled accordingly by factor 1.6 (400/250) to ensure the same total level of synaptic excitatory drive for fewer connections (less than 6500 connections in total) (see Wang & Buzsáki 1996). Note that the model here corresponds to the notion of spatially discrete groups of recurrently connected neurons acting as ‘local oscillators’ of theta activity suggested from experimental work (Bao & Wu 2003).

2.1 Neuron model

A previous two-compartment model with Hodgkin–Huxley (H–H)-type currents (Mainen & Sejnowski 1996; κ = 10 MΩ and ρ = 190; for further details, see electronic Appendix) was used to reproduce the intracellular firing pattern of IB neurons observed in rodent neocortex in vitro (Chagnac-Amitai et al. 1990; Mason & Larkman 1990; Silva et al. 1991; Kasper et al. 1994).

2.2 Synapse model

Excitatory postsynaptic potentials (EPSPs) between IB cells involve both AMPA and NMDA glutamate receptor components (Markram et al. 1997) and are modified by use-dependent short-term synaptic depression (Markram et al. 1997; Tsodyks & Markram 1997). To model these dynamic characteristics, a kinetic scheme used to mimic the synaptic potential time course (Destexhe et al. 1994) was modified to incorporate a phenomenological model of neocortical synaptic depression (Tsodyks & Markram 1997; Markram et al. 1998). The parameters of this synapse model were fitted to the detailed description of IB–IB EPSPs observed in juvenile rat somatosensory cortex (Markram et al. 1997). In the modified kinetic scheme, when an action potential arrives, a pulse of transmitter C released into the synaptic cleft and binding with postsynaptic receptors can be described by first-order kinetics of the fraction of receptors in the open-state, s (Destexhe et al. 1994): ds_x/dt = α_x R [C] (1 − s) − β_x s, where α_x and β_x are voltage-independent forward and backward kinetic rate constants, respectively, for synapse type x (α_AMPA = 2.0 × 10⁶M⁻¹s⁻¹, β_AMPA = 550s ^{− 1}, and α_NMDA = 2.0 × 10⁶ M⁻¹s⁻¹, β_NMDA = 25s⁻¹), and the transmitter concentration, [C] = 1 mM for fixed period of 1 ms. Synaptic transmission efficacy, R, was calculated from the fraction of synaptic ‘resource’ (e.g. transmitter vesicles) available for a single spike event, u, based on the interval between the arrival times of n and n−1 spike events, Δt_n (Tsodyks & Markram 1997; Markram et al. 1998): R_{n + 1} = 1 + (R_n − R_nu_n − 1) exp (− Δt_n/τ_R), where u_n = U = 0.59 (this was constant as no short-term facilitation effects were modelled here), and the time constant for recovery from depression, τ_R = 813 ms (Markram et al. 1998). In the dendritic compartment of the IB model neuron only, the postsynaptic currents I_syn = I_AMPA + I_NMDA are given by: $I_{\text{AMPA}}={\overline{g}}_{\text{AMPA}}{s}_{\text{AMPA}}(V-E_{\text{AMPA}})$ and $I_{\text{NMDA}}={\overline{g}}_{\text{NMDA}}{s}_{\text{NMDA}}B(V)(V-E_{\text{NMDA}})$, where ${\overline{g}}_{\text{AMPA}}=1.875 \text{nS}$ (for 400 cells), ${\overline{g}}_{\text{NMDA}}=0.625 \text{nS}$ (for 400 cells), E_AMPA = E_NMDA = 0 mV, and the voltage-dependent function to model the magnesium block of the NMDA-R B(V) = 1/(1 + exp(−0.0062V)[Mg²⁺]_o/3.57) (Jahr & Stevens 1990) with [Mg²⁺]_o = 1 mM. The time course of model unitary EPSPs of AMPA-R and combined AMPA-R and NMDA-R components had an integral difference of 54% at −30 mV and 12% at −60 mV and an amplitude of 1.3 mV at −60 mV consistent with experimental data (Markram et al. 1997). The empirical distributions of EPSP amplitude and latency were both positively skewed (see figure 4 in Markram et al. (1997)) and these were modelled using log-normal probability distributions with mean values of 1.3 mV and variance of 0.4 mV and 1.55 ms and variance of 0.8 ms, respectively. EPSP amplitude and latency values for each connection were drawn independently at random from these two distributions with a connection probability of 10% (Markram et al. 1997).

Figure 4.

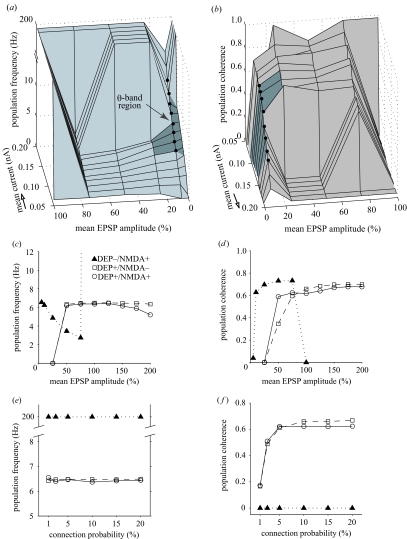
Effect of synaptic depression on theta oscillation generation. (a) Population frequency as a bivariate function of mean stimulus current and mean EPSP amplitude in IB networks without synaptic depression shows mainly delta-band (1–3 Hz) firing between 25% and 75% mean EPSP amplitude for low- and mid-range current levels, constant single spiking for 100% mean EPSP amplitude and at higher currents for all other coupling strengths except at 10%. Theta-band oscillations (see darker region) did occur at 5—25% mean EPSP amplitude but only over the full theta-band at 10% (filled circles). (b) Population coherence of (a) shows regions of high coherence corresponded mainly to delta-band oscillations with coherent theta-band oscillations only for 10% mean EPSP amplitude (filled circles) or above. Arrows show opposite orientation of plot (b) to (a). (c,d) Comparative effect of varying mean EPSP amplitude (mean coupling strength) at the same driving current (I_μ = 0.12 nA, I_σ/I_μ = 0.1). (c) Population frequency was within theta-band except less than 50% mean EPSP amplitude (0.65 mV) in networks with synaptic depression regardless of NMDA-R currents, while without synaptic depression population frequency significantly decreased as mean EPSP amplitude increased and was only within theta-band between 5% and 25%. (d) Population coherence shows that synaptic depression, with or without NMDA-R, maintained a relatively high level of coherence for theta oscillations between at least 50% and 150% mean EPSP amplitude; without synaptic depression theta oscillations were coherent only between 10% and 25%. (e, f) Comparative effect of varying connection probability (coupling density) at the same driving current (I_μ = 0.12 nA, I_σ/I_μ = 0.1). (e) Population frequency was not significantly altered by variation in connection probability. (f) Population coherence fell sharply when connection probability was reduced below 5% in networks with synaptic depression regardless of whether NMDA-R currents were blocked.

2.3 Network stimulation

To test network synchronization properties, and as in other theoretical studies of network synchronization (Wang & Buzsáki 1996; Bartos et al. 2002), a heterogeneous tonic driving current was applied to the axosomatic compartment of each model neuron. The current strength was selected from a normal probability distribution, i.e. I_app = N(I_μ, I_σ), where I_μ is the mean and I_σ the current stimulus standard deviation, with a relatively strong heterogenity (I_σ /I_μ) of 0.1 (see Wang & Buzsáki 1996; Bartos et al. 2002).

2.4 Coherence measure

To quantify the degree of synchronous spiking activity, the zero time-lag cross-correlation between a pair of cells i and j, c_ij, was calculated for a given time bin, τ, from (for details, see Wang & Buzsáki 1996):

$$c_{ij}(\tau )=\frac{\sum _{l=1}^{K}X(l)Y(l)}{\sqrt{\sum _{l=1}^{K}X(l)\sum _{l=1}^{K}Y(l)}}$$

where each spike train X and Y is represented by a binary vector such that when no spike occurs within time bin X(l), Y(l) = 0 and when one or more spikes occur X(l), Y(l) = 1, and K is the number of time bins (i.e. K = L/τ) over time-period of measurement, L = 2000 ms using τ = 0.1/f_μ (Wang & Buzsáki 1996; Bartos et al. 2002), where f_μ is the mean steady-state bursting frequency of the cell population. The population coherence measure c is the average of c_ij across all cell pairs within a network to give a measure between 0 (maximum asynchrony) and 1 (maximum synchrony) for all values of τ. This value was then corrected using the coherence value of an identical uncoupled (control) IB network.

2.5 Simulation details

To maximize the initial phase difference sub-threshold between cells, the membrane potential of each was initially set to a random value uniformly from the range −70 ± 20 mV with voltage- and calcium-dependent currents adjusted to match corresponding steady-state values. Multiple simulations with different random seeds were run to confirm results. Numerical simulations were implemented using the public-domain Neuron 5.2 environment (Hines & Carnevale 1997; software and code from http://www.neuron.yale.edu/) and run on a Pentium III PC with an integration time-step of 0.025 ms and spike transmission threshold of 0 mV.

3. Results

3.1 Theta-band population bursting

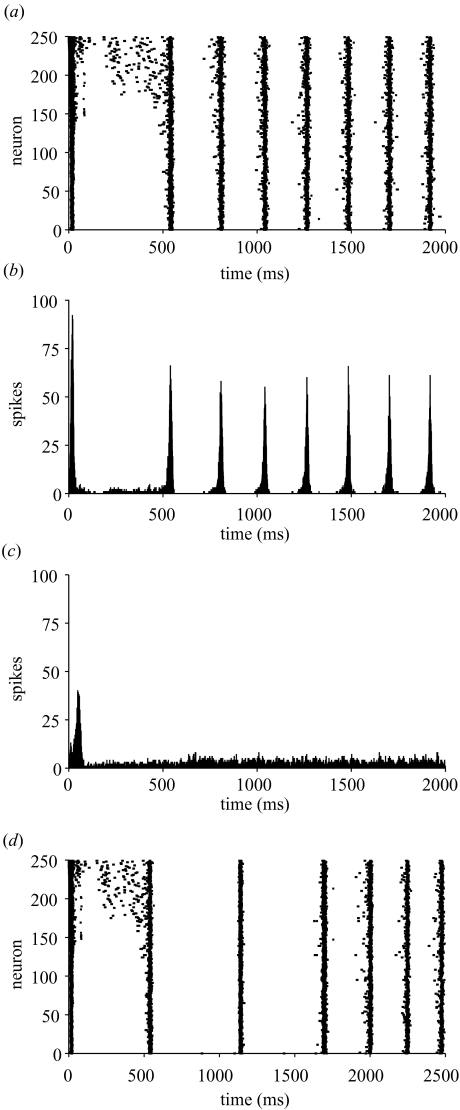
Figure 1 shows an example of the dynamic response of an IB circuit stimulated by a heterogeneous current (I_μ = 0.10 nA and I_σ/I_μ = 0.1). The raster plot shows that the initial burst of activity was not synchronous (figure 1a): the most depolarized cells (high neuron number) spiked earliest, initially in single-spike mode (see Wang & McCormick 1993), with the more hyperpolarized neurons (low neuron number) firing later with a strong burst at the start of a depolarization shift (DS), a large-amplitude (≥20 mV) and long-lasting (≥50 ms) period of depolarization (see Gutnick et al. 1982), termed a ‘DS burst’ here. The first synchronous population burst occurred at ca. 550 ms, and within a few population bursts the network had attained a constant rhythm. The corresponding post-stimulus spike histogram (figure 1b) illustrates each population burst was ca. 50 ms wide and with a strongly coherent (0.68) steady-state burst frequency f_μ = 4.65 Hz (215 ms interval), within the theta-band (4–12 Hz). Similar results were obtained with 400 IB neurons suggesting that synchronization was unaffected by scaling (data not shown). Without any connections, however, the same conditions produced only a constant rate of non-synchronized firing (ca. 5 Hz) following a small, broad initial peak artefact (figure 1c). Importantly, when the driving current was temporarily removed for 500 ms (600–1100 ms period), all circuit activity disappeared during this period but was strongly synchronized in the theta-band after the driving current was reapplied (figure 1d). This suggests IB theta synchronous activity is not simply an artefact of many cells firing but it is entrained by recurrent excitation and this activity is not self-sustaining but requires an external source of tonic excitation.

Figure 1.

Theta oscillations in a sparsely interconnected network of 250 IB neurons stimulated by a heterogeneous current. (a) Raster plot of spike times of each neuron (bottom-to-top: cell 1 initially most hyperpolarized, cell 250 initially most depolarized) shows the evolution of theta oscillations. (b) Post-stimulus spike histogram (bin size 1 ms) of coupled network in (a) shows rhythmic firing of cells at a steady-state burst frequency of 4.65 Hz (215 ms interval) within the theta-band. (c) Post-stimulus spike histogram of uncoupled (control) network shows that after a stimulus-induced burst artefact there was no rhythmic population spiking. (d) Temporary withdrawal of driving current for 500 ms (600–1100 ms period) of simulation shown in (a) eliminated population bursting but rhythmic firing recovered after the driving current was reapplied.

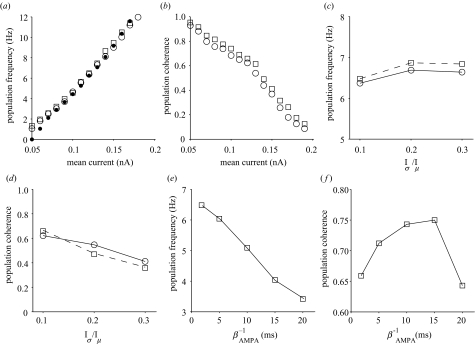
Theta oscillations in IB networks appear robust to parameter variation (Figure 2). Population frequency increased proportionately with mean driving current over the full theta-band range (4–12 Hz) and this relationship was unaffected by blocking NMDA-R synaptic currents (figure 2a). However, with or without NMDA-R currents, population coherence decreased non-uniformly with increasing mean current (figure 2b). The steady-state burst frequency of a single IB neuron over the same current range closely matched the network response (see figure 2a). IB networks with or without NMDA-R were able to maintain theta-band firing when stimulus current heterogeneity was increased (figure 2c) but this firing became significantly less coherent (figure 2d). These results suggest IB theta network oscillations are not dependent on NMDA-R synaptic currents. By contrast, population frequency was sensitive to the mean synaptic decay rate of AMPA-R conductance, which fell below 4 Hz when the decay rate was more than 15 ms (figure 2e) while coherence increased with decay rate until this point (figure 2f).

Figure 2.

Robustness of synchronous theta oscillations to parameter variation with and without NMDA-R synaptic currents. (a,b) Mean stimulus current intensity (I_μ). (a) Population frequency increased with stimulus current intensity; NMDA-R blockade had little effect. Single-cell responses (filled circles) were well matched to networks. (b) Population coherence was inversely proportional to increasing current intensity with coherence slightly improved when NMDA-R currents were blocked. (c,d) Stimulus current heterogeneity (I_σ/I_μ). (c) Population frequency increased slightly with increased current heterogeneity. (d) Population coherence quickly declined with increased current heterogeneity. (e,f) AMPA-R synaptic decay rate constant (inverse of β_AMPA). (e) Population frequency decreased below theta-band when synaptic decay rate greater than 15 ms. (f) Population coherence increased until 15 ms decay rate and then declined. Stimulus parameters (c)–(e): I_μ = 0.12 nA. Networks with NMDA-R, open circles; without NMDA-R, open squares.

3.2 Role of synaptic depression

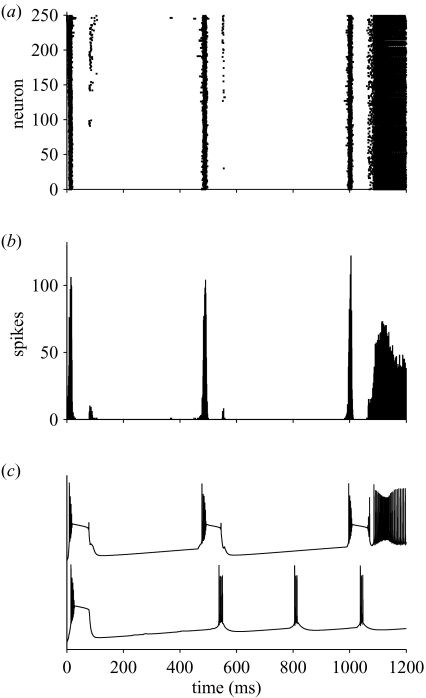
Without synaptic depression, the same network shown in figure 1 did not produce stable theta oscillations (figure 3). The raster plot shows a transition in population activity from bursting to high-frequency non-burst spiking (figure 3a). The corresponding spike histogram shows initial sharp delta-band (1–3 Hz) firing followed, after ca. 1000 ms, by a constant firing rate of 200 Hz or more (figure 3b). Without synaptic depression, an example single cell responded with an initial strong DS bursting switching, at the end of one burst, to single-spiking mode (e.g. Silva et al. 1991) compared with an initial DS burst followed by rhythmic doublet bursts when synaptic depression was present (figure 3c).

Figure 3.

Example of network activity without synaptic depression. (a) Raster plot shows initial strong, widely separated population bursts later leading to continuous spiking across the network. (b) Post-stimulus spike histogram illustrates much sharper and stronger population bursts than in figure 1b at delta (2 Hz) frequency until switching to a tonic firing of ca. 200 Hz. (c) Intracellular membrane potential of neuron no. 1 in networks with (lower trace) and without (upper trace) synaptic depression. Stimulus parameters: I_μ = 0.10 nA, I_σ/I_μ = 0.1.

To investigate whether this was a general property of IB networks without synaptic depression, the effects of varying mean coupling strength (mean EPSP amplitude), level of stimulus intensity, and coupling density (connection probability) parameters were studied (figure 4). At 100% of mean coupling strength (mean EPSP amplitude of 1.3 mV; Markram et al. 1997), networks switched from initial delta-band bursting to persistent single spiking (>200 Hz) for all mean current intensities except 0.05 nA (figure 4a,b). At 50–75% mean coupling strength, coherent delta-band (1–3 Hz) oscillations were found for low- and mid-strength currents (see figure 4a,b). However, coherent firing occurred at 4–5 Hz for 25% mean coupling strength for some mid-range currents and over the full theta-band at 10% mean coupling strength (figure 4a,b) with a similar current–frequency relationship to networks with synaptic depression at 100% coupling strength (cf. figure 2a,b). For the same driving current, coherent theta activity was maintained over a much wider range of mean coupling strengths in networks with (5–6 Hz for 50–200% coupling strength or 0.65–2.6 mV) than without synaptic depression (4–6 Hz for 10–25% coupling strength or 0.13–0.325 mV; figure 4c,d), suggesting synaptic depression expands the basin of attraction for synchronous theta activity. Varying coupling density did not significantly affect population frequency or coherence of networks without synaptic depression but networks with synaptic depression critically required a 5% or more connection probability, equivalent to 10–12 input connections per cell (figure 4e,f). Thus, only in a narrow region of parameter space, at a mean EPSP amplitude a magnitude less than found by Markram et al. (1997), can a full range of theta-band oscillations occur without synaptic depression.

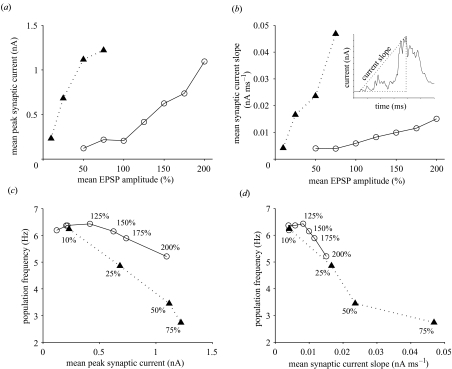
To investigate how synaptic depression could expand the basin of attraction for coherent theta oscillations, the absolute mean peak and rising slope values of synaptic recurrent excitatory current at steady-state bursting were analysed for a range of different mean coupling strengths (figure 5). Synaptic depression substantially reduced the effect of mean coupling strength on synaptic peak current (figure 5a) and rising current slope (figure 5b). For example, at 50% mean coupling strength synaptic depression reduced current slope by approximately one-fifth and peak current by approximately one order of magnitude (see figure 5a,b). For both types of network population frequency decreased as peak current and current slope increased (figure 5c,d). This paradoxical effect occurs in IB neurons because as bursts get stronger the inter-burst interval increases (see electronic Appendix). Synaptic depression generally enhanced population frequency for the same peak current (figure 5c), suggesting peak current alone does not determine population frequency in IB networks. A closer relationship existed between population frequency and current slope for networks with and without synaptic depression (figure 5d). Here the same range of current slope values for 50–200% mean coupling strength in networks with synaptic depression produced roughly the same change in population frequency as networks without synaptic depression for 10–25% mean coupling strength. This explains how, without synaptic depression, networks were able to produce theta-band oscillations for this range of mean coupling strengths only (figure 4). Thus, synaptic depression appears to expand the basin of attraction for theta oscillations in IB networks as coupling strength grows by slowing the increase of the rising slope of recurrent excitatory current.

Figure 5.

Gain control of recurrent excitation by synaptic depression. (a) Mean peak synaptic current at steady-state population bursts increased more slowly as a function of mean EPSP amplitude when synaptic depression was present. (b) Mean rising slope of synaptic current (see inset) increased more slowly as a function of mean EPSP in networks with synaptic depression. (c) Population frequency corresponding to mean peak synaptic current for different mean EPSP amplitude (values shown) illustrates that with synaptic depression population frequency generally decreased more slowly as mean peak current increased. (d) Population frequency decreased with mean current slope similarly for both types of network, but synaptic depression compressed the change in frequency with current slope up to 200% mean EPSP amplitude to correspond to the frequency change with current slope 10–25% mean EPSP amplitude in networks without synaptic depression. (Note excitatory currents are negative but to aid understanding absolute values have been used here.) Networks with synaptic depression, open circles; without synaptic depression, filled triangles.

4. Conclusions

The model results here support the hypothesis that recurrent excitation can synchronize the activity of sparsely interconnected IB neurons to generate coherent theta oscillations in neocortex (Chagnac-Amitai & Connors 1989). This suggests that neocortical theta activity associated with a range of cognitive tasks (Jensen & Tesche 2002; Caplan et al. 2003; Rizzuto et al. 2003) may originate from networks of layer V IB neurons. The model simulated here, though made more realistic than other H–H-based excitatory neocortical circuits (Hansel et al. 1995; Crook et al. 1998) by the inclusion of synaptic depression and NMDA-R currents, nevertheless simplifies normal circuit function. First, in vivo spontaneous synaptic activity alters the resting and integrative properties of cortical neurons (Paré et al. 1998), which might degrade IB synchronous firing in this model. Second, by selecting for practical reasons a neuron model with only a single dendritic compartment (Mainen & Sejnowski 1996), this ignored the influence of spatio-temporal intra-dendritic interactions of layer V neurons (Helmchen et al. 1999; Larkum et al. 1999). Finally, the sparse random-connectivity rule used here meant that the influence of lateral interactions could not be explored. Future work will address these issues and the effect of synaptic inhibition upon theta oscillation generation by the IB circuit.

To generate coherent theta oscillations in IB networks, the parameter values required (10–12 input connections per cell; >0.65 mV EPSPs; AMPA-R EPSP synaptic decay <15 ms; figures 2 and 4) are well matched to those measured in vitro (Markram et al. 1997). The fact that NMDA-R currents between interconnected IB neurons were not essential for generating synchronous theta oscillations in the model supports recent empirical work under disinhibition conditions (Castro-Alamancos & Rigas 2002). In this work, the theta oscillatory phase of the local field potential was lost when AMPA-R currents were blocked but the initial sharp depolarization phase remained (Castro-Alamancos & Rigas 2002), suggesting that facilitating NMDA-R currents provide a sufficient depolarizing envelope upon which theta oscillations can occur. Owing to the size of the model, the large, sharp depolarization phase of mass population activity observed in field potentials (e.g. Silva et al. 1991) was absent and so the model captured the oscillatory phase of firing only.

Based on available empirical evidence, the generation of robust theta activity under disinhibition in the model depended on two main conditions. First, there must be a sufficiently strong external source of tonic depolarization to produce individual neuron bursting (see figure 1). This is also a necessary condition for hippocampal CA1 bursting pyramidal circuits to generate theta oscillations in behaving rats (Harris et al. 2001). Thus, IB theta oscillations will not significantly outlast a brief period of external depolarization (e.g. 0–600 ms in figure 1d), for example, from thalamic input even though single axon EPSPs can stimulate bursting in an IB neuron in vivo (Zhu & Connors 1999). The necessity for a source of tonic depolarization to sustain synchronous theta bursting means that the IB circuit is ‘switch-like’. This steady-state depolarization might, for example, originate from layer II–III RS neurons where gamma-band firing persists after an external stimulus has been withdrawn due to long duration NMDA-R currents (Wang 1999). Layers II–III and V are strongly, and reciprocally, connected in rat neocortex (Burkhalter 1989) with layer II–III receiving thalamic input via layer IV (Lübke et al. 2000) and/or IB neurons (Markram et al. 1997). Thus, in response to a given sensory stimulus, coherent IB theta oscillations could be switched ‘on’ (facilitated) or ‘off’ (suppressed) depending on the strength of persistent activity in upper-layer RS circuits. Second, use-dependent synaptic depression was necessary at realistic mean coupling strengths to control the gain of recurrent excitation in order to synchronize individual burst firing within the theta-band. Bursting neurons are sensitive to the rising slope of a time-varying current input (Kepecs et al. 2002) and the results here indicate that synaptic depression regulates IB circuit frequency mainly by adjusting the positive slope of recurrent excitatory synaptic current (see figure 5). Owing to synaptic depression, there was a close match in the mid-range current–frequency relationship between individual IB neurons and sparsely connected IB circuit over the theta-band range (see figure 2). The quasi-linear relationship between stimulus current intensity and population burst frequency suggests that IB circuits could signal the level of mean columnar activity through its integration of excitatory signals from all cortical layers (Schubert et al. 2001). From the model, two predictions are made. First, that lowering the rate of synaptic depression will significantly reduce the basin of attraction for coherent theta oscillations in an IB circuit. Second, that under similar conditions to those used here the dynamic range of the IB circuit to stimulation should closely match that of the single IB neuron.

5. Uncited References

Aoyagi et al., 2003,Bao and Wu, 2002,Bartos et al., 2002,Bush and Sejnowski, 1996,Schubert et al., 2001