On estimating the number of species from the discovery record

Abstract

A common approach to estimating the number of species in a taxonomic or other group is to extrapolate the temporal pattern of historical species discoveries or descriptions. A formal statistical approach to this problem is described. This approach involves fitting an explicit model of the discovery record by maximum like lihood and using the fitted model to estimate the number of undiscovered species. The approach is applied to a description record of large marine animals covering the period 1828–1996. The estimated number of undiscovered species in this group is around 10 with an upper 0.95 confidence bound of around 16.

1. Introduction

A perennial problem in biology is estimating the number of species in a taxonomic or other group. (May 1988, 1990) reviewed a variety of methods. One common approach is to estimate the number of species by extrapolating to infinite time the temporal pattern of historical discoveries or descriptions (Simon 1983; Diamond 1985). Briefly, in applying this approach, the standard practice is to fit a parametric model with an asymptote to the cumulative discovery record and to estimate the total number of species from the asymptote of the fitted model. For example, in estimating the number of large (i.e. in excess of 2 m in length) marine animals, (Paxton 1998) fitted a rectangular hyperbola to the cumulative record of descriptions. The form of this model was chosen for convenience. The purpose of this paper is to place this practice on a firmer statistical footing by proposing an explicit statistical model for the discovery process and fitting this model by the method of maximum likelihood (ML).

The remainder of this paper is organized in the following way. The basic model of the discovery record is outlined in § 2. Estimation under this model is covered in § 3. In § 4, the method is applied to the description record of large marine animals compiled by (Paxton 1998), and § 5 contains some concluding remarks.

2. A model of the discovery record

We will assume that the sightings of species j, follow a non-stationary Poisson process with rate function:

$${\lambda }_j(t)={\lambda }_{j}g(t),$$ (2.1)

where λ_j is an unknown positive constant that, roughly speaking, measures the visibility of species j, and the unknown positive function, g(t), is intended to capture the trend over time in sighting skill and effort. The properties of the non-stationary Poisson process relevant here are given in Cox & Lewis (1978). Under this model, the sighting probability of species j in the interval (t, t+Δt) is approximately λ_j g(t) Δt for small Δt. It is useful to adopt the restriction g(0)=1, so that λ_j has the interpretation of the mean sighting rate of species j at t=0. A specific model for g(t) and λ_j is considered below.

Let the random variable, T_j, be the discovery time—i.e. the time of the first sighting—of species j. Under the model outlined above, the cumulative distribution function (CDF) of T_j conditional on λ_j is:

$$\text{prob}(T_j⩽t_j|{\lambda }_j)=1-\text{exp}(-{\lambda }_{j}G(t_j)),$$ (2.2)

where

$$G(t)={\displaystyle {\int }_t^{0}g(u)\text{d}u}$$ (2.3)

is the cumulative effort through time t.

We will assume that λ_j represents the realization of an exponentially distributed random variable Λ with probability density function (PDF):

$$f(\lambda )=\theta \text{exp}(-\theta \lambda ),$$ (2.4)

with unknown mean θ⁻¹. It follows that the unconditional CDF of T_j is

$$\text{prob}(T_j⩽t_j)=1-\frac{\theta }{\theta +G(t_j)},$$ (2.5)

To complete the model, we will assume that

$$g(t)=\exp (\beta t)$$ (2.6)

for unknown β. Under this complete model, the CDF of T_j is

$$\text{prob}(T_j⩽t_j)=1-\frac{\theta }{\theta +\frac{1}{\beta }(\exp (\beta t_j)-1)}=P(t_j)$$ (2.7)

and the corresponding PDF of T_j is

$$p(t_j)=\frac{\theta \text{exp}(\beta t_j)}{z{\left(\theta +\frac{1}{\beta }(\text{exp}(\beta t_j)-1)\right)}^2}.$$ (2.8)

A convenient property of the exponential form, equation (2.6) for g(t) is that the time origin t=0 need not coincide with the true beginning of the discovery period, but can be taken as any time after the beginning of this period. In that case, the relevant group consists of the species that were undiscovered as of t=0.

The model outlined above can be thought of as an extension of the Jelinski–Moranda model used in software reliability (Jelinski & Moranda 1972). Under this model, a software program contains an unknown number of errors and the times at which these errors are discovered (and repaired) are independent and identically distributed exponential random variables. In the model outlined here, the assumption that the discovery times have the same distribution is relaxed through the so-called mixing distribution, f, and allowance is made for increasing discovery effort through the function g.

3. Estimation

Suppose that over the period (0, t₀) a total of n species are discovered. Let t₁, t₂, ..., t_n be the discovery times of these species. These discovery times are assumed to have been generated independently from the model outlined in § 2 with the important proviso that they are all no later than t₀. The likelihood is defined as the joint PDF of these discovery times regarded as a function of the unknown parameters θ and β:

$$L(\theta ,\beta )={\displaystyle \prod _{j=1}^n\frac{p(t_j)}{P(t_0)},}$$ (3.1)

where p(t) and P(t) are given in equations (2.8) and (2.7), respectively. The ML estimates of θ and β are found by maximizing L(θ, β) or its logarithm.

Let $\hat{\theta }$ and $\hat{\beta }$ be the ML estimates of θ and β. There is usually little direct interest in these parameters themselves. However, by treating their estimates as correct, it is possible to construct a rough estimate of the number of undiscovered species in the group. Let m be the unknown number of undiscovered species, so that the total number of species is n+m. The number of these species that are discovered has a binomial distribution with n+m trials and success probability P(t₀). A simple estimate of m can be found by equating an estimate of the expected number of discoveries to its observed value and solving for m. This point estimate is given by

$$\widehat{m}=n\frac{1-\widehat{P}(t_0)}{\widehat{P}(t_0)},$$ (3.2)

where $\widehat{P}(t_0)$ is the estimate of P(t₀) found by replacing θ and β by their ML estimates.

It is possible to go beyond point estimation to construct an approximate confidence interval for m. Specifically, the upper bound m_u of an approximate 1−α confidence interval of the form (0, m_u) is given by the smallest value of m for which:

$${\displaystyle \sum _{i=0}^n\left(\begin{array}{c}m+n\\ i\end{array}\right)}\widehat{P}{(t_0)}^i{(1-\widehat{P}(t_0))}^{m+n-i}⩾\alpha .$$ (3.3)

By using $\widehat{P}(t_0)$ in place of P(t₀), this confidence interval ignores the variability in the estimates of θ and β and, therefore, has coverage less than 1−α.

4. Application

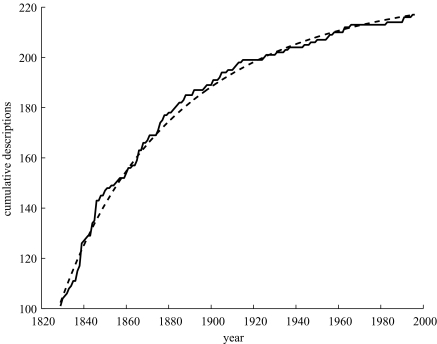
(Paxton 1998) compiled a record of the discovery times of 117 large marine animals. The first discovery in this record was made in 1829 and the last in 1995. We will take the beginning of the period of observation to be 1828 and the end to be 1996, so that t₀=169. The cumulative discovery record is shown in figure 1. This record includes 100 species discovered prior to the beginning of the observation period. We fit the model described above to this record. The ML estimates are $\hat{\theta }=52.6$ and $\hat{\beta }=0.013$. Thus, the estimated mean sighting rate at the beginning of the observation period was ${\hat{\theta }}^{-1}=0.02$ and grows thereafter at an estimated annual rate of 1.3% to reach 0.17 at the end. The estimated probability that a previously undiscovered species is discovered during the observation period is $\widehat{P}(t_0)=0.92$. The point estimate of the number, m, of undiscovered species given in equation (3.2) is $\widehat{m}=10.2$. Finally, the upper bound of the ca. 0.95 confidence interval for m based on equation (3.3) is 16.

Figure 1.

Cumulative description record of large marine animals, 1828–1996 (solid line) and fitted model (dashed line). Both curves include 100 species described prior to 1828.

The goodness of the fitted model can be graphically assessed in the following way. Under the model described in this paper, the expected cumulative number of species discovered by time t is (m+n) F(t). As in figure 1, goodness of fit can be assessed by plotting $(\widehat{m}+n)\widehat{F}(t)$ along with the cumulative discovery record. In this case, the fitted model appears to capture the behaviour of the data well.

5. Discussion

The purpose of this paper has been to describe and illustrate a formal statistical approach to estimating the number of species in a group by extrapolating the temporal pattern of historical species discoveries or descriptions. The general idea of estimating species number in this way is not entirely satisfactory, being based as it is on human activity and not on any biological considerations. Despite this, it is a common approach and therefore worth putting on a firm statistical footing. This paper appears to represent the first step in this direction.

The method described in this paper uses only the discovery record. A variety of methods for estimating species number based on the abundance of each species in a random sample of individuals have been proposed. These methods, which were reviewed by Bunge & Fitzpatrick (1993), are especially appropriate in situations in which the sampling is controlled. By contrast, the method described here is best suited for analysing historical taxonomic records that presumably were collected for quite different reasons.

Finally, the method described here could be extended in a number of ways. For example, external information about collection effort could be used either to construct the function g directly or to guide the specification of its parametric form. On the technical side, it would be possible—at the expense of additional computation—to include the effect of variability in the estimated parameters in constructing a confidence interval for m.