Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2005 Feb 4;272(1560):277–283. doi: 10.1098/rspb.2004.2969

Rates and patterns of gene duplication and loss in the human genome

James A Cotton 1,2,*, Roderic DM Page 1
PMCID: PMC1634978  PMID: 15705552

Abstract

Gene duplication has certainly played a major role in structuring vertebrate genomes but the extent and nature of the duplication events involved remains controversial. A recent study identified two major episodes of gene duplication: one episode of putative genome duplication ca. 500 Myr ago and a more recent gene-family expansion attributed to segmental or tandem duplications. We confirm this pattern using methods not reliant on molecular clocks for individual gene families. However, analysis of a simple model of the birth–death process suggests that the apparent recent episode of duplication is an artefact of the birth–death process. We show that a constant-rate birth–death model is appropriate for gene duplication data, allowing us to estimate the rate of gene duplication and loss in the vertebrate genome over the last 200 Myr (0.00115 and 0.00740 Myr−1 lineage−1, respectively). Finally, we show that increasing rates of gene loss reduce the impact of a genome-wide duplication event on the distribution of gene duplications through time.

Keywords: gene duplication, gene loss, gene families, birth–death models, 2R hypothesis

1. Introduction

Gene duplications are probably the major source of novel genetic material (Ohno 1970; Holland et al. 1994), but there has been relatively little quantitative investigation of the rates at which new genes are generated by the process of gene duplication, or of the rate at which genes are deleted from the genome, beyond the pioneering work of Lynch & Conery (2000, 2003). By contrast, there has been much interest in the pattern of gene duplications in vertebrate evolution, stemming from the ‘2R hypothesis’ that two rounds of whole-genome duplication occurred early in vertebrate evolution (Ohno 1970; Holland et al. 1994). This hypothesis has proved difficult to test, principally because most of the duplicated copies have subsequently been deleted from the genome (Skrabanek & Wolfe 1998), and because movement of genes complicates map-based approaches (Wolfe & Shields 1997). The arrival of genome-scale sequence data for vertebrates in recent years has prompted a number of investigations of gene duplications in vertebrates (e.g. Gu et al. 2002; McLysaght et al. 2002), allowing better estimates of duplication and loss rates and investigations of the pattern of gene duplication. In particular, Gu et al. (2002) presented data on the age distribution of vertebrate duplications, revealing a pattern suggestive of two major episodes of duplication: one recently, and another corresponding in time to that expected under the 2R hypothesis (although different authors have disagreed about exactly when the ‘2R’ event occurred; Skrabanek & Wolfe 1998).

Gu et al.’s original dataset consisted of 749 human gene family trees suitable for dating gene duplication events during vertebrate evolution but the only data available from this analysis are the dates of duplications across the entire dataset (X. Gu, personal communication). We have compiled a dataset (Cotton & Page 2002) showing a very similar pattern of gene duplication to that observed by Gu et al. (figure 1). These two datasets have difference strengths and weaknesses: while Gu et al. compiled a larger set of gene families (and duplications), phylogenetic trees are available for all of our gene families. Here, we use these two complimentary datasets to investigate three related questions about the interpretation of this pattern.

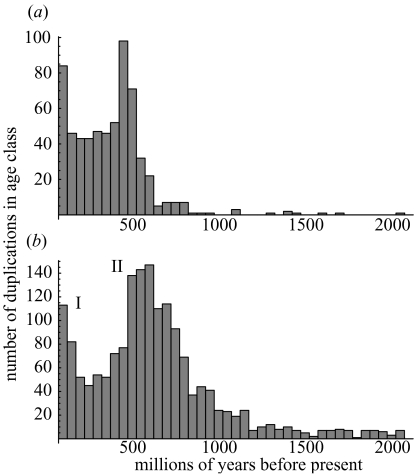
Figure 1.

Figure 1

Open in a new tab

Comparison of the results of (a) our data and (b) data from Gu et al. (2002). Figures are histograms showing the numbers of human-lineage gene duplications dated to occur at different times in vertebrate evolution in the two datasets. Roman numerals on (b) locate the two episodes of gene duplication previously identified by Gu et al.

First, we focus on whether the pattern is real, given concerns about the constancy of molecular clocks. The distributions shown in figure 1 assume a relaxed molecular clock occurring within each gene family, so that ultrametric trees (in which each leaf is the same distance from the root) can be produced, while Gu et al.’s ‘nearest neighbour’ clock assumes a relaxed clock over a smaller part of each gene family tree. There are theoretical concerns about the rate constancy of molecular clocks (Ayala 1999; Rodriguez-Trelles et al. 2002) and the accuracy of fossil calibrations (Graur & Martin 2004), and it seems likely that molecular dating studies have often overestimated the dates of evolutionary events (Conway Morris 1999). Gene duplications are constrained by speciation nodes above and below them (figure 1), giving us independent evidence about the dates of these events. More reliable dates are available for these speciation events than for gene duplications, as many genes can be used to estimate the date of a speciation event (Kumar & Hedges 1998; Heckman et al. 2001), while only the few duplicated genes can be used to estimate a duplication date (Li 1997). To test how sensitive the shape of the distribution of duplications is to molecular clock assumptions we use a method based only on the topology of gene family trees to confirm the reality of the observed pattern.

Gene duplication represents the birth of new gene lineages, while gene loss represents the death of these lineages, analogous to processes of speciation and extinction. The major results of this paper use a continuous-time model of this birth–death process (Sanderson 1994) that has previously been used to study the processes of speciation and extinction (Yule 1924; Nee et al. 1992, 1994; Kubo & Isawa 1995). The mathematical models produced to study speciation and extinction as birth–death processes (Nee et al. 1992) are equally applicable to studying gene duplication and loss, and these models suggest a different interpretation of Gu et al.’s results. Birth–death models show a characteristic shape on plots of the number of extant lineages present against time (a lineage-through-time plot; Nee et al. 1992). With no extinction and a constant gene duplication rate, these plots are exponential (and so show a straight line on a log plot). With extinction, the curves show a characteristic ‘hollowed-out exponential’ shape, increasing rapidly towards the present (or an upward curving line on a log scale; Harvey et al. 1994), as fewer older lineages persist to the present day to be observable on phylogenies of extant lineages. We compare the pattern expected under this simple model with that seen in Gu et al.’s data, allowing us to investigate how gene duplication and loss rates have varied through evolutionary time. Finally, we use a simulation-based test of model adequacy to investigate whether a constant-rate birth–death model fits Gu et al.’s data, and use this model to estimate per-lineage rates of gene duplication, which can be more easily compared with previous estimates than Gu et al.’s per-genome rate, and to present, to our knowledge, the first explicit estimates of the rate of gene loss in vertebrates.

2. Material and methods

2.1 Dates of gene duplications in the human genome

We use two different datasets of gene duplications. The larger Gu dataset of dates of gene duplications reconstructed in vertebrate gene families is from Gu et al. (2002). These dates come from 749 vertebrate gene families, and include duplications estimated to date from 4660.1 Myr ago to the present day. This older figure is certainly an overestimate, and Gu et al. truncate the distribution they show at 3500 Myr ago. For the smaller (Cotton and Page) dataset, 118 gene families that included members of a selected group of taxonomically diverse vertebrate taxa were identified from the Hovergen database. The vertebrate gene family phylogenies used in this work are available from http://darwin.zoology.gla.ac.uk/~jcotton/vertebrate_data; selection of these gene families was described in detail in Cotton & Page (2002), and the analysis is detailed below.

2.2 Reconstructing gene duplications

Alignments were generated using ClustalW (Thompson et al. 1994), with default settings, and checked by eye. Small sequence fragments that might reduce alignment quality and be difficult to place phylogenetically were removed. A maximum-likelihood estimate of the genetic distances between taxa was then found using Tree-Puzzle, v. 5.0 (Schmidt et al. 2002), using the model selected by the program, with amino acid frequencies estimated from the data and using an eight-category approximation to a gamma distribution to model rate heterogeneity between sites. These distances were then used to produce a neighbour-joining tree in PAUP, v. 4b10. Ultrametric trees were produced from these phylogenies by using the non-parametric rate smoothing method (Sanderson 1997) implemented in the R8s software package, v. 1.50, with calibration based on a date of 310 Myr ago for the divergence of mammals and reptiles. All nodes representing the relevant speciation event for this calibration point were constrained to the same age, so there were multiple calibration points in a number of gene families. Similarly, some gene families had no nodes mapping to that particular speciation, and were not included in the clock-based data. These ultrametric trees were analysed in a modified version of GeneTree (Page 1998), which produced output listing estimated dates for each node on the species tree, and for duplications mapped onto each branch on the species tree. Dates representing gene duplications that occurred along the path from the root of the species tree to humans (the evolutionary lineage of humans) were used to produce the estimated pattern of gene duplication.

2.3 Clock-independent distributions

The location of gene duplications is constrained by speciation nodes above and below them on the tree, so it is trivial to locate a set of edges on the species tree where a single duplication could have occurred (figure 2). Gene duplication events can occur at a range of different genomic scales, from a few bases to the entire genome, so duplications on different gene family trees may thus be the result of the same multiple gene duplication event. To investigate this, we clustered gene duplications from individual gene families into the minimum number of sets that may represent these larger gene duplication episodes, using a set-cover algorithm (Page & Cotton 2002). This clustering can be thought of as the distribution of duplication events if we assume that duplications of any number of genes occur with similar frequency. To examine the history of gene duplications without clustering into large episodes of duplication, we also reconstructed the most probable distribution of duplication events under the assumption that duplications occurred independently. For each branch of the species tree, the most probable number of duplications actually occurring at that location was found by summing the number of duplications that actually occurred on that branch weighted by the uncertainty in the duplication’s position. A duplication that definitely occurred at a particular location thus added one to the estimated number of duplications occurring at that location, while a duplication that could have occurred on any of three different branches added one-third to the estimate for each of the three branches. To scale these distributions, the number of gene duplication episodes from the clustering analysis and the ungrouped distribution of duplications were plotted as histograms, with a bar for each branch on the species tree, and with the x-axis scaled to represent the length of each branch using molecular date estimates (Kumar & Hedges 1998).

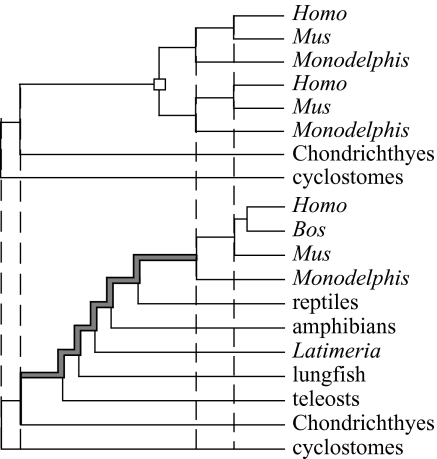
Figure 2.

Figure 2

Open in a new tab

Duplications are constrained by neighbouring speciation nodes. The duplication shown here (open rectangle) occurred before the divergence of Monodelphis and the placental mammals Mus and Homo, but after the divergence of the Chondrichthyes and the teleosts. This duplication could thus have occurred anywhere along the highlighted branch of the species tree.

2.4 Birth–death model

The models of the birth–death process used here are those of Kubo & Isawa (1995). These models are expressed in terms of numbers of lineages rather than numbers of duplications, so the data shown in figure 1 need to be converted into this form. This change is simple: we start with 749 lineages and add one lineage for each gene duplication event. A graph of these data is known as a lineage-through-time plot. The birth–death model with constant birth and death relates NT (the number of extant lineages) and Nt (the expected number of lineages at time t), by eqn 5 of Kubo & Isawa (1995):

NtNT=b-cbe(b-c)(T-t)-c,

or by their eqn 7c in the special case where birth and death rates are equal:

lnNt=lnNT-ln[1+b(T-t)].

Fitting this model to the lineage-through-time plot by the least-squares method allows estimates of the rate of lineage birth (i.e. speciation or gene duplication, b) and the rate of lineage death (i.e. extinction or gene loss, c), under the assumption that b and c remain constant. The extant number of lineages (NT) is 2488, as Gu et al.’s data start with 749 gene families and include 1739 duplications on these lineages, and T is 4660.1 for the entire dataset, and 200 for the recent duplication dataset. Model fitting and other procedures were implemented in R (code available from http://darwin.zoology.gla.ac.uk/~jcotton/RatesAndPatterns/).

2.5 Testing the fit of the constant-rate model

A parametric bootstrap procedure involved simulating 1000 datasets under a continuous-time constant-rate birth–death model with birth and death rates as estimated from the original data. Under this process, time between events is distributed as an exponential random variable, with mean 1/b+c, with the probability of an event being a birth or death being proportional to their respective rates. Simulated and observed data were compared using the deviance D=2ΣOlog(OE)) where O is the observed/simulated data and E is the expected value from the constant rate birth–death model, summed across all data points. If the deviance of the model fit to the observed data falls within the core of the distribution of the deviance of model fit to the simulated data, then the model fits the data adequately (Johnson & Omland 2004).

2.6 Non-parametric bootstrap estimates of birth–death parameters

Non-parametric bootstrapping was performed by sampling, with replacement, from the set of duplications to generate pseudoreplicate duplication histories containing the same number of duplications as the original dataset. These replicates were analysed exactly as described above for the original data, allowing us to construct confidence regions for birth and death rates.

3. Results

3.1 The pattern of gene duplications

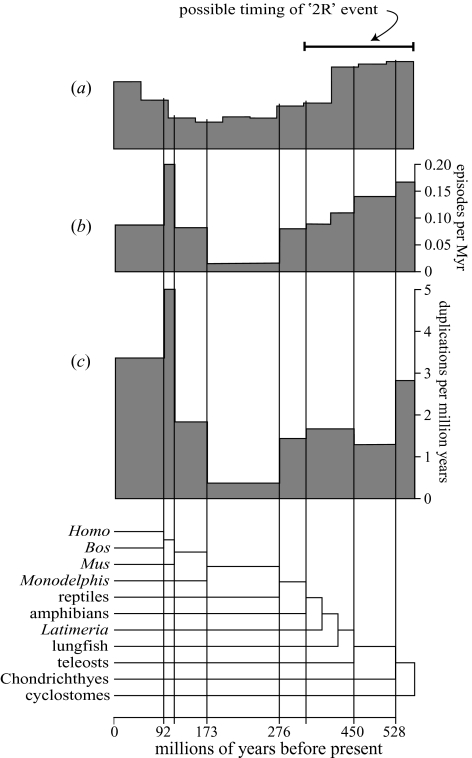
We have used topological constraints on the locations of duplications with previously estimated vertebrate speciation dates to find the distribution of duplications independent of molecular clocks for the 118 gene families in our dataset (figure 3). These distributions are similar to those in figure 1, as the deepest divergence in figure 3 dates to ca. 565 Myr ago (Kumar & Hedges 1998) and the peak to the right represents the possible ‘2R’ event (episode II, figure 1). These data seem to confirm that the pattern of duplications shown in figure 1 is not simply an artefact of the molecular clock assumption, and so demands an explanation.

Figure 3.

Figure 3

Open in a new tab

The distribution of gene duplications through human evolution independent of a molecular clock. Distribution (a) is the same distribution shown in figure 1b, truncated and with the x-axis scaled for ease of comparison.The locations of human-lineage duplications on our 118 vertebrate gene families were either: (b) clustered using the duplication clustering algorithm (Page & Cotton 2002), and the distribution of duplication episodes is shown, or (c) left unclustered, but with the ambiguity in their positions taken into account. The distributions are scaled so that branch lengths in the species tree reflected dates of cladogenesis events from Kumar & Hedges (1998). Dates were interpolated for events not included in the Kumar and Hedges study. The y-axis scale for (a) is as in figure 1b; for (b) shows the number of duplication episodes per million years; and for (c) shows the number of individual duplications per million years.

3.2 Estimation of birth and death rates

The best-fitting model for the entire data of Gu et al. suggests a duplication rate of 0.00097 Myr−1 lineage−1, and an extinction rate of 0.00048 Myr−1 lineage−1. The 95% confidence limits on these estimates, from non-parametric bootstrapping are 0.000890–0.00105 and 0.000153–0.000786, respectively (figure 5d–f). For the whole dataset, deviance was 17.971, outside the range of deviances from 1000 simulated datasets (maximum 9.08) and so giving a p-value of p < 0.001 that the observed data come from a constant-rate birth–death process, so this constant-rate model is rejected for the entire data.

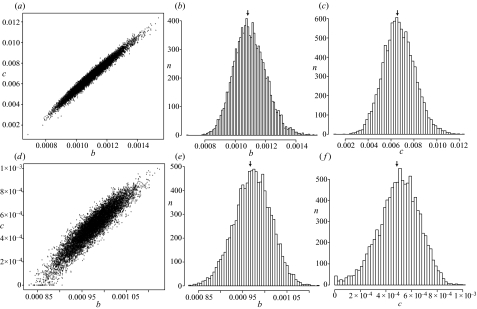
Figure 5.

Figure 5

Open in a new tab

Results of non-parametric bootstrapping on the birth and death rate estimates: (a–c) are based on parameter estimates based on the last 200 Myr of data points from the Gu et al. dataset, (d–f) are based on parameters estimated for the entire Gu et al. dataset (4660 Myr). (a) and (d) are two-dimensional confidence regions of birth rate and death rate estimates from bootstrap samples of last 200 Myr data; (b) and (e) are frequency distributions of birth rate estimates, showing the actual estimate and 95% confidence interval; and (c) and (f) are frequency distributions of death rate estimates showing the actual estimate and 95% confidence interval.

Looking at the Gu et al. data from the last 200 Myr only, we get estimated duplication rate of 0.00115 Myr−1 lineage−1 and a loss rate of 0.00740 Myr−1 lineage−1, with 95% confidence intervals from non-parametric bootstrapping of 0.000902–0.00131 and 0.00409–0.00951, respectively (figure 5a–c). D for these observed data was −0.0260, lying within the lower tail of the distribution of simulated data (range − 0.0420–0.0289), and lower than 99.3% of observations. This gives a two-tailed p-value of 0.0138<p<0.0140 that the data for the last 200 Myr come from a constant-rate birth–death process, so this model cannot be rejected at the 1% significance level for this restricted dataset.

4. Discussion

4.1 Pattern of gene duplication and loss through time

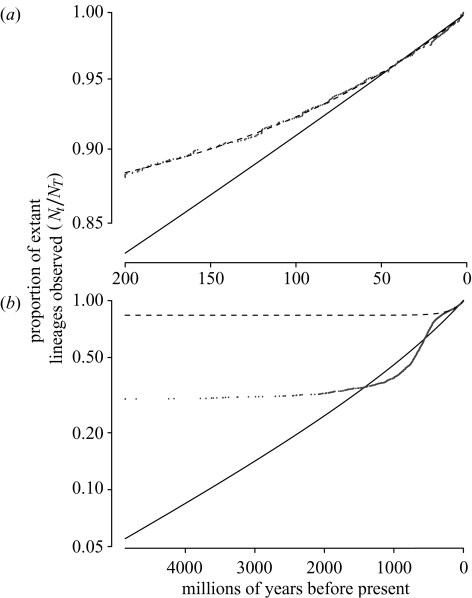
Our data show a similar pattern of duplications to that reported from Gu et al. (2002) (figure 1) but given the broadly similar methods of analysis, this is not surprising. Our topology-based method confirms the pattern of gene duplications through time suggested by these clock-based methods. Gu et al. interpreted this pattern as representing two episodes of increased gene duplication (figure 1): one of putative genome duplications occurring ca. 500 Myr ago, and a second recent increase in the rate of duplication. This is interpreted as ‘a recent gene family expansion by tandem or segmental duplications’, an event that has also been suggested elsewhere (Eichler 2001; Fortna et al. 2004). Our tests of model adequacy show that a constant rate of gene duplication and loss explains the recent pattern of gene duplications observed over the last 200 Myr, showing that Gu et al.’s episode I (figure 1) does not represent an episode of increased duplication activity. The recent sharp increase in the number of duplications follows the pattern that would be expected if rates of duplication and extinction per lineage were constant, and reflects the fact that a greater proportion of lineages from recent times are still extant in the genome (Harvey et al. 1994). By contrast, comparing the fitted model for the whole data to Gu et al.’s data (figure 4) clearly shows an increase in duplication rate ca. 500 Myr ago that cannot be explained by a constant-rate model, and which seems to represent a genuine episode of increased gene duplication (or reduced gene loss) consistent with the 2R hypothesis.

Figure 4.

Figure 4

Open in a new tab

(a,b) The constant rate birth–death model fitted using the least-squares method to the lineages-through-time plot derived from duplication ages in the Gu et al. data. The dashed line in each plot is the model fitted to the last 200 Myr, the solid line, the model fitted to the entire data. (a) Shows the results for the last 200 Myr in more detail. Note that the solid curve fits less well for older data as many of the ancient duplications will not be recorded in the data, as they will have diverged too far to be grouped in a single gene family. This will tend to make the observed curve less steep initially on the lineage-through-time plot. These points do not heavily influence the fitted curve as there are relatively few duplications this ancient in Gu et al.’s dataset.

4.2 Rates of gene duplication and loss

One limitation of this approach is that as duplicated genes diverge it will be increasingly difficult to detect similarity between them and align the genes properly. This means that any analysis based on gene family phylogenies will be less thorough in sampling older duplications than more recent events. Recent duplications, however, are more numerous, so the model (figure 4) is fitted largely to this part of the curve and is less influenced by the sparse, ancient data. Despite this, a constant-rate birth–death process can be rejected for the data taken as a whole, owing to both this sampling effect and variation in the rate of gene duplication across the data. If rates of duplication and loss have varied considerably through time, it is debatable how meaningful single estimates of these rates are. Restricting the data to the last 200 Myr, we find that a constant-rate model cannot be rejected at a 1% level, so we have used this smaller time interval for estimates of duplication and loss rates.

Our estimates of duplication and loss rates differ markedly from the only previous estimates. Lynch & Conery (2000) suggest rates of duplication of 0.0023 gene−1 Myr−1 for Drosophila, 0.0083 for Saccharomyces and 0.0208 for Caenorhabditis, and 0.0071 for human genes (Lynch & Conery 2001), while a more recent estimate (Lynch & Conery 2003) for the human rate is ca. 0.009 gene−1 Myr−1. Our estimate is thus almost an order of magnitude lower than previous estimates for human genes, and half the lowest value found by Lynch and Conery for any organism. Lynch & Conery (2001, 2003) also estimate half-lives of genes, which (under a constant rate assumption) can be converted into estimates of loss rates. The estimated half-life of 7.5 Myr for human genes (Lynch & Conery 2003) corresponds to an estimate of 0.0924 gene losses gene−1 Myr−1, again around an order of magnitude higher than our estimate. There are several problems with this earlier study, most importantly that it assumes a global molecular clock, does not test if the rates of duplication and loss are constant (Long & Thornton 2001) and may include redundant allelic sequences (Zhang et al. 2001), which would tend to inflate the rate estimates. Lynch & Conery also restrict their estimates to duplicate pairs showing less than 1% divergence at silent sites: using their estimate of 2.5 substitutions silent site−1 Byr−1, this is equivalent to discarding duplications over 4 Myr old. While this should not have a significant effect on the estimates, given that duplication and loss have occurred with an approximately constant rate over this time period, it would be expected to reduce the precision of Lynch & Conery’s estimates.

The birth–death model we use assumes that duplications and losses in each lineage are independent, and that the rates of duplication and loss stay constant throughout the tree. The effect of temporal rate variation has been investigated (Kubo & Isawa 1995): clearly, duplication and loss rates are inter-related, and particular patterns in the number of extant lineages can be explained by changes in either duplication or loss rates. There has clearly been variation in the rate of gene duplication and/or gene loss during vertebrate evolution, most notably ca. 500 Myr ago. Unfortunately, rates may also vary between lineages, for example if purifying selection makes duplicates more likely to go extinct soon after the event that gave rise to them (Walsh 1995). This violates the assumptions of the model, and may affect the accuracy of estimates from these models in a way that has not yet been investigated.

4.3 Inferring genome-scale events

Genome-scale events are difficult to observe on lineage-through-time plots if there has been a high rate of subsequent gene loss. Kubo & Isawa (1995) show that a mass speciation (equivalent to a large-scale gene duplication) event produces a discontinuity in the lineage-through-time plot as the number of lineages suddenly increases. The size of this discontinuity depends upon the extinction rate: at high extinction rates, the discontinuity will be small and may be difficult to identify against the noisy background of real data, as figure 5 shows. It is even more difficult to detect ancient events of large-scale gene loss: these are visible only as a slight ‘kink’ where the gradient of a lineage-through-time plot changes (Kubo & Isawa 1995). It is clear that good estimates of gene deletion rates will be needed to correctly interpret the peak in duplication rates observed during vertebrate evolution.

5. Conclusion

Reconstructing the pattern of gene duplications independently of molecular-clock assumptions confirms the pattern of gene duplication shown by Gu et al. and by our data. Using these data, we can use a quantitative model of the birth–death process of gene family evolution to estimate rates of gene duplication and gene loss. We show that a constant rate of gene duplication and loss fits the pattern of recent gene family evolution reasonably well, implying that, contrary to Gu et al. (2002), there has been no recent increase in duplication. Duplication and loss rates estimated here are significantly lower than previous estimates (Lynch & Conery 2000), but we confirm the high rate of loss relative to gain of new genes (figure 5a). An estimate of the rate of gene loss is crucial in interpreting the pattern of ancient gene duplication episodes. While the scale of ancient gene duplications in vertebrates is striking, it seems likely that evidence from a number of sources—from tree topology and genetic map information—will be needed to unravel the history of vertebrate genome evolution.

6. Uncited figure

Please cite figure 6

Figure 6.

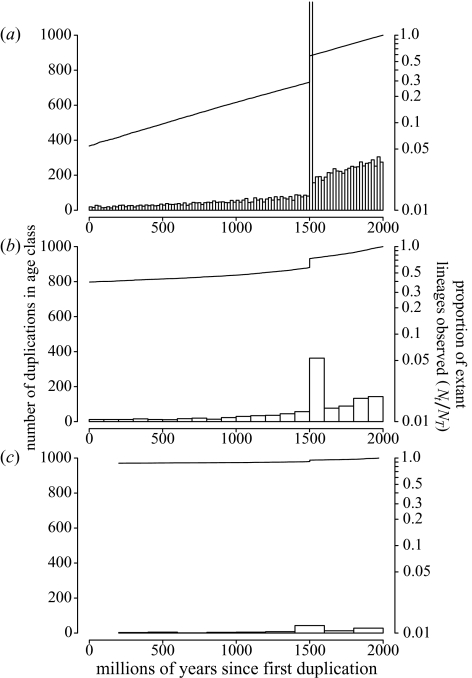
Figure 6

Open in a new tab

The results of simulations showing the effects of gene loss on the signal from an ancient genome duplication event. All three show constant rates of gene duplication (0.001097 lineage−1 Myr−1) and gene loss, with 749 lineages simulated over 2000 Myr. The loss rate is zero in (a), equal to the duplication rate in (b), and twice this value in (c). The size of the spike from the genome duplication event 500 Myr ago is much less pronounced in (b) and (c), as gene loss has erased many of the lineages duplicated in this event. In real data, there will be error in estimating duplication dates and the dispersed peak will be harder to identify against background noise. Bar charts show the frequencies of duplications through time (left-hand axis), while lines are a log lineage-thru-time plot (right-hand axis).

Acknowledgments

We thank Xun Gu and co-authors for making their data available for this study. Two anonymous reviewers made many helpful comments that greatly improved the final product. This work was supported by a NERC studentship, the Wolfson Foundation and by BBSRC grant no. 40/G18385.

References

  1. Ayala F.J. Molecular clock mirages. Bioessays. 1999;21:71–75. doi: 10.1002/(SICI)1521-1878(199901)21:1<71::AID-BIES9>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
  2. Conway Morris S. Palaeodiversifications: mass extinctions, ‘clocks’, and other worlds. Geobios. 1999;32:165–174. [Google Scholar]
  3. Cotton J.A., Page R.D.M. Going nuclear: vertebrate phylogeny and gene family evolution reconciled. Proc. R. Soc. B. 2002;269:1555–1561. doi: 10.1098/rspb.2002.2074. doi:10.1098/rspb.2002.2074 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Eichler E.E. Recent duplication, domain accretion and the dynamic mutation of the human genome. Trends Genet. 2001;17:661–669. doi: 10.1016/s0168-9525(01)02492-1. [DOI] [PubMed] [Google Scholar]
  5. Fortna A. Lineage-specific gene duplication and loss in human and great ape evolution. PLoS Biol. 2004;2:0937–0954. doi: 10.1371/journal.pbio.0020207. (and 15 others) [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Graur D., Martin W. Reading the entrails of chickens: molecular timescales of evolution and the illusion of precision. Trends Genet. 2004;20:80–86. doi: 10.1016/j.tig.2003.12.003. [DOI] [PubMed] [Google Scholar]
  7. Gu X., Wang J., Gu J. Age distribution of human gene families shows significant roles of both large- and small-scale duplications in vertebrate evolution. Nature Genet. 2002;31:205–209. doi: 10.1038/ng902. [DOI] [PubMed] [Google Scholar]
  8. Harvey P.H., May R.M., Nee S. Phylogenies without fossils. Evolution. 1994;48:523–529. doi: 10.1111/j.1558-5646.1994.tb01341.x. [DOI] [PubMed] [Google Scholar]
  9. Heckman D.S., Geiser D.M., Eidell B.R., Stauffer R.L., Kardos N.L., Hedges S.B. Molecular evidence for the early colonization of land by fungi and plants. Science. 2001;293:1129–1133. doi: 10.1126/science.1061457. [DOI] [PubMed] [Google Scholar]
  10. Holland P.W., Garcia-Fernandez J., Williams N.A., Sidow A. Gene duplications and the origins of vertebrate development. Development. 1994;(Suppl.):125–133. [PubMed] [Google Scholar]
  11. Johnson J.B., Omland K.S. Model selection in ecology and evolution. Trends Ecol. Evol. 2004;19:101–108. doi: 10.1016/j.tree.2003.10.013. [DOI] [PubMed] [Google Scholar]
  12. Kubo J., Isawa Y. Inferring the rates of branching and extinction from molecular phylogenies. Evolution. 1995;49:694–704. doi: 10.1111/j.1558-5646.1995.tb02306.x. [DOI] [PubMed] [Google Scholar]
  13. Kumar S., Hedges S.B. A molecular timescale for vertebrate evolution. Nature. 1998;392:917–920. doi: 10.1038/31927. [DOI] [PubMed] [Google Scholar]
  14. Li W.-H. Molecular evolution. Sinauer; Sunderland, MA: 1997. [Google Scholar]
  15. Long M., Thornton K. Gene duplication and evolution. Science. 2001;293:1551. doi: 10.1126/science.293.5535.1551a. [DOI] [PubMed] [Google Scholar]
  16. Lynch M., Conery J.S. Gene duplication and evolution: response. Science. 2001;293:1552–1553. [Google Scholar]
  17. Lynch M., Conery J.S. The evolutionary fate and consequences of duplicate genes. Science. 2000;290:1151–1155. doi: 10.1126/science.290.5494.1151. [DOI] [PubMed] [Google Scholar]
  18. Lynch M., Conery J.S. The evolutionary demography of duplicate genes. J. Struct. Funct. Genomics. 2003;3:35–44. [PubMed] [Google Scholar]
  19. McLysaght A., Hokamp K., Wolfe K.H. Extensive genomic duplication during early chordate evolution. Nature Genet. 2002;31:200–204. doi: 10.1038/ng884. [DOI] [PubMed] [Google Scholar]
  20. Nee S., Mooers A.Ø., Harvey P.H. Tempo and modes of evolution revealed from molecular phylogenies. Proc. Natl. Acad. Sci. USA. 1992;89:8322–8366. doi: 10.1073/pnas.89.17.8322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Nee S., Holmes E.C., May R.M., Harvey P.H. Extinction rates can be estimated from molecular phylogenies. Phil. Trans. R. Soc. B. 1994;344:77–82. doi: 10.1098/rstb.1994.0054. [DOI] [PubMed] [Google Scholar]
  22. Ohno S. Evolution by gene duplication. Springer; Berlin: 1970. [Google Scholar]
  23. Page R.D.M. GeneTree: comparing gene and species phylogenies using reconciled trees. Bioinformatics. 1998;14:819–820. doi: 10.1093/bioinformatics/14.9.819. [DOI] [PubMed] [Google Scholar]
  24. Page R.D.M., Cotton J.A. Vertebrate phylogenomics: reconciled trees and gene duplications. Pac. Symp. Biocomput. 2002:536–547. doi: 10.1142/9789812799623_0050. [DOI] [PubMed] [Google Scholar]
  25. Rodriguez-Trelles F., Tarrio R., Ayala F.J. A methodological bias toward overestimation of molecular evolutionary time scales. Proc. Natl. Acad. Sci. USA. 2002;99:8112–8115. doi: 10.1073/pnas.122231299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Sanderson M.J. Reconstructing the evolution of genes and organisms using maximum likelihood. In: Fambrough D.M., editor. Molecular evolution of physiological processes. Rockerfeller University Press; New York: 1994. pp. 13–26. [Google Scholar]
  27. Sanderson M.J. A non-parametric approach to estimating divergence times in the absence of rate constancy. Mol. Biol. Evol. 1997;14:1218–1231. [Google Scholar]
  28. Schmidt H.A., Strimmer K., Vingron M., von Haeseler A. Tree-Puzzle: maximum likelihood phylogenetic analysis using quartets and parallel computing. Bioinformatics. 2002;18:502–504. doi: 10.1093/bioinformatics/18.3.502. [DOI] [PubMed] [Google Scholar]
  29. Skrabanek L., Wolfe K.H. Eukaryotic genome duplication: where’s the evidence? Curr. Opin. Genet. Dev. 1998;8:694–700. doi: 10.1016/s0959-437x(98)80039-7. [DOI] [PubMed] [Google Scholar]
  30. Thompson J.D., Higgins D.G., Gibson T.J. ClustalW: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 1994;22:4673–4680. doi: 10.1093/nar/22.22.4673. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Walsh J.B. How often do duplicated genes evolve new functions? Genetics. 1995;139:421–428. doi: 10.1093/genetics/139.1.421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Wolfe K.H., Shields D.C. Molecular evidence for an ancient duplication of the entire yeast genome. Nature. 1997;387:708–713. [Google Scholar]
  33. Yule G.U. A mathematical theory of evolution, based on the conclusions of Dr J. C. Willis. Phil. Trans. R. Soc. A. 1924;213:21–87. [Google Scholar]
  34. Zhang L., Gaut B.S., Vision T.J. Gene duplication and evolution. Science. 2001;293:1551–1552. [PubMed] [Google Scholar]

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES