DNA as a Metrology Standard for Length and Force Measurements with Optical Tweezers

Abstract

Optical tweezers have broad applications in studies of structures and processes in molecular and cellular biophysics. Use of optical tweezers for quantitative molecular-scale measurement requires careful calibration in physical units. Here we show that DNA molecules may be used as metrology standards for force and length measurements. Analysis of DNA molecules of two specific lengths allows simultaneous determination of all essential measurement parameters. We validate this biological-calibration method experimentally and with simulated data, and show that precisions in determining length scale factor (∼0.2%), length offset (∼0.03%), force scale factor (∼2%), and compliance of the traps (∼3%) are limited only by current measurement variation, much of which arises from polydispersity of the microspheres (∼2%). We find this procedure to be simpler and more convenient than previous methods, and suggest that it provides an easily replicated standard that can insure uniformity of measurements made in different laboratories.

INTRODUCTION

The optical tweezers method, pioneered by Ashkin and co-workers, has been applied widely in biophysics research, enabling manipulation of prokaryotic and eukaryotic cells, cellular organelles, viruses, DNA, RNA, and protein molecules, and molecular motor complexes (1–9). This method allows imposition and measurement of nanometer-level displacements and picoNewton-level forces on the molecular scale. Calibration of these measurements in physical units requires accurate determination of multiple measurement parameters, and although it is possible to calculate certain parameters from physical principles in some cases (10), calibration is generally necessary. Here, we describe a simple and convenient method whereby a pair of DNA molecules may be used as reference standards for determination of all necessary measurement parameters. This approach is made possible by the fact that DNA is a linear polymer whose chemical structure is known with atomic accuracy and whose elastic force properties have been well characterized (11–14).

Conventional calibration methods usually involve multiple steps, including optical magnification calibration, microsphere centroid tracking, application of calibrated hydrodynamic flows, and statistical analysis of Brownian fluctuations (10,15,16). Although these methods are well established, none offers the convenience and precision of a universal reference standard that can be replicated by any lab. We apply this concept to metrology of optical tweezers, but note that it should also be applicable to atomic force microscopes, microneedles, and magnetic tweezers (11,17,18).

APPROACH

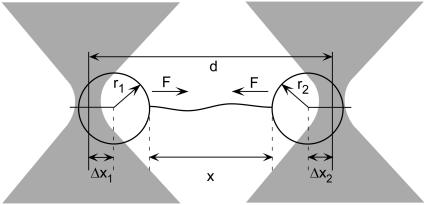
As illustrated in Fig. 1, an optically trapped microsphere subject to an external force F is displaced from its equilibrium position by a distance

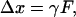(1)

where γ is the trap compliance, usually expressed in nm/pN (19). This induces deflection of the exiting laser beam, which can be measured by a position-sensing photodetector (PSD), such that the force is proportional to the measured signal by

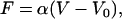(2)

where V is a measured voltage, V₀ is a voltage offset, and α is a force scale factor, usually expressed in pN/volt (19). In practice, V₀ can accurately be set to zero by measuring the detector signal under conditions with no applied force (i.e., in the absence of tethered DNA).

FIGURE 1.

Experimental geometry. The distance between the two optical traps is d, the end-to-end extension of the tethered DNA is x, the radii of the trapped microspheres are r₁ and r₂, the force on the microspheres is F, and the displacements of the microspheres from the trap centers are Δx₁ and Δx₂.

In our dual-trap system, the trap separation d is controlled using an acousto-optic deflector (AOD), creating a displacement proportional to the AOD drive frequency,

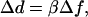(3)

where β is a scale factor, usually expressed in nm/MHz. Length measurements are thus defined by

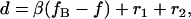(4)

where f_B is the AOD drive frequency at which the two microspheres (of radii r₁ and r₂) come into contact at F = 0; in this way, the parameter f_B specifies a length offset. Analogous parameters exist for single-trap systems that use a nanopositioning stage to generate displacements if the DNA is tethered by one end to the substrate (13), such that our method is also applicable in this case.

Complete calibration of such a system involves determination of α, β, γ, and f_B. Our approach takes advantage of the fact that the elastic behavior of double-stranded DNA is very well described by the worm-like chain (WLC) model (6,20–22). In this model, the molecular contour length per basepair, L_bp, persistence length, P, and stretch modulus, S, are physical parameters that characterize the mechanical elasticity of DNA. In this study we employ a set of high-resolution values reported in Wang et al. (13), where P = 47.4 ± 1.0 nm, S = 1008 ± 38 pN, and L_bp = 0.342 ± 0.001 nm for double-stranded DNA. We use Odijk's analytical approximation for WLC elasticity,

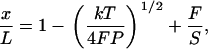(5)

where x is the end-to-end extension of the molecule, L is the contour length of the molecule, and kT is the thermal energy (∼4.14 pN-nm at room temperature) (21). We verified that this approximation agrees with the exact numerical solution (14) to within 0.1% over the range of forces being applied (4–40 pN).

When a single DNA molecule is stretched between two optically trapped microspheres, the imposed end-to-end extension is given by

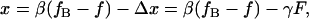(6)

where Δx = Δx₁ + Δx₂, and γ = γ₁ + γ₂ is the series compliance of the two optical traps (Fig. 1). By combining Eqs. 2, 5, and 6 we arrive at the following expression for DNA elasticity in instrument units of AOD frequency and PSD voltage,

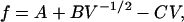(7)

where we have introduced the constants,

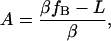(8)

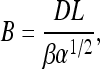(9)

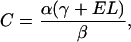(10)

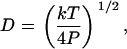(11)

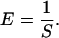(12)

Examination of Eqs. 7–10 indicates that the complete set of parameters (α, β, γ, and f_B) may be determined by measuring voltage (V) versus frequency (f) for two DNA molecules of different lengths, L₁ and L₂. The constants A_i, B_i, and C_i (for i = 1,2) may be determined by fitting these two data sets to Eq. 7. Solving the system of Eqs. 8–10 then yields the following expressions for the measurement parameters:

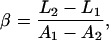(13)

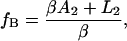(14)

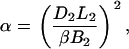(15)

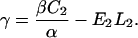(16)

We note that if β is determined independently, for example by use of a stage micrometer and video tracking of the microsphere centroid, one may calibrate the other three parameters by stretching only one length of DNA and then using Eqs. 14–16. We find it easier and sufficiently accurate to calibrate all four parameters by the single method of stretching DNA.

EXPERIMENTAL METHODS

We have demonstrated this approach using a dual-optical tweezers system built in our laboratory. In brief, our apparatus consists of a diode-pumped solid-state Nd:YAG laser (CrystaLaser, Reno, NV) split into two orthogonally polarized beams that are focused by a water-immersion microscope objective (Plan Apochromat, 1.2 NA, Olympus America, Melville, NY) to form two optical traps. One beam is steered precisely by use of an acousto-optic deflector (IntraAction, Bellwood, IL) while the other beam is fixed. The exiting beams are collected by a second objective, and the deflections of the fixed beam are measured by reimaging the back focal plane of this objective onto the face of a position-sensing detector (On-Trak Photonics, Lake Forest, CA). We verified that the response is linear (i.e., satisfies Eq. 2) up to ∼50 pN (Table 1), which covers the entire range used for calibration (4–40 pN). Linearity in this regime has been reported previously for a similar instrument configuration (19). We note that methods have also been developed to detect forces in the axial direction (23–26), and although our system is not configured for this mode of measurement, we suspect that our method of calibration would provide a simple alternative in this case.

TABLE 1.

Measurement parameters determined from the experimental data in Fig. 2

Parameter	Units	Value	Std error	% Error	Independent estimates
Length scaling (β)	nm/MHz	2141.8	3.3	0.15	2119 ± 42
Length offset (fB)	MHz	28.408	8.0e-3	0.03	28.40 ± 0.02
Force scaling (α)	pN/volt	98	2.0	2.0	102 ± 4
Compliance (γ)	nm/pN	12.28	0.40	3.3	12.20 ± 0.34

The value β was estimated by calibrated image analysis of a microsphere; f_B by estimating the contact point based on the voltage signal; γ by spectral analysis of the Brownian motion of a trapped microsphere; and α by calibrated hydrodynamic drag. A known Stokes drag was applied by flowing buffer through the chamber at a known velocity (measured by tracking microspheres released from the trap using stroboscopic illumination). N = 26 measurements were made ranging from ∼4 to 50 pN. These data were fit well by a line, with a root mean-squared deviation of 2.6 pN. The value of α was also confirmed at higher force by measuring the DNA overstretch transition.

The DNA molecules used in this study were produced by PCR using biotin- and digoxigenin-labeled primers and tethered between streptavidin and anti-digoxigenin coated microspheres (2.2-μm and 2.1-μm diameters; Spherotech, Libertyville, IL), as described previously (27). Due to the method of attachment via specific labels at each end, only intact, full-length molecules can normally be tethered. These molecules are AT-GC balanced (∼48–49% GC) and previous measurements indicate that the elasticity of such molecules typically only varies by a small amount (<2%) (27), justifying our use of the values for P, S, and L_bp reported in Wang et al. (13).

High-resolution measurements were made by changing the AOD drive frequency in 500 Hz steps and digitizing the PSD signal. Measurements were performed on 12 different 25-kbp molecules and nine different 40-kbp molecules. Multiple measurements were done to obtain averaged datasets because each molecule was tethered between a different pair of microspheres (standard deviation in radii of 2%). We note that the calibration method includes these variations and results in determination of parameters for the average microsphere. Datasets were boxcar-averaged in 10-kHz intervals and fit to Eq. 7 using the Levenberg-Marquardt least-squares algorithm (28). Precisions in determining the measurement parameters were quantified using the bootstrap method (29) to calculate the standard error, generating 100 bootstrapped datasets from each of the original 12 and nine datasets and calculating standard deviations of parameters yielded by fitting the 10,000 resultant pairings. All measurements were performed at 20.7 ± 0.5°C in a solution containing 10 mM Tris-HCl (pH 7.4), 1 mM EDTA, 100 mM NaCl, and 0.1 mg/ml BSA.

RESULTS AND DISCUSSION

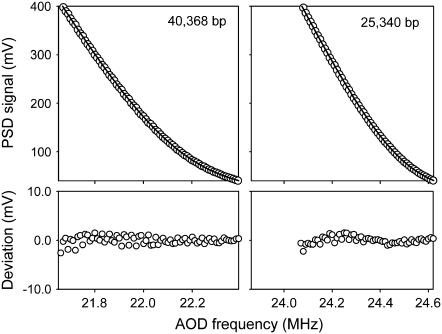
Two DNA constructs, of lengths 25,340 and 40,368 basepairs, were used as molecular reference standards and measured with a dual-optical tweezers apparatus, yielding data sets in uncalibrated instrument units of PSD voltage versus AOD drive frequency. All of the necessary measurement parameters were then obtained by fitting these data to the derived expression (Eq. 7). As shown in Fig. 2, the fits were excellent, and all four of the measurement parameters were precisely determined (Table 1). Standard errors in the length scale factor and length offset were only 0.15% and 0.03%, respectively, while the largest error (in determining compliance) was only 3.3%. A procedure for reducing this error further was also developed, as described below. The parameters determined by this method were consistent with independent estimates obtained using conventional calibration methods (Table 1).

FIGURE 2.

Averaged experimental datasets recorded for DNA molecules of the indicated lengths (points) and fits to Eq. 7 (solid lines, overlaid). Deviations from the fits are shown in the two lower plots. The fits were used to determine the measurement parameters listed in Table 1.

We further validated our technique by using simulated data (Table 2). Datasets were generated using the WLC model for the mean parameters reported in Table 1. Normally distributed noise with a standard deviation similar to that observed in the experimental measurements was added and reported uncertainties in DNA elasticity were assumed. An ensemble of such simulated datasets was then analyzed in the same manner as the experimental data. As seen in Table 2, precisions obtained with experimentally observed noise levels were in good agreement with those determined experimentally. Variations in microsphere size (standard deviation of 2%; Spherotech) account for the majority of the deviation through their effect on length offset and trap compliance (30). An ensemble of ∼60 force-extension measurements with different bead pairs confirmed this level of variation, and fits to simulated datasets showed that this variation (2.6%) could explain most of the small uncertainty in the determination of the compliance.

TABLE 2.

Dependence of the measurement parameters on measurement noise and uncertainty in the DNA parameters

Noise* (pN)	ΔP† %	ΔS %	ΔLbp %	β: Accuracy, precision (%)‡	fB: Accuracy, precision (%)	α: Accuracy, precision (%)	γ: Accuracy, precision (%)	γ': Accuracy, precision (%)§
0.05	0	0	0	8.0e-4, 0.13	4.7e-4, 0.024	0.11, 1.1	0.14, 4.6	0.051, 0.58
0.05	2	0	0	3.8e-3, 0.13	2.7e-4, 0.024	2.0, 1.1	0.063, 4.6	0.082, 0.58
0.05	0	4	0	7.8e-3, 0.13	3.2e-4, 0.024	0.13, 1.1	4.0, 4.6	3.8, 0.62
0.05	0	0	0.4	0.39, 0.13	7.4e-4, 0.024	0.16, 1.1	0.20, 4.6	0.056, 0.57
0.05	2	4	0.4	0.40, 0.13	4.7e-4, 0.024	2.0, 1.1	4.2, 4.5	3.7, 0.61
0.1	0	0	0	0.016, 0.26	2.2e-4, 0.048	0.63, 2.1	0.16, 9.2	0.13, 1.2
0.1	4	0	0	0.016, 0.27	1.9e-4, 0.048	4.0, 2.1	0.24, 9.2	0.60, 1.1
0.1	0	8	0	0.016, 0.26	7.3e-4, 0.048	0.59, 2.1	7.9, 9.0	7.9, 1.3
0.1	0	0	0.8	0.78, 0.26	9.6e-4, 0.048	0.67, 2.1	0.47, 9.2	0.67, 1.1
0.1	4	8	0.8	0.80, 0.26	7.2e-4, 0.047	4.7, 2.2	8.2, 9.0	8.2, 1.2

^*Noise standard deviations were chosen to approximate the noise level in the data in Fig. 2 (∼0.05 pN, first five rows of this table) or twice that noise level (last five rows of this table).

^†DNA parameter uncertainties were chosen to equal the reported uncertainties in Wang et al. (13) (first five rows of the table) or twice those uncertainties (last five rows of the table).

^‡Accuracy was quantified as percentage of deviation from actual value and precision as standard deviation in percentage.

^§Refined determinations of γ obtained by fixing β, f_B, and α and reanalyzing additional data sets with one-parameter fits for γ.

The very high precision in determining β and f_B derives from the fact that L₁, L₂, and f are known with high certainty. We also found by using simulated datasets that the precision in determining γ could be refined by fixing the three other measurement parameters (which could be determined more accurately) and performing a one-parameter fit to additional datasets (Table 2) or, better yet, by use of special, high uniformity microspheres (such as are available from NIST). The accuracy is limited minimally by present uncertainties in the DNA parameters. Further reductions in uncertainties of these parameters are expected as an outcome of advances in instrumentation (31).

DNA as a molecular metrology standard

Scientific measurements must ultimately be defined by comparison to standards, which is a primary concern of the field known as metrology (32). With growing interest in the study of nanoscale structures in the physical and biological sciences comes an increasing need for precise, accurate, and readily applicable standards that will insure uniformity of measurements across different laboratories.

The proposed use of DNA as a metrology standard holds interesting conceptual advantages. Its advantage as a nanoscale standard comes from its intrinsic “sameness”: a given DNA sequence has specific physical properties that are exactly the same from molecule to molecule. Furthermore, its length can be precisely controlled in incremental units of a single basepair (∼0.34 nm). Specific DNA molecules can also be replicated exactly in any laboratory by use of standard techniques in molecular biology (33).

It is important to note that the physical properties of DNA vary with temperature and solution conditions (34), so these conditions need to be controlled to obtain highly accurate results. An investigation of the ultimate limits of precision with which DNA could be employed as a standard is beyond the scope of our current study. Rather, we have demonstrated as a proof of principle a method by which DNA may be used as a physical standard for calibrating length and force measurements. Our method permitted us to determine all four necessary instrument calibration parameters with sufficient precision for most applications in biophysics and in a manner that required only a single type of measurement.