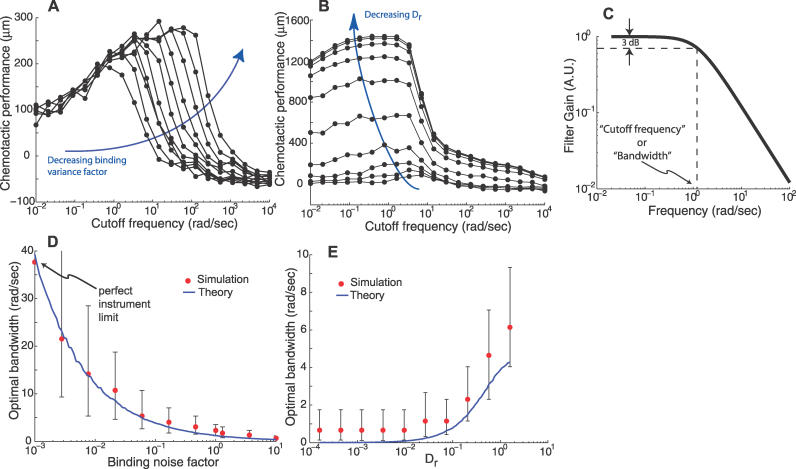
Figure 4. Noise and Rotational Diffusion Effects on Chemotaxis and the Optimal Filter.

(A) The effect of the measurement noise on the optimal cutoff frequency for chemotactic performance was studied by varying the measurement noise (by multiplying the binding variance by a factor) by several orders of magnitude and determining, as in Figure 3B, the optimal cutoff frequency. All cases showed a biphasic response. Decreasing the binding noise level results in higher optimal chemotactic cutoff frequencies and improved chemotaxis.

(B) Similarly, the effect of rotational diffusion on chemotactic performance was studied by varying the diffusion coefficient by several orders of magnitude. Decreasing rotational diffusion increases the chemotactic efficiency, but decreases the optimal cutoff frequency.

(C) The optimal filter for chemoattractant estimation was computed and its frequency-dependent magnitude plotted for a specific combination of model parameters. Its shape can be approximated by a first-order filter where the cutoff frequency is the frequency at which the gain is 0.707 (−3dB point) that of the zero frequency gain.

(D,E) The noise and rotational diffusion dependence of the optimal cutoff frequencies for chemotaxis obtained in A and B was compared with the optimal cutoff frequencies for chemoattractant estimation predicted by the optimal filter theory. The vertical bars indicate cutoff frequencies that yield chemotactic performances of 95%–100% of the maximum of the Rayleigh curve fitting (see Figure 3B). Simulation and optimal filter parameter values were as in Figure 3.