FIG. 3.
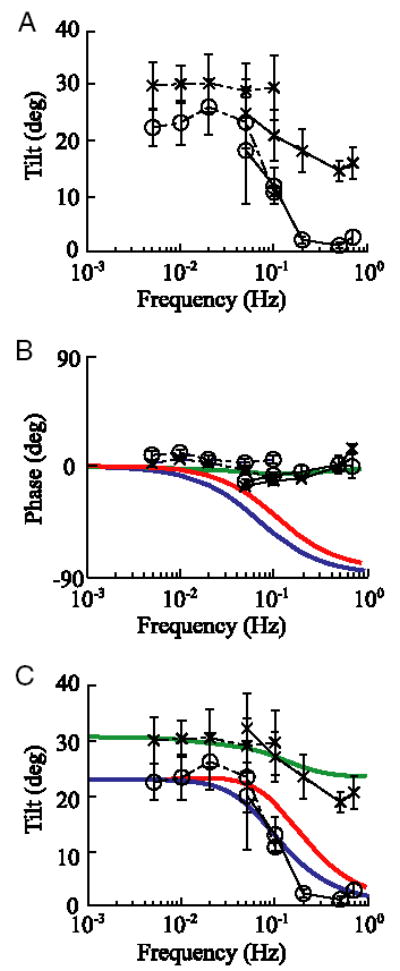
Average somatosensory tilt responses (amplitude and phase) as a function of frequency during the translation (○, n = 6 subjects) and tilt (×, n = 8 subjects) paradigms. Error bars represent SE. A: mean tilt amplitude was calculated by computing the vector average across subjects. B: mean phase was calculated by normalizing the data from each subject to have gain of 1 before performing a vector average, from which phase was calculated φ = tan−1(As/Ac). As and Ac are the mean sine and cosine components, respectively. The normalization process was performed so that the phase of responses from subjects with smaller tilt indications (e.g., 10–15°) would have the same influence on the average phase data as the phase from subjects with larger tilt indications (e.g., 30–40°). C: because previous studies have shown that continuous tilt measures underestimate tilt (Merfeld et al. 2001), we rescaled the continuous data (—) to match the amplitude of the discrete task data (···) at overlapping frequencies (0.05 and 0.1 Hz). To accomplish this, we calculated the average ratio of the mean discrete tilt indications divided by the mean continuous tilt indications at overlapping frequencies and used this ratio of 1.09 and 1.29 for each translation and tilt trial, respectively, as a scaling factor to multiply all continuous tilt settings. A first order low-pass filter (blue) was fit to the amplitude of the tilt data during the translation paradigm. A cut-off frequency of 0.07 Hz provided the best fit to the amplitude data. Internal model predictions of the phase (B) and amplitude (C) of the tilt response during tilt (green) and translation (red) paradigms are also shown. To provide a direct comparison between the tilt data and model predictions, the modeled nondimensional tilt gain (the ratio of peak estimated interaural gravitational force divided by the peak interaural gravito-inertial force) was scaled to best match the data with the scaling factor of 30.7 and 24.0° for translation and tilt paradigms, respectively.
